基于鲸鱼优化和批量规范化卷积神经网络的振动信号去噪

谭继勇,罗 俊,谢江涛,秦玉玺,汪友明

(1.西南电子设备研究所,四川 成都 610036;2.西安邮电大学自动化学院,陕西 西安 710121)

0 引言

振动信号处理及分析是旋转机械健康管理的常用方法,主要从振动信号中提取旋转机械运行状态的特征信息。而旋转机械在复杂的工作环境中易受到摩擦、冲击等影响,导致采集的振动信号含有大量的噪声,对后续的健康管理产生了负面影响[1-2]。因此,对采集到的原始振动信号进行去噪具有重要意义。传统的去噪方法包括小波阈值去噪[3]、经验模态分解(empirical mode decomposition,EMD)[4]和奇异值分解[5]等。但这些方法仍存在一些待解决的问题,如需要人工选择和经验调整参数来进行去噪,且与工程师的经验密切相关。

近年来,深度学习已在图像去噪[6]、自然语言处理[7]和故障诊断[8]等各个领域得到了快速发展。作为深度学习中的一种典型算法,卷积神经网络(convolutional neural network,CNN)在信号去噪和图像去噪领域得到了广泛的应用。Jain等[9]采用CNN学习从低质量图像到纯净图像的端到端的非线性映射,以去除图像中的噪声。Han等[10]提出了一种基于非局部全卷积神经网络的振动信号去噪方法。邢玉龙等[11]提出了一种基于全卷积神经网络的信号去噪方法,以消除机车信号中的噪声。CNN可以提取图像或信号中的局部特征,以完成良好的去噪效果,但其初始权值的选取随机性较大,导致网络学习速度缓慢、易陷入局部最优等问题。

元启发式算法在优化网络架构和训练参数方面有很大的潜力,包括粒子群、遗传、差分进化、蚁群、灰狼和模拟退火等[12]。然而,这些算法容易陷入局部最优解,参数设置较多,难以高效搜索最优解。鲸鱼优化算法[13]具有强大的全局搜索能力,算法参数较少,从而避免网络陷入局部最优解。因此,本文提出一种基于鲸鱼优化算法(whale optimization algorithm,WO)和批量规范化卷积神经网络(batch normalization convolutional neural network,BN-CNN)的振动信号去噪方法。

1 BN-CNN网络

BN-CNN引入了残差学习的思想[14],用于学习含噪信号中的噪声特征。将含噪振动信号的幅度谱和噪声信号的时域波形分别作为训练特征和训练目标进行训练和测试,通过作差得到去噪的振动信号。BN-CNN网络的结构框架如图1所示。该网络模型首先采用卷积层和ReLU激活函数对输入信号进行特征提取。其次,输入到由卷积层、BN层和ReLU激活函数组成的并行模块中,通过不同大小的卷积核对特征进行由大到小的特征提取。最后,采用一个全连接层进行特征融合,并输出噪声信号。

图1 BN-CNN网络框架

2 基于WO-BN-CNN的振动信号去噪

2.1 鲸鱼优化算法

鲸鱼优化算法是一种基于复杂优化问题进行寻优的算法,模拟了座头鲸群体的捕猎行为。该算法可分为以下3步:

a.包围收缩。该阶段模拟鲸群识别猎物并且收缩包围圈的动作。将最靠近目标猎物的个体位置设为最优位置Xb(t),随着迭代次数增加,鲸鱼个体不断更新位置朝猎物靠近,实现收缩包围猎物。鲸鱼的位置更新公式为:

X(t+1)=Xb(t)-AD

(1)

D=|CXb(t)-X(t)|

(2)

b.螺旋捕食。在围捕猎物时,鲸鱼通过螺旋向上游动的方式向猎物移动并吐出气泡对猎物进行捕食,即在螺旋更新位置的同时对包围圈进行收缩。螺旋捕食公式为

(3)

式中:D*=|Xb(t)-X(t)|;p为[0,1]内的随机数;l为[-1,1]内的随机数;β为螺旋线状常数。

c.搜索猎物。当|A|>1时,鲸鱼随机选择1个领导个体,以此进行全局搜索。搜索公式为:

X(t+1)=Xrand(t)-AD

(4)

D=|CXrand(t)-Xi(t)|

(5)

式中:Xrand为随机选择的鲸鱼位置向量。

2.2 基于鲸鱼优化算法的BN-CNN网络

为了解决BN-CNN网络在随机调节网络参数的随机性,易陷入局部最优的问题,采用WO进行优化BN-CNN网络,如图2所示。将BN-CNN中的权值参数作为算法中的鲸鱼个体位置,网络在训练模型时的损失函数作为WO算法的目标函数,通过寻找损失函数最小的鲸鱼位置得到最优的BN-CNN神经网络权重参数。具体步骤如下:

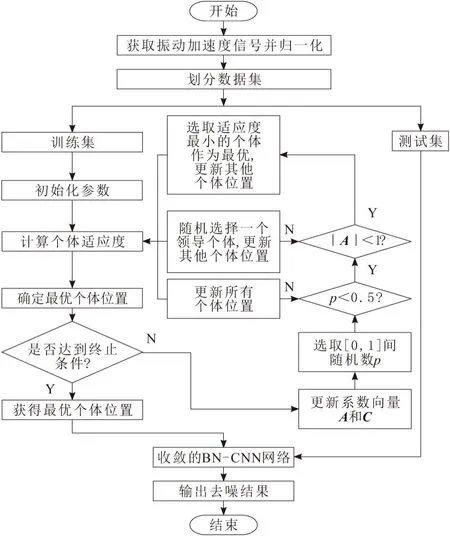
图2 鲸鱼算法优化神经网络

a.编码。向量编码是指将神经网络中的每个向量都作为优化算法中的个体位置进行编码,将BN-CNN神经网络中卷积层的权值参数作为WO算法中的鲸鱼个体位置,具体表示方式为

Uij=[ω14,ω15,ω16,ωij,…,ω24,ω25,ω26,…]

(6)

b.目标函数。鲸鱼优化算法在求解最优解时主要通过目标函数来保留或者淘汰个体。在WO优化BN-CNN神经网络时,选择合适的目标函数可以提高算法的收敛速度, 扩大搜索范围以获得全局最优解。鲸鱼在捕食行为过程中会使得损失函数达到最小值,目标函数由均方误差损失和平均绝对误差组成,计算公式为

(7)

c.鲸鱼算法优化BN-CNN神经网络。具体流程如下:

①选定训练集,从样本集中分别随机寻找样本作为训练集。

②将BN-CNN神经网络中卷积层的权值参数作为WO算法中的鲸鱼个体位置进行编码。

③初始化BN-CNN神经网络权值参数。将网络中各阈值、权值初始化为接近0的随机数。

④初始化WO算法参数,即鲸鱼种群的规模大小、最大迭代次数以及鲸鱼种群位置。

⑤计算每一头鲸鱼的适应度值。

⑥对鲸鱼适应度值的大小进行排序,选取W个作为初始种群。

⑦根据W个个体的适应度值的大小,将适应度值最小的个体位置作为最优位置。

⑧判断是否达到终止条件,若满足则获得最优个体位置,即BN-CNN的最优权值参数,进入下一步;否则,更新个体位置,返回⑤。当概率p≥0.5时,更新其他个体位置。当p<0.5且|A|≥1时,随机选择1个领导个体,更新其他个体位置;当p<0.5且|A|<1时,选择适应度最小的个体作为最优,更新其他个体位置;

⑨将最优的权值参数重构BN-CNN,并用训练集训练获得收敛的BN-CNN网络。

3 实验和结果分析

3.1 数据集与参数设置

实验采用美国凯斯西储大学的滚动轴承振动信号数据集。实验台由1台1.5 kW(2HP)电机、1个扭矩传感器和1个安装在驱动端轴承座上的功率计组成,如图3所示,加速度传感器用于采集滚动轴承的振动信号数据。被采集的轴承存在内圈故障、外圈故障和滚珠故障等3种缺陷位置,损伤直径分别为0.18 mm、0.36 mm和0.54 mm,共9种故障状态。本实验所用的10种状态的振动信号时域波形如图4所示。采用快速傅里叶变换获取振动信号的频谱图,如图5所示。

图3 西储大学滚动轴承数据采集实验台

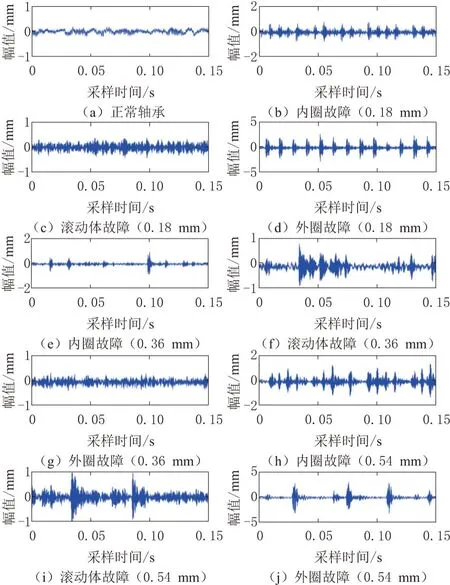
图4 滚动轴承振动信号的时域波形

图5 滚动轴承振动信号的频谱图

由于数据集的样本少,并存在不均衡问题,采用单个数据重复加噪的方式增加样本数量。在生成训练数据集时,分别将9个不同噪声水平的高斯白噪声(噪声水平为50%～150%)与原始振动加速度信号相叠加构成含噪信号,并与原始振动信号组合成对。采用长度为2 000的窗口以50%重叠率扫描所有训练数据,形成训练数据集。实验采用含噪振动信号的幅度谱作为训练特征,含噪振动信号(噪声水平为50%～150%)频谱如图6所示。

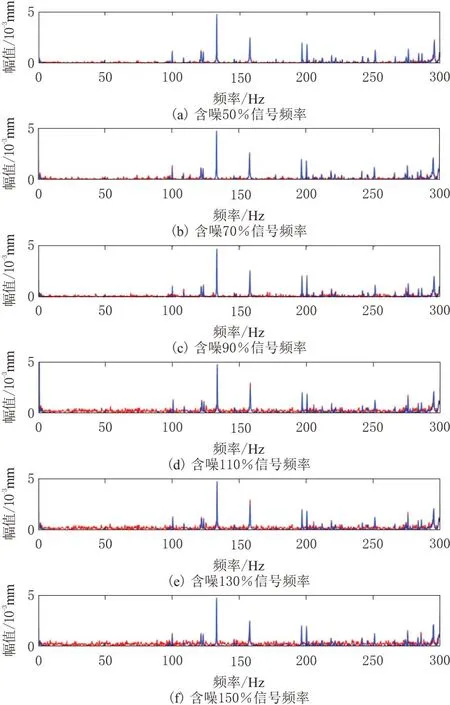
图6 含噪振动信号(噪声水平为50%～150%)频谱图

本实验所用计算机处理器为Intel(R)Core(TM) i5-9400F CPU@2.90 GHz,显卡为NVIDIA GeForce GTX 1080,内存为16 GB。神经网络采用开源的Tensorflow1.4.0模块搭建,软件编程环境为Python3.6。网络模型中初始学习率设置为0.001,epoch大小设置为100次,batch大小为16,WO算法最大迭代次数为300。BN-CNN网络模型的参数配置如表1所示。为了评估信号去噪效果的优劣,采用信噪比(signal to noise ratio,SNR)、均方误差(mean squared error,MSE)和平均绝对误差(mean absolute error,MAE)对网络模型去噪后的效果进行评价,公式如下:

(8)

表1 网络模型的参数配置

(9)

(10)

TSNR值越大,TMSE和TMAE越小,代表去噪性能越好。

3.2 实验结果与分析

对正常轴承、内圈故障(损伤直径为0.18 mm)、滚动体故障(损伤直径为0.18 mm)、外圈故障(损伤直径为0.18 mm)4种状态下的轴承振动信号进行去噪,含噪信号以及采用所提方法去噪后信号的信噪比变化如图7所示。可以看出,去噪信号的信噪比都大于含噪信号的信噪比,表明所提方法可以有效地提高信号的信噪比,减少噪声成分。

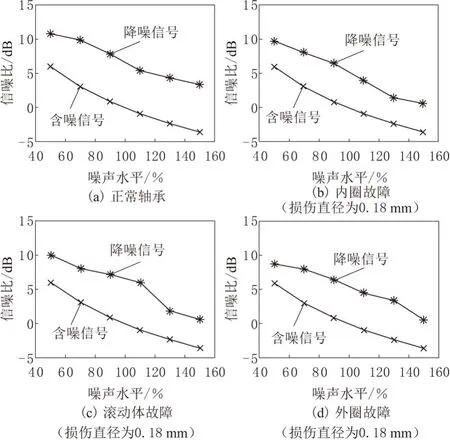
图7 含噪声信号和去噪信号的信噪比

为了验证所提模型的去噪能力,将其与小波阈值去噪、EMD去噪、CNN、PSO-BN-CNN进行对比,如表2所示。结果表明,与小波阈值去噪和EMD去噪方法相比,采用CNN进行去噪可以有效地提高信号质量和信噪比。与基于时域特征的BN-CNN模型相比,基于幅度谱的BN-CNN模型的性能指标得到较大提升。与CNN与PSO-BN-CNN方法相比,本文所提WO-BN-CNN方法在不同强度的高斯白噪声下不仅提高了SNR值,并且MAE与MSE更低,表明引入残差学习和BN层可以更容易学习到噪声特征,使网络收敛更快,采用时频域特征可以更好地拟合含噪信号幅度谱与噪声之间的关系,有效验证了本文模型的去噪能力。

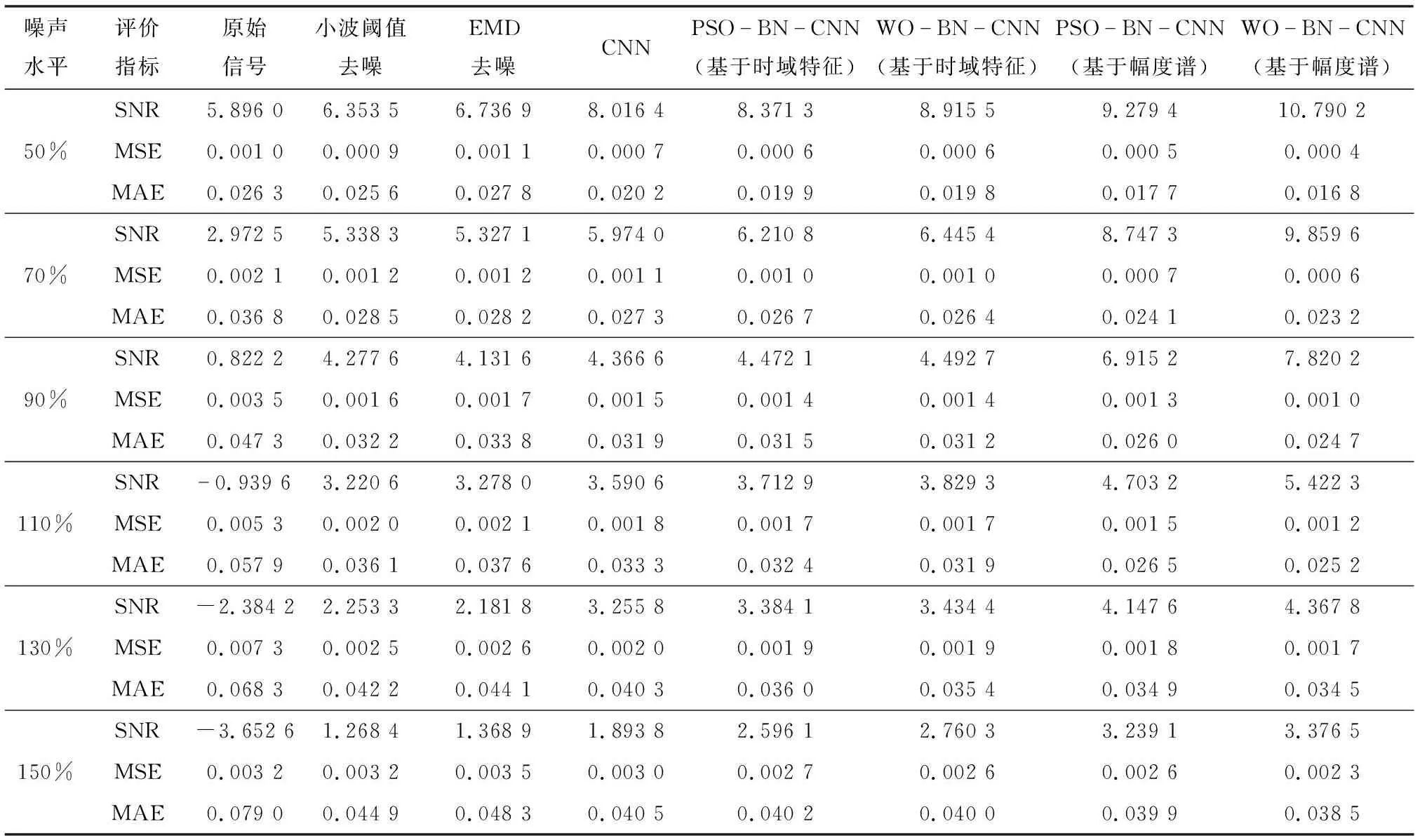
表2 不同方法的去噪性能比较

4 结束语

针对传统卷积神经网络易陷入局部最优,难以从含噪振动信号中提取纯净信号的问题,本文提出了一种基于WO-BN-CNN的振动信号去噪方法。分别采用含噪振动信号的幅度谱和噪声信号的时域波形作为训练特征和训练目标,充分利用了振动信号在时频域上的分布情况。将BN层加入到CNN之后进行归一化,并结合WO算法用于优化BN-CNN的权值参数。通过引入残差学习的思想,学习含噪信号中的噪声特征,实现振动信号去噪。实验结果表明,相较于对比的去噪方法,WO-BN-CNN方法具有更高的信噪比、更低的MSE和MAE,提升了去噪效果。