基于FCS-MPC的TNPC-UPQC补偿策略研究

蔡修闻,赵 涛,张铭洲,李桂璞

(南京工程学院,江苏 南京 211167)

0 引言

随着新能源产业发展,社会各行业对电能需求量的不断增多,电力电子器件的广泛应用,大量敏感负载接入电网,都对电能质量提出了更高的要求[1-4]。1996年,Akagi[5]提出了统一电能质量调节器(unified power quality conditioner,UPQC),其由串联有源滤波器与并联有源滤波器组合而成,可根据电网的实时状况对电能质量进行综合补偿,因此成为改进电网电能质量问题的热门研究方向[6-9]。

目前在UPQC的控制策略研究方面,线性控制方法占主要地位[10-11],文献[12]采用了PI控制;文献[13]将神经网络控制系统应用于PI控制器中;文献[14]中以MMC-UPQC并联侧电流进行了PID补偿控制。但传统线性算法具有烦琐的参数调节问题[10,11,15],因此如何进一步降低UPQC控制算法的复杂度尤为重要。而FCS-MPC因其具有的滚动优化和反馈校正功能,能够提高预测精度、增强系统鲁棒性[16],且其控制思路简单、不用额外增加其他控制模块,使得设计难度大大降低,近年来被广泛运用于变流器、电机控制领域中。文献[17]提出了一种使用FCS-MPC的三电平并网逆变器兼谐波治理系统,在利用太阳能资源的同时又能提高电能质量;文献[18]提出了三电平逆变器、MPC与状态观测器相结合的复合控制方案,并将该方法应用于电机驱动系统。文献[15]和文献[19]提出了一种基于FCS-MPC的UPQC电能质量扰动补偿策略,相对于传统PI闭环控制系统,有效降低了参数调试的烦琐性。

UPQC串联侧与并联侧的变流器目前有两电平与三电平拓扑结构,相比传统的两电平结构,三电平结构具有输出电压高、稳定性强和谐波含量少等优势[20-21]。三电平变流器拓扑结构有中点箝位式变流器(neutral point clamped,NPC)和T型中点箝位(T-type neutral point clamped,TNPC)型变流器2种。

与NPC型变流器相比,TNPC型三电平结构减少了开关器件的数量,节约了系统成本,且目前关于TNPC-UPQC的研究较少。因此,本文采用了三电平变流器作为电路的主要拓扑结构与UPQC结合构成TNPC-UPQC系统,提出一种基于FCS-MPC的TNPC-UPQC的控制策略。

1 TNPC-UPQC的拓扑结构与数学建模

TNPC-UPQC的拓扑结构如图1所示,主要由采用T型三电平构成的串联变流器与并联变流器组成,串联变流器与变压器一起串联接入电网与负载之间,是系统电压补偿单元的重要组成部分,用于在电网侧电压发生暂降或者暂升故障时进行补偿。并联变流器则是电流补偿单元的重要组成部分,并联接入在靠近负载侧的位置,用于补偿负载侧出现不平衡负载和非线性负载带来的电流谐波等电能质量扰动。

图1 TNPC-UPQC的拓扑结构

图1中,usa、usb、usc为电网提供的三相交流相电压;isa、isb、isc为电网侧三相电流;Ta11～Tc14与Ta21～Tc24为串联变流器与并联变流器的各桥臂上的IGBT开关管;ua1、ub1、uc1与ua2、ub2、uc2为串联变流器与并联变流器的三相交流相电压;uca、ucb、ucc为串联变压器电网补偿电压;ufa、ufb、ufc为串联变流器侧电压;uLa、uLb、uLc为负载侧三相交流相电压;ioa1、iob1、ioc1为串联变流器输出的补偿电流;ia1、ib1、ic1与ia2、ib2、ic2分别为串联变流器与并联变流器的输出三相线电流;iLa、iLb、iLc为负载侧三相电流;L1与L2为串联变流器与并联变流器的输出电感;C1为滤波电容;C为直流侧储能电容;udc1、udc2为直流储能侧电容电压。

T型三电平变流器在工作时abc三相均可输出3种开关状态,分别用“N”、“O”、“P”表示。定义开关函数为

S=[Sa,Sb,Sc]

(1)

式中:Sa、Sb、Sc∈(-1,0,1),分别为开关状态“N”、“O”、“P”。

因此,该变流器共有27个开关状态组合,这些开关状态可以表示为空间电压矢量u1～u27,基于数值大小的不同可以将它们分为4种矢量:零矢量(Vzero)、小矢量(Vsmall)、中矢量(Vmedium)和大矢量(Vlarge)。

由图1的UPQC拓扑结构,根据基尔霍夫定律,可得到串联侧数学模型为

(2)

式中:i1αβ为流经串联侧电感的三相输出电流;ufαβ为串联变流器侧电压;u1αβ为串联变流器的三相交流相电压;io1αβ为串联普流器输出的补偿电流。

同理,可得并联侧数学模型为

(3)

式中:i2αβ为并联普流器的输出三相线电流;u2αβ为并联普流器的三相交流相电压;uLαβ为负载侧三相交流相电压。

2 基于FCS-MPC的TNPC-UPQC控制策略

2.1 FCS-MPC的基本原理

FCS-MPC以变流器离散化后的数学模型为基础,通过价值函数对开关状态进行寻优,并将最优开关状态直接输入给变流器。

其控制器方案一般分以下3个步骤:

a.建立基于控制对象的离散化数学模型,并确定输入与输出变量之间的数学关系以及所有可能会出现的开关状态S1～Sn,预测未来的系统状态量in(k+1)。

b.根据需要达到的系统预期建立价值函数。

c.滚动优化,找出最优开关状态,并将最优开关状态作用于控制系统。

2.2 电压电流补偿量检测

串联变流器电压补偿量计算环节如图2所示。

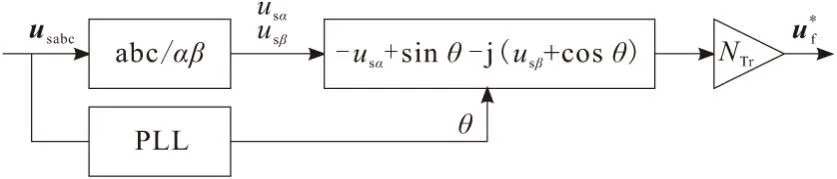
图2 电压补偿量计算环节

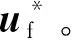
并联变流器电流补偿量计算环节如图3所示。

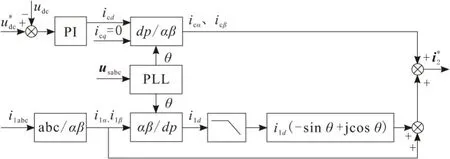
图3 电流补偿量计算环节

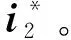
2.3 串联侧电压补偿单元控制策略

通过前向欧拉离散化式(2)可得

(4)

式中:Ts为采样周期;k∈N,记作离散时间的步长。

并联侧的数学模型建立与变换处理与串联侧相同。

直流储能侧的电容电压动态过程在离散时间域的模型可表示为

(5)

idc1(k)、idc2(k)分别为流过直流侧电容C1、C2的电流,通过引入的开关状态变量函数H1x和H2x可表示为

(6)

式中:icl为串联侧所产生的电流。

开关状态变量函数H1x和H2x定义为

(7)

根据系统预期的控制目标,建立价值函数G,如式(8)所示,通过滚动优化方式,遴选出使得G最小的电压矢量作为最优矢量,同时将其对应的开关状态输出至变流器。

G=λ1·g1+λ2·g2

(8)

式中:g1、g2为子价值函数;λ1、λ2分别为对应子价值函数的权重因子。

并联侧各子价值函数为:

(9)

(10)

在滚动优化时,变流器的27个空间电压矢量都参与遍历计算,过多计算次数会增加控制器的运算量,但对电压矢量进行过度筛选会导致并网电流质量降低。因此,本文参照文献[22]中的优化分区最优子集原则,如图4所示,根据中矢量方向可以将27个空间电压矢量分为6个六边形。设参考电压信号与大矢量“PNN”夹角为δ,由此可定义小六边形区域号M与夹角δ之间的数学关系为

图4 电压空间矢量分布

M=ceil[(δ+30°)/60°]δ∈[0,360°]

(11)

式中:ceil为返回不小于其表达式的整数的函数。

最优子集即每个六边形中包括了3个Vzero、6个Vsmall、2个Vmedium、1个Vlarge,一共12个空间电压矢量。这样划分区域的优点在于,MPC获得了利用更多Vsmall调节中点电位平衡的能力的同时,计算速度并没有降低,并且增大了权重因子λ2的选取范围,不必在对其的整定上花费大量精力。

2.4 并联侧电流补偿单元控制策略

与串联侧相同,欧拉离散化式(3)后建立价值函数G为:

(12)

(13)

i2αβ(k)

(14)

n=1,2,…,27

(15)

通过Uαβref(k)判断优化扇区后通过价值函数寻优输出最佳开关状态。

3 仿真结果与分析

在MATLAB/Simulink环境下,根据上述控制算法搭建系统模型。本文所提控制策略如图5所示。

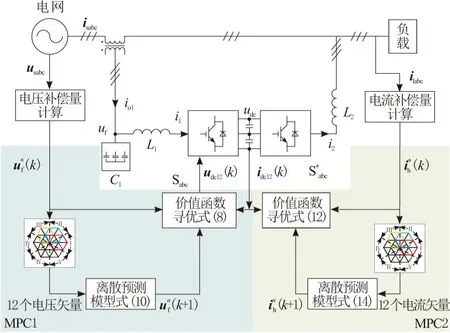
图5 控制策略

各仿真参数如表1所示。电网电压发生暂降故障时TNPC-UPQC补偿情况如图6所示,电网电压在0.1 s时发生跌落,幅值下降30%,0.15 s时恢复正常,在UPQC补偿作用下,负载侧三相电压波型在故障过程中能够保持幅值稳定与对称性。

表1 系统主要仿真参数

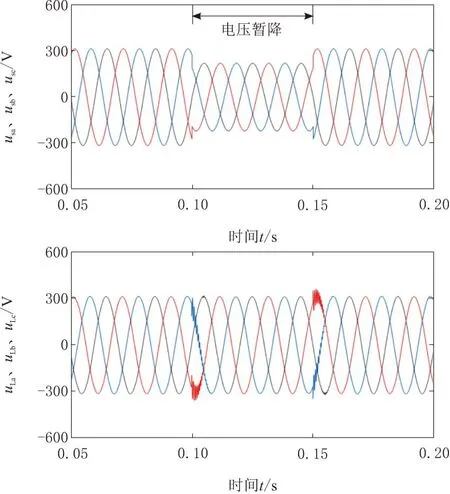
图6 电网电压暂降补偿波形

电网电压发生暂升故障时的补偿情况如图7所示,电网三相电压于0.1 s时出现暂升,幅值上升约20%,0.15 s时恢复,负载侧电压质量在补偿作用下保持正常。且在暂升与暂降故障的发生点与结束点处,补偿后的负载电压的暂态波动较小。

图7 电网电压暂升补偿波形

电网电压发生不平衡时,电压中存在负序分量,由图8可见,A相在0.1 s发生了故障,造成了三相电压不平衡现象,而负载侧电压经过UPQC补偿,保持了三相电压的幅值与对称性稳定。

图8 电网电压不平衡补偿波形

由图9可知,当负载侧负载不对称时,负载侧三相电流不平衡,三相电流中存在负序分量,根据电网侧电流波形可知,UPQC在补偿负载侧负序电流方面效果显著,保障了故障状态下负载侧电流质量。

图9 负载不平衡电流补偿波形

电网电压谐波扰动补偿如图10所示,在0.1～0.15 s间向电网电压注入幅值为电网电压10%的5次与7次谐波,在UPQC的补偿作用下,负载侧电压稳定,输出三相电压的总谐波畸变率(total harmonic distortion, THD)为2.59%,谐波得到了有效抑制。

图10 电网电压谐波补偿波形

电网电压稳定,负载变为为非线性负载时,负载侧电流如图11所示, 受谐波影响,三相电流畸变严重,而通过UPQC治理后,电网侧电流基本为正弦波形,说明基于FCS-MPC的UPQC很好地实现了对谐波的补偿效果。

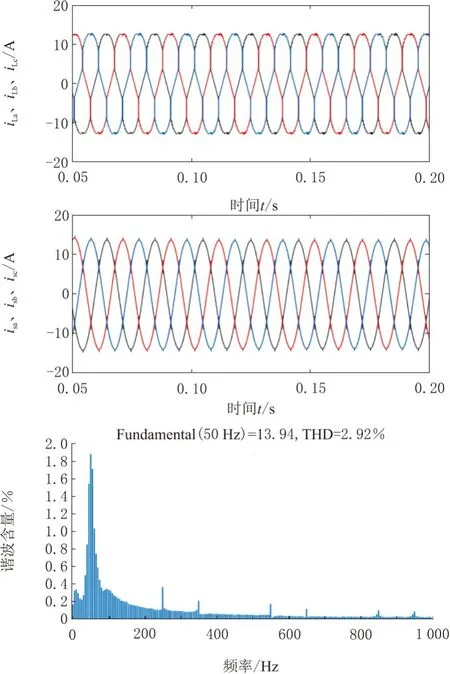
图11 负载电流谐波补偿波形

4 结束语

本文设计了一种基于FCS-MPC的TNPC结构的UPQC控制策略,并且通过仿真分析得到以下结论:

a.本文所提控制策略对补偿量检测环节进行改进,减少了滤波器和坐标变换次数;其次,本文所提控制策略建立在静止αβ坐标系上,减少了旋转坐标变换的数量,并在一定程度上降低了控制算法的复杂度。

b.通过对变流器整体数学建模,获得离散化的预测模型,通过FCS-MPC对电压电流补偿量进行直接控制,有利于提高系统的控制精度和响应速度。并在传统的MPC基础上,对分区进一步优化,减少了迭代次数,提高了控制器计算速度同时兼顾直流侧均压效果,简化了繁杂的权重因子整定工作,简化了系统结构。