信号博弈的三维重建形变识别算法

滕少华,屈政烨,霍颖翔

1(广东工业大学 计算机学院,广州 510006) 2(华南理工大学 未来技术学院,广州 510006)

0 引 言

多年来,国家对基础设施进行了大规模建设,然而旧基础设施不断老化,导致了很多安全隐患,例如桥梁变形引起的桥梁坍塌等.及时发现建筑物变形,防范潜在风险的是关系国计民生的事情,因此形变识别研究是重中之重,相关研究也成为近几年的热点,并且一部分研究在一些场景下实现了工程应用.然而,实践中复杂的条件影响了识别技术进一步推广.

传统测量中接触式测量是最主要方法,在实验室环境下可以精准地收集变形数据,但是需要人工操作,并且在复杂多变的实际场景下存在固有的局限性.例如,环境湿度和温度的变化可能导致数据产生误差,极端环境下人力无法操作,测量仪器可能失效.

为了降低环境的影响,减少人力物力,近年来,人们逐渐将目光转向通过非接触式测量的方法.其中,二维数字图像相关法[1](DIC)最早被应用,该方法通过测量选定的局部区域在形变前后的差异来实现形变识别.然而,该算法只能测量物体的面内位移与应变,容易受到背景、视角、姿态、遮挡等因素影响.三维重建技术可以解决二维数字图像只能计算面内位移的问题,得到更加精准的形变信息,是现在形变识别研究中最广泛使用的技术.其中三维激光扫描技术[2]无需接触测量目标,精度高,但是设备造价昂贵,且扫描数据需要进行复杂的处理.多视角三维重建技术通过利用多个视角的图片信息,重构物体的三维信息实现形变识别.双目视觉技术作为多视角三维重建的典型算法之一,具有非接触测量、成本低廉、几何结构简单等显著优点.

然而,双目视觉三维重建技术因为其结构特点,无法在相机位姿多变的场景下使用.双目立体视觉常规的模型在标定相机位姿后,利用位姿参数将成像平面矫正为同一平面且光轴平行的情况进行空间几何计算,得到三维信息.这就需要相机位姿保持固定,一旦相机位姿改变就需要重建标定,过程繁琐.而且在现场环境中,例如因为风力等外界因素使得相机位姿产生微小变化时,不易被发现,错误的位姿参数导致三维信息计算结果不精准,进而无法实现准确的形变识别.为解决常规双目立体视觉模型存在的局限性,运动恢复结构算法[3](SFM)使用不同角度图像序列,通过匹配相邻图像的成对特征点,求解本质矩阵得到相机位姿,实现三维重建,无需预先标定相机位姿.SFM通常利用7对匹配的特征点求解基础矩阵,特征匹配结果难免存在误匹配项,在选取误匹配项的情况下,可能会导致估计的相机位姿产生偏差,从而使得三维重建模型扭曲,最终导致结构面形变的错误识别,一些微小的结构形变无法识别.

针对上述问题,本文对双目视觉三维重建方法进行改进,提出:基于信号博弈的三维重建形变识别算法.使用博弈[4,5]方法,在已有的数据中提取知识不断迭代,使得相机位姿不断修正,并且在策略良好的情况下可以使得相机位姿不断逼近真实值,从而得到高质量的三维形变信息,进而达到准确地识别变形的目的.

算法主要包括两个方面:

1)采用信号博弈使得相机位姿参数逼近真实值,完成位姿参数估计.

2)利用最优相机位姿参数,完成三维重建并且识别形变.

基于以上条件,达到在图片拍摄时,相机相对位姿关系改变或者缺失的条件下,由不同视角的图片完成三维重建.最终对比三维信息识别出被检测物体的形变热点.

1 相关工作

视觉三维重建技术被广泛应用于物体识别[6]、距离测量[7]、变形监测[8].在形变识别方面,Tang[9]等人结合钢管混凝土柱的复杂性和凸曲特点进行了图像采集、图像预处理,生成三维点云图,利用一种改进的非线性最小二乘法对点云进行圆拟合,反求三维变形曲面得到形变,但是需要预先标定好相机,相机位姿不能随意改变,在工程现场识别效果受限.He[10]等人基于双目视觉三维重建技术提出同心圆标记方案监测边坡变形.邢[11]等人将标记物粘贴在零件表面,通过三维重建后标记物位置的改变确定零件的形变.这些研究都需要在相机固定后,标定相机位姿外参,然后获取具体物体的双目图片再计算三维信息,最终完成形变识别.然而,相机位姿一旦改变就需要重新标定外参,在极端地形环境下,例如山坡、雪地、大风或者使用无人机拍摄测量[12]等场景下,很难满足该条件.因而,近年来,一些算法通过图片估计相机位姿完成形变识别,从而避免相机位姿变化的负面影响.

为了处理复杂场景下的形变识别,SFM方法利用其对特征点估计相机位姿,还原三维信息完成形变识别,适用于极端地形条件.Xue[13]等人结合SFM与深度学习模型提出隧道形变的自动识别和准确量化方法,并运用于实际的地铁隧道中,但是深度学习模型的测试集需要人工打标签.刘[14]等人以SFM为核心得到三维信息,结合二维图像处理与深度卷积方法进行识别结构面的形变,与人工测量结果相比,裂缝宽度识别的误差在33%以内,但是同样也需人工标记变形样本.Zeng[15]等人将随机采样一致算法(RANSAC)[16]引入SFM,通过迭代求解估计相机位姿的最优参数.在增加补充点的点云数据集上,利用径向基(RBF)函数计算曲面方程修补孔洞.但是在不同场景下,该方法往往需要设置内外点阈值,不同的随机采样迭代次数和内外点阈值的设置导致不同结果,缺乏稳定性,不利于形变识别的实际应用.虽然SFM取得了一定效果,但是特征匹配中存在的误匹配项可能会导致相机位姿估计错误,识别效果不稳定.为减少错误识别,一种方法是在SFM算法的基础上增加成对特征点的个数.然而,这种做法增加了算法的运算时间,也不能从根本上解决误匹配问题.如何降低单个点在估计相机位姿时的影响,进而实现准确形变识别,是当前研究的重点.

双目视觉三维重建算法的核心是相机位姿参数估计,所以如何准确估计相机位姿,成为三维重建得到形变信息的关键.近年来博弈思想被广泛应用于机器学习以及深度学习.GAN[17]通过对抗学习的方式来训练,是博弈思想的一种经典的应用.其生成器和判别器在学习优化过程中,不断提高自身能力,最终达到一定平衡,得到最优结果.将博弈应用在估计位姿参数过程中能够提升重建的精度,并有利于完成准确的形变识别.

2 双目视觉形变识别

双目视觉形变识别主要包括:

1)预先标定双目相机的内参(焦距、畸变参数等)和外参(双目相机之间的平移旋转关系),基于此位姿关系获取两幅物体图像;

2)图像畸变矫正及双目相机位姿校正,如图1(a)所示;

图1 双目视觉相关结构Fig.1 Related structures of binocular vision

3)获取一幅图像中每个点与另一幅图像中每个点的对应关系,如图1(b)所示;

4)利用点的对应关系,通过几何关系得到三维信息;

5)前后三维信息比对识别形变,确定变形的位置.

经过上述步骤,常规算法达到识别形变的功能.实际场景中难以直接获得平移和旋转量.

3 信号博弈三维重建的形变识别

3.1 总体结构

双目视觉三维重建算法的总体思路:首先确定两次采景时,相机之间的相对位置与角度;其次利用所获得的位置角度计算三维信息;在空间坐标系对齐之后,对比三维信息进行形变计算.算法的核心是估计相机之间的位姿.

形变识别的数据共有4幅图像,物体变形前的原始状态两幅图像,以及物体变形后两幅图像.由物体变形前的两副图像,可得到一组三维信息;同样,由物体变形后的两副图像,也可得到一组三维信息.注意图像应该在不同的视角与机位下拍摄,图像需要互有重叠.由物体变形前后对应的两组三维信息得到形变区域.

具体的步骤为:1)首先对图像进行畸变矫正;2)然后进行特征点识别,并对四幅图像两两进行特征点匹配;3)对6组匹配结果进行约束,进而获得4幅图像中共有的同名点(各图像中的点对应物体上的同一个点);4)利用变形前图像的同名点求解拍摄时相机位姿参数,完成三维信息重建;5)同理得到变形后物体的三维信息,对比前后两个时期的三维信息,即可得到形变信息.如图2所示.

3.2 相机位姿估计

相机位姿参数估计是三维信息计算的关键,也关系着形变识别的效果.为了方便后续描述,对相机位姿参数进行说明.

其中q∈3×1代表β坐标系相对α坐标系的平移量,R∈3×3则为相对的旋转量.图像在经过SFIT特征匹配后存在多组同名点,例如a1=[x1,y1]T,a2=[x2,y2]T,其对应真实的点a′∈3×1.以α坐标系为三维世界坐标系,a1和a2对应的坐标表示为a′∈3×1和a″∈3×1.只有ρ确定了,a′和a″的三维坐标才能确定,才能进一步利用空间几何得到a,所以估计相机位姿是算法的关键.

位姿参数估计过程中结合信号博弈来得到最优参数.信号博弈中包含两个角色,信号发送者(参数评判器)与信号接收者(参数生成器).评判器向生成器发出参数的评分信号,生成器收到信号后,根据信号选择行动.最终的收益由双方共同决定.

通过生成器和评判器之间的博弈达到均衡状态,此时评判器认为真实数据和生成数据几乎是相同的,如此便得到了位姿参数的最优解.与RANSAC算法类似,都属于随机性方法.RANSAC通过随机选择部分同名点作为内点计算位姿参数,每次运行可能取得不一样的结果.本文方法则是直接随机生成位姿参数,得到模型,然后在所有预筛选过的同名点上进行评估,根据评估信号获取数据中潜藏的位姿信息,具有一定的选择倾向性,使得后续的随机生成参数,每次迭代后准确度稳定上升.

3.3 高斯分布法生成相机位姿参数

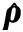
算法1.高斯分布相机位姿参数生成算法

输入：特征匹配后的同名点.

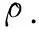
a)设定期望值为θ,各维度间独立且方差微小的概率密度分布P.

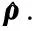
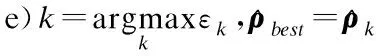
g)转到步骤b).

其中,带权重系数协方差矩阵的计算方式为:

Cij=Cov(Xi,Xj,ε)=E(XiXj,ε)-E(Xi,ε)E(Xj,ε)

(1)

其中,带权重的期望计算方式为:

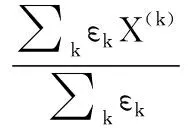
(2)

则带权重系数ε的高斯分布概率密度函数为:

(3)

3.4 空间几何法计算三维信息

图3 三维信息计算Fig.3 3D information calculation

(4)

其中:

a′=[x1,y1,1]T

(5)

a″=q+R[x2,y2,1]T

(6)

η=N(a′×(a″-q))·(a′-a″)

(7)

N(a′)将向量a′进行单位化.由下式解出未知数m1.

(8)

3.5 位姿参数评估

(9)

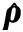
4 三维坐标对齐及形变位置计算

将上述方法分别用在变形前后的图像数据上,得到物体变形前和变形后两组三维信息.aa∈3×m为变形前的三维信息,ar∈3×m则对应变形后的三维信息.为了进行对比,需要进行坐标系转换,最终进行比较得到形变.

由于变形后部分点产生了位移,直接用两组点计算转换关系可能会导致变形部分的点扭曲,降低形变识别的精度.S预先对两组点进行筛选,减少这种影响,然后通过E∈3×m对ar进行平移,通过T∈3×3对ar进行旋转,最终将坐标系γ中的点转换至坐标系α中完成对比.S=diag(λ1,λ2,…,λm)为筛选两组点的选择矩阵,λ取值为0或1,ξ为大于0小于1的常数.

为了求解最优转换关系T和E,同时提高求解过程的稳定性可以同样用上述估计位姿参数的方法.首先找到3个较为分散的点aαi,aαj,aαk,(i≠j≠k),且构成面积最大.利用这3个点以及其对应的3个点aγi,aγj,aγk,得到初始值T0和E0以加快求解速度.利用生成方法产生与T0和E0不同但相接近的转换关系.计算转换关系的评分d,基于d进行优化得到较为准确的转换关系,并筛选一部分点.对上述过程进行迭代,最终得到一个最优的转换关系,使得对准更加准确.

先求两组点aαi,aαj,aαk和aγi,aγj,aγk的初始偏移量E0和初始旋转量T0.

(10)

T0=[aαi,aαj,aαk][(aγi+E0,aγj+E0,aγk+E0]-1

(11)

然后基于初始值得到高斯分布概率密度函数P,同时有评判标准d,因为同名点经过预筛,误匹配较少,所以在充分学习后,可以得到最优的坐标系转换矩阵,最终进行准确的形变识别.

E=E0+Δe

(12)

T=T0+Δt

(13)

(14)

s.t.tr(S)=|ξm|d=T(aγ+E)-aα

(15)

对准坐标系后,d中对应了每个点产生的位移,也对应了变形的大小,最终用热点图展示出对应的变形位置以及大小.

5 实验结果分析

最后用两组数据验证算法的可行性,第1组用手机拍摄的真实图片进行验证,第2组利用三维建模得到的图片进行形变识别的验证.

5.1 实验1

实验1.数据为手机拍摄不同角度的4张图片,如图4(a)、(b)、(d)、(e)所示,获取图片时保证图片中物体有重叠的部分.不同于常规双目立体视觉需要相机位置和角度固定,然后进行外参标定后获取图片,本文的方法无需预先标定外参,图片拍摄的角度也相对自由,更便于实际环境下应用.

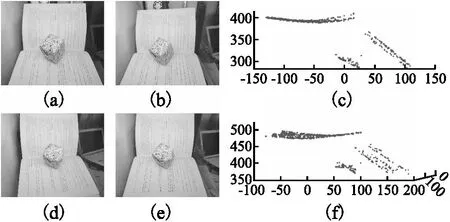
图4 实际物体变形前后的图像及重建效果.(a)、(b)物体变形前的图像(c)变形前的三维点云(d)、(e)物体变形后的图像(f)变形后的三维点云Fig.4 Image before and after deformation of the actual object and reconstruction results.(a)、(b)Image before deformation of the object(c)3D point cloud before deformation(d)、(e)Image after deformation of the object(f)3D point cloud after deformation

如图 4(c)、图4(f)所示,重建点云图中点分布规律轮廓清晰和真实物体非常接近,且噪声点较少,变形前后的点云几乎仅在变形处存在不同.

通过前后三维信息的对比得到物体变形的热点区域,但是没有标准的环境难以量化位姿参数,无法计算参数的准确性.因此实验2使用3DsMAX构建数据进行实验.

5.2 实验2

5.2.1 三维重建效果验证

实验2.对柱子的三维模型进行三维重建及形变识别.首先用未变形的两幅图像来验证三维重建的效果.未变形时所对应的两幅图像如图5(a)、图5(d)所示.

图5 三维模型的图像及重建效果.(a)、(d)不同视角的图像(b)、(e)SFM重建效果(c)、(f)本文的重建效果Fig.5 Images of 3D models and reconstruction results.(a)、(d)images from different perspectives(b)、(e)reconstruction results of SFM(c)、(f)reconstruction results of this paper

使用SFM和本文的算法分别进行三维信息计算,对比各自三维重建的效果.使用SFM对三维模型进行重建得到的点云图,如图5(b)、图5(e)所示,图5(b)为俯视角的点云图,图5(e)为正面视角的点云图.可以观测到点云形状产生倾斜扭曲,圆柱曲面变平缓,与三维模型有较大的差别.因此倘若利用直接用SFM计算变形前后的三维模型的点云,进而对比获得形变会有较大误差.

利用本文算法对三维模型进行重建同样得到点云图,如图5(c)、图5(f)所示,和SFM结果相比,点云轮廓清晰,与三维模型更接近.

5.2.2 相机位姿参数验证

在3DMAX中可以准确获得相机拍摄位置,从而得到两个相机之间的真实的位姿关系,与本文算法计算的结果进行比较,最终得到位姿参数的准确性.

相机的相对位置关系为q,为了使表示更为直观,旋转关系R被分解为相机朝向v和水平旋转k.两个相机之间的真实的位姿关系q,v,k的对比结果见表1、表2以及表3.同时将本文和SFM方法计算得到q,v,k对应结果的误差对比,见表4.

表1 q的人工评估得分对比Table 1 Comparison of human evaluation scores for q

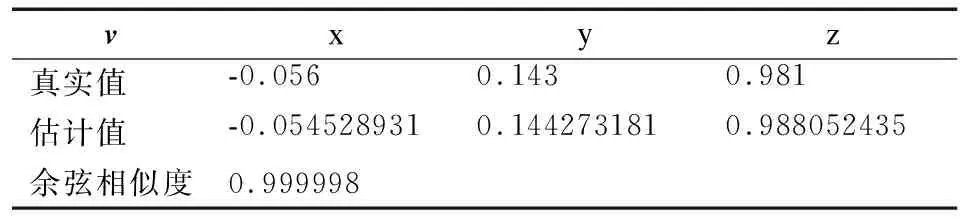
表2 v的人工评估得分对比Table 2 Comparison of human evaluation scores for v

表3 k的人工评估得分对比Table 3 Comparison of human evaluation scores for k

表4 两个方法在三维模型数据上的效果对比Table 4 Comparison of the effects of the two methods on 3D model data

q与实际方向偏移了2.85度,相机朝向v方向和实际方向偏移了0.114度,水平方向与实际偏移了0.114度,计算得到参数误差较小.

5.2.3 三维柱体模型形变识别

准确的相机位姿能够得到高精度的三维信息,进而精确地完成形变识别.为了进一步得到算法识别变形的范围,实验验证.用3DMAX构建了直径为19.2的柱子,产生不同大小的形变.当变形至直径为19.8时,算法尚能较清晰识别出形变区域,进一步构造更小的形变后难以得到形变区域.最终得到算法可识别相对柱体直径而言产生3%及以上的形变.

形变后柱体模型得到点云图以及形变识别效果如图6所示.原图人眼无法识别出是否产生了形变,但是在算法得到的三维点云中可以观测到柱子侧面凸起,且热点图清晰展示了变形的位置.

图6 三维模型变形后的数据Fig.6 Data after deformation of 3D model

5.3 实验结果分析

实验1利用手机拍摄的图片,进行三维重建,过程中无需预先标定相机外参,然后保持位姿不变获取图片,体现了该方法的方便快捷.得到三维信息后识别到物体形变的热点,表明其识别形变的有效性,也侧面验证了三维信息的准确性.实验二利用3DMAX构建物体,和SFM相比本文算法得到的三维点云更加准确,同时得到的位姿参数也更加准确.

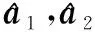
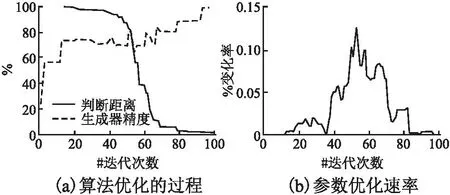
图7 模型优化参数的结果Fig.7 Result of optimizing the parameters of the model

总体而言,实验验证了博弈思想使用在估计参数时的作用,在通过评判器和生成器合作迭代协调后,参数得到显著优化,同时准确度逐步提升,较为稳定.同时基于参数结果,得到三维信息后,对比后利用热点图可以准确展示物体形变的位置和大小.

6 结束语

本文采用信号博弈的方法估计相机位姿参数,提高三维重建精度,完成形变识别.无需预先标定双目相机之间的位姿关系,拓展了适用的场景,有利于更复杂实际场景下的运用.而且过程中,有着更少的人工参与,具有更高的自动化程度.同时算法采用信号博弈的方法估计相机位姿,得到的参数更加准确,重建精度更高,更有利于计算形变.通过两组实验进行验证,第1组通过手机随意拍摄的图片进行实验,直接识别了物体的形变,设备简单且无需预先标定双目相机位姿.第2组对三维模型进行了形变识别检测,实验验证了算法的有效性.但两个实验都是模拟生活场景,后续有待在真实的相关场景下进行验证.