改进Q-Learning的路径规划算法研究

宋丽君,周紫瑜,李云龙,侯佳杰,何 星

(西安建筑科技大学 信息与控制工程学院,西安 710055)

0 引 言

最优路径规划及路径规划过程中的有效避障是目前移动机器人多个领域都需要解决的关键问题[1],当前针对此问题提出的方法主要包括:人工势场法、遗传算法[2]、神经网络法[3]、强化学习法[4]及A*算法[5]等等.在静态环境下的路径规划相对容易完成,但在存在随机障碍物且环境时刻变化的动态环境中,则无法采用静态环境下的路径规划方法完成指定任务[6].本文主要针对复杂随机障碍物的环境下进行动作选择策略规划以及环境中存在动态障碍物的突发情况的路径规划进行研究.

Q-Learning算法是由Watikins提出的,该算法可用于解决移动机器人的路径规划问题[7],目前机器人在人类不可到达或危险未知的环境下完成任务较多采用Q-Learning算法.文献[8]等将神经网络与Q-Learning算法相结合,不但可以用来解决不同环境下的路径规划问题,还能够提升算法的收敛性能,但是未能解决动态地图下的路径规划.张福海等通过对障碍物信息离散化、奖励函数连续化等方式提升了强化学习算法在路径规划上的训练效率[9].文献[10]将策略结合作为创新点,作者提出将贪婪策略和玻尔兹曼概率选择策略进行整合,通过改变选择策略达到避免陷入局部最优的效果.文献[11]对加快算法收敛速度进行研究,作者以函数逼近的方法降低Q函数的维数,达到提升收敛速度的目的,但该方法会增加探索重复率.通过上述前人研究可以发现,虽然国内外的学者们对Q-Learning算法在解决路径规划问题上已有一定研究,但研究热点依然聚焦于解决局部最优和提升收敛速度[12].王鼎新针对AGV静态环境路径规划提出了一种基于人工神经网络的Q-Learning算法[13].彭玲玲等提出栅格法建立地图环境,通过改进Q-Learning算法使机器人在静态且存在复杂障碍物的环境里能够更快抵达终点,但该算法只针对静态避障,无法应用于存在动态障碍物的环境中[14].因此可以看出以上学者研究方向均未同时涉及动态环境下路径规划及轨迹平滑处理,因此在改进探索策略提高算法效率的基础上,对动态环境的路径规划研究及轨迹平滑处理为本文研究的核心内容.

针对以上问题,本文提出了一种改进Q-Learning算法,对Q-Learning算法的选择策略探索因子及深度学习因子进行改进,融合全局启发式搜索遗传(GA)算法防止并其陷入局部最优,同时按阶段进行探索将Q-Learning算法应用在动态连续环境中并提高了算法收敛速度,最后采用贝塞尔曲线对局部拐点路径进行平滑处理加强了算法的工程应用价值;最后搭建仿真实验平台及实物实验平台对算法效率及可行性进行验证.

1 理论基础

1.1 强化学习算法

强化学习(reinforce-learning,RL)是一个从环境状态到动作映射的学习[15],该算法的学习不依赖监督信号而是依赖个体在环境中的得到的反馈回报信号,个体的状态即下一步行动根据得到的反馈汇报信号更正,以此实现奖励的最大化从而使得强化学习具有较强的自主学习能力.

1.2 传统Q-Learning算法原理

Q-Learning算法归属于强化学习,该算法主要包含:机器人、状态、动作、环境、回报和惩罚[16].Q-Learning算法中的Q表是机器人自主学习得到的反馈结果,即机器人与环境交互感知后的结果,因此在Q-Learning算法中更新Q表就是机器人与环境的交互过程.

机器人在当前状态s(t),选择动作a,通过环境的作用,形成新的状态s(t+1),并产生回报或惩罚r(t+1),通过公式(1)更新Q表后,若Q(s,a)值变小,则表明机器人处于当前位置时选择该动作不是最优的,当下次机器人再次处于该位置或状态时,机器人能够避免再次选择该动作.重复步骤,机器人与环境之间不停地交互,就会获得到大量的数据,直至Q表收敛.Q-Learning算法使用得到的数据去修正自己的动作策略,然后继续同环境进行交互,进而获得新的数据并且使用该数据再次改良它的策略,在多次迭代后,最终会获得最优动作.算法价值函数的更新公式为:

Q(si,At)←Q(si,At)+

α[Rt+1+γmaxαQ(si+1,a)-Q(si,At)]

(1)

公式(1)中Rt+1为移动机器人t+1步的奖励,a为状态si+1能执行的动作,状态si,si+1∈S,S为状态空间;动作a∈A,A为动作空间;a为学习效率,学习效率越高,Q值收敛越快,也更容易振荡;maxαQ(si+1,a)表示选取能够使Q(si+1,a)取值最大的动作;γ为衰减因子,表示奖励对选择动作的影响程度大小,Q-Learning算法的依赖收敛关系为前后依赖.

2 改进Q-Learning路径规划算法

2.1 Q表初始化

初始化Q值是指在Q-learning的初始学习阶段引入对环境的先验知识,将任意位置下的栅格到目标点栅格的欧式距离定位D(xi,xg),到起始点栅格的欧式距离定位D(xi,xx),取:

D(xi)=(1-η)·D(xi,xg)+η·D(xi,xx)

(2)

使用D(xi)的线性归一化数值来初始化各个状态的Q值(η∈(0,0.2),η为权重系数),以此来避免盲目探索,使得算法在前期就有目的地选择下一个路径点,大幅提高算法的收敛速度,同时将动作空间离散为A∈{0°,90°,180°,360°},以提高训练速度加快收敛,在栅格环境内对应动作状态向右、向上、向左,向下.

2.2 动作选择策略

在Q-Learning算法中,惯用的搜索决策主要归类为直接搜索和间接搜索,直接搜索即为有先验知识的前提下探索,若将状态划分为已知和未知两种,在已知状态下根据现有的经验知识进行的位置情况下的探索即为间接探索.文献[17]采用经验指导决策的方法进行探索,对当前实验对象的奖励机制做分析,若获得奖励则利用采用当前经验,若受到惩罚则选择探索.间接搜索是当前Q-Learning算法最为常用的探索方法.

本文针对算法搜索时间与学习速度的问题做了平衡改进,选用ε-greedy贪婪法,利用概率的突变性优化探索和利用的选择,即实验对象以ε概率进行探索,以1-ε的概率选择放弃探索,并执行最高奖赏的动作.该方法在平衡探索和利用的问题上,引入了探索因子ε,因此改进后的搜索策略即可充分利用先验知识,也可在缺失先验知识的情况下选择探索.公式如下:

(3)

从公式(3)中可知,选取使得动作值函数为最大值的动作的概率为1-ε+ε/|A(s)|,选择其他的动作的概率ε/|A(s)|,ε∈[0,1].由于该探索效率会随着算法运行强度增加而降低,结合本文的研究分析设计一种基于ε-greedy贪婪法的新型策略,根据阶段探索步长的栅格有效状态对搜索概率进行适当增减,以保证最大效率,当前环境反馈的回报值较大时为避免陷入局部最优保持探索效率,当前有效状态即回报值减小时算法处于局部范围的寻优因此可提高探索效率,在探索步长的阶段寻优基础上增加依据环境回报状态实时调整的探索因子,公式如下:

(4)

式中ε是探索概率;λ是衰减系数设置为10确保探索效率与环境回报状态呈负相关;Δx是阶段补偿探索的有效回报状态;N是步长总数量.

2.3 基于GA算法的Q-Learning算法

本文针对Q-Learning算法易陷入局部最优的缺点,在Q-Learning算法的步骤中融合GA算法,遗传(GA)算法最初是由John Holland在1960年开发的,又叫进化算法是一种启发式搜索方法[18].该算法的主要特点是群体搜索以及个体信息交换.遗传算子新个体的产生源于对被选中的个体进行的交叉、变异操作,提高逐代进行选择、交叉、变异来模拟自然进化过程,在本文研究的问题中最优路径即为最终得到的最优个体.使用模拟二进制交叉,使其搜索范围比传统的交叉更大,以此避免Q-Learning算法陷入局部最优解,从而使移动机器人在陷入局部极优区域时逃脱,并继续向目标点移动.同时本文针对传统Q-Learning算法应用于实际场景中的缺陷做出改进,使其适用于动态障碍物环境中,同时提高效率,实现高效率的实时避障.

根据马尔可夫决策首先给定一个状态集S,一个行为集A.s∈S,a∈A.Q(s,a)表示的是s状态下选择行为a的分数,Q用表格表示.有了Q值之后,即可知道当在状态s时候的行为选择,进而选择最大Q值的a动作.

给定3个状态s1,s2,s3,s4,假设它们每个只有一个动作分别是a1,a2,a3;s4没有动作.在s1状态下进行a1动作(s1,a1)的奖励为r1,执行a1进入到s2,(s2,a2)的奖励为r2,执行a2进入到s3,(s3,a3)的奖励为r3,执行a3进入到s4无奖励.

设γ表示衰减因子,0到1之间,根据上面的状态动作过程,得到:

Q(s1,a1)=r1+γ·r2+γ2·r3

(5)

式中γ表示现在s1状态选择a1动作跟未来的奖励关系大小的程度.γ为0时,说明现在的选择不会影响未来.由此可以得出:

Q(s2,a2)=r2+γ·r3Q(s3,a3)=r3

(6)

由此可得出规律:

(7)

归纳得到公式:

Q(si,ai)=ri+γ·Q(si+1,ai+1)

(8)

由此可知Q函数表格应符合上述公式,若:

ri+γ·Q(si+1,ai+1)-Q(si,ai)>0

(9)

说明Q小了,加一个正数t,即:

Q(si,ai)=Q(si,ai)+t

(10)

Q(si,ai)=Q(si,ai)+

a(ri+γ·Q(si+1,ai+1)-Q(si,ai))

(11)

实际应用中s会有多个动作选项,需要拿出状态最大行动的Q值,即:

Q(si,ai)=Q(si,ai)+

a(ri+γmaxQ(si+1,A)-Q(si,ai))

(12)

为避免陷入局部最优,引入GA算法,选择、交叉、变异操作:

选择操作:

选择操作使用锦标赛算法,具体步骤如下:

1)确定每次选择的个体数量,即从Q-Learning每次的多个动作选项si中随机选择n条规则.

2)随机在种群中选择一定数量的个体构成小组,筛选出适应度值最好的个体进入子代种群.

3)重复步骤2,直到子代种群目标规模,以此生成新个体,设置子代种群的大小为规则种群的1/2,即代沟为0.5.

选择开始时,个体生存的概率会比较大,为了保持整个群体的多样性,一些结果不太优秀的个体也会被选择留下来[19].随着进化代数的进行,搜索范围越来越小,选择的标准也会越来越严格,使用选择方式的选择概率为:

(13)

式中:f(aj)是个体aj的适应值,p(aj)是个体aj被选择的概率.

交叉操作:使用模拟二进制交叉,配对组合随机选择,每一对都需要进行单点交叉,交叉概率设置为0.9,伴随有2个子规则产生.

变异操作:子规则根据变异概率0.03进行变异.当一个条件位被选择进行突变,则以均等概率将该位变为0或1.具体计算方法为:

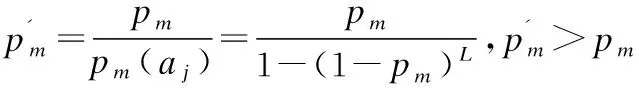
(14)

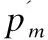
在此基础上设置移动机器人同时按阶段探索最优迭代步长次数,首先根据先验的环境信息对从起始点至终止点的最大步长进行估计,并将环境下的最大步长设为2x,将其均等分为N个阶段,每阶段探索步长为2x/N.从第一个阶段开始对环境分阶段进行m次探索,并在更新Q表中寻出该阶段的最优动作选择,以此为基础依次对其他阶段的动作进行最优选择,最终结果即为此阶段的最优路径,以此为基础进行环境探索以此规划实时的避障路径,由于传统Q-Learning算法搜索范围有限仅探索下一步动作,因而根据当前环境信息结合融入的GA算法,移动机器人可进行深度探索,同时获取路径上的动态障碍物位置信息,以此规划全局及局部路径避免陷入局部最优.

本文在传统Q-Learning算法值函数的更新函数中加入深度学习因子ω∈(0.5,1),用于确保Q值收敛,并对移动机器人探索过程的第一、二步获得的回报进行权衡,其中ω参数设置的主要目的为保证第一步的回报权重大于第二步.改进后的值函数更新规则为:

Q(si,ai)=Q(si,ai)+

(15)

式中:Q(si+2,a)为后两步动作状态Q值,改进后的算法能够促使移动机器人更早的确定目标点同时判断路径过程中的障碍物,尽早的更新函数Q值.

2.4 路径平滑处理

目前在大多数研究中使用的路径平滑处理主要分为全局和局部优化,全局优化是一种综合性的优化处理,当移动机器人处于复杂多随机障碍物的环境中,全局路径的平滑处理可能会导致处理后路径与障碍物产生交叉,失去原规划路径的可行性.

因此在确保路径规划可行性的前提下,以此为研究基础结合本文环境背景,采用局部路径优化,使局部即拐点处的路径具有共同的切向速度和曲率实现平滑过渡.贝塞尔曲线的控制能力和线段平滑处理能力在同级别几何曲线中稳定较高且相对可靠,基于此本文基于贝塞尔曲线进行局部轨迹优化.

贝塞尔曲线是一种运动轨迹曲线,由n个点在n条线段上匀速运动,生成的轨迹曲线空间,n次贝塞尔曲线上的某点的差值的表示公式为:

(16)

式中t为隐形表达的独立变量,bi为贝塞尔曲线第个i控制点,Bi,n(t)为n次Bernstein基函数,其表达式为:

(17)

路径规划中常用到的处理平滑路径的曲线为三次贝塞尔曲线,但是三次贝塞尔曲线不能加入曲率约束,因此本文使用四次贝塞尔曲线以同时满足运动学约束、初始状态约束、目标状态约束以及曲率连续约束,其参数化表达式如下:

(18)

p(δ)=p0(1-δ)4+4p1(1-δ)3δ+6p2(1-δ)2δ2+

4p3(1-δ)δ3+p4δ4

(19)

公式(19)中,p0、p1、p2、p3、p4表示3个连续的初始控制点.以图1的局部路径为例,分别在连续多拐点场景图1(a)及大角度拐点场景图1(b),采用四阶贝塞尔对拐点路径进行平滑处理,结果如图1所示,提高了路径平滑度,避免了在实际工程项目中移动机器人不必要的损耗,提高了运动的连续性和工作效率.

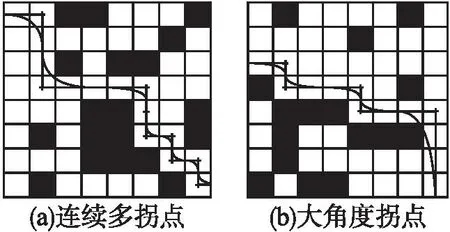
图1 轨迹平滑处理Fig.1 Smooth processing graph of track

3 实验与分析

3.1 静态障碍物环境下的仿真实验

为了验证本文算法的有效性和可行性,本节选取20×20特殊地形的栅格地图模型和障碍物占比分别为20%、30%和40%的30×30栅格地图模型作为实验环境,如图2所示,图中圆圈表示起始位置,五角星表示目标位置,黑色方块部分作为环境中障碍物的模拟障碍,即移动机器人需要识别避障、局部路径规划的部分.

图2 随机障碍物环境下的对比试验Fig.2 Comparative test under random obstacle environment

实验首先在固定障碍物地图的场景中分别对传统Q-Learning算法和本文改进的Q-Learning算法进行实验.对其寻找到最优路径的迭代次数及所需时间进行横向对比进一步验证算法可行性.

3.1.1 特殊障碍物环境下的仿真实验

在特殊障碍物实验中选用如图3所示的20×20障碍物占比28%的特殊环境地形,该地形相较于随机障碍物,障碍物具有体积大,且部分呈现凹形的特点,因此处理该类特殊障碍物环境下的地图会给算法增加额外的负担.

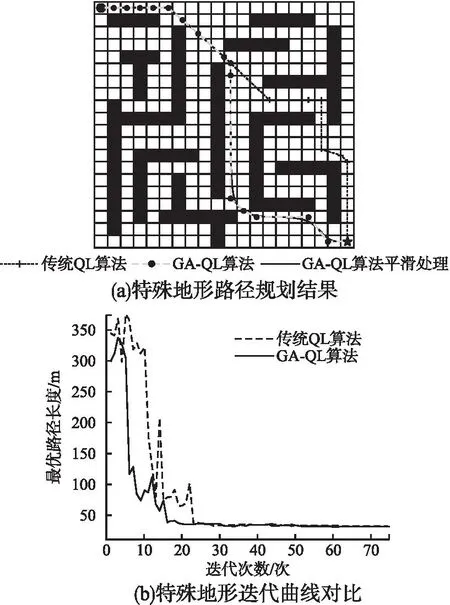
图3 特殊障碍物环境下的仿真实验Fig.3 Simulation experiment under special obstacle environment

3.1.2 随机障碍物环境下的仿真

在随机障碍物实验中,分别选用障碍物占比依次增加百分之十的30×30栅格地图模型作为实验环境,对不同复杂程度的地图环境进行实验验证.

3.1.3 静态障碍物环境下的仿真实验结论

图2所示的复杂障碍物环境下GA-QL算法相较于QL算法路径长度优化了4.73%,速率提升了47.57%,由于复杂路径下U型障碍物及障碍物体积较大,所以GA-QL算法拐点数改进并不明显,但平滑处理后路径相较于QL算法有较大的提升,且局部路径平滑处理不会对先前路径造成影响,避免了与障碍物交叉导致规划路径失败的事件发生,更适用于此类复杂障碍物地图模型;由图4的仿真结果可以看出,随着障碍物占比的增加,GA-QL算法显示出了更优秀的路径长度选择并提高了算法效率,在3种环境下路径分别优化了9.56%、15.69%和18.8%,在寻优时间上分别优化了69.38%、65.19%和67.68%,且相较于传统QL算法,本文提出的GA-QL算法所需迭代次数也大幅度减少,由表1实验数据可以看到,无论在复杂障碍物环境还是随机障碍物高占比的环境地形,GA-QL均能快速逼近最优解,减少迭代次数,提高算法效率,找出更优的全局路径,平滑后的路径能够让算法同时满足移动机器人的动力学约束,更适用于工程应用中.

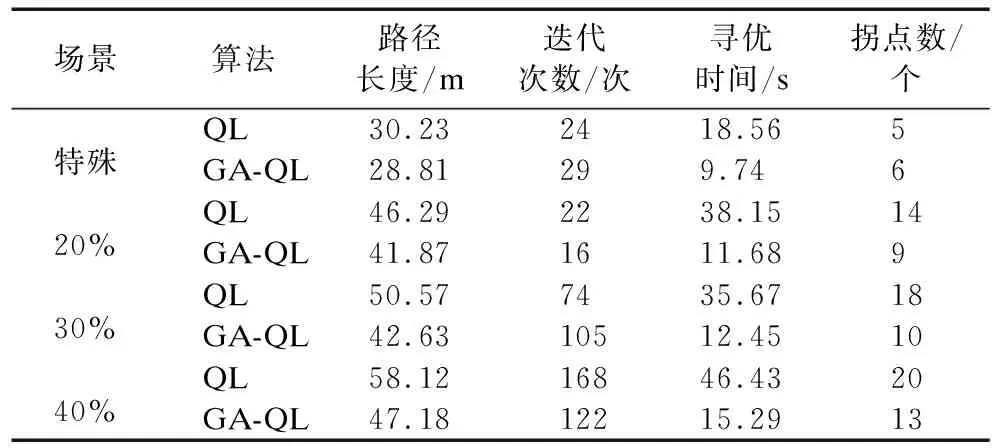
表1 仿真结果Table 1 Simulation results

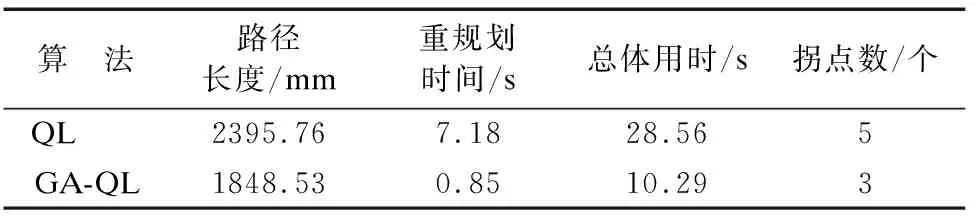
表2 实验结果Table 2 Experimental result

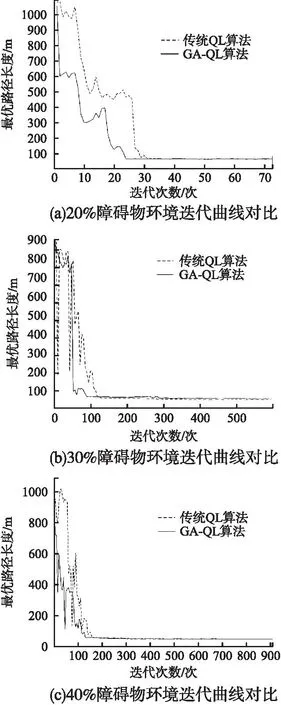
图4 随机障碍物环境下的迭代曲线对比Fig.4 Comparison of iterative curves in random obstacle environment

3.2 随机动态障碍物环境下的仿真实验

采用算法在地图上生成随机动态障碍物,如图5所示在动态障碍物实验中环境随机变化,除主要固定障碍物外,存在一定区域有随机障碍物出现或移动的地图环境,动态避障实验条件:设定环境信息n=20,最大步长2n=40,阶段数量N=4,探索次数m=5(第1步为初始状态下的全局探索设为Step 0),衰减因子g=0.2,学习效率a=0.6,深度学习因子w=0.8.

图5 动态环境分段路径图Fig.5 Dynamic environment segmentation path map

图5仿真实验结果显示,在引入随机障碍物后移动机器人能够及时反映进行避障,图5中Step 1～Step 4为分阶段动态避障实验结果,各阶段均能规划出局部最优路径,在Step3陷入盲区死角时也能探索当前地图及时采取后退动作,创新规划局部路径.图6为最终的全局路径规划图,其中路线与黑色障碍物重叠部分表示前后环境地图发生改变,先前路径经过的位置还未出现动态障碍物,由此可以看出改进后的GA-QL算法在动态环境下可实现全局及局部最优路线规划.

图6 动态环境路径规划结果Fig.6 Dynamic environment path planning results

3.3 机器人路径规划实验验证

3.3.1 实验场景搭建

动态环境场景仿真实验采用随机障碍物栅格地图,除去常规场景下的固定障碍物后外加随机出现或移动的动态障碍物,移动机器人需学会避开对方,重新规划局部最优路线,以此为背景使用轻舟机器人作为实验机器人,将其应用于实际场景中,在考虑移动机器人可移动范围后,加入随机动态障碍物,静态障碍物环境布置如图7所示,其中SP和EP分别为起始点和终止点设置,环境中4个立方体是静态障碍物,5个长方体是模拟墙壁,移动机器人需要进行全局路径规划以规划出一条可行路径,同时在机器人移动过程中加入动态障碍物对其路线进行干扰.

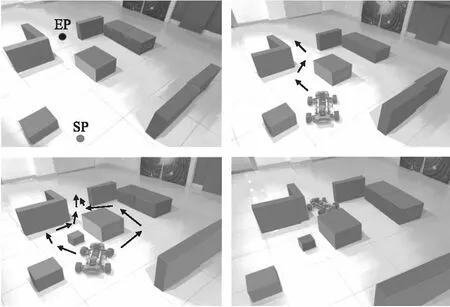
图7 移动机器人路径规划结果Fig.7 Mobile robot path planning results

3.3.2 机器人路径规划实验

实验采用505mm×350mm×165mm大小的移动机器人,参考所使用机器人体积大小,实验场地每一个正方形地砖划分为一个栅格,每个栅格边长为500mm,以此计算移动机器人在改进的Q-Learning算法路径规划下移动的步长,在该实物实验中存在车辆转弯半径等因素,在实际应用中传统Q-Learning算法存在效率低、易陷入局部最优、无法躲避动态障碍物,且拐点较多移动机器人启停频繁影响效率的问题,而本文改进的Q-Learning算法具有更优的性能表现,如图7所示实验可以看出在原路径上出现随机障碍物时,实验机器人可以及时反映避障并结合目标点规划出局部最优路径,且对于拐点处理更为平滑,减少了机器损耗,实验规划路径总长度为1848.53mm,相较于传统算法的路径缩短了22.84%,检测到动态障碍物到规划出新的局部路径用时0.85s,相较于传统算法提高了88.16%,总体用时10.29s,相较于传统算法提高了63.97%,融合后的平滑路径减少了移动机器人行驶过程中的启停,使路径完成度更高,能够更好的完成实际场景下的路径规划.

4 结 论

本文针对Q-Learning算法在路径规划中出现的收敛速度满,学习效率低,动态地图路径规划效果不好,不平滑问题,提出一种改进的Q-Learning算法的路径规划,使用距离定位坐标、更新了选择策略,加入深度学习因子并融合遗传算法,最后在保证路径安全可行性的前提下在局部路径采用贝塞尔曲线对拐角进行过渡,增强了算法的可实用性.最后通过多类型障碍物场景地图的仿真实验及实物实验得出了如下结论:

1)改进的Q-Learning算法在复杂障碍物地图和障碍物高占比地图下的路径规划路径长度及算法效率均较传统算法更具有优势.且随着环境难度的增加,本文所提算法在收敛速度、算法效率及路径长度上的优化效果都更为显著.

2)改进的Q-Learning算法由于添加了阶段性节点搜索,能够适用于动态障碍物环境中,且阶段节点选择与环境地图大小呈正相关,即避免了运行资源的浪费,又能够及时躲避动态障碍物,探索局部最优路径.

3)改进的Q-Learning算法中引入了贝塞尔曲线对局部路径拐点进行平滑处理,在实物实验中结果显示该处理减少了移动机器人实际场景下路径规划过程中的启停行为,减少了不必要的损耗,增强了算法的可实用价值.因此改进后的算法对环境有更强的适应能力,能够更准确,更快速地进行路径规划.