基于改进四参数法的法兰螺栓连接预紧力优化

张阳，赵晶

（沈阳工业大学 机械工程学院，沈阳 110870）

0 引言

由于螺栓预紧弹性的相互作用，会导致已预紧螺栓的预紧力会发生改变，这大大降低了法兰螺栓连接的可靠性和使用性能。因此，针对由螺栓弹性相互作用的研究已成为螺栓法兰连接高性能装配的热点。

Van Campen等[1]于1969年提出了弹性相互作用系数法，Bibel等[2-3]扩展了该方法。Zhu等[4]使用有限元和实验方法研究了弹性相互作用的影响。基于弹性相互作用系数法，确定螺栓的初始预紧力，最终得到均匀的目标预紧力。马跃等[5]的研究表明多轮次预紧能够有效降低残余预紧力的分散程度，并将该方法应用到某型盘式发动机螺栓组预紧，得到了令人满意的结果。Nassar等[6]建立了有限元模型，研究了预紧顺序、垫片加载和卸载历史及预紧力水平对弹性相互作用的影响，通过实验验证了有限元方法的有效性；使用逆序列法确定螺栓的初始预紧力，最终得到满意的结果。Coria等[7-8]基于弹性相互作用系数法开发了四参数法，在保证结果准确性的条件下大大缩减了使用成本；同时，验证了四参数法在多轮次预紧时的有效性。

以往的文献中对无垫片法兰螺栓连接的弹性相互作用的研究还较少，但对很多工业设备来说，采用的往往是无垫片法兰螺栓连接，尤其是透平压缩机分体式机壳这种多螺栓密排连接的压力容器[9]，其均匀的预紧力是保证密封性能的前提。因此，应用有限元分析方法，分析研究无垫片法兰螺栓预紧力分布情况，根据现有方法中四参数法使用成本低的特点，采用该方法解决预紧力分布不均问题，探讨其适用性，最后将四参数法予以改进，进一步提升其结果准确性，为解决透平压缩机分体式机壳螺栓预紧力分布不均问题提供参考。

1 四参数法

1.1 原理简介

该方法是基于弹性相互作用系数法改造而来，目的是通过一轮或两轮预紧，使全部螺栓获得均匀的目标载荷。建立螺栓初始载荷和最终载荷的矩阵方程：

式中：Sf为全部螺栓预紧后的螺栓最终载荷矩阵；Si为螺栓的初始载荷矩阵。矩阵Sf和Si中的元素一一对应，即矩阵Si的元素Sik是螺栓k的初始载荷，Sf的元素Sfk是螺栓k的最终载荷。

那么在计算出矩阵A后，应用螺栓最终荷载Sf以反求螺栓的初始载荷Si，使用下式计算：

1.2 矩阵A参数计算方法

表1给出了四参数法矩阵A中参数的计算方法，该方法仅考虑螺栓两侧与其相近的4个螺栓的影响，无需模拟螺栓组预紧过程，只需模拟表中的3种情况，并据此计算出4个参数α、β、δ和γ，将这4个参数根据实际的预紧顺序填入矩阵A中即可。

表1 参数计算方法

2 预紧力优化

2.1 有限元模型的建立

建立图2所示的法兰螺栓连接有限元模型，法兰材料为钢，弹性模量为2×105MPa，泊松比为0.3；螺栓材料为35CrMoA，弹性模量为2.03×105MPa，泊松比为0.3。法兰与螺栓间及上、下法兰间的接触都采用摩擦接触，其摩擦因数为0.2。对下法兰的下端面施加固定约束。

图1 有限元模型

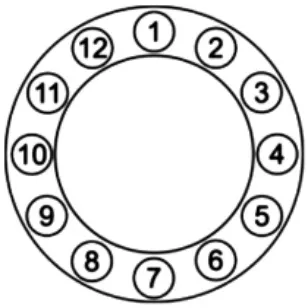
图2 螺栓编号

何联格等[10]的研究表明，采用交叉预紧能够使螺栓的残余预紧力更加均匀。为了研究无垫片多螺栓法兰连接预紧力分布规律和四参数法的准确性及特点，螺栓预紧过程采用两种交叉预紧顺序（如图2）：顺序①：1-7-4-10-2-8-5-11-3-9-6-12；顺序②：1-7-2-8-3-9-4-10-5-11-6-12。

2.2 结果分析

表2给出了使用四参数法计算的参数α、β、δ和γ。

表2 参数值

表3为根据顺序①列出的矩阵A，行代表预紧顺序，列代表该螺栓对已预紧螺栓的影响。以第一行为例，该行代表螺栓1预紧后，后预紧螺栓对其影响；当仅预紧螺栓1时，螺栓1未受其他螺栓影响，所以1号螺栓处为1；预紧螺栓2时，螺栓1仅受螺栓2影响，所以螺栓2处为α；预紧螺栓11时，螺栓12未预紧，所以螺栓11处为γ；预紧螺栓3时，螺栓1、2已预紧，所以螺栓3处为δ；预紧螺栓12时，螺栓1、2已预紧，所以螺栓12处为β；其余位置均为0。

表3 矩阵A

因此可以说，任意法兰螺栓连接都可以计算得到一个矩阵A，不同预紧顺序的参数在矩阵A中占据不同的位置。

以50 000 N为目标预紧力，计算两种预紧顺序下螺栓预紧力优化前和经四参数法优化后的预紧力分布情况。计算结果如图4所示，给出了螺栓组按顺序①和顺序②两种不同预紧顺序预紧下的各螺栓预紧力分布情况。

从图3可以看出，优化前在两种顺序下，由于弹性相互作用的存在，残余预紧力分散程度比较大，即残余预紧力分布不均匀。值得注意的是，一些螺栓的残余预紧力处于相似水平，顺序①下，12颗螺栓每4颗为一组，1号、4号、7号和10号螺栓预紧力损失最大，2号、5号、8号和11号螺栓次之，3号、6号、9号和12号螺栓预紧力损失最小；顺序②下，1号和7号螺栓预紧力损失最大，6号和12号螺栓预紧力损失最小，其余螺栓处于居中的相似水平。这意味着在无垫片法兰螺栓连接中，预紧力的损失多是由相邻螺栓引起的，弹性相互作用的影响会随着螺栓距离的增大而减小，也表明四参数法会有很好的适用性。

图3 预紧力仿真结果

经四参数法预紧力优化后，两种顺序下，各螺栓残余预紧力变得较为集中，分散性明显减小。但是，顺序①下，预紧力损失最大的1号、4号、7号和10号螺栓在经四参数法预紧力优化后，残余预紧力超过了目标预紧力；顺序②下，在优化前预紧力损失最大的1号和7号螺栓，经四参数法预紧力优化后残余预紧力也超过了目标预紧力，这表明该方法的准确性还有待提高。

表4给出了不同预紧顺序下对应的螺栓平均残余预紧力和残余残余预紧力标准差。对比图4和表4可以看出，优化前，预紧顺序①下螺栓的平均残余预紧力稍大，但是残余预紧力的标准差也大，即残余预紧力分布不均匀；经四参数法预紧力优化后，两种顺序下平均残余预紧力都大于目标预紧力，且残余预紧力标准差明显减小，预紧顺序①下的平均残余预紧力及残余预紧力标准差依旧大于预紧顺序②。

图4 预紧力仿真结果

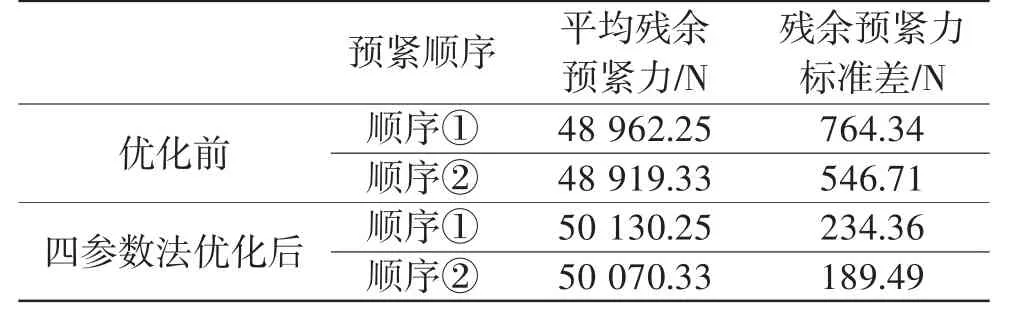
表4 平均残余预紧力及预紧力标准差

3 改进四参数法

3.1 矩阵A参数计算方法的改进

上文说明了四参数法的基本原理、矩阵A中参数的计算方法和矩阵A的列出方法，并分析了优化后的螺栓平均残余预紧力和残余预紧力标准差，比优化前有了很大的提升，但是个别螺栓残余预紧力依旧有较大分散性，原方法并未将螺栓b和c预紧的先后顺序考虑在内，因为螺栓在装配过程中是按照一定顺序逐个预紧的，那么在预紧过程中一定会出现螺栓b先于螺栓c 预紧，或者螺栓c先于螺栓b预紧，进而导致参数β和δ出现两种情况，如表5所示。

表5 参数β和δ两种数值

从表5可以看出，由于螺栓b和c预紧先后顺序的不同，导致参数β和δ分别出现了两种数值，且相差较大。基于此，表6给出了改进后的参数计算方法，其中参数α和γ的计算方法与上文相同，此处不再表述。

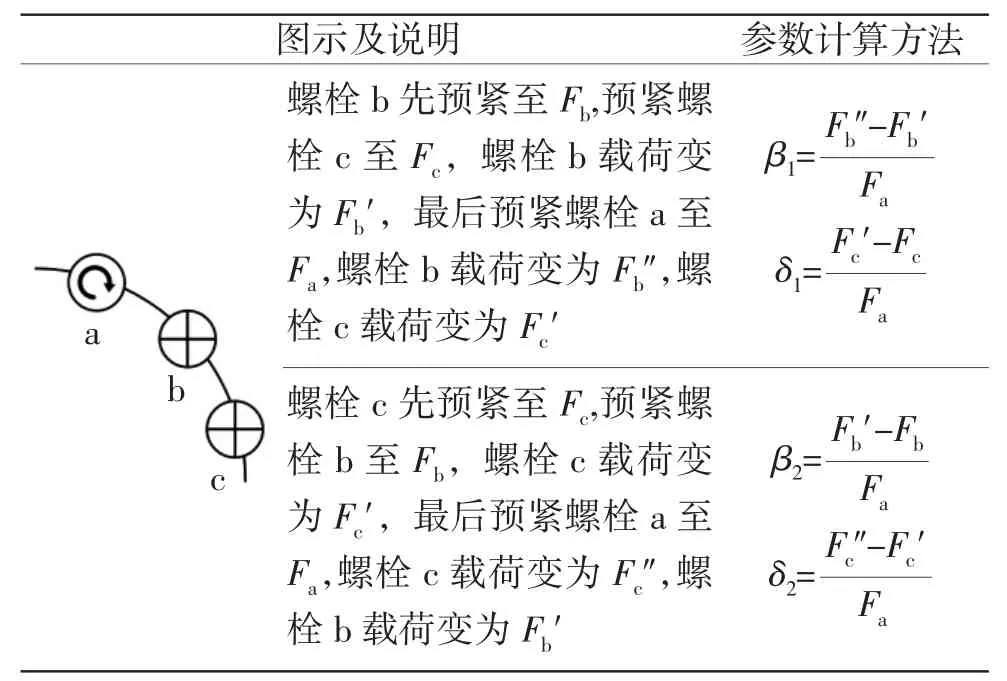
表6 参数计算方法的改进

3.2 结果分析

经改进四参数法计算出的参数及矩阵参考表2、表5和表3，此处不再赘述。

图4给出了两种预紧顺序下的各螺栓预紧力分布情况。经改进四参数法优化后的螺栓残余预紧力分布更加均匀，原本经四参数法优化后残余预紧力大于目标预紧力的螺栓（即顺序①中的1号、4号、7号和10号螺栓，顺序②中的1号和7号螺栓），在经改进四参数法优化后更加接近目标预紧力，各螺栓的残余预紧力分散程度进一步缩小。

表7给出了两种顺序下经改进四参数法优化后对应的螺栓平均残余预紧力和残余预紧力标准差。相对于四参数法，平均残余预紧力更加接近目标预紧力，残余预紧力标准差明显减小，预紧顺序①下，标准差减小了63%，预紧顺序②下，标准差减小了59%。

表7 平均残余预紧力及预紧力标准差

4 预紧顺序及预紧力大小对结果的影响

为研究预紧顺序和预紧力对结果的影响，采用顺时针顺序预紧（参考图2）（即：1-2-3-4-5-6-7-8-9-10-11-12）和3种预紧力（即：10 000 N、30 000 N和50 000 N）进行计算，计算出的参数值如表8所示，对比表2和表5，3种预紧力下的参数值基本相等，这意味着同一个法兰螺栓连接，预紧力的大小并不影响参数值的大小。

表8 参数值

图6给出了顺时针预紧顺序下3种预紧力经修正四参数法优化后的仿真结果，可以看出，随着目标预紧力的增大，残余预紧力的分散程度明显变大；对比图5的顺序①和顺序②，目标预紧力50 000 N下，顺时针顺序的残余预紧力分散程度明显最小。

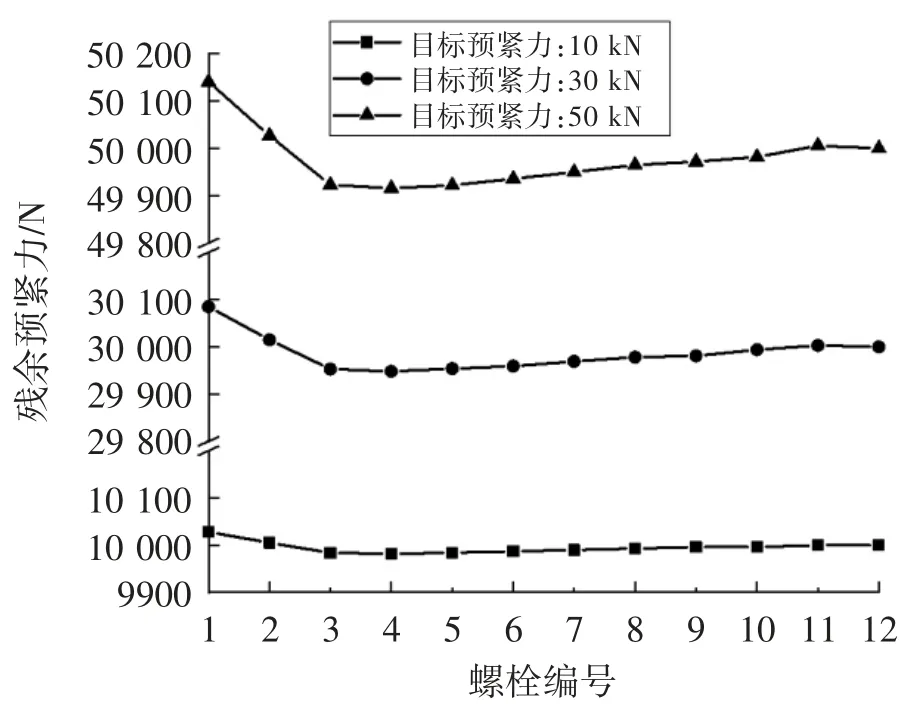
图5 预紧力仿真结果

表9给出了顺时针顺序下3种平均残余预紧力及残余预紧力标准差，平均残余预紧力均小于目标预紧力，残余预紧力标准差随着目标预紧力的增大而增大，即残余预紧力分布越不均；对比表7，顺时针顺序下的标准差最小，顺序②下的平均残余预紧力最接近目标预紧力。

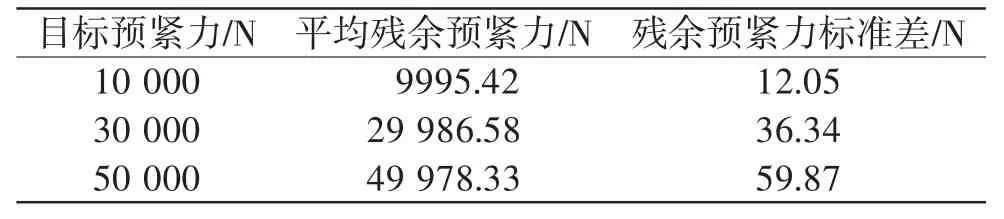
表9 平均残余预紧力及残余预紧力标准差

5 结论

1）基于四参数法对无垫片法兰螺栓连接进行预紧力优化，优化后的平均残余预紧力和残余预紧力标准差相对于优化前都有较大提升；对四参数法进行改进，改进后的四参数法使平均残余预紧力更加接近目标预紧力，标准差进一步缩小。

2）分析比较了预紧力和预紧顺序对优化结果的影响。顺时针顺序下，不同预紧力计算出的矩阵A参数值是相同的，但是残余预紧力标准差会随着预紧力的增大而增大；在3种顺序下，顺时针顺序下的标准差最小，顺序②下的平均残余预紧力最接近目标预紧力。