霍尔推进系统放电特性的数值模拟研究

李梦蝶,郑雨松,张婉婷,李志心,汪友梅

(杭州电子科技大学理学院,浙江 杭州 310018)

0 引 言

霍尔推进器,是现在最具代表性的电推进技术类型之一,它具有体积小、推力密度高且没有空间电荷限流等特点,在航天推进领域得到广泛应用[1-3]。自从1972年搭载前苏联“流星号”卫星实现首次试飞成功以来[4],霍尔推进器的研究一直在不断的进步中,整体来看,欧美发达国家、俄罗斯和日本的研发处于世界领先地位,如俄罗斯推出了先进的ATON型霍尔推进器[5]以及最高功率达20 KW的高功率霍尔推进器SPT-290[6]。美国也利用数值模拟方法在理论仿真上对霍尔推进器研究出很多结果,在高比冲方面有了很大的提升[7-8]。相较这些国家来说,我国有关霍尔推进器方面的研究比较晚,但经过多年的努力,我国在2020年自主研发了20 KW级大功率霍尔推进器,并取得点火试验的圆满成功[9],之后又于2021年成功研制出50-100 KW级大功率霍尔推力器,实现稳定点火运行,现在我国已经加速向国际水平靠近[10]。

霍尔推进器是一种典型电推进器,其结构如图1所示。霍尔推进器是由呈圆柱形轴对称结构的阳极和空心细长圆柱型的阴极电子枪等构成,而阳极是由基座、内外励磁线圈、内外磁屏蔽和放电通道组成。

推进工质从阳极底部进入放电通道,阴极发射电子。从阴极发射的电子,一部分会进入放电通道,并在通道口附近被磁场捕获。在磁场力的作用下,被捕获的电子将在径向磁场和轴向电场的作用下沿角向作漂移运动,形成霍尔电流。从阳极运动过来的推进工质分子与出口附近被捕获的电子流产生碰撞,发生电离。离子在轴向电场的作用下,将被高速推出放电通道,从而对推进器产生推力,为航天器提供所需的动力。

霍尔推进系统放电效率和稳定性是影响推进系统的推力和效率的主要因素。因此研究霍尔推进系统放电通道的性质也是科学家们研究的热点问题。哈工大于教授团队也自主研发了PIC数值模拟计算平台来进行磁场强度对磁极腐蚀等霍尔推进器的数值研究[11];大连理工刘教授团队利用等离子体综合流体模拟平台,研究了背景磁场对霍尔推力器等离子体特征的影响等。目前,有关霍尔推进器数值模拟的仿真研究主要有粒子模拟(PIC)和流体模拟两种模拟方法。流体模拟方法的原理是通过求解基于Maxwell方程组所建立的磁流体力学(MHD)方程,粒子模拟方法是通过计算机跟踪大量单个微观粒子。但由于流体模拟的过程不考虑各粒子的速度分布函数,导致流体模拟方法不能真实还原等离子体内部的微观不稳定性[12],所以本文采用粒子模拟方法。为此,本课题组历时4年成功自主开发了基于PIC-MCC算法的功能模块化的数值模拟平台(HD-HER),实现了霍尔推进系统整个放电过程的动态模拟。本文是通过HD-HER平台模拟计算了霍尔推进器通道中等离子体的输运性质及推力。

1 模型与方法

1.1 理论模型

霍尔推进系统放电通道内粒子的运动通过电磁场来驱动,满足牛顿运动方程:

(1)

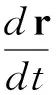
(2)

式中,v为带电粒子的速度,m为带电粒子的质量,E,B为作用在带电粒子上的电磁场,r为带电粒子的位移,dt为时间步长。

通过Boris旋动法[13]对方程(1)、(2)进行求解,即可得到粒子的运动规律。因为通道中有电子,中性原子,离子三种粒子,在运动过程中会产生碰撞,所以我们采用蒙特卡罗碰撞方法(MCC)[14]来处理粒子之间的碰撞过程[15],本文为了简化模型,只考虑电子和中性粒子之间的电离碰撞。

方程(1)中,电磁场通过麦克斯韦方程组来进行求解:

(3)

(4)

·B=0

(5)

×B=μ0J

(6)

而在霍尔推进器内部通道中,等离子体产生的磁场远远小于外加磁场,所以:

(7)

上式中B是磁感应强度,E为电场强度,μ0为真空磁导率,J为电流,ρ为电荷密度,ε0为真空介电常数。

在求解此方程的过程中常用磁势A和电势φ作为数值计算的变量:

2A=-μ0J

(8)

(9)

在柱坐标系下展开即:

(10)

(11)

这样能更好地构造出泊松方程,将问题简单化,把求解场的问题转化为求解势的问题,再利用有限差分法解出泊松方程,并进行程序运算即可得到每个网格节点对应的电磁场。电磁场对其中的电荷产生电磁力,从而推动粒子的运动,改变粒子在空间的密度分布。本文采用PIC-MCC算法,具体流程如图2所示:

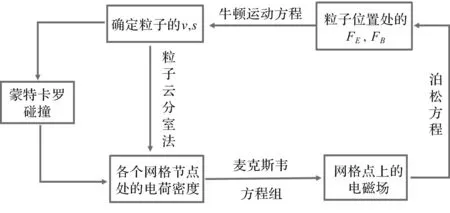
图2 PIC-MCC方法的流程图

1.2 初始条件和边界条件

本文研究的是推进系统放电通道和羽流区粒子的运动,推进工质是氙气,模拟计算的区域为整个放电通道和羽流区域。涉及各物理量的初始值如表1所示。

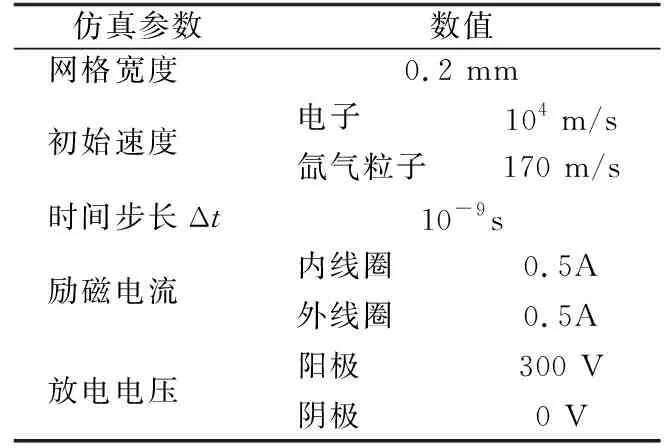
表1 模拟中所给初始物理量

对于仿真中遇到的边界,根据霍尔推进器阳极的轴对称结构,认为对称轴处磁势为0,无穷远处磁势为0。

2 结果与讨论

2.1 电磁场的分布

本文通过设定内外励磁线圈电流,得到电流都为0.5 A时对应的磁场分布,该分布中选取了通道内部的磁场分布,即轴向坐标为3-60 mm,径向坐标为11.5-21.5 mm(轴向坐标零点和径向坐标零点均为基座处底部,基座的厚度是3 mm)。如图3所示,发现径向磁场分布呈现先增加后减小的变化规律,通道口附近磁场是最大的,并且分布均匀,这样的分布会使得电子从阴极发射后,能够在通道口强径向磁场的作用下被捕获。捕获的电子越多,氙气分子与电子碰撞的概率就越大,电离率也就越高。而通道内部磁场很小,几乎为0,使得电子不会被约束,这样就能够降低由于电子向壁面偏转、撞击而造成的壁面腐蚀,可以提高霍尔推进器的寿命。

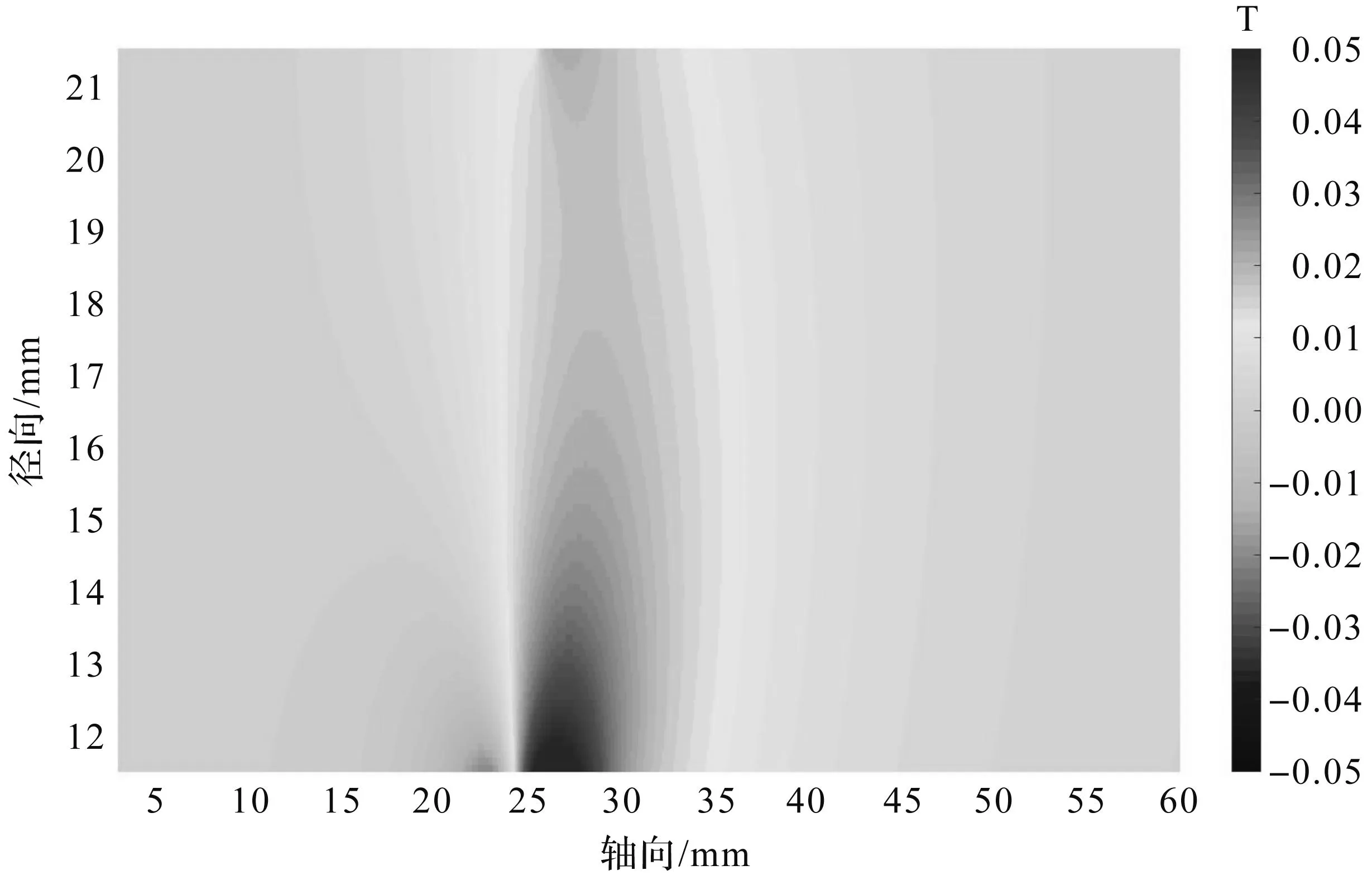
图3 径向磁场分布

虽然对于通道内部粒子来说起主要作用的是径向磁场,但轴向磁场的分布也会对粒子有影响。轴向磁场的分布如图4所示,可以看到依旧是通道口附近的磁场值最大。

图4 轴向磁场分布

放电通道中轴向静电场的分布,如图5所示。可以观察到通道口附近的电场强度最大,因为霍尔推进器的电场是由阳极和阴极的电势差而产生,所以放电通道内部可以看成一个挖空的等势体内部,因此造成了通道内部电场很小,阴极附近最大的趋势。图6为轴向电场放电通道中心轴线的电场强度分布。

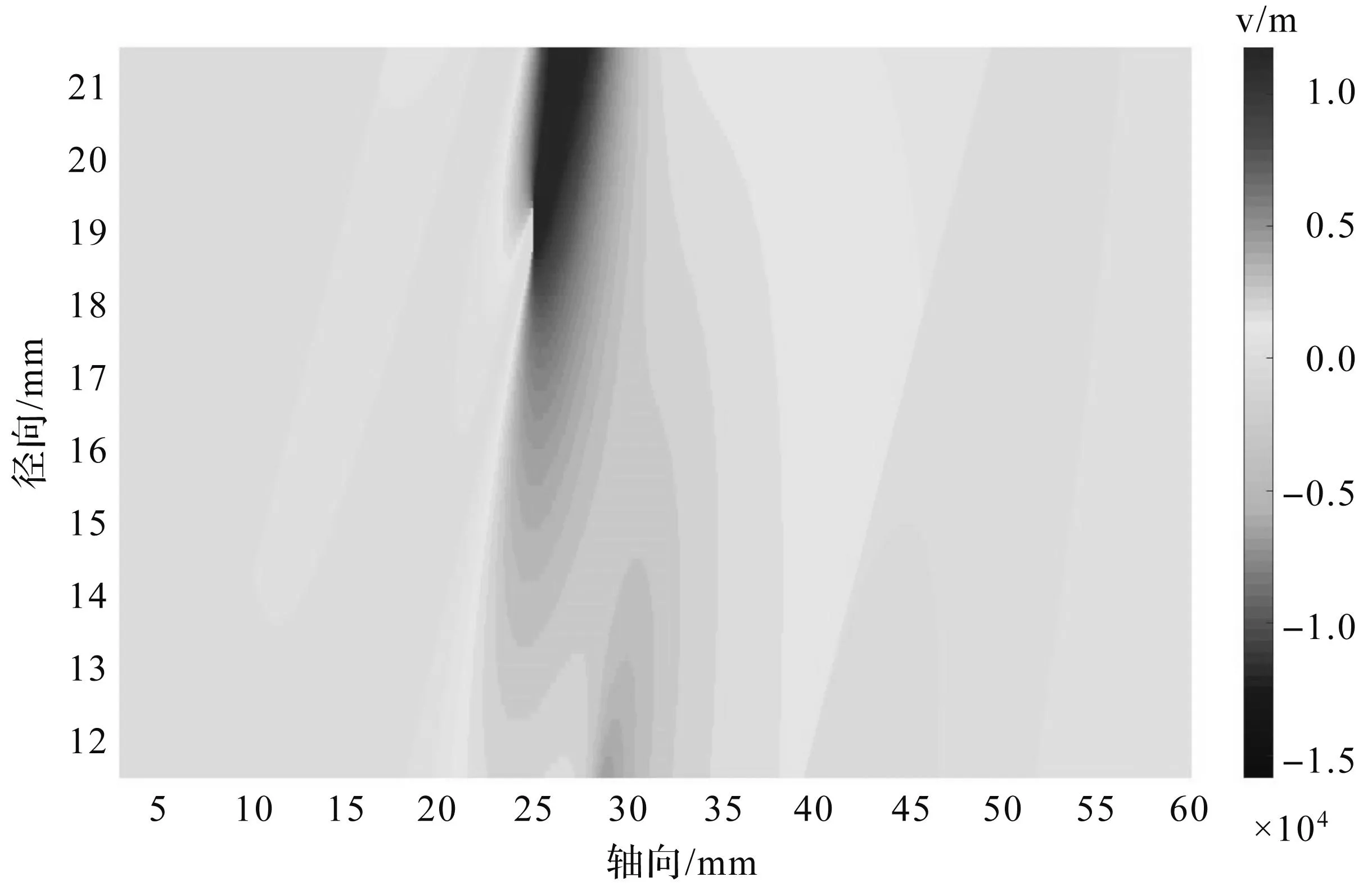
图5 轴向静电场分布

图6 轴向电场的中轴线上电场分布

2.2 等离子体密度分布

霍尔推进器的放电过程是先由电子和中性原子的碰撞电离出离子,之后离子在轴向电场的加速下喷出产生推力,所以本文在上述电磁场的基础上模拟了电子和离子在稳态情况下的密度分布,但由于所模拟粒子较多,为了减少模拟时间,本文中以每个粒子代表107个和它运动状态完全相同的粒子,如图7所示为放电过程中的电子数密度分布。从图7可以看到电子从阴极发射后,一部分电子被通道口处的磁场捕获做霍尔漂移运动,一部分在电场力的作用下,向阳极漂移。通道内部磁场的值较小,电子在放电通道内部与壁的碰撞概率较小。由于通道口附近很强的径向磁场作用,随着时间的增加,在通道口附近被磁场捕获的电子越来越多,形成一个高密度电子区域。随着放电时间的推移,高密度电子区域逐渐稳定,推力器到达稳定放电状态,如图7(a)-(d)所示。此时出口电子的密度最高处达到8.9×1011m-3(对应真实粒子密度为8.9×1018m-3)。

图7 放电过程中不同时刻通道内的电子密度分布

图8为在稳定放电时,各轴线(r=13 mm,r=16 mm,r=19 mm,其中r=16 mm为放电通道中心轴线)上电子密度的分布情况。从图8中可以看出,从阳极开始向通道中,电子数密度是呈现先缓慢变化待到通道口时快速增大,之后再快速减小的趋势,并且中轴线r=19 mm时电子数密度是最大的,而轴线r=13 mm的电子数密度是远小于其它两个轴线上的值,这是因为电子阴极靠近r=19 mm处,所以电子一出来就会被磁场所捕获。因此可以看出不同轴线上电子的密度分布有所不同。

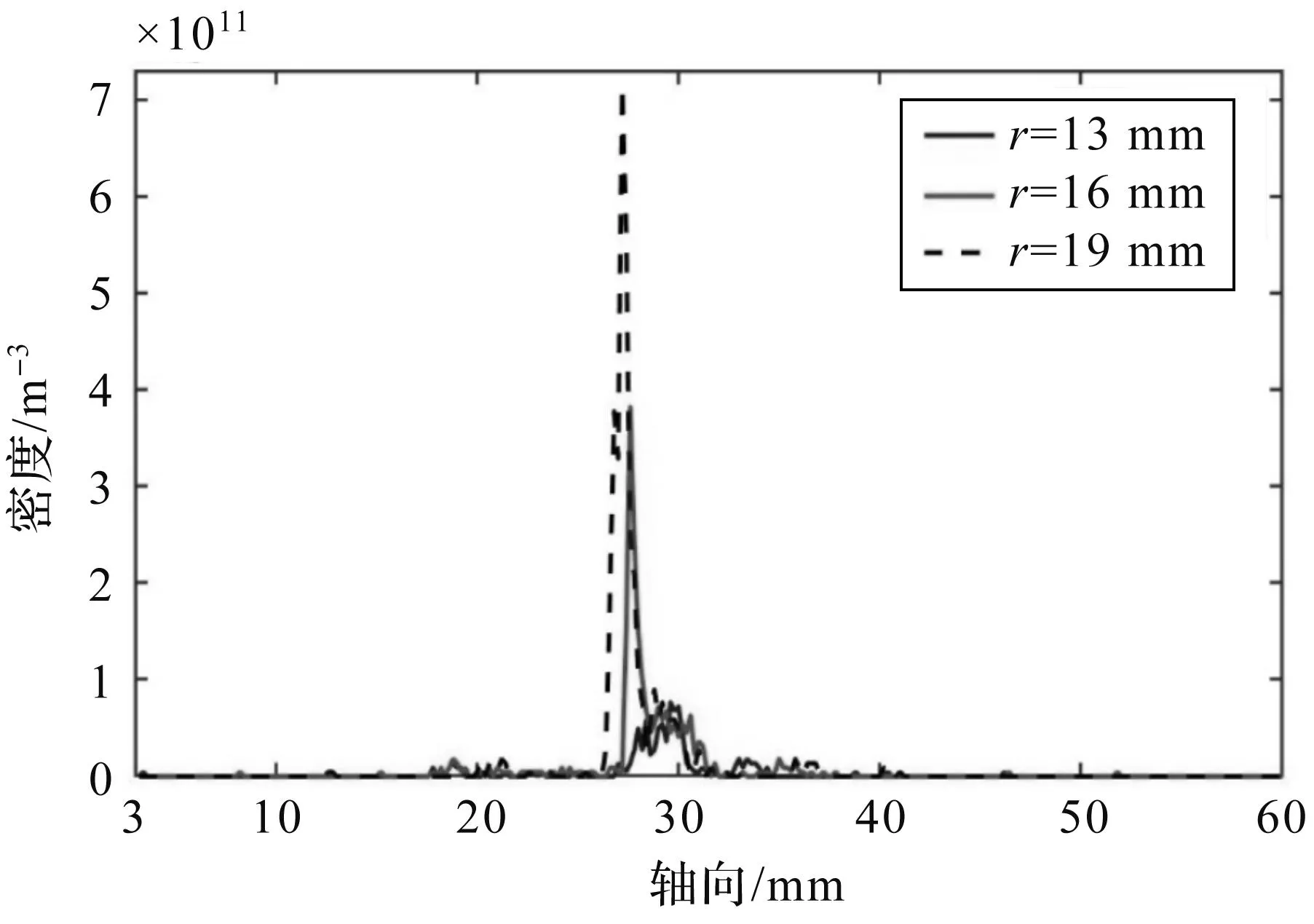
图8 电子在放电通道中轴向的密度分布

由于电场和磁场的共同作用,会使阴极发射的电子和中性气体发生电离碰撞,从而产生离子和新的电子,所以离子的密度分布更能体现放电的过程。如图9所示为放电过程中不同时刻的离子密度分布图。从图9可以看出,离子的分布和电子数密度分布并不完全相同。在放电初期,离子大多在通道内部,这是因为虽然电子在通道内部没有大量停留,但在运动过程中和阳极注入的中性气体会发生碰撞,从而使中性气体分子电离。由此产生的离子质量相比电子较大,同时受磁场约束也较小,所以并没有快速的跑出通道。由于通道内部的电子数较少,没有发生碰撞的中性气体分子将会继续向前运动,与通道口附近的高密度电子束发生电离碰撞。随着时间步长的增加,在通道口附近(高电子数密度处)形成高离子密度区。这些离子在轴向电场的作用下,加速向通道外运动,形成羽流。此时通道口的密度高达5.7×1011m-3(对应真实粒子密度为5.7×1018m-3)。图10是放电通道轴线上离子密度的分布情况。从图10中可以清楚可以看到离子在轴向上的分布情况,在通道口附近的离子密度是最大的。

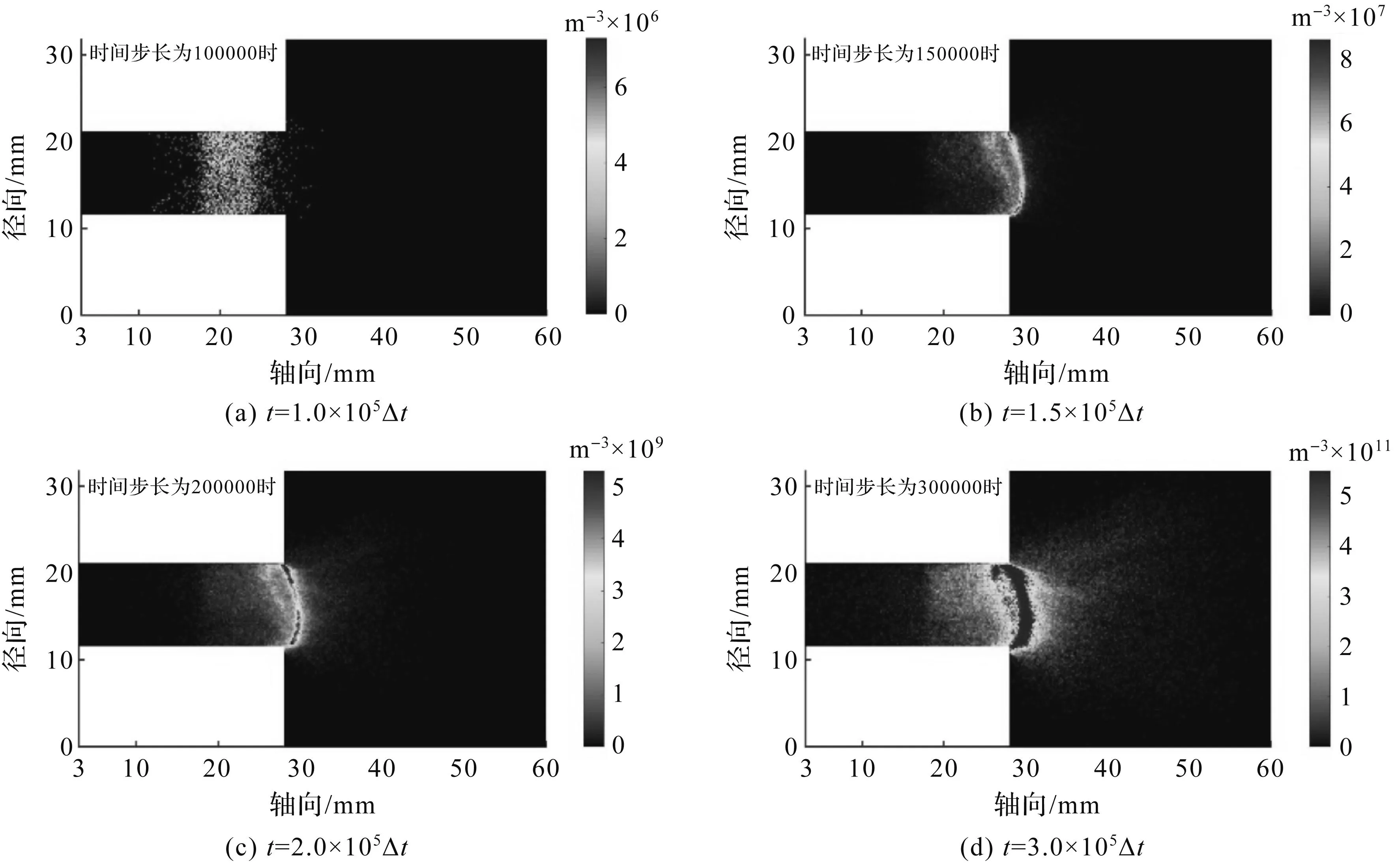
图9 放电过程中不同时刻通道内的离子密度分布

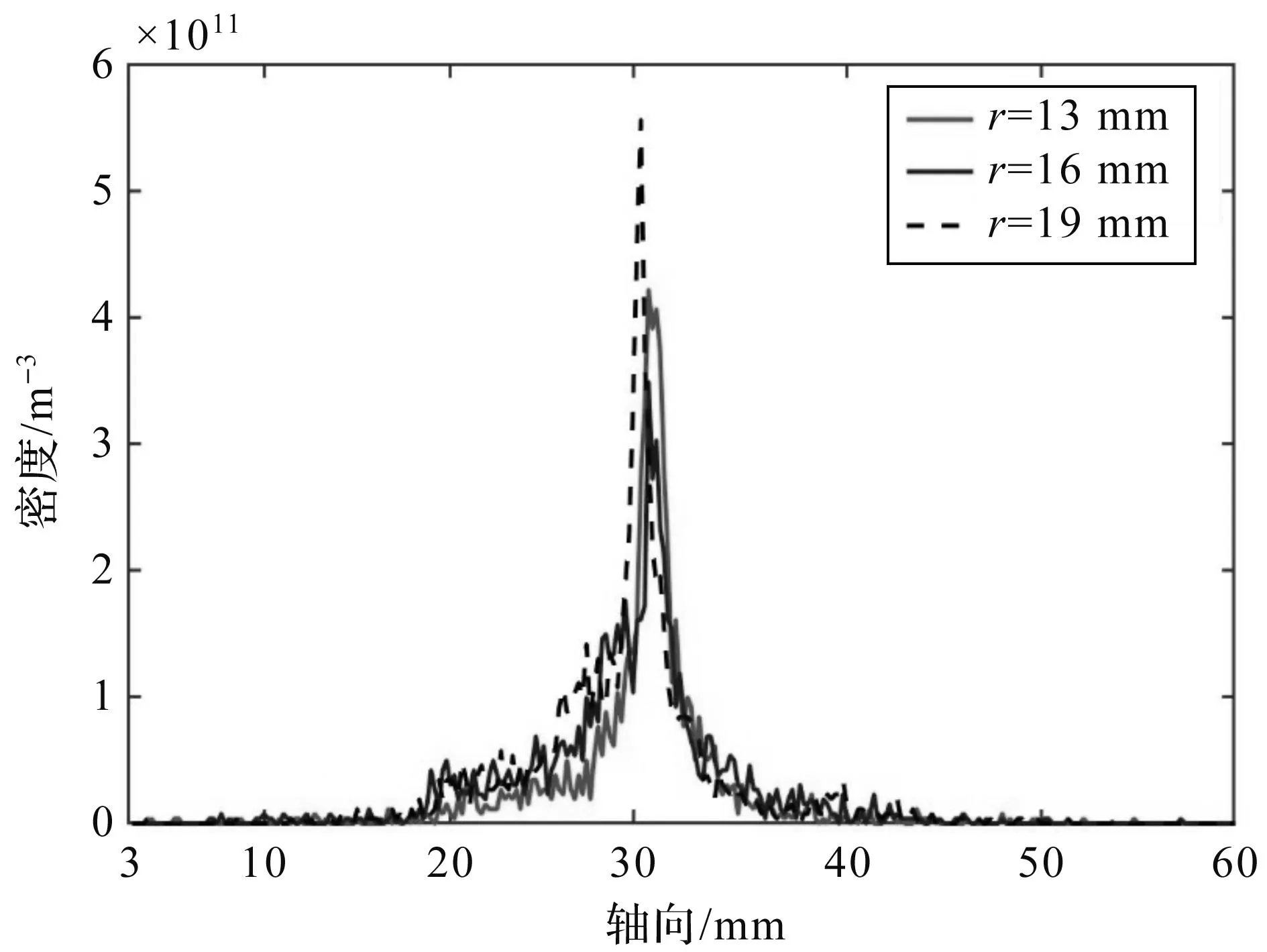
图10 离子在放电通道中轴向的密度分布

2.3 离子速度和推力

如图11为离子在轴向上的速度分布。在此图中,离子在通道口速度最小,这是因为在此处开始电离得到大量的离子,离子数目很多,并且还没经过电场加速。电离之后,离子在轴向电场的作用下,快速加速,在很短的时间内离子获得较大速度,离开放电通道。之后又因为电场的分布关系,速度有所减弱,利用此数据经过霍尔推进器的推力公式可以算出中轴线r=16 mm时通道口离子的推力约为8.09 mN,和南洋理工大学PSAC实验室测量的结果进行对比,发现计算模拟的结果和实验结果吻合得比较好[16]。

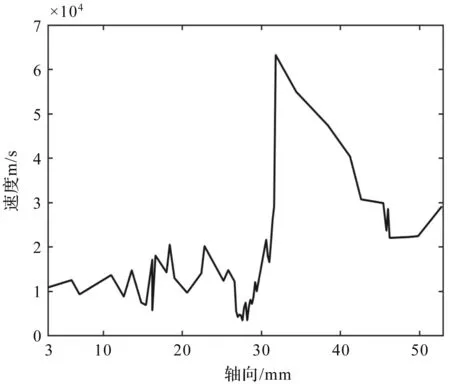
图11 离子在轴向上的速度分布

3 结束语

本文通过课题组自主开发的HD-HER平台模拟计算了霍尔推进器放电性质,得到放电过程中电子和离子密度的动态分布。并得到工质质量流0.4 mg/s时推进系统的推力,这个结果与PSAC的实验基本吻合。这也进一步说明本团队所开发的HD-HER平台模拟的准确性。该研究结果将为后续推进器的结构优化和效率提升提供前期的理论支持,对更为复杂的微推进系统发展具有十分重要的理论指导意义。