决策系统化分析在工程中的应用

解倩　闯超

摘 要：文章通过具体的实际案例详细说明了决策分析如何运用在工程中，论证了决策分析的特点是要用定量的方法处理决策者的价值判断，它是自然科学与社会科学的交叉，它所采取的研究方法既不同于纯自然科学，也有别于传统的社会科学，它综合了管理学、统计学、运筹学、系统科学等各科知识和理论。

关键词：决策 系统化 分析

1 前言

制定决策并承担相应的责任是管理人员的基本工作之一。当代著名管理学家西蒙教授说“管理就是决策”，这一精辟论断突出了决策在现代化管理中的核心地位。自然科学研究的是客观世界，是客观世界中的事实元素，采用的方法以定量为主，而社会科学主要研究由人组成的时候、社会中的人及人际关系，其核心是价值元素，使用的方法以定性为主。而决策分析的特点则是要用定量的方法处理决策者的价值判断，它是自然科学与社会科学的交叉；它所采取的研究方法既不同于纯自然科学，也有别于传统的社会科学，它综合了管理学、统计学、运筹学、系统科学等各科知识和理论[1-3]。

2 应用

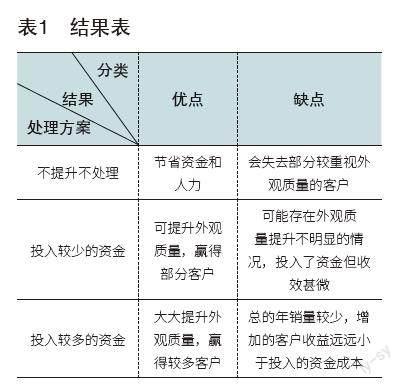
公司新开发车型试生产过程中发现，车身侧围局部有肉眼不可见但专业检测可见的轻微凹坑现象，而对外观质量的要求取决于每个客户的主观感受，部分客户会注重车辆外观质量，而部分客户则更重视车辆的使用性能。所以，是否要投入人力资源和资金去改善这个现象以提升整车的外观品质，以及如若需要改善应采取何种方案，公司经过分析得出以下结果表１：

公司项目组开展了前期的调查工作。首先，按照市场对该款车外观品质提升的预期需求，按照提升品质投入资金100万，得出其预期收益，见表2：

由不确定型决策的定義及其应满足的条件可知，该问题属于不确定型决策问题。由于乐观准则和悲观准则都过于极端，因此我们分别选择折中决策准则和后悔值准则对该问题进行分析。

取乐观系数为0.55，采用折中决策准则进行分析，得出结果如表3：

由表3可知，运用折中决策准则，应该选择投入资金以提升外观品质。

而由于折中决策原则的乐观系数确定存在较大的主观性，而且对中需求的这一信息没有加以利用，导致信息利用的不够充分，所以，再使用后悔值准则对该问题进行进一步的分析，以期避免较大的决策失误，得到一个更加合理的结果。

运用后悔值决策准则，分析结果如表4所示：

由表4可得，运用后悔值决策准则，也应选择投入资金以提升外观品质的方案。

故，公司最终决定，投入资金以提升该车型的外观品质，确定投入项目资金控制在100万元以内。

以上分析结果为，对该外观品质进行立项提升。关于提升方案，现有两个方向，一是后期补救，即逐台检测，有问题则进行修复，该方向外观品质提升成功率为0.6；二是从源头入手，即设计变更，从造型、成型工艺、结构设计等方面进行优化，该方向外观品质提升成功率为0.8。而每个方向的方案成功与否以及与该车型不同销量情况下的盈亏情况（单位：万元）见表5所示：

针对该决策的选择，我们选用的画决策树的方法进行分析，因为决策树是对决策局面的一种图解，也是风险型决策中常用的方法。用决策树可以使决策问题形象化，它把各种备选方案、可能出现的自然状态以及各种损益值简明地绘制在一张图表上，便于我们审度决策局面，分析决策过程，使整个过程简单明了。该问题的决策树绘制见图1：

由此决策树可知，选择前期设计变更提升外观品质为更优的解决方案。

项目组对于影响该外观品质问题（侧围轻微凹坑）的各个因素进行了研讨，分析一致认为产品减薄率偏低，整体刚性不足，涂装受热后应力不均是引起变形的主要原因，并随之制订了三套前期设变方案，分别如下：

H1修改造型

H2增加零件料厚

H3增加支撑件及膨胀胶

根据前期多个项目经验，各个方案所能提升该车型外观的品质对销量的影响见下表，其中，先验概率为p（θ1畅销）=0.4，p（θ2一般）=0.4，p（θ3滞销）=0.2。

相对销售情况，每个方案所带来的盈利值见表6：

现在想对各个方案的预期效果及销量进行更精准的评估，需要对各个方案先进行CAE分析，进行分析所需要的费用为30万元，其似然函数表如表7所示：

由此可知，该车型销售预测情况有三种，即θ1（畅销），θ2（一般），θ3（滞销），可采取的实施方案也有三种，即H1，H2，H3。利用贝叶斯决策分析相关知识，于是得

无补充信息期望收益

=-200×0.4＋50×0.4＋（-100）×0.2=80（万元）

=-150×0.4＋100×0.4＋（-50）×0.2=90（万元）

=-180×0.4＋50×0.4＋（-20）×0.2=88（万元）

由风险型决策的期望值准则得到目前最满意方案：无论该车型市场销量如何，提升方案H2为最佳方案，最大期望盈利值为90万元。

接着我们要对是否先做CAE分析再确定最优方案进行决策计算，首先要计算CAE分析后的各个期望值，必须先计算全概率和后验概率（=）。根据全概率公式，有

计算结果如表8所示。

利用贝叶斯公式计算后验概率，有

相关计算结果如表9所示。

（1）当分析结果为采用方案H1时：

1200×0.5714+50×0.3810

+（-100）×0.0476=128.57

150×0.5714+100×0.3810

+（-50）×0.0476=121.43

180×0.5714+50×0.3810

+（-20）×0.0476=120.95

最大期望收益值 max{128.57，121.43，120.95}=128.57

（2）当分析结果为采用方案H2时：

1=200×0.5263+50×0.4211+（-100）×0.0526=121.05

=150×0.5263+100×0.4211+（-50）×0.0526=118.42

=180×0.5263+50×0.4211+

（-20）×0.0526=114.74

最大期望收益值 max｛121.05，118.42，114.74｝=121.05

（3）当分析结果为采用方案H3时：

1=200×0.4444+50×0.4444+（-100）×0.1111=100

=150×0.4444+100×0.4444

+（-50）×0.1111=105.56

=180×0.4444+50×0.4444

+（-20）×0.1111=100

最大期望收益值 max{100，105.56，100}=105.56

該决策问题经过CAE分析后所得到的期望收益值为：

E3=128.57×0.42+121.05×0.38+105.56×0.36=138

根据补充信息价值定义，EVAI=不完全信息期望收益-无补充信息期望收益，

可得EVAI=138-90=48万元>20万元

所以，我们是值得花费20万元先进行CAE分析的，根据CAE分析结果确定最优方案。

3 思考

由此可见，在工作中运用系统分析法做决策，会让我们处理问题更加科学和高效，避免一些无用的工作或者错过最佳解决方法。决策分析的理论和方法，不仅仅在我们的工作中体现其重要性和优越性，小到日常生活的琐碎，大到政府国家的方针政策，都离不开系统分析决策的思路的运用，我们只有深刻理解并熟练掌握，才能使这个科学的方法真正地为我所用。

当然，任何事物都有其两面性，我们也不能忽略问题本身的价值，而一味地追求最优的解决方案，这样也可能使我们付出远高于问题本身价值的更高的代价，或者暂用了大量的时间和精力而错失了最佳时机，被别人抢占了先机。时间、价值、效率等都是我们要综合衡量的因素。

总之，利剑在手，如何运用，还需要大家各显神通。

参考文献：

[1]陶厂琪. 决策理论与方法[M].北京：高等教育出版社，2017.

[2]岳超源. 决策理论与方法[M].北京：科学出版社，2012.

[3]简祯富. 决策分析与管理[M].北京：清华大学出版社，2019.