圆锥体全局角度尺寸评定方法

赵新宇, 赵则祥, 李 彬, 任东旭, 席建普

(1.中原工学院 计算机学院，河南 郑州 450007； 2.中原工学院 机电学院，河南 郑州 450007； 3.机械工业光学传感与测试技术重点实验室，河南 郑州 450007)

1 引 言

圆锥形要素是机械零(部)件中常用的要素之一,如刀柄和一些机床的尾部顶尖部件、锥形销、锥形滚子轴承、锥齿轮等均包含圆锥形要素。圆锥面的尺寸、角度规格及其公差和几何公差在国际标准化组织(ISO)、美国机械工程师学会(ASME)和我国的相关标准[1～3]中进行了规定,但标准一般是基于两点尺寸。为了提高圆锥面的质量,在测量和评定中使圆锥的角度尺寸更加明确,GB/T 38762.3规定了全局角度尺寸[4],在图样上需标注相应的附加符号。有关圆锥全局角度尺寸的测量和评定的文献目前尚未看到。与在圆柱体圆柱度误差和全局尺寸评定时确定参考圆柱的轴线参数一样,可以使用一些几何误差评定中所使用的优化算法来确定参考圆锥(最小二乘圆锥和最大最小圆锥)的轴线参数等,以评定圆锥的全局角度尺寸。许多学者利用优化算法对几何误差进行了评定,取得了较好的效果。董紫燕等[5]将改进后的差分进化算法与人工蜂群算法混合迭代优化,用于空间直线度误差的评定,提高了计算精度和收敛速度;孔玉强等[6]通过改进区域算法,提高了圆度误差的评定效率;干江红等[7]利用将外包络点压缩至常数范围等方式,提高了最小外接法圆度误差的评定效率;Liu W W等[8]将最小区域圆柱度误差评定模型的线性化处理与蒙特卡洛方法相结合,实现圆柱度误差最小区域法的评定;Yang Y等[9]采用改进和声搜索算法研究了圆柱度误差的评定问题;Liu F等[10]提出了适用于多测点的递推最小区域算法,具有快速、精确评定的特点;吴天昊等[11]采用海鸥优化算法对圆柱度误差进行了评定,并研究了该算法在评定应用中的相关问题;Zhao Z X等[12]将最速下降和BFGS-0.618综合算法、基因算法用于圆柱体全局尺寸的评定,并对两种优化算法的精度和效率进行了比较。

除了上述几何误差与全局尺寸评定用优化算法外,乌鸦搜索算法(crow search algorithm, CSA)、人工生态优化算法(artificial ecosystem-based optimization, AEO)、平衡优化器(equilibrium optimizer, EO)、飞蛾扑火优化算法(moth-flame optimization, MFO)等算法[13～17]均可用于圆锥全局角度尺寸的评定。本文基于圆周轮廓提取方案,开展圆锥全局角度尺寸的评定方法研究,建立圆锥全局角度尺寸的评定模型,在用上述部分优化算法对圆锥角度尺寸评定的基础上,综合考虑各优化算法的评定精度和效率,选用MFO作为圆锥全局角度尺寸评定的优化算法,研究该算法在圆锥全局尺寸评定应用中的相关问题。本文的研究将有助于GB/T 38762.3在机械制造业中的实施。

2 全局角度尺寸及其图样标注

图1 圆锥全局角度尺寸的图样标注Fig.1 Drawing indications of global angular sizes of cone

3 全局角度尺寸评定模型的建立

3.1 最小二乘全局角度尺寸的评定模型

根据全局角度尺寸的定义和测量仪器的功能,采用圆周法[18]作为圆锥(台)轮廓要素的提取方案,如图2所示,图中,EA为参考圆锥面的轴线。当用最小二乘法拟合参考圆锥面时,参考圆锥面即为最小二乘圆锥面,其轴线EA用LA表示,该轴线一端点OL1(或oLn1)在xOy平面上的x,y和z坐标分别为xL1(或xLn1),yL1(或yLn1)和0。

图2 圆周轮廓和参考圆锥面Fig.2 Roundness profiles and reference cone surface

图3是第i圆周轮廓及其参数的示意说明,参考圆实际上是参考椭圆,因为在圆锥面轮廓提取之前通常要对被测工件进行调心调平处理,因此,为简化建模,用参考圆代替参考椭圆。当用线性最小二乘法和非线性最小二乘法拟合最小二乘圆锥面时,图中参数下标E分别用L和Ln表示。eLi(或eLni)为第i参考圆的偏心量,其x,y和z的坐标为xLi=xL1+pLzi(或xLni=xLn1+pLnzi),yLi=yL1+qLzi(或yLni=yLn1+qLnzi)和zi,pL(或pLn)和qL(或qLn)的含义见文献[19],zi=(i-1)Δz,Δz为相邻圆周轮廓的z向距离。Pij为第i圆周轮廓上第j采样点到z轴(工作台回转轴线)的径向尺寸,rLij(或rLnij)为第i圆周轮廓上第j采样点到偏心点OLi(或OLni)的距离,RLi(或RLni)为参考圆的半径。

图3 第i圆周轮廓及其相关参数Fig.3 The ith roundness profile and its related parameters

根据最小二乘法的定义,最小二乘方程可表示为:

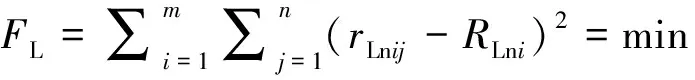
(1)

式中:m为提取的圆周轮廓数;n为每个圆周轮廓的采样点数;rLnij和RLni可表示为:

(2)

式中:RLn1是最小二乘圆锥面的大端半径;TLn是最小二乘圆锥面半角的正切;φj是第j采样点与x轴间的夹角,等于(j-1)Δφ,Δφ是每个提取轮廓上相邻采样点之间的夹角。由于式(1)是一个非线性最小二乘方程,待定参数xLn1,yLn1,pLn,qLn,RLn1和TLn可用优化算法确定上述参数和最小二乘全局角度尺寸。

在圆锥轮廓提取之前,对被测圆锥进行了调心和调平处理,偏心量eLni较小,因此,rLnij可简化为rLij,最小二乘圆锥面待定参数xLn1,yLn1,pLn,qLn,RLn1和TLn转化为待定参数xL1,yL1,pL,qL,RL1和TL,即

rLij≈Pij-(xLi+pLzi)cosφj-(yLi+qLzi)sinφj

(3)

将式(3)代入到式(1),非线性最小二乘问题变成线性最小二乘问题后,对6个待定参数xL1,yL1,pL,qL,RL1和TL分别求偏导,并分别等于0,整理后得到六元一次方程组,通过求解该线性方程组,得到待定参数xL1,yL1,pL,qL,RL1和TL。

参数TLn或TL确定后,可由式(4)确定圆锥面的最小二乘全局角度尺寸αLn或αL,单位:(°)。

(4)

3.2 最大最小全局角度尺寸的评定模型

当用最大最小法拟合参考圆锥面时,图1中的参考圆锥面即为最大最小圆锥面,其轴线EA用MA表示,该轴线一端点OM1在xOy平面上的x,y和z坐标分别为xM1,yM1和0。图2中的下标E均替换为M,表示是与最大最小圆锥面相关的参数。根据最大最小拟合法的定义,最大最小圆锥面方程可表示为:

(5)

式中:CM=[xM1yM1pMqMRM1TM];1≤i≤m;1≤j≤n;dMij可由式(6)计算得到。

dMij=[(Pijcosφj-xM1-pMzi)2+(Pijsinφj-yM1-qMzi)2]1/2-(RM1-TM×zi)

(6)

利用优化算法确定参数CM后,将式(4)中的下标L或Ln替换为M,即可作为最大最小全局角度尺寸的计算公式。

3.3 MFO在全局角度尺寸评定中的应用

全局角度尺寸的非线性最小二乘评定和最大最小全局角度尺寸的评定均可归类为最优化问题,可用优化算法搜索全局角度尺寸评定中圆锥相关参数CLn和CM,两者的优化函数分别见式(1)和式(5)。MFO是一种群智能算法,该算法的主要灵感来自于自然界中飞蛾被称为横向方向的导航方法。飞蛾在夜间通过相对于月球保持一个固定的角度来飞行,这是一种非常有效的长途直线飞行的机制。该优化算法具有程序编写简单,运算速度快,运算精度高等特点,有关该算法的原理和详细信息见文献[17]。本文给出了圆锥相关参数评定的MFO流程图,如图4所示,图中,符合度ft由式(1)和式(5)确定。式(1)用于非线性最小二乘全局角度尺寸评定中ft的计算;式(5)用于最大最小全局角度尺寸评定中ft的计算;E=Ln或M,用于全局角度尺寸的非线性最小二乘评定或最大最小全局角度尺寸评定。CM0或CLn0为搜索CM或CLn的初始值;f=[f1f2],其含义见式(11);lb和ub是2个1×6的行矢量,分别为搜索CM或CLn的下、上边界;bc为边界系数;N和T分别为种群数和最大迭代次数;rand为在区间(0,1)内生成的一个均匀分布随机数;～为逻辑非;ftS和CES分别是符合度ft从小到大排序后的符合度及其对应的CE;ftSB和CESB为迭代过程中设定的较优符合度及其对应的优化参数行向量;ftP和CEP分别等于上一次迭代得到的ftS和CES;ftPS为由符合度ftP和ftS合并形成的2×N维行向量;CEPS则由CEP和CES合并得到;火焰数F_No可由式(7)计算得到。

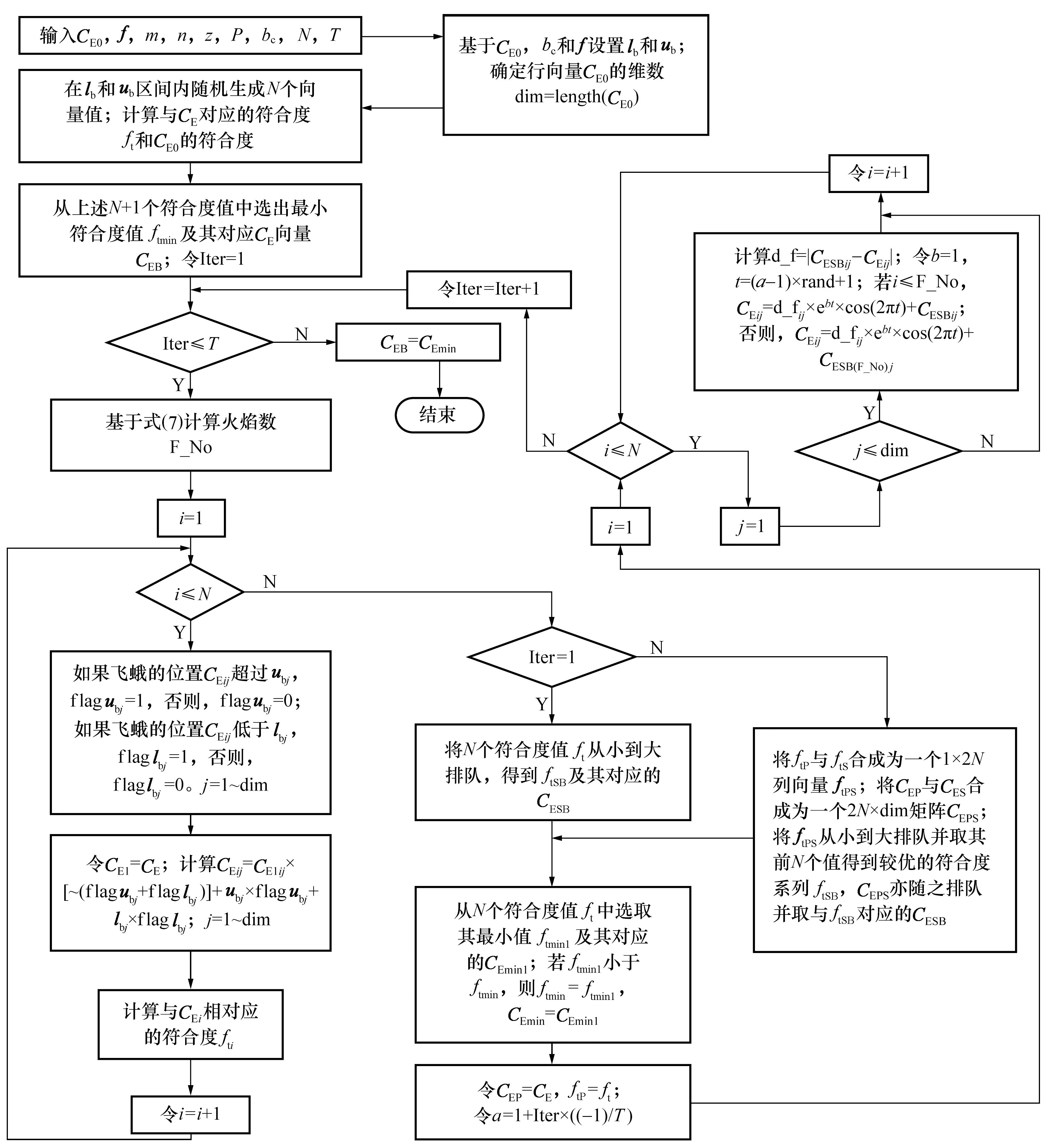
图4 圆锥全局角度尺寸评定用MFO流程图Fig.4 MFO flowchart used in the evaluation of cone’s global angular sizes

F_No=round(N-(Iter×((N-1)/T))

(7)

式中:round是将括号中计算得到的数值圆整到最近的整数;Iter为迭代次序。

4 实验与讨论

4.1 实验

基于圆周提取方案的4个圆锥仿真试样S-1、S-2、S-3和S-4的仿真过程如下:1)用Talyrond 585LT形状测量仪分别对4个圆柱按表1所示的m、n、Δz提取圆周轮廓。2)用标准圆柱消除圆周轮廓的径向系统误差,径向系统误差的消除方法见文献[20]; 4个圆柱消除径向系统误差后的圆周轮廓如图5所示(分别对应于4个圆锥仿真试样)。3)仿真圆锥试样上第i圆周第j采样点到形状测量仪回转工作台回转轴线(图1所示z轴)的径向尺寸Pij可表示为:

表1 4个圆锥仿真试样规格与轮廓提取参数Tab.1 Specifications and parameters of profiles’ extraction of four cone simulated samples

(8)

图5 4个圆柱圆周轮廓示意图Fig.5 Schematic of roundness profiles of four cylindrical samples

式中:PCij为消除径向系统误差后圆柱试样第i圆周轮廓第j采样点到形状测量仪回转工作台回转轴线的径向尺寸;zi为第i圆周轮廓与xOy平面间的z向距离;α为圆锥仿真试样的圆锥角的公称尺寸(见表1)。依据上述仿真原理和表1中的参数,由4个圆柱试样C-1、C-2、C-3和C-4的圆周轮廓分别获得了四个圆锥仿真试样S-1、S-2、S-3和S-4的圆周轮廓,如图6所示。图5和图6中的轮廓未按比例绘制,由程序生成,局部放大比为2 000。

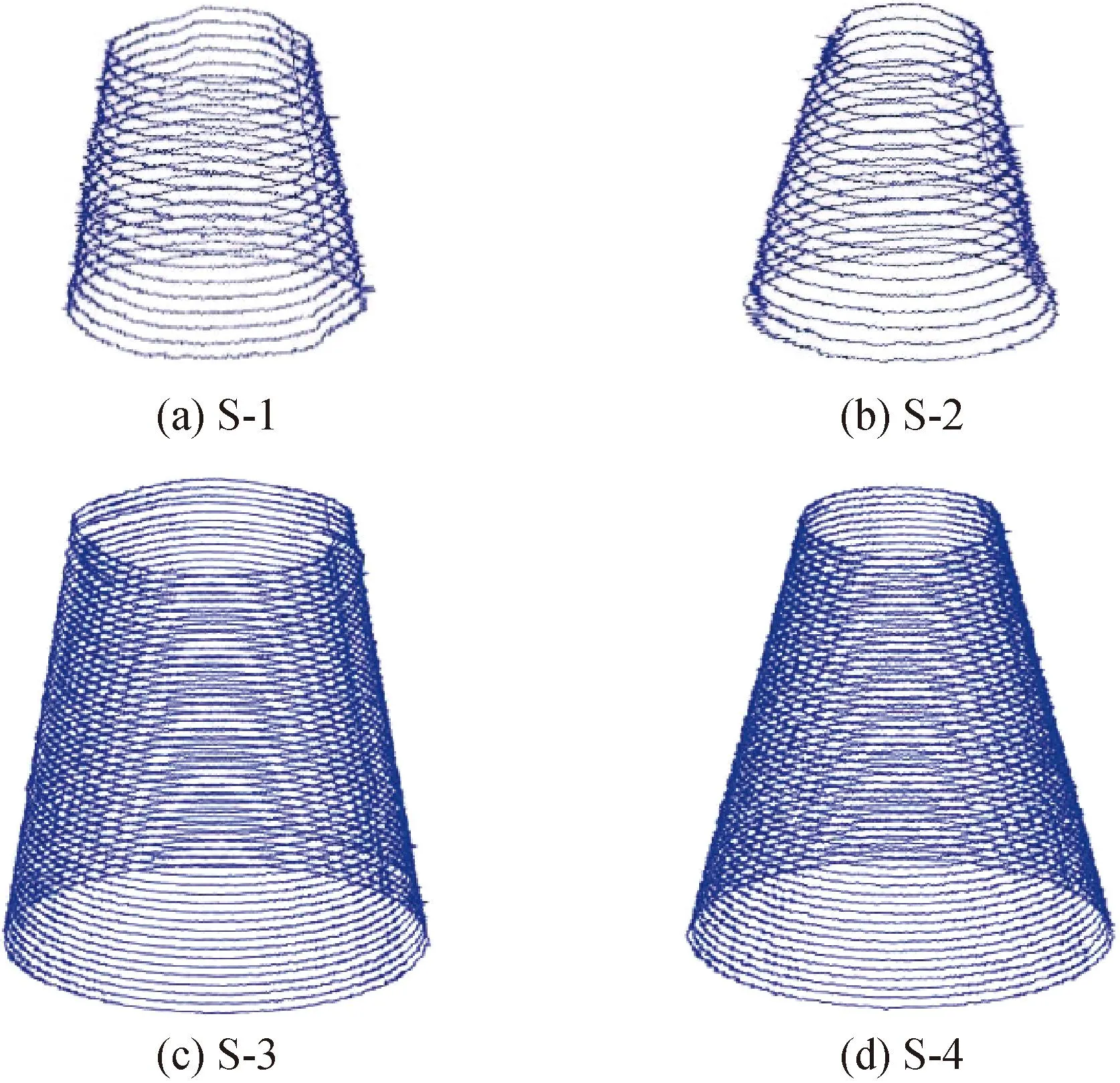
图6 4个圆锥仿真试样圆周轮廓示意图Fig.6 Schematic of roundness profiles of four cone simulated samples

基于式(1)和式(4),对4个圆锥仿真试样的最小二乘全局角度尺寸进行了评定,最小二乘全局角度尺寸αL和最小二乘圆锥相关参数xL1,yL1,pL,qL,RL1和TL见表2～表5。基于式(1)、式(2)和图4,用非线性最小二乘法对4个圆锥最小二乘全局角度尺寸进行了评定,最小二乘全局角度尺寸αLn和最小二乘圆锥相关参数xLn1,yLn1,pLn,qLn,RLn1和TLn见表2～表5。

表2 圆锥试样S-1的最小二乘全局角度尺寸评定结果Tab.2 Evaluation results of least square global angular sizes of cone sample S-1

表3 圆锥试样S-2的最小二乘全局角度尺寸评定结果Tab.3 Evaluation results of least square global angular sizes of cone sample S-2

表4 圆锥试样S-3的最小二乘全局角度尺寸评定结果Tab.4 Evaluation results of least square global angular sizes of cone sample S-3

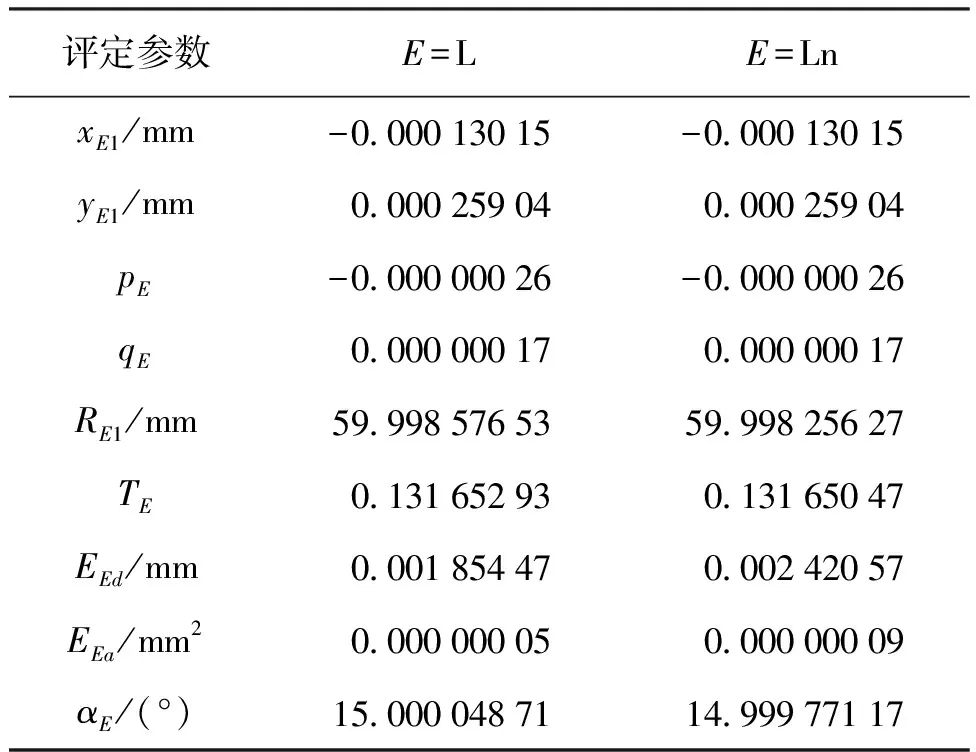
表5 圆锥试样S-4的最小二乘全局角度尺寸评定结果Tab.5 Evaluation results of least square global angular sizes of cone sample S-4

用非线性最小二乘法评定最小二乘全局角度尺寸时,将CLs=[xLs1yLs1pLsqLsRLs1TLs]作为搜索CLn的优化初始参数CLn0,由式(9)确定。

(9)

用最小二乘圆锥参数CL=[xL1yL1pLqLRL1TL]或CLn=[xLn1yLn1pLnqLnRLn1TLn]作为MFO评定圆锥最大最小全局角度尺寸优化时的初始参数CM0。

对于圆锥角度尺寸优化时的初始参数CE0k,k=1,…,6。全局角度尺寸优化参数CE的下、上搜索边界可由式(10)确定。

(10)

式中:bc和c均为搜索边界系数,本文中bc和c分别为40和0.3;f可由式(11)确定。

(11)

式中1≤j≤n。

表2～表5中,EEa为最小二乘方法的优化特征值,可由式(12)确定,即,

(12)

由表2～表5可知:线性最小二乘方法和非线性最小二乘方法评定全局角度尺寸得到的圆锥轴线参数基本相同;对于试样S-1、S-2、S-3,2种最小二乘方法评定得到特征值ELa与ELna相同、全局角度尺寸αL与αLn基本相同;对于试样S-4,尽管2种最小二乘方法得到的参考圆锥的轴线参数相同,但由于两种方法的RL1和RLn1不同、TL和TLn不同,导致优化特征值EEa与ELna不相同,两种最小二乘方法得到的全局角度尺寸之差为0.997″。总体上讲,线性最小二乘方法在评定精度和效率方面优于非线性最小二乘方法。

表6～表9为基于式(5)和图4,优化参数初始值CM0分别等于CL和CLn,由MFO优化得到的圆锥最大最小全局角度尺寸及其相关参数的评定结果。表中,EMd为最大最小全局角度尺寸评定效果的优化特征值,EMd值小者,其对应的圆锥最大最小全局角度尺寸的评定精度高。EMd可表示为:

表6 圆锥试样S-1的最大最小全局角度尺寸评定结果Tab.6 Evaluation results of minimax global angular sizes of cone sample S-1

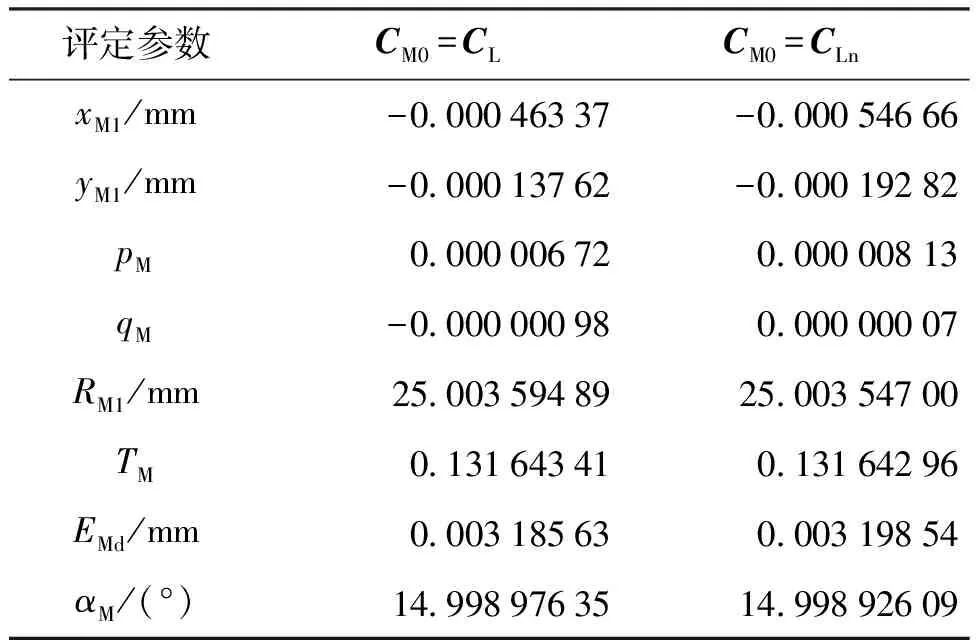
表7 圆锥试样S-2的最大最小全局角度尺寸评定结果Tab.7 Evaluation results of minimax global angular sizes of cone sample S-2

表8 圆锥试样S-3的最大最小全局角度尺寸评定结果Tab.8 Evaluation results of minimax global angular sizes of cone sample S-3

表9 圆锥试样S-4的最大最小全局角度尺寸评定结果Tab.9 Evaluation results of minimax global angular sizes of cone sample S-4

EMd=maxdMij-mindMij

(13)

式中:1≤i≤m; 1≤j≤n;dMij的含义见式(6)。将式中的下标M换成L或Ln,即可确定表2～表5中的EEd。

由表6～表9可以看出:优化参数初始值影响最大最小全局角度尺寸的评定精度。对于试样S-1和S-2,优化参数初始值CM0等于CL时的EMd小于优化参数初始值CM0等于CLn时的EMd,说明前者最大最小全局角度尺寸αM的评定精度高于后者的评定精度;对于试样S-3和S-4,情况与试样S-1和S-2相反,优化参数初始值CM0等于CLn时得到的最大最小全局角度尺寸αM的评定精度高于CM0等于CL时的评定精度。MFO是1个全局优化算法,从理论上讲,不同优化初始参数得到的优化特征值EMd应基本相同,但两者实际上还是有差别的。表6～表9中试样S-1、S-2、S-3和S-4对应于2个优化初始值的EMd之差(单位:mm)分别为-1.71×10-6、-1.29×10-5、9.1×10-7和1.26e×10-6,对应的最大最小全局角度尺寸αM值之差分别为-0.046″、0.181″、0.068″和-0.012″。

为了使最小二乘圆锥面和最大最小圆锥面评定结果可视化,将上述确定最小二乘圆锥面和最大最小圆锥面相关参数的计算方法用于图6所示的局部放大轮廓的最小二乘圆锥面和最大最小圆锥面的相关参数的计算。以最小二乘全局角度尺寸评定的可视化为例,4个圆锥面仿真试样轮廓及其最小二乘参考圆锥面的可视化如图7所示。

图7 四个圆锥仿真试样的最小二乘圆锥面可视化Fig.7 Visualization of least square cones of four cone simulated samples

4.2 讨论

由表2～表9中的EEd和EMd值可知,4个圆锥试样的EMd值均小于EEd值,与最大最小评定准则一致。

由表2～表5中的优化特征值EEa和表6～表9中的优化特征值EMd可以看出,评定结果可能未达到最优。实际上,影响MFO算法优化结果的因素很多,如边界系数bc和c、优化初始值、种群大小N和最大迭代次数T等。表2～表9中的值评定时,N和T分别为20和500。

本文以圆锥试样S-4的最大最小全局角度尺寸为例说明边界系数bc和c以及N和T对评定结果的影响,将上述参数进行了5组组合对优化特征值和圆锥最大最小全局角度尺寸进行评定。优化参数分组如下:组Ⅰ:bc、c、N和T分别为40、0.3、10和500;组Ⅱ:bc、c、N和T分别为40、0.3、30和500;组Ⅲ:bc、c、N和T分别为40、0.3、20和200;组Ⅳ:bc、c、N和T分别为1、0.2、20和500;组Ⅴ:bc、c、N和T分别为40、0.3、20和500。

5组优化特征值EMd和最大最小全局角度尺寸αM评定结果如图8所示。

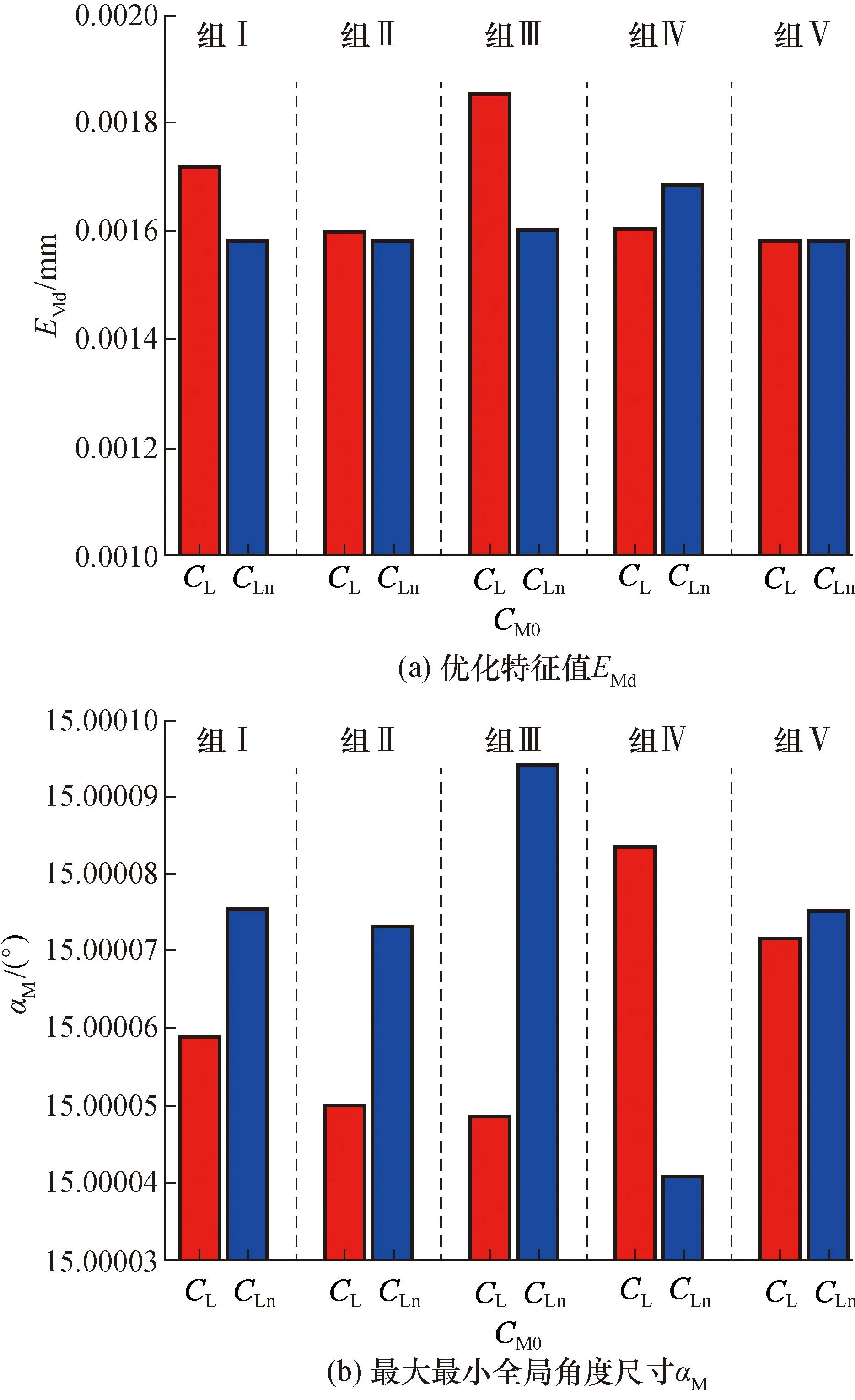
图8 圆锥试样S-4不同优化参数组合下的EMd和αM评定结果Fig.8 Evaluation results of EMd and αM of cone sample S-4 under different combinations of optimization parameters

由图8(a)可以看出,表5和表9选用的优化参数组合(组Ⅴ)在5组组合中是较佳的组合,其优化特征值相对较小。由图8(b)可以看出,当CM0=CL时,5种组合的最大最小角度尺寸αM的最大值与最小值之差为0.125″,当CM0=CLn时,5种组合的最大最小角度尺寸αM的最大值与最小值之差为0.191″。由图8可以看出,CL和CLn分别选作CM0时,组Ⅲ的αM2个评定结果相差较大,其差为-0.164″,组Ⅴ的相差较小,其差为-0.012″。由上述分析可知,优化参数的组合和CM0的选用,对评定结果均有一定的影响,但规律性不强。为使全局角度尺寸评定达到较高的精度,需要通过大量的实验和评定,探索较佳的优化参数组合。

为进一步验证MFO在圆锥全局角度尺寸评定中的适应性,选择组Ⅴ的优化参数组合,用CSA、AEO、EO、粒子群算法(particle swarm optimization,PSO)4种算法对4个试样的最大最小全局角度αM进行评定,获得相应的优化特征值EMd,见图9,图中,CSA、AEO、EO和PSO的8个优化特征值EM小于MFO对应的优化特征值EMd的个数分别为1、3、2和1。总体上讲,MFO的评定结果优于其他4种优化方法的评定结果。尽管基于MFO的评定结果并非全局最优,但其评定精度可以满足圆锥全局角度尺寸评定的需要。

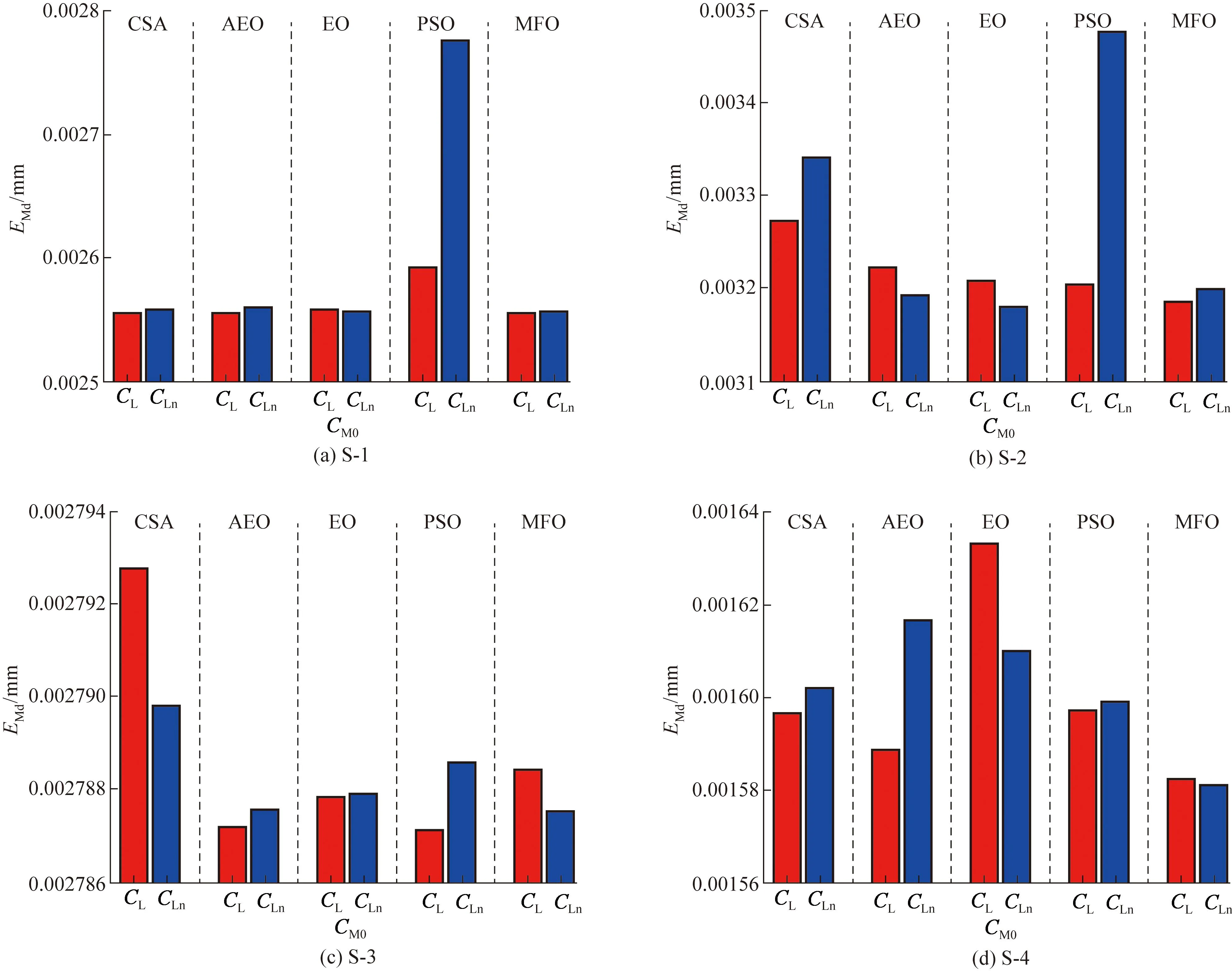
图9 四个圆锥试样不同优化优化算法的EMd评定结果Fig.9 Evaluation results of EMd of four cone samples under different optimization algorithms

除了用EMd值评价优化算法的圆锥全局角度尺寸的评定精度外,优化算法的评定效率也是评价其在圆锥全局角度尺寸评定中的适应性的一个重要方面,5种优化算法的评定效率如表10所示。表中,ΓLn和ΓM分别表示非线性最小二乘全局角度尺寸和最大最小全局角度尺寸每1 000采样点的评定时间(单位:s),ΓLn和ΓM由式(14)计算得到。

表10 5种优化算法的评定效率Tab.10 Evaluation efficiencies of five optimization algorithms

E=Ln,M

(14)

式中:圆锥试样S-1、S-2、S-3和S-4的全局角度尺寸评定时间分别为tE1、tE2、tE3和tE4;圆周轮廓数分别为m1、m2、m3和m4;每个圆周轮廓的采样点数为n1、n2、n3和n4。

由表10可以看出,5种优化算法中,MFO的评定效率略低于CSA和PSO的评定效率,但高于AEO和EO的评定效率。综合考虑评定精度和评定效率,MFO尽管尚未实现全局最优,但可以满足圆锥全局角度尺寸评定的需要。

5 结 论

根据圆锥全局角度尺寸的定义,提出了基于圆周轮廓提取方案的最小二乘全局角度尺寸和最大最小全局角度尺寸评定方法,建立了圆锥最小二乘全局角度尺寸评定模型和最大最小全局角度尺寸评定模型。基于圆锥全局角度尺寸评定模型,给出了MFO评定圆锥全局角度尺寸的流程图,并编制了相应的圆锥全局角度尺寸评定程序。采用所编制的评定程序,对4个圆锥仿真试样进行了全局角度尺寸评定,并给出了相应的评定结果。

将线性最小二乘圆锥面参数CL和非线性最小二乘圆锥面参数CLn分别作为最大最小圆锥面优化的初始参数,4个圆锥试样的基于MFO的对应试样2个最大最小圆锥面优化特征值EMd之差位于-1.291×10-5～9.1×10-7mm之间,2个最大最小全局角度尺寸αM之差位于-0.046″～0.181″之间。评定结果表明:MFO的圆锥全局角度尺寸评定尚未实现全局最优;且优化初始值、搜索区间、种群数、最大迭代数等对评定结果均有一定的影响,但其缺乏规律性。总体上讲,MFO评定结果优于CSA、AEO、EO和PSO四种优化算法的评定结果。