抚河流域极端降水变化及其对输沙量的影响

肖 谷

(德兴市审计技术保障中心,江西 上饶 333299)

随着气候变化,极端降水事件不断增加,严重影响着人们的生产生活。极端降水事件造成严重的流域水土流失,其对流域土壤的侵蚀随着水文过程形成河流输沙[1]。因此,了解极端降水事件与输沙量之间的关系可以直接掌握流域土壤流失情况。

目前,钟科元等[2]研究了松花江流域极端降水和输沙量之间的关系,结果表明,极端降水指标与输沙量具有显著相关性,其中降水强度指数(SDII)对输沙量的影响最大;周才钰等[3]分析了黄河中游极端降水对输沙量的影响,发现2000年以后极端降水对输沙量的影响要小于人类活动的影响;孙维婷[4]研究发现延河流域极端降水与输沙量在1970—1996年呈显著线性相关,但1996—2010年间的线性相关关系减弱;任玉玲[5]评估了黄土高原极端降水对水沙的影响,表明人类活动是流域水沙量减小的主要原因。以上研究通过分析极端降水指数与输沙量之间的关系,为流域水土保持工作提供了科学依据。

鄱阳湖流域,极端降水强度大、频率高,时常引发洪涝灾害和土壤侵蚀事件[6]。因此,研究者开展了该地区极端降水时空演变特征分析。王怀清等[7]研究发现鄱阳湖流域极端降水事件概率增大,洪涝灾害风险增加;高冰等[8]研究发现抚河流域极端降水事件增加趋势显著,而极端降水天数却呈减少变化。此外,顾朝军等[9]研究了鄱阳湖流域降水侵蚀力和输沙量之间的关系,发现近60年来降水侵蚀力变化使得流域输沙量增加;曾瑜等[10]研究表明年降水和降水侵蚀力是影响鄱阳湖输沙量的关键指标。为进一步研究分析鄱阳湖流域极端降水事件及其对输沙量的影响,本文以鄱阳湖抚河流域为例,选用抚河流域1960—2018年控制性水文站逐日输沙量和气象站逐日降水资料,统计了8种极端降水指标,以此探究抚河流域极端降水的时空变化特征及其对输沙量的影响程度,以期为抚河流域水土保持生态建设提供帮助。

1 资料与方法

1.1 研究区概况与数据

抚河流域位于江西省东部,是鄱阳湖五大子流域之一,位于东经115°36′～117°10′,北纬26°30′～28°20′,见图1。东接福建,南临赣江,西毗沂江、乌江,从北流入鄱阳湖,流域总面积约为1.56万km2,抚河发源于武夷山区,干流长约350km,自南向北贯穿整个流域。流域三面环山,北部为湖区平原,以丘陵、山地为主,丘陵占53.1%,山地占29.5%;岗地、平原次之,其中岗地占10.3%,平原占7.1%。流域属亚热带季风气候,雨量充沛,但年内分布不均,降水主要发生在4—6月,并且极端降水事件不断增加,使得该流域成为鄱阳湖流域土壤侵蚀量增幅明显的地区之一[11]。

图1 抚河流域概况

本文收集了抚河流域10个国家气象站1960—2018年逐日降水量资料,该数据来源于江西省气象信息中心;收集了抚河流域控制性水文站——李家渡水文站1960—2018年逐日输沙量资料,该数据来源于江西省水文监测中心。数据真实可靠。

1.2 研究方法

1.2.1 极端降水指数

本文选用了气候变化监测与极端气候事件指数专家组(ETCCDI)表征极端降水事件的降水强度(SDII)、最大5日降水量(RX5d)、最大1日降水量(RX1d)、大于95%分位数强度降水量(R95P)指数,使用极端气候指数计算软件(RClimdex)统计该4种计算降水指数。另外,暴雨量(RSP)、大雨量(HP)、汛期降雨量(FSPTOT)和侵蚀性降水量(ERPTOT)4种指数也被学者认为是影响土壤侵蚀的重要指数[12,13]。

1.2.2 Mann-Kendall趋势分析

本文采用Mann-Kendall(M-K)趋势分析评估抚河流域8种极端降水指数和输沙量年际变化趋势。该方法计算不受样本、分布类型的影响,是一种广泛应用在水文气象领域的非参数统计检验方法。对于1960—2018年共59年时间长度的极端降水和输沙量序列(X1,X2,…,X59),若M-K检验统计值Z>0,表明序列呈增加趋势;若Z<0,表示序列呈减小趋势;当Z>1.96时,表明序列趋势变化显著;当Z>2.32时,表明序列趋势极显著。

1.2.3 双累积曲线

本文中采用广泛应用于水文要素驱动力分析的双累积曲线方法,该方法能够辨别水文要素的长期变化趋势和气候变化与人类活动对其影响的贡献程度[14]。该方法基于对水文要素时间序列的突变分析,划分水沙变化的基准期与变化期。首先,在基准期极端降雨主导河流输沙量的变化,人类活动影响较小,因此构建近自然条件下极端降水量-输沙量之间的双累积线性函数关系。其次,在变化期通常人类活动对降水输沙量关系产生较大影响,将变化期年份的降水数据带入基准期的线性函数关系中,获得变化期近自然条件下输沙量理论值,此时变化期输沙量实测值与理论值之间的差值为人类活动影响量,而变化期理论值与基准期之间的差值为极端降水指数的影响量,变化期与基准期实测输沙量的差为输沙量变化量。最后,计算人类活动与极端降水指数对输沙量的贡献率,人类活动的贡献率为人类活动影响量与输沙量变化量的比值,极端降水指数的贡献率为极端降水指数的影响量与输沙量变化量的比值。

1.2.4 交叉小波分析

(1)

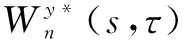
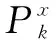
(2)

式中:σx、σy分别为输沙量与极端降水指数序列的标准差;Zv(p)为概率p对应的置信度;v为自由度。

2 结果分析

2.1 极端降水时空特征

2.1.1 年际变化特征

图2为抚河流域1960—2018年8种极端降水指数的年际变化过程,研究期内抚河流域极端降水指数均呈不同程度的增加趋势,其中,SDII呈极显著增加趋势(Z=2.82,P<0.01),R95P和HP具有较强的增加趋势,RX1d和RX5d增加趋势较弱;各极端降水指数变化过程相近,在1960—1987年波动变化,1987—1997年出现明显增加趋势,之后开始减小,从2008年开始再次增加;在研究期内极端降水指数大致呈现出两个完整的波动周期,第一个波动周期为19世纪60年代至80年代末,第二个周期为1990年初至2000年末;各极端降水指数除FSPTOT外,其他极端降水指数均在1998年出现明显的极值点,表明抚河流域1998年发生了明显的极端降水事件。

图2 极端降水指数年际变化过程

2.1.2 空间变化特征

图3为抚河流域1960—2018年多年平均极端降水指数空间分布情况,抚河流域主要呈现三种不同的空间分布格局,RX1d、SDII、RSP空间分布大致呈现北高南低分布,由北向南极端降水逐步减小;R95P、RX5d、FSPTOT、ERPTOT空间分布大致呈东高西低;而HP空间分布大致为南高北低。极端降水指数低值主要分布在宜黄县附近,高值指数主要在东乡和南城地区。

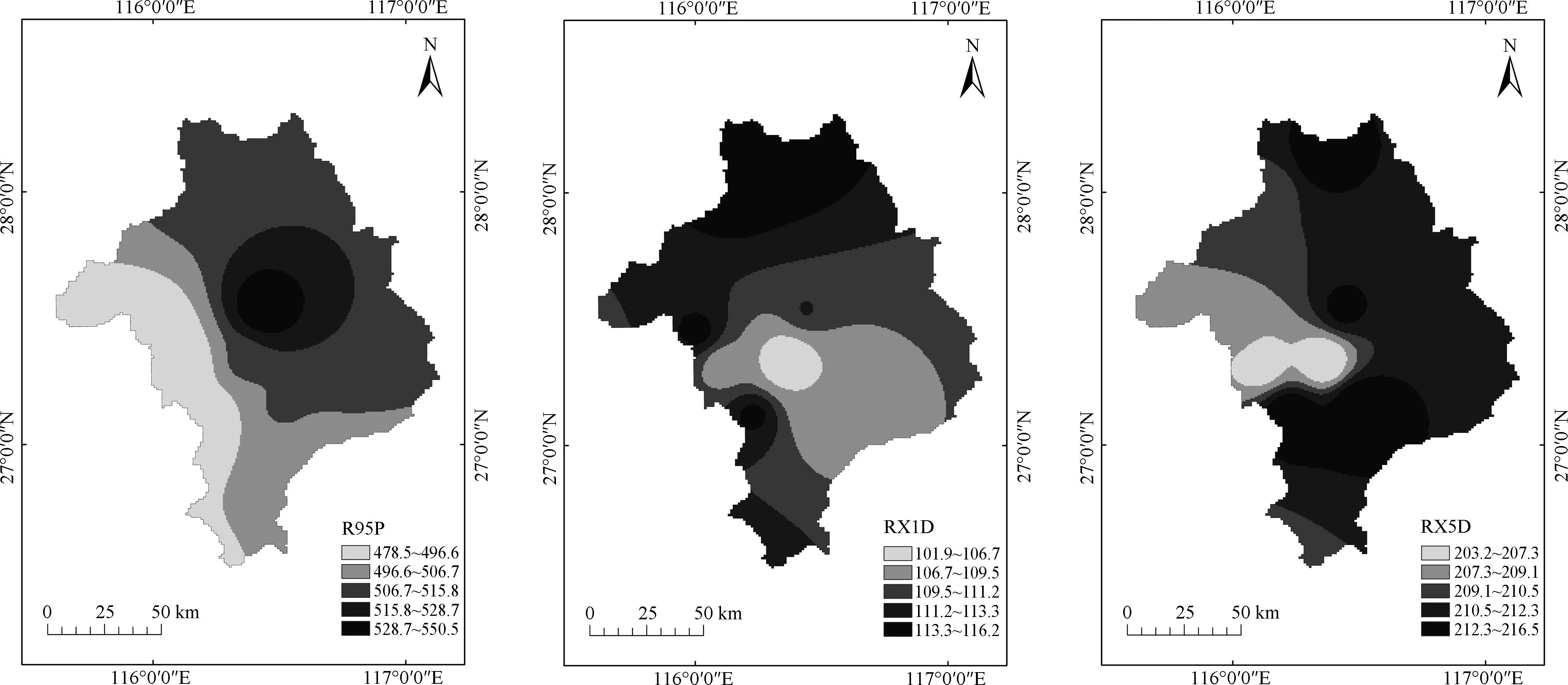
图3 极端降水指数空间分布

2.2 极端降水对输沙量的影响

2.2.1 输沙量的年际变化

1960—2018年,抚河流域输沙量总体上呈现减少趋势,见图4,M-K趋势统计分析检验值Z=-1.48,呈不显著的减小趋势;年最大输沙量发生在1998年,最小输沙量发生在1963年;年输沙量总体上呈现3次上升过程,第一次为1985年以前,年输沙量波动性上升,第二次为1991—1998年;第三次为2007—2016年。详见图4。

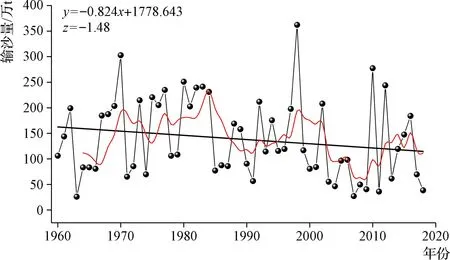
图4 输沙量变化

2.2.2 极端降水与输沙量的双累积曲线分析

利用极端降水指数与输沙量之间的双累积曲线判断它们关系变化,由图5可知,极端降水指数与输沙量的双累积曲线关系在1997年发生转变,1998—2018年双累积曲线斜率均小于1960—1997年,表明1998年以后,流域输沙量出现了明显的减小变化。因此,以1997作为变化点,将1960—1997年作为基准期,1998—2018年作为变化期。

图5 极端降水指数和输沙量双累积曲线

2.2.3 极端降雨对输沙量的贡献率

相比于基准期,抚河流域变化期年输沙量减少34.576万t,减小幅度达22.9%。表1给出了变化期极端降水指数对输沙量减小的贡献率,极端降水指数均对输沙量产生促进作用,其中,RSP和R95P的增沙作用明显强于其他极端降水指数;FSPTOT对输沙量的增加贡献最小,为33.07%。虽然流域极端降水指数均呈不同程度的增加变化趋势,但图4中输沙量呈减少变化趋势,这也表明了人类活动在输沙量的减少过程中起到主导作用。

表1 抚河流域极端降水指数对输沙量的贡献率

2.3 交叉小波分析

为探究极端降水变化对输沙量的影响程度,使用交叉小波变换分析抚河流域八种极端降水指数和输沙量的关系。极端降水指数与输沙量之间的交叉小波谱图(见图6)中,细弧线内为小波影响椎内的有效谱值,实线内为红噪声标准谱(通过95%显著性检验)。图谱箭头向右,表明八种极端降水均与输沙量同相位,极端降水指数均与输沙量呈正相关。除RX1d和HP外,其他极端降水指数与输沙量在1986—1998年存在约16年时间尺度上的显著共振关系;在7年左右时间尺度上,RX1d在1968—1982年和RX5d在1968—1986年共振关系显著;在4年左右的时间尺度上,极端降水指数与输沙量呈正相关,平均相位角约-45°,表明极端降水指数超前输沙量0.5年。同时,在1年短周期时间尺度上,极端降水指数与输沙量存在显著共振关系,但通过显著性检验的区域较小。

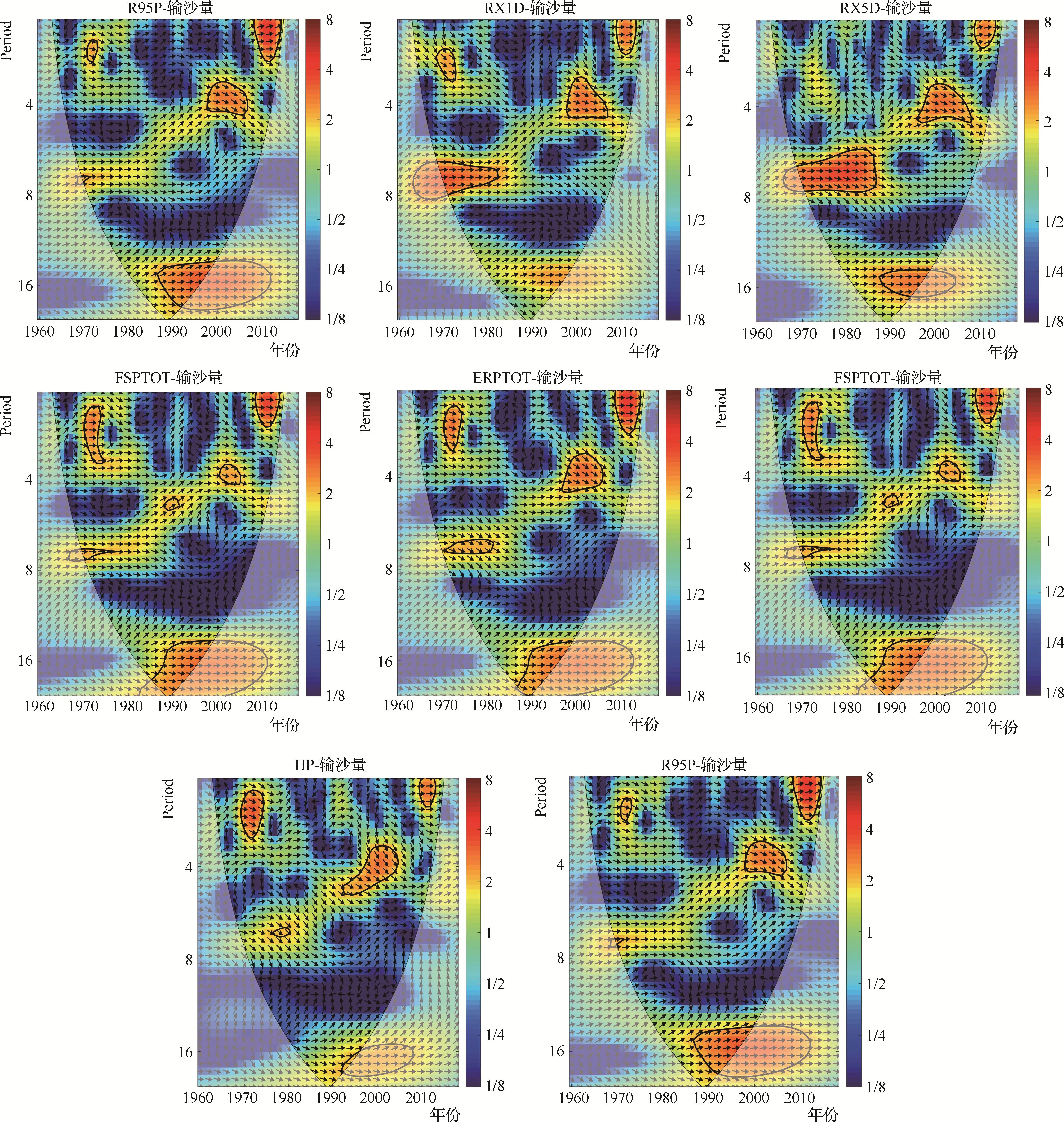
图6 极端降水指数与输沙量交叉小波图

3 结 论

探究极端降水变化规律及其对输沙量的影响对流域水土保持生态建设具有重要意义。基于抚河流域近60年逐日降水量和输沙量资料,分析八种极端降水指数的时空变化及其对输沙量的影响。研究结论如下:

a.抚河流域八种极端降水指数均呈不同程度的增加趋势,SDII呈极显著增加趋势(P<0.01),其次为R95P和HP,具有较强的增加趋势,RX1d和RX5d增加趋势不明显。

b.RX1d、SDII、RSP指数空间上大致呈现“北高南低”的分布,RX5d、FSPTOT、ERPTOT指数空间上分布为“东高西低”,而HP指数空间分布则为“南高北低”。

c.抚河输沙量呈不显著的减小趋势(z=-1.48),人类活动是流域输沙量减小的主导因素,极端降水指数均对输沙量产生促进作用,其中RSP和R95P的增沙作用明显强于其他极端降水指数,FSPTOT对输沙量的增加贡献最小。

d.极端降水指数和输沙量呈正相关,总体上存在1年、4年、16年的周期性显著共振关系,其中在4年时间尺度左右,极端降水指数超前输沙量0.5年。