基于服务质量的虚拟化云资源动态分配算法∗

李凯锋 胡 泓 吴海燕 贺莉娜 胡 宇

（1.南瑞集团公司（国网电力科学研究院） 南京 211000）（2.国电南瑞科技股份有限公司 南京 211106）（3.北京市轨道交通运营管理有限公司 北京 100068）

1 引言

随着互联网和信息化技术的不断进步，越来越多的应用由于其数据量指数级的增长，必须通过借助云资源来实现，云计算［1］的时代已经来临。云服务提供者通过将数据中心的多种基础资源进行深度整合，实现对计算资源、网络资源、存储资源的虚拟化和统一化调度管理［2］，并通过调度中心为用户申请的任务分配资源。

然而，云计算的动态特性决定了云资源分配时，既要满足不同任务服务质量［3］（quality of service，QoS）的需求，还要增加云平台的吞吐量，提高资源利用率。经典的遗传算法［4～7］、模拟退火算法［8～10］、蚁群算法［11～14］和粒子群算法［15～16］等云资源分配算法，主要将注意力集中在如何缩短任务的完成时间，而不注重任务的服务质量需求（包括时间、成本、安全性和可靠性等），这会导致用户的满意度降低。蚁群算法虽然可实现群体性的组合优化，但由于初期信息素的平均分配，存在过多的盲目搜索行为，影响算法效率。

针对以上不足，本文提出了一种基于服务质量的云资源动态分配算法，根据用户的时间、成本、安全性和可靠性四种服务质量需求建立数学模型，对云资源动态分配算法进行约束。将遗传算法与蚁群算法相结合，利用遗传算法更新信息素矩阵后，再使用动态融合策略获得两种算法的最优融合时间，最后通过蚁群算法求出最优解，优化了虚拟资源负载，提高了用户满意度。

2 服务质量数学模型

虚拟化的云资源动态分配就是云服务提供者将计算资源按照用户的需求分配给用户的过程。进行虚拟云资源分配需要在符合用户服务质量需求的前提下，将独立的任务分配给有效的虚拟资源，让虚拟资源被高效合理地利用。本文将用户对服务质量的需求分为时间需求、成本需求、可靠性需求和安全性需求四个方面，并建立了服务质量数学模型。

设任务集合T={t1,t2,…,tn}，表示当前有n个等待处理的任务在任务队列中。云资源集合R={r1,r2,…,rm}，表示当前有m个有效资源在资源池内，其中资源是云计算中处理任务的基础运算单位。

时间归属函数TM(i,j)如式（1）所示：

式（1）中，RTij表示任务ti在资源rj中执行的预期执行时间，RT(i,j)表示任务ti在资源rj中执行的实际执行时间。

成本归属函数CM(i,j)如式（2）所示：

式（2）中，Cij表示任务ti在资源rj中生成的预期成本，C(i,j)表示任务ti在资源rj中生成的实际成本。

安全性归属函数SM(i,j)如式（3）所示：

式（3）中，TSij表示任务ti对资源rj的期望安全级别，Sij表示资源rj提供给任务ti的实际安全级别，Smax表示任务的最高安全级别。

可靠性归属函数RM(i,j)如式（4）所示：

式（4）中，TRij表示任务ti对资源rj的期望可靠性，SRij表示该资源rj提供给任务ti的实际可靠性。

服务质量目标函数如式（5）所示：

在（5）中，λ1、λ2、λ3、λ4分别表示服务质量目标函数中的时间，成本，安全性和可靠性权重。

3 服务质量约束的遗传-蚁群资源分配算法

3.1 服务质量约束的遗传-蚁群算法基本思想

由于遗传算法的后期运算效率较低，易导致许多的重复迭代。而蚁群算法每条路径在初始时期的信息素都相同，盲目性较高，浪费了大量搜索时间。因此本文考虑了用户对服务质量的多种需求指标，将遗传算法与蚁群算法相结合，提出了服务质量约束的遗传-蚁群资源分配算法。此算法分为如下三部分：

1）利用遗传算法的全局快速搜索能力，并将所获得的全局搜索信息转化成蚁群算法的初始信息素。

2）判断遗传算法和蚁群算法融合的正确时间。

3）利用蚁群算法的正反馈和高效收敛的特性，完成满足服务质量条件的云资源最优分配。

3.2 遗传算子全局快速搜索

3.2.1 染色体编码

本文将染色体的长度定义为任务的数量，并通过编码处理任务。染色体内的基因值是与其位置相应任务所利用的资源数量。定义云环境中的初始系统规模是S，任务集内n个任务被随机分发给m个空闲的资源，n表示染色体的长度，1 与m范围内的随机数则表示单个基因的值。

3.2.2 适应度函数

适应度主要用来评估群体中个体的质量，本文选择服务质量目标函数的倒数作为适应度函数。服务质量目标函数的四个指标系数满足λ1+λ2+λ3+λ4=1，可根据用户需要设置相应的权重。

3.2.3 选择、交叉和变异操作

选择操作使用轮盘赌方式生成选择算子，选择概率通过任务调度适应度值占所有任务适应度值的比值进行计算。

使用戴维斯顺序交叉法进行交叉操作，设常数Pc为交叉概率。变异操作则利用逆向变异法，设常数Pm为变异概率。

3.3 遗传算法与蚁群算法的融合

遗传算法和蚁群算法的融合非常困难，一般方法是把遗传算法设成固定迭代运行，但是运算结束的太早或太晚都会影响算法的效率。因此本文使用动态的结合方式来保证蚁群算法和遗传算法在最优的时间点进行结合。

1）设置最小遗传迭代次数Genemin和最大遗传迭代次数Genemax。

2）计算子代群体在遗传迭代过程中的进化速率，并设置子代种群的最小进化速率为Genemin-impro-ratio。

3）如果后代种群的连续迭代Genedie(Genemin≤Genedie≤Genemax) 的 进 化 速 率 小 于Genemin-impro-ratio，则可以证明遗传算法优化速度较低，那么系统就可终止遗传算法流程并进入蚁群算法流程。

3.4 蚁群算子精确求解

3.4.1 初始化信息素

3.4.2 选择操作

在t时刻，可以将资源j分配给任务i的概率表示为

在式（9）中，τj表示t时刻资源j上信息素的浓度。ηj表示资源的可见性，即启发式信息。η=aP+bB，P表示CPU 的处理能力，B表示网络带宽，a和b分别表示处理能力和带宽在资源可见性中的比例系数。α是信息素因子，体现运动轨迹的重要性；β是启发式因子，体现期望值的重要性。

3.4.3 信息素更新

局部信息素更新：当蚂蚁完成所有任务的资源分配时，将更新所有分配资源的信息素残留量。假设τj(t)是t时刻上资源rj的信息素，那么在t+1 时刻，资源rj的信息素更新规则如下：

在式（10）中，1-ρ为信息素残留因子，ρ表示信息素挥发因子(0<ρ<1)。∆τ(t)可以从式（11）得到，其中L表示资源数量。

全局信息素更新：当全部的蚂蚁都结束一次迭代时，根据式（5），可以在该次迭代中求解出全局最佳调度方案，并全局更新最佳调度方案中资源的信息素。

基于服务质量的遗传-蚁群云资源分配算法流程如图1所示。

图1 遗传-蚁群云资源分配算法流程图

4 仿真实验与分析

4.1 实验仿真

为了测试本文设计的算法性能，选择Cloudsim5.0.3 云仿真平台对蚁群算法、遗传算法、遗传-蚁群算法进行了仿真和结果对比分析。在云仿真平台Cloudsim5.0.3中配置云环境的初始条件，包括创建数据中心、初始化任务规模参数、配置输入输出数据文件大小及任务大小和创建虚拟机资源，包括CPU、带宽和内存等。在DatacenterBroker 类中构造遗传-蚁群算法、遗传算法和蚁群算法三种算法。

设置服务质量目标函数权重：λ1=0.2 ，λ2=0.3，λ3=0.22，λ4=0.28。设置选择参数的概率：α=0.7，β=0.3，ρ=0.4。表1 所示为遗传蚁群算法相关仿真参数。

表1 遗传-蚁群算法相关仿真参数

4.2 结果分析

本文的算法将用户服务质量作为资源分配的约束函数，结合蚁群算法和遗传算法的双重优势，提高了求解的收敛速度。比较分析了遗传算法、蚁群算法和服务质量约束的遗传-蚁群算法，并实现了仿真示例。资源负载计算公式如下所示。

式（14）中，Loadj是资源j 的负载，Loadavg是负载的平均值。仿真结果分别如图2和图3所示。

图2 资源负载对比图

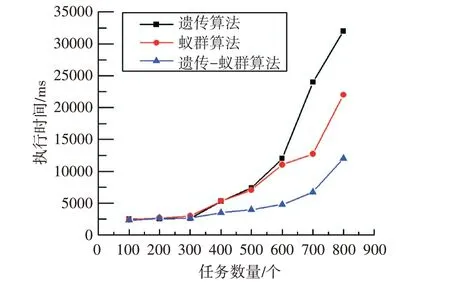
图3 执行时间比较

分析图2 结果可发现，随着任务数量的增加，三种算法资源的负载率也随之增加。但是与遗传算法和蚁群算法相比，基于服务质量的遗传-蚁群算法的资源负载率变化较小，并且始终保持较低的水平。与遗传算法和蚁群算法相比，基于服务质量的遗传-蚁群算法的资源负载率分别提高了28%和24.1%。因此，基于服务质量的遗传-蚁群算法的虚拟资源分配结果更加趋于高效合理，云平台的负载均衡度也在不断提高。

根据图3 可发现，三种算法的任务数量与执行时间之间都存在正相关的关系。当任务数量大于500 时，随着任务数量的增加，三种算法的执行时间都有所增加，可见任务数量的增加会影响算法执行的效率。蚁群算法和遗传算法的执行时间都远多于服务质量约束的遗传-蚁群算法的执行时间，并且执行时间保持在较低水平。因此，不论是运算的时间效率还是寻找最佳解的效率，基于服务质量的遗传-蚁群算法均超过单个的遗传算法与蚁群算法。

5 结语

本文提出了一种基于服务质量的虚拟云资源动态分配算法，该算法考虑了多种服务质量指标，通过将遗传算法和蚁群算法融合并将服务质量指标转换为归属函数作为遗传算法的适应度函数，求得的最优解能够满足用户的服务质量需求。在CloudSim云计算平台进行的仿真结果表明，该算法在资源负载均衡角度和时间花费角度都好于单个遗传算法与蚁群算法，在最大化云计算资源利用效率的同时，明显提升了服务质量。