基于J2 摄动项的Runge-Kutta、Hermite 数值轨道预报方法∗
张政超 朱 峰 郭伟锋 周 磊
(63891部队 洛阳 471000)
1 引言
近年来,对卫星轨道的研究方法层出不穷[1~5],对卫星轨道的描述方法和卫星轨道的预测更是持续不断的研究热点[6~8]。一方面随着人们对开普勒三定律的深入认识,对卫星轨道的描述使用惯性坐标系下的模型普遍被接受,另一方面,由于星上计算资源的有限,利用当前的位置、速度信息准确、快速、高效地预测卫星此后一段时间的轨道信息,为星上任务设备的姿态控制提供参考依据便变得十分有意义和重要。
虽然星上任务设备对卫星的轨道信息的精度要求不是很高,但在无GNSS信息,仅靠上注信息的情况下,随着时间的增长,卫星轨道的精度很快就会下降,甚至断崖式下跌[9~12],解决的办法是选用合适的轨道预测方法、定时上注、多源信息融合等。本文仅对预测方法进行分析和仿真,解决了一定精度下对卫星轨道的预报问题,其他不多赘述。
2 卫星轨道的表示方法及坐标转换
2.1 表示方法
对卫星轨道信息的描述主要分时间系统和坐标系统。
时间系统包括UTC 时间和北京时间。坐标系统包括WGS84坐标系下的笛卡尔坐标(3维位置、3维速度)、J2000.0 坐标系下的轨道六根数(长半轴、偏心率、倾角、升交点赤经、近地点幅角、真近点角)或笛卡尔坐标(3 维位置、3 维速度)。一般来说,测控时选用的WGS84 坐标系下的笛卡尔坐标,研究轨道性质选用的是J2000.0坐标系下的轨道六根数或笛卡尔坐标,三者之间可以互换。
2.2 WGS84坐标系转换到J2000.0坐标系
J2000.0坐标系与WGS84坐标系主要在方面不同,WGS84 坐标系(协议地球坐标系)转换到J2000.0 坐标系(协议天球坐标系)需进行极移、格林尼治恒星时、章动、岁差四方面的修正。其中三个过渡坐标系依次为瞬时地球坐标系、瞬时真天球坐标系、瞬时平天球坐标系。
经上述过程,用Matlab 软件编程后,可以实现从WGS84 坐标系转换到J2000.0 坐标系下的坐标变换。从J2000.0 坐标系转换到WGS84 坐标系是上述过程的逆变换。经与国内“洞察者”卫星软件、卫星导航系统坐标转换软件、STK 软件相比对,转换的位置精度可达0.1m,速度精度可达0.001m/s。
3 卫星轨道预报方法和流程
如前文所言,卫星轨道预报的意义是为星上任务设备提供卫星姿态参考,其内容包括对此后一段时期的卫星位置、速度的预报。具体选择哪一种预报算法取决于星上的计算资源情况,需要在计算资源和预报精度之间取得平衡,从而得到合适的预报结果。
卫星轨道预报的方法分为解析法和数值法等。文献[3]详细论述了二体运动的解析解,并针对第一类无奇点根数提出了简化的J2项摄动的解析解,取得了不错的应用效果,特别是在星上计算资源有限的情况下,能够在要求的精度内预测卫星轨道。
文献[1]则从卫星轨道的瞬时根数出发,推导出了一种更为通用的卫星轨道预测方法,其精度也比文献[3]显著提高,但对于第一类无奇点根数则无法取得令人满意的预测结果。
如此,可采取了多次上注、根据实际轨道精度需求选取合理的上注频次。
4 基于J2 摄动项的Runge-Kutta、Hermite数值轨道预报方法
4.1 基于J2摄动项的Runge-Kutta 数值轨道预报方法
为得到更高精度的卫星轨道预测结果,相比之下,数值方法能够取得更为理想的结果,即间接引用泰勒展开,用积分区间上若干右函数值的线性组合确定相应的系数。一般来说,4 阶Runge_Kutta就能够取得较高的精度要求。现推导如下。
在J2000.0 坐标系下的笛卡尔坐标系中,设递推量rn的表示方式为
各项分别表示卫星当前的三维位置和三维速度信息,其递推公式为
其中h 为积分步长,ki(i=1,2,3,4)为过程变量,其表达式为
式(3)中的f函数输出为
其中,μ为地球引力常数,取3.986×1014m3/m2,。
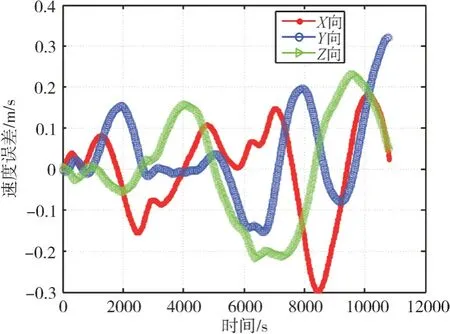
其中J2为地球两次带谐系数,取1.082×10-3,Re为地球平均半径,取6378137m。由此可递推得到卫星轨道的位置、速度信息。基于J2摄动项的Runge-Kutta数值预报如图1、图2所示。
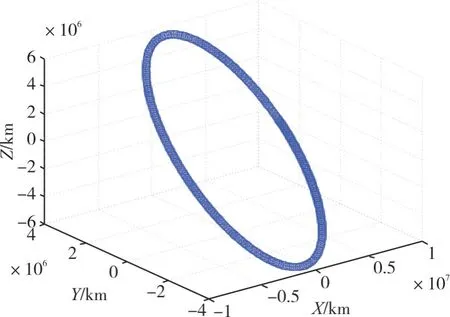
图1 基于J2摄动项的Runge-Kutta数值位置预报
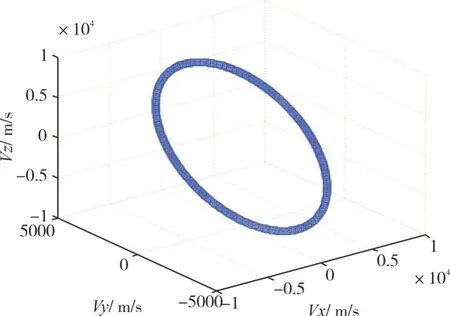
图2 基于J2摄动项的Runge-Kutta数值速度预报
4.2 基于Hermite数值轨道预报方法
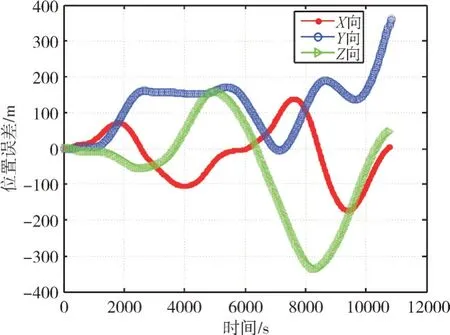
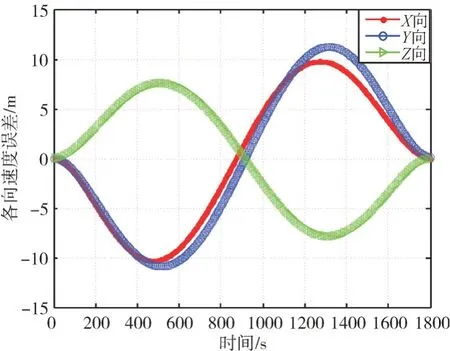
设t0+nh时刻(0 对n分别求一次导、二次导: 分别令n=0,n=1,则有 回代到式(7),则有 对式(12)中n求导,有 其中: 由此可递推得到卫星轨道的位置、速度信息。基于Hermite数值卫星轨道预报如图3、图4所示。 图3 基于Hermite数值位置预报 图4 基于Hermite数值速度预报 以STK 软件的HPOP 算法为真值,对基于J2摄动项的Runge-Kutta 数值轨道预报误差分别如图5、图6 所示,基于Hermite 数值轨道预报误差分别如图7、图8所示。 图5 基于J2摄动项的Runge-Kutta数值位置预报误差 图6 基于J2摄动项的Runge-Kutta数值速度预报误差 图7 基于Hermite数值预报位置误差 图8 基于Hermite数值预报速度误差 由图5、图6 可以看出,基于J2摄动项的Runge-Kutta 数值位置预报各向误差在12000s 内均不超过350m,基于J2摄动项的Runge-Kutta 数值速度预报各向误差在12000s 内均不超过0.4m/s。同样以STK 软件的HPOP 算法为真值由图7、图8 可以看出,基于Hermite 数值位置预报误差在1800s 内各向最大值约为6000m,基于Hermite 数值速度预报误差在1800s 内各向最大值约为12m/s,且呈“钟形”发散。由此可见基于J2摄动项的Runge-Kutta数值预报精度远高于基于Hermite 数值预报精度,实际使用时根据需要选择合适的预报算法。 本文分析了WGS84 坐标与J2000.0 系下的坐标互换,并重点研究了基于J2摄动项的Runge-Kutta 数值预报、基于Hermite 数值预报的方法、精度等。一般来说,卫星轨道预报的数值计算方法的精度远高于解析方法,而且避开了第一类奇点导致的预报精度恶化现象[4~5],但精度要求不高及计算资源有限时,解析方法亦不失为一种分析卫星轨道特性的重要工具,比如计算轨道六根数的变化规律等,这也是下一步继续努力的方向。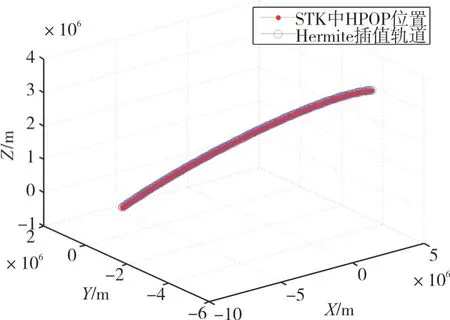

5 轨道预报误差分析

6 结语

