基于POD 方法的EPR 燃料棒流致振动特性分析1)

闵光云 冯琳娜 姜乃斌 ,

* (中山大学中法核工程与技术学院,广东珠海 519082)

† (中国核动力研究设计院核反应堆系统设计技术重点实验室,成都 610213)

引言

承受轴向或横向流的结构常见于能量产生和转换的行业中[1-2],限制这些结构的发展和可靠性的一个重要原因是流体-结构耦合的振动,通常被称作流致振动[3](flow-induced vibration,FIV).FIV 是造成燃料棒包壳微动磨损(grid-to-rod fretting,GTRF)最主要的原因之一[4-5],在工程中需时刻注意.燃料棒包壳容纳燃料芯块,并包容裂变气体,它是防止放射性物质外泄的第一道屏障[6].然而,GTRF 磨损会使得包壳变薄,严重时可能会造成放射性物质泄漏,严重影响国民经济、危害人民安全.

近20 年来,国内外学者在燃料棒流致振动机理及GTRF 磨损领域开展了大量的研究[7-15].部分学者采用数值模拟方法研究燃料棒的流致振动,学者们通常只借鉴“弱流固耦合”思想,即只考虑流场对结构的影响,并没有考虑结构变形对流场的影响.如Kim 等[7-9]建立了燃料棒的多跨连续简支梁模型,结合半经验公式并基于随机振动理论,系统地研究了格架失效对燃料棒固有频率和振型的影响.齐欢欢等[10-11]也通过多跨连续梁模型研究了格架失效对燃料棒湍流激振和旋涡脱落的影响.然而,“弱流固耦合”会乐观地估计燃料棒的换热能力[12],因此考虑流场与结构的双向耦合,实时更新结构和流场的数据是非常必要的,但对计算机的性能要求较高.陈德奇等[13-14]通过3D 建模软件UG 建立了带格架的5×5燃料棒束模型,并通过ICEM 进行了网格划分,最后基于ANSYS-Workbench 中的system couple 模块实现了燃料棒和流场的双向耦合,系统地研究了燃料棒束的流致振动特性.马玉琢等[15]在文献[14]的基础上,进一步考虑了流场-结构场-温度场多物理场耦合效应下燃料棒束的流致振动特性.也有部分学者通过试验手段研究燃料棒的流致振动特性,但试验成本高且工况单一.因此,性价比低、经济性差是限制通过试验手段研究燃料棒流致振动特性的主要原因之一.

另外,在计算流体力学(computational fluid dynamics,CFD)研究中,基于试验或仿真数据样本,构建降阶模型(reduced-order model,ROM)是一种重要的研究手段.目前存在两类典型的降阶模型[16-17]:基于系统辨识方法的ROM (如神经网络模型)和基于流场特征提取方法的ROM (如本征正交分解(proper orthogonal decomposition,POD)).有关POD 的研究,寇家庆等[18]基于POD 方法研究了OAT15A 翼型的跨声速抖振模态;李凯等[19]发展了一种基于POD和Kriging 模型的定常气动力降阶模型,针对三维机翼模型的结果证明了该方法的可行性;孙翀等[20]基于POD 方法研究了风力机翼型在失速工况下的非定常流场特性;郭子漪等[21]基于POD-Galerkin 降维法构建了低维模型,系统地分析了热毛细对流分岔.魏代同等[22]基于POD 方法对叶片碰摩响应问题进行了求解;李玉韦等[23]基于POD 方法求解了加筋筒壳的结构动力响应.Wang 等[24]基于POD-ROM模型系统地研究了黏弹性流体的流动特征.余波等[25]基于POD-RBF 方法对管道内壁进行几何识别.基于POD 方法搭建降阶模型,能够实现振动特性的快速预测,为燃料棒的流致振动行为研究提供了新的研究手段.

目前,国内外公开文献针对(European pressurized reactor,EPR)压力容器内部流场的研究较多,但对于EPR 燃料棒的振动响应仍未有相关研究公开发表.基于此,本文将系统地研究EPR 燃料棒的振动特性.EPR 燃料棒相比M310 燃料棒的棒长更长,导致其频率降低且幅值增大,在冷却剂的作用下,可能会加剧GTRF 磨损,造成放射性物质的泄漏.本文基于ANSYS-APDL 建立了带格架的EPR 燃料棒的多跨连续简支梁模型,系统地研究了格架失效对EPR燃料棒频率、模态的影响.然后,基于全阶模型的样本数据形成快照(snapshots)矩阵,利用POD 方法搭建了ROM,该ROM 能够对模态、湍流响应快速重构.本文研究结果对EPR 燃料棒流致振动特性研究有一定的参考价值.

1 POD 分解

1.1 快照矩阵生成

POD 方法是在全阶模型试验数据或者仿真数据的基础上形成快照矩阵[26-29],然后将快照矩阵投影到低维度的空间,该空间满足快照矩阵的分散程度最大,数学解释即为方差最大.

POD 方法的快照矩阵Y可描述为

式中,y1到yn为不同工况下的样本数据.

1.2 POD 分解及最优基底获取

POD 的本质是在全阶模型试验数据或者仿真数据的基础上,获得一组最优正交基底

寻找全阶系统的最优正交基等价于1 个最值问题

式中,向量 φ 为POD 模态正交基,矩阵 ϕ 是POD 模态正交基的组合,并且矩阵 ϕ 满足式(4)所示的正交性.式(3)中表述的最值问题可以转化为特征值求解问题

由于快照矩阵Y的行号通常会远大于其列号,那么矩阵YYT的维数也会远大于矩阵YTY的维数.因此,为了降低本征正交分解过程中的计算规模,可以定义相关矩阵R

首先通过求解相关矩阵R的特征值和特征向量

进而得到矩阵YYT的特征值对应的特征向量

由此,得到一组POD 模态正交基,且任意样本数据都可以表示成这组POD 模态基的线性组合,即

式中,αi为POD 模态基的系数.

利用上述式(8)获得的少数几个POD 模态正交基可实现对原始全阶模型进行自由度缩减.

为了选择尽可能少的POD 模态正交基,可以通过子空间的总能量与全阶空间能量之比I(h)进行模态截取,I(h)可以表述为相应POD 模态特征值和与全部特征值和的比值

一般I(h)的值应大于90%以上,这样所截取的POD 模态基可以用于将全阶模型投影到更低维的子空间,并且保证一定的精度.

2 数值计算对象与方法

2.1 燃料棒-格架模型

目前,中国台山的EPR 机组可选择使用两种燃料组件,一种是西门子设计的HTP 型燃料组件,另一种被采用的是法国阿海珐(AREVA)设计的AFA-3G LE 型燃料组件.

AFA-3G LE 型燃料组件的设计基于AFA-3G L 型燃料组件[30],每个燃料组件有265 根燃料棒和24 根导向管,呈17×17 的方式排布.AFA-3G LE型的燃料组件全长4802 mm,共有11 个格架,其中8 个为带有搅混翼的搅混格架,另外3 个为不具有搅混功能的定位格架.该型燃料组件底部的2 个格架为定位格架,格架之间的距离较近;再往上为8 个搅混格架,最后1 个定位格架在燃料组件的顶部,详见图1 所示[30].

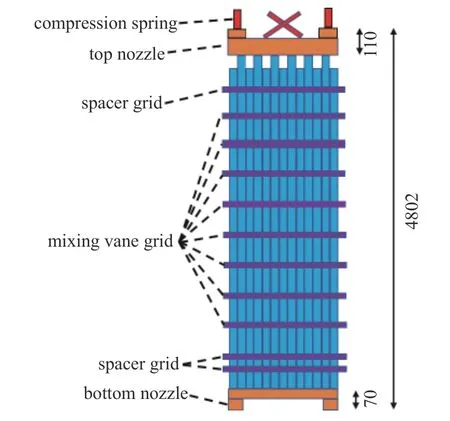
图1 AFA-3G LE 燃料组件示意图 (单位:mm)Fig.1 Schematic of AFA-3G LE fuel assembly (unit:mm)

AFA-3G LE 燃料组件的燃料棒由下部端塞、上部端塞、燃料芯块、弹簧、包壳管和支撑管等部件组成.核反应堆运行过程中燃料棒内部的压力和包壳的应变可能发生变化(辐照蠕变、热膨胀或核裂变过程中会产生气体).因此,在包壳的顶部和底部保留了气腔室,且燃料芯块由弹簧压紧,详见图2所示.

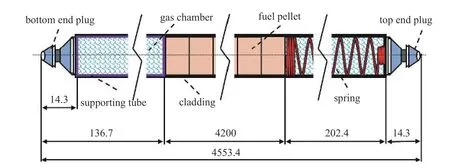
图2 EPR 燃料棒示意图 (单位:mm)Fig.2 Schematic of the EPR fuel rod (unit:mm)

AFA-3G LE 燃料组件中每个燃料棒的长度为4553.4 mm,包壳的外径和厚度分别为9.5 mm 和0.57 mm.格架作为保持燃料棒稳定性和提高其刚度的弹性构件,其由多个相互焊接的Zr-4 合金条带组成.

如图3 所示,在格架位置处,每个燃料棒由2 个弹簧片和4 个刚凸约束,保持了燃料棒的稳定性.

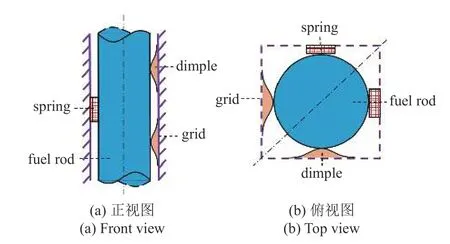
图3 燃料棒受定位格架约束的示意图Fig.3 Schematic of a fuel rod constrained by grid

单根燃料棒受到2 个弹簧片和4 个刚凸的约束,并且这些约束沿格架的对角线对称.本文将刚凸和弹簧等效于弹性约束,如图4 所示.

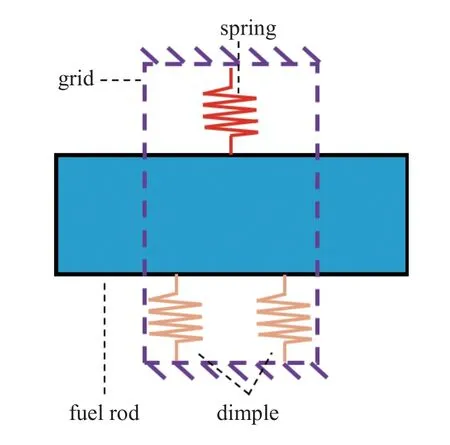
图4 弹性约束示意图Fig.4 Schematic of elastic constraints

综上,单根燃料棒可以简化为多跨连续简支梁模型.

燃料棒的简化模型如图5 所示,在燃料棒每个格架位置处都有弹性约束.

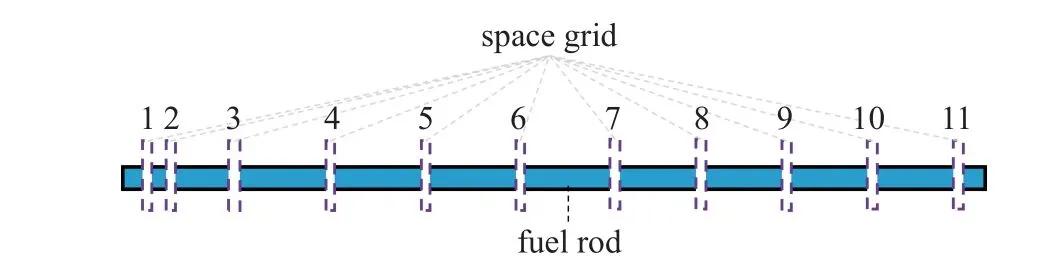
图5 EPR 燃料棒的多跨连续简支梁示意图Fig.5 Schematic of a multi-span continuous simply supported beam of EPR fuel

2.2 湿模态分析

放置在压力容器冷却剂中的燃料棒是典型的流固耦合(fluid-structure interaction,FSI)结构.对于FSI 结构,由于流体和结构之间的耦合效应,模态分析更加复杂.然而,湿模态分析考虑了流体和结构耦合效应.对于FSI 模型,其控制方程可以写成

式中,MS,CS和KS分别是结构的质量矩阵、阻尼矩阵和刚度矩阵;Ma,Ca和Ka分别是流体对结构附加的质量矩阵、阻尼矩阵和刚度矩阵;Fm(t)和Fe(t)分别为与运动相关和运动无关的流体载荷;X是广义位移;(·)表示对时间求导数.

当流速远低于临界流速且结构振幅很小时,流体附加刚度和附加阻尼可以忽略,仅考虑流体附加质量的影响,强耦合问题退化为单向弱耦合问题:考虑附加质量的流固耦合系统强迫激振问题.

EPR 燃料棒为多点支撑系统.在多点支撑作用下,此类系统的临界速度通常很高,即运行流速通常远低于临界流速.同时,多点支撑意味着支撑之间的管段较短且刚度较高,系统不易发生大幅值振动,即系统满足小变形假设.基于以上两点分析,本论文采用单向耦合计算方案分析燃料棒的流致振动特性.流体附加质量等于每个燃料棒排开水的质量,本论文以密度修正方式体现到梁模型中.

根据式(11)进一步可得到

式中,Mc=MS+Ma,Cc=CS,Kc=KS.

对于不考虑阻尼效应的自由振动,式(12)可简化为

式中,ω为固有频率,ψ为振型.

将式(14)代入式(13)可得到湿模态分析的特征方程

本文采用ANSYS-APDL 对燃料棒进行湿模态分析.

2.3 湍流激振响应分析

工程上,通常采用湍流激励响应半经验公式计算燃料棒的湍流激振响应值.根据压水堆燃料棒的结构和流场分布特征,采用功率谱密度表征湍流激励,结合相关功率谱密度试验参数,求解每阶模态的振动位移均方值.

根据文献[31],对于第i阶模态,在x处由轴向流产生的燃料棒均方根振幅为

对于第i阶模态,在x处由横向流产生的燃料棒均方根振幅为

式(16)和式(17)中的物理参数可参考文献[31].

把轴向、横向流产生的振幅线性叠加,则有

式中,σi(x)为第i阶模态的振幅.总振幅由每个模态的振幅组合求得,模态组合采用10%频率组合将各振型组集在一起[31].由每个振型的振幅σi(x)组合得到总振幅σ(x),在节点x处总振幅可表示为

式中,βij为组合系数,如果频率之间的相对偏差小于10%,那么βij=0.5,否则βij=0.

3 POD分解与结果分析

3.1 EPR 燃料棒的流致振动

本文基于ANSYS-APDL 进行湿模态分析.燃料棒是典型的细长结构,其变形主要为梁式变形,因此本文将燃料棒简化为受约束的多跨连续简支梁模型,使用Beam4 单元模拟燃料棒,使用Combine40单元来模拟弹簧、刚凸与燃料棒之间的夹持作用.

由于本文建立的EPR 燃料棒简化模型是结构高度对称的模型,因此其模态是成对出现的,即X-Z平面和X-Y平面的模态是一样的,如图6 所示.

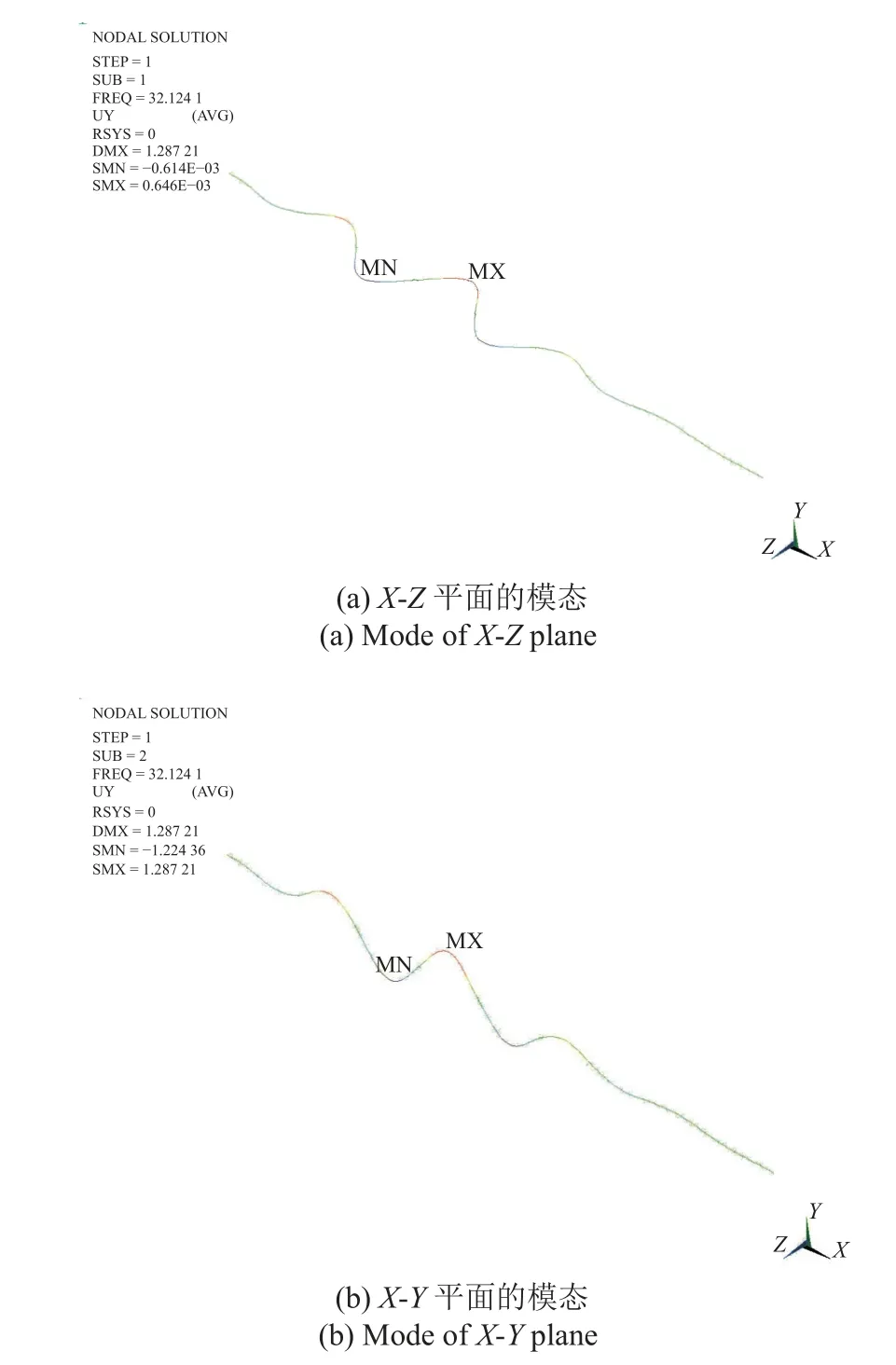
图6 燃料棒的1 阶模态Fig.6 1th-order mode of fuel rod

图6 仅列出了没有格架失效时EPR 燃料棒的1 阶模态.在本文建立的有限元模型下,当模态阶次为16 时,有效质量系数接近1.为了节约篇幅,下文的分析都是基于X-Y面.

在燃料棒的设计过程中,除了考虑燃料棒的材料特性和结构特征外,还需确定格架上弹簧片和刚凸对燃料棒夹持力的大小.夹持力太小时,燃料棒和格架之间的GTRF 磨损将增加;夹持力太大时,燃料棒将因过度约束而产生变形.

本文分析了格架失效对燃料棒湿模态和湍流激振响应的影响,且在本文中,认为格架失效为图3 中格架处的弹性支撑全部失效,即格架中所有的弹簧和刚凸都失去了对燃料棒的弹性约束.本文设定了12 个失效工况,用于EPR 燃料棒的湿模态分析和湍流激振响应分析,相应的12 种失效工况如表1 所示.

表1 失效工况Table 1 Failure working conditions

气腔室不具备刚度,燃料芯块是一块一块堆叠起来的,也不具备刚度.因此本文在建立燃料棒有限元模型时,认为燃料棒的刚度特性主要由燃料包壳提供,即其他部件对刚度的贡献很少,不考虑刚度,但需考虑质量.将其他部件的质量折算入对应的包壳管材料密度中可得到湿模态分析、湍流激振响应计算所需的质量参数,详见表2.此外,杨氏模量为76.9 GPa,泊松比为0.37.

表2 质量参数Table 2 Mass parameter

在上述12 种失效工况下,通过对燃料棒的湿模态分析,得出格架失效对湿模态1 阶模态的影响.以X-Y平面的为例,如图7 所示,其中虚线表示没有格架失效时燃料棒的固有频率.同样,在本文建立的有限元模型下,当模态阶次为16 时,有效质量系数接近1,但由于格架失效对第2 阶到第8 阶模态的影响远低于1 阶,因此这里只列出了1 阶固有频率(图7中的数值为频率的大小).

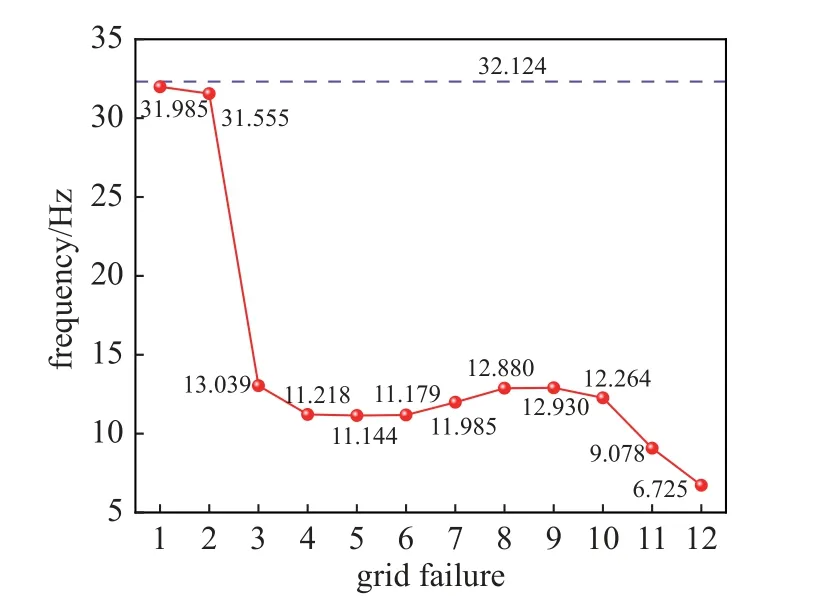
图7 格架失效和无格架失效下的1 阶固有频率Fig.7 1th-order frequency under grid failure and no grid failure

观察图7 可得知,格架失效对燃料棒1 阶固有频率的影响非常显著.第1 个和第2 个格架单独失效时燃料棒的固有频率降低不明显,这是因为这两个格架紧邻,其中1 个格架失效时还有另1 个格架提供支撑刚度.但第1 个和第2 个格架同时失效时,燃料棒的固有频率将大幅度下降.另外,第11 个格架失效时,燃料棒的固有频率也非常小.这两个情况下燃料棒的固有频率非常小的原因是:格架失效时,结构刚度大幅降低,有限元模型也变为悬臂梁模型.

基于湿模态分析所得模态信息,结合式(16)到式(19)可得到格架未失效时燃料棒的湍流激振响应,如图8 所示.图8 中的纵坐标为振幅,横坐标为燃料棒轴线的标高.

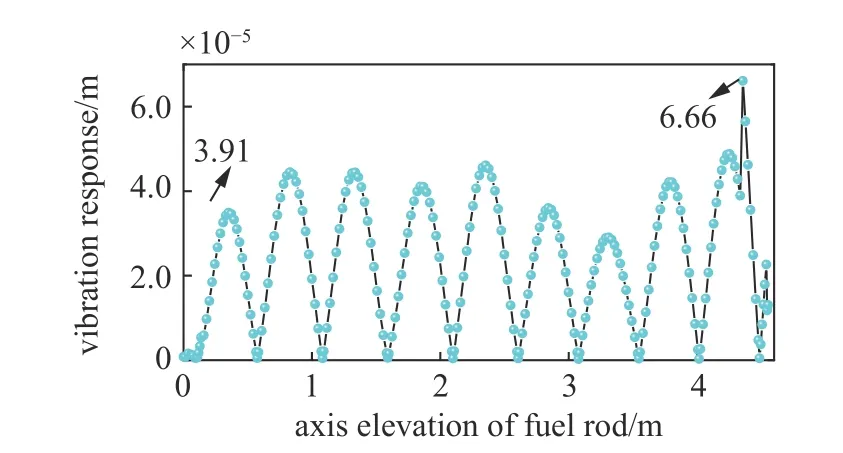
图8 EPR 燃料棒的湍流激振响应Fig.8 Response of EPR fuel rod

图8 的主要作用是为了与下面格架失效时燃料棒的湍流激振响应作对比.格架失效对燃料棒湍流激振响应的影响将在下文详细讨论.

3.2 湿模态分析的POD 降阶模型

基于全阶模型对EPR 燃料棒进行模态分析,得到12 格架失效工况下燃料棒的模态信息并形成快照矩阵Y.根据本文中第1 节介绍的POD 方法将快照矩阵进行POD 分解,得到最优的POD 基,前12 阶POD 模态的特征值λ(线性坐标)见图9.

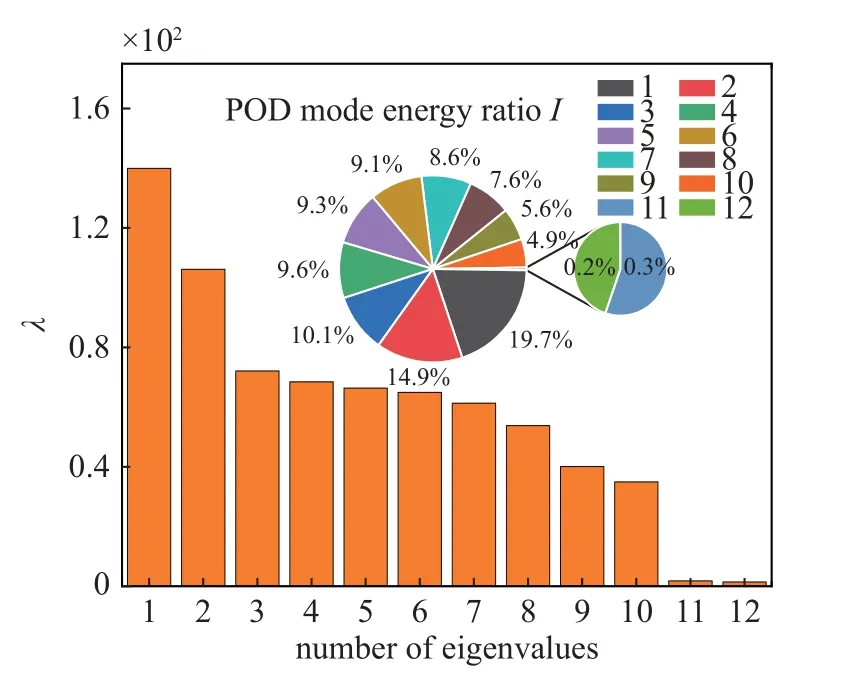
图9 前12 阶POD 模态对应的特征值Fig.9 Eigenvalues of the first 12 POD modes

根据式(10) 计算的模态能量占比I进行POD 模态的截断.如图9 可知第1 阶POD 模态能量占比为10.1%,第2 阶POD 模态能量占比为9.6%;第3 阶到第8 阶的POD 模态能量占比相差不大,都在9%左右,与第1 和第2 阶POD 模态能量占比的差异不是很大.实际上,对于POD 方法来说,前2 阶POD 模态能量占比应该是远远大于后2 阶的POD 模态能量占比,这里出现这个现象的根本原因可解释为ANSYS-APDL 在计算湿模态时导出的模态信息是“归一化”后的模态数据,因此得到的快照矩阵在空间上的分布上是比较均匀的.

为保证降阶模型的计算精度,截取前8 阶POD 模态作为投影子空间 ϕ=[φ1,φ2,····,φ8],将全阶模型投影到由POD 基所展成的子空间中,从而达到模型降阶目的,最后重新投影回原始的物理空间重构EPR 燃料棒的湿模态.将格架失效后,全阶模型和POD 降阶模型所得湿模态进行对比,评估POD降阶模型的计算精度.

本文通过湿模态分析,发现格架失效会对EPR燃料棒的1 阶模态产生明显的影响,且这种影响是具有规律的.为了便于分析,本文只列出了格架失效后燃料棒的1 阶模态,如图10 所示.

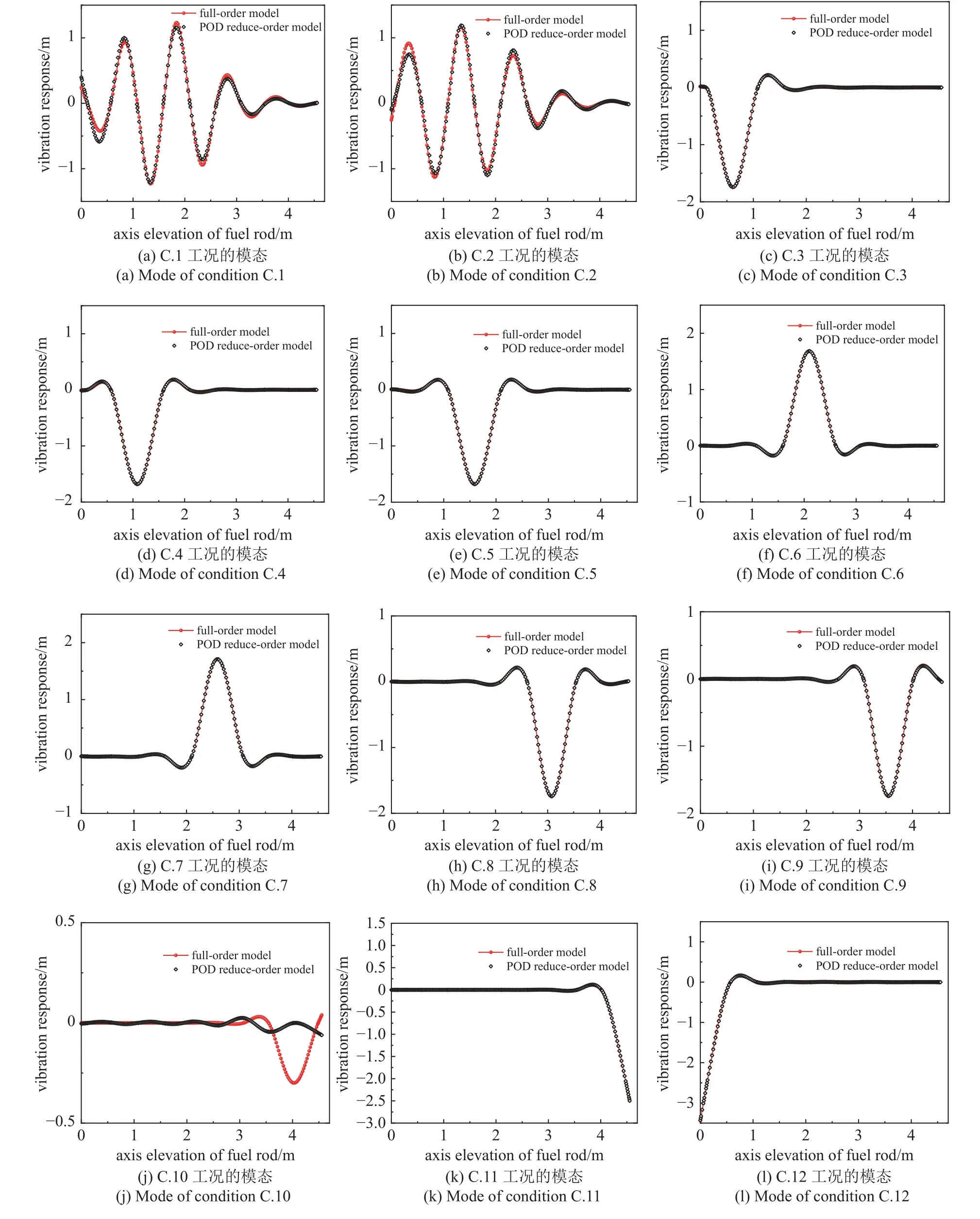
图10 EPR 燃料棒的1 阶模态Fig.10 1th-order mode of EPR fuel rod

观察图10 得到:湿模态的幅值会在格架失效位置处突然变大.8 阶截断的POD 降阶模型基本能够完全重构大部分失效工况下燃料棒的湿模态,但对于第10 工况下燃料棒的湿模态的重构误差较大,需要增加截断阶次.但继续增加阶次将使得降阶效果不明显,这主要是模态数据“归一化”导致的.

3.3 湍流激振响应的POD 降阶模型

基于全阶模型对EPR 燃料棒进行湍流激振响应分析(前8 阶模态响应的叠加),得到12 个格架失效工况下燃料棒的湍流激振响应,并形成快照矩阵Y.接着,根据本文中第1 节介绍的POD 方法将快照矩阵进行POD 分解,得到POD 正交基,前12 阶POD 模态的特征值λ(对数坐标)见图11.

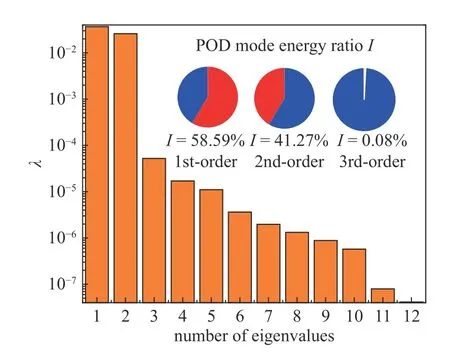
图11 前12 阶POD 模态对应的特征值Fig.11 Eigenvalues of the first 12 POD modes

根据式(10)计算的模态能量占比I进行POD模态截断.如图11 可知第1 阶POD 模态能量占比为58.59%,第2 阶POD 模态能量占比为41.27%,第3 阶POD 模态能量占比为0.08%.观察湍流激振响应的POD 模态能量占比图,可以明显看到前2 阶模态能量占比远大于后2 阶的模态能量占比.

对于湍流激振响应分析,为保证降阶模型的计算精度,截取前2 阶POD 模态作为投影子空间 ϕ=[φ1,φ2],将全阶模型投影到由POD 正交基所展成的子空间中实现模型降阶,最后在物理空间重构湍流激振响应.12 个格架失效工况下燃料棒的湍流激振响应如图12 所示.

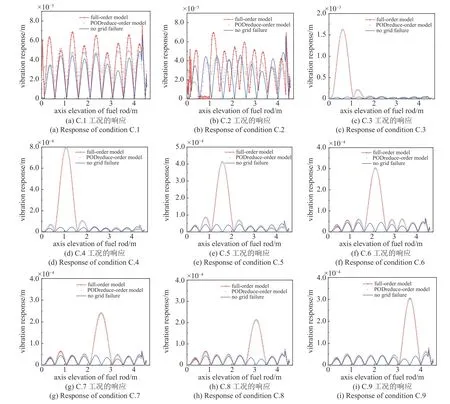
图12 EPR 燃料棒的湍流激振响应Fig.12 Response of EPR fuel rod

观察图12 得到:湍流激振响应会在格架失效位置处突然增大,这主要是因为格架失效会导致燃料棒的局部刚度减小.第11 和第12 工况下燃料棒的湍流激振响应非常大,因为这两个工况下燃料棒的简化模型将变为悬臂梁模型.此外,第3 和第10 工况下燃料棒的湍流激振响应也比较大,工程中也值得注意.

基于2 阶截断的POD 降阶模型能够重构大部分失效工况下的湍流激振响应,但对于第1 和第2 个格架失效时燃料棒湍流激振响应的重构误差较大;对于第1 和第2 个格架失效时燃料棒湍流激振响应的重构需要增加截断阶次.但第1 和第2 个格架失效时燃料棒的湍流激振响应非常小,对结构的危险性是非常低的.

4 结论

本文以EPR 燃料棒为例,系统地研究了格架失效对燃料棒频率、湍流激励响应的影响,得到以下结论.

(1) 格架失效对燃料棒1 阶固有频率的影响非常显著.其中,第1 个和第2 个格架同时失效、第11 个格架失效时,燃料棒的固有频率明显低于无格架失效的固有频率.

(2) 格架失效会导致局部的刚度减小,因此格架失效会使得燃料棒的固有频率降低,且在格架失效处,燃料棒的湍流激振响应会明显增大.

(3) 第1 个格架和第2 个格架同时失效、第11 个格架失效时,燃料棒的湍流激振响应非常大.此外,第3 个格架、第10 个格架失效时,燃料棒的湍流激振响应也比较大.

(4) 对于湍流激振响应分析,POD 方法能降低样本维度,截取前2 阶POD 正交基形成的降阶模型基本能重构燃料棒的湍流激振响应.对于湿模态分析,前8 阶POD 降阶模型才能基本重构燃料棒的湿模态.

(5) 增加燃料棒的支撑刚度以及增加格架的数量能有效地降低EPR 燃料棒的激振响应,工程中应当注意.