基于流固耦合的压气机转子叶片非同步振动分析1)

汪松柏 霍嘉欣 赵 星 陈 勇 2) 吴亚东 张 军

* (上海交通大学机械与动力工程学院,上海 200240)

† (中国航发四川燃气涡轮研究院,成都 610500)

引言

压气机叶片的流致振动问题涉及气体动力学和结构动力学,是航空发动机中典型的流固耦合问题.低成本和轻量化设计要求使得压气机单级气动负荷不断提高,结构上普遍采用轻质低阻尼的整体叶盘设计,这一设计趋势在提高部件性能的同时,也使得叶片气动弹性问题越来越突出,国内外主要航空发动机公司在新型发动机压气机的研制过程中均遭遇过一类新的气动弹性问题——非同步振动(nonsynchronous vibration,NSV)[1-5].非同步振动通常发生在风扇/压气机进口级的非设计转速工况,表现为叶片振动频率与转频不同步,呈非整数倍关系,并具有锁频特征.由于不稳定流体与叶片之间相互耦合,可产生较大的振动应力,常导致叶片高周疲劳失效甚至引发严重的事故.

转子叶片非同步振动常发生于高负荷压气机的非设计工况.1995 年,Baumgartner 等[6]首次报道了高压压气机第一级转子叶片的非同步振动现象,通过机匣壁面动态压力传感器和叶片表面应变片的综合测试捕捉到叶片的高幅值振动.非同步振动的频率特征就是叶片振动频率与转频呈非整数倍的关系,即两者非同步,认为转子叶尖旋转不稳定涡是诱发叶片非同步振动的主要原因.2003 年,Kielb 等[7]实验研究了GE (General Electric)公司轴流压气机第一级转子叶片非同步振动现象,结果表明第一级转子叶片非同步振动表现为锁频锁相的典型特征.Jüngst 等[8]采用动态压力测试阵列、叶片表面应变片和非接触叶尖定时(blade tip timing,BTT)综合测试手段研究了某1.5 级高速轴流压气机转子非同步振动.在大径向间隙的近失速边界,当频率接近且气动模态和结构模态匹配时,叶片非同步振动现象发生,主要由叶尖间隙泄漏流引发的压力高幅值振荡引起.这种多物理场的综合测试方法,能够开展叶片非同步振动的流固耦合实验研究.由于非同步振动实验测量较难且存在较大的危险性,其机理研究还依赖于有效的物理模型及可靠的数值模拟.

Hollenbach 等[9-11]提出一种两自由度的范德波尔振荡降解模型模拟叶片非同步振动,揭示了非同步振动锁频、极限环振动的典型特征,为非同步振动背后的物理机理研究提供了一种新思路.Gan 等[12-13]采用双向流固强耦合方法对GE 公司某压气机第一级转子叶片非同步振动的锁频机理进行了研究,非同步振动发生时,叶片表现为一阶扭转模态振动,气流激励主导频率与刚性叶片的气流激励频率一致,未发生气流激励频率锁定至叶片一阶扭转固有频率的现象,呈现出气流强迫激起的极限环振动特征.Han 等[14-15]采用叶片强迫运动方式结合动网格技术,数值研究了压气机转子叶尖泄漏流和叶片非同步振动的耦合机制.发现叶片振动幅值和振型对非同步振动锁频有重要的影响,间隙泄漏流和振动频率之间的频差小于1%～1.6%时,可能会出现锁频现象,且锁频区域随振幅的增加而变宽.Zhu 等[16]通过全环的非定常流场数值模拟结合叶片结构的谐响应分析研究了汽轮机末级叶片的非同步振动锁频,结果表明叶片振动节径与旋转不稳定模态数重合时,会发生锁频现象,且叶片非同步振动锁频时振动幅值可达未锁频时的近20 倍.由此可见,非同步振动锁频时可产生较大的振动应力,常导致叶片振动应力超限,对叶片高周疲劳和安全性构成严重的威胁[17-21].

压气机转子叶片非同步振动现象属于气动弹性问题,国内外针对压气机转子叶片非同步振动的产生机制并不完全清楚,尚无统一定论.Thomassin等[22-24]认为非同步振动是因为叶尖射流冲击波和反馈波周期性振荡诱发了叶片的高振幅振动,基于此理论提出一种预测非同步振动发生的临界转速模型.文献[25-31]认为叶尖旋转不稳定性是诱发叶片非同步振动的气流激励源.不管是前缘龙卷涡的运动、间隙泄漏流的周期性振荡,还是泄漏流与分离流间的相互作用,都表现出类似“旋转不稳定性”的特征.然而,由于上述研究结果并未发生显著的叶片振动超限问题,并未对转子叶尖旋转不稳定性与叶片结构响应间的耦合机制作深入探讨.文献[32-34]认为压气机内不稳定涡的声波与叶片共振是非同步振动产生的主要原因.

目前,对压气机内不稳定流动与叶片非同步振动之间的流固耦合机制认识不清,难以指导叶片非同步振动的机理分析及减振设计.本文采用时间推进的双向流固耦合数值仿真方法,对比研究了某1.5 级压气机刚性转子内不稳定气流激励与流固耦合作用下叶片非同步振动的结构响应特征,揭示了压气机转子叶片非同步振动的产生机制,为流固耦合条件下压气机转子叶片非同步振动失效的机理分析及叶片减振设计提供参考.

1 研究对象及数值方法

1.1 研究对象及网格离散

本文以某1.5 级跨声速压气机为研究对象,几何包含进口导叶、转子叶片和静子叶片,叶片数分别为52,47 和68.转子展弦比为1.48,轮毂比为0.74,径向间隙与叶尖弦长比值为0.5%,转子叶片非同步振动的物理转速为9564 r/min.全环非定常流场计算模型和转子有限元模型如图1 所示.流体网格采用IGG/AutoGrid5 生成,叶片周围采用正交性较好的O 型网格拓扑,其他区域采用H 型网格,叶尖间隙采用蝶形网格拓扑,全环模型流体网格节点总数约为3500 万,近壁面第一层网格y+值在15～25 之间.转子固体网格为六面体的结构化网格,采用Solid186高精度实体单元,单个转子叶片单元数为14276.转子叶片材料为钛合金,其性能参数为:密度ρ=4500 kg/m3,弹性模量E=112 GPa,泊松比μ=0.36.

图1 数值计算网格Fig.1 Numerical calculation grid

1.2 流体动力学数值求解

压气机非定常流场通过商业软件CFX 求解三维非定常雷诺平均(unsteady Reynolds-averaged Navier-Stokes,URANS)方程,空间离散采用高精度格式,时间离散采用二阶Euler 格式.湍流模型采用κ-ε 模型,该模型采用自适应壁面函数(scalable)处理边界层,允许叶片近壁面第1 层贴体网格y+较大,避免叶片运动时叶尖流体网格出现负体积,提高流固耦合仿真的鲁棒性和计算效率,众多学者[35-36]采用该湍流模型开展压气机内不稳定流动机理研究.计算工况:转速9564 r/min,轴向进气,进口总温294 K,总压58 kPa,湍流度为5%,出口给定满足径向平衡方程的平均静压,固体边界为无滑移、绝热壁面条件.非定常物理时间步为4.45×10-6s,每个物理时间步内流体域计算迭代8～10 次,每个流体域时间步内固体域迭代6 次,转静交界面选取动静叶滑移边界(transient rotor-stator).

1.3 结构动力学数值求解

每一个时间步内对叶片结构动力学方程进行求解,叶片瞬态动力学方程为

1.4 双向流固耦合方法

为了研究压气机内不稳定流体与叶片非同步振动之间的流固耦合过程,转子叶片非同步振动的流固耦合数值模拟采用流体域和固体域双向耦合迭代方案,如图2 所示.流固耦合计算由内外两个循环控制,外循环控制流固耦合非定常时间推进,内循环控制流体域和固体域交界面上的插值和数据传递,当内循环流体域和结构域的载荷和位移都达到收敛状态时迭代结束,进入下一个物理时间步的外循环.流固耦合的交界面上,采用守恒插值法在每一个时间步内将气动载荷和结构边界的位移等信息在耦合交界面交换以实现流场和结构场信息传递,保证能量传递守恒和几何位移传递守恒,其表达式如下

图2 流固耦合迭代方案Fig.2 Fluid-structure interaction scheme

式中,Fi为固体耦合面上节点载荷;ui为节点位移;pj为流体耦合面上的表面压力;νfi表示流体交界面网格节点运动速度;νsi表示固体交界面网格节点运动速度.

2 刚性叶片结果分析

某发动机高压压气机第一级转子叶片在非设计转速的近失速工况出现非同步振动问题,振动发生时表现为机匣压力脉动的急剧增加,第一级转子叶片振动应力超限,本文针对第一级转子叶片非同步振动发生工况开展数值仿真和分析.

为了揭示转子叶尖不稳定流体与叶片非同步振动之间的耦合机制,首先采用非定常数值模拟对刚性叶片的全环非定常流场进行了数值模拟.图3 为转子不同叶高数值探针静压波动的时间历程和频谱,分别监测了10%,50%和90%叶高前缘点的静压波动.从时程图中可以看出,10%叶高静压波动的幅值较小,其波动幅值约为1.5%.50%和90%叶高静压波动剧烈,90% 叶高最大,其波动幅值可达12.5%.90%叶高监测点波峰静压绝对值为52.1 kPa,波谷静压绝对值为21.2 kPa.对监测点静压波动的时程曲线进行快速傅里叶变换获取频谱信息,从频谱图中可知流场存在非整数倍气流激励频率1.52EO(engine order) 及其谐波频率(3.04EO,4.56EO和6.08EO),且非整数倍气流激励频率幅值较叶片的通过频率幅值大,叶尖区域非整数倍气流激励频率幅值明显较叶根大,表明诱发非整数倍气流激励的不稳定流动出现在转子叶尖区域.

图3 不同叶高数值探针静压波动的时间历程和频谱Fig.3 Time history and frequency spectrum of static pressure fluctuation of numerical probes for different spans

图4 为刚性转子98%叶高截面相对马赫数云图,叶尖区域流场出现明显的周向非均匀性现象,流场的周向非均匀性可影响至压气机进口.转子叶尖吸力面相邻通道出现间歇性分离涡摆动,分离涡的周期性脱落及再附过程导致了叶尖压力的剧烈波动.由于相邻通道的压力波动具有相位延迟,从相对坐标系下观察,叶尖不稳定流体运动与转子旋转方向相反,其绕转子的周向运动从而产生了与转速不同步的气流激励频率.

图4 98%叶高截面相对马赫数分布Fig.4 Distribution of relative Mach number at 98% span

图5 为刚性转子出口相对马赫数分布,叶尖周向存在2～3 个叶栅通道形成的低速区,低速区周向个数为19,为叶尖不稳定流体的周向主模态数.为了进一步分析叶尖不稳定流体的周向空间结构,对不同叶高前缘的周向静压波动分布分别进行空间快速傅里叶变换(spatial fast Fourier transform,SFFT),从而得到周向不同尺度的流场结构数量.从图6 静压波动的SFFT 谐波分析结果可知,叶尖不稳定流场周向主模态数为19 阶,其他2 阶、9 阶和28 阶模态数幅值相对较小.从不同叶高19 阶主模态幅值对比也可以看出,不稳定流动在叶尖的扰动明显比叶根强烈.

图5 转子出口相对马赫数分布Fig.5 Distribution of relative Mach number at rotors exits

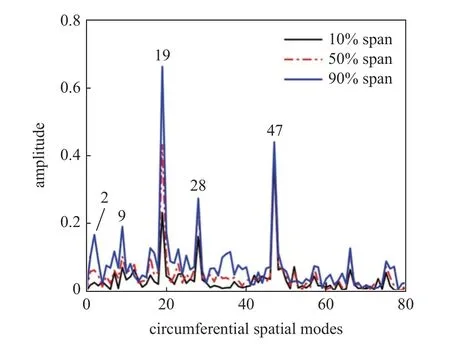
图6 转子前缘静压波动的SFFT 分析Fig.6 SFFT analysis of static pressure fluctuation at rotor leading edge

近失速工况下,压气机仍可以正常工作.图7 为转子叶尖流线图,叶尖低速区主要分为两部分.一部分是由叶尖吸力面分离涡形成的大尺寸低速区,起源于转子70%～80%叶高前缘,分离涡具有明显的三维空间结构,沿径向和周向向机匣壁面发展,其尺度几乎占据了叶尖整个通道,最终向下游运动流出叶片通道.另一部分流线穿过相邻通道的叶尖间隙形成间隙泄漏流,与主流相互作用形成小尺度的低速区.从影响程度看,分离涡的扰动明显较间隙泄漏流强烈,是引起叶尖压力剧烈波动的主要原因.图8为Q准则下叶尖径向分离涡结构,分离涡在空间具有三维“径向涡”结构,起源于叶尖吸力面前中部,向相邻叶片压力面周向运动,结束于机匣壁面,文献[3,37-38]称其为“tornado-like separation vortex”,是突尖波(spike)型失速先兆的一种流动特征.

图7 转子叶尖流线图Fig.7 Streamline diagram of rotor blade tip

图8 Q 准则下叶尖径向分离涡结构Fig.8 Radial separation vortex structure near the tip region using Q-criterion

3 柔性叶片流固耦合分析

本节主要分析流固耦合下柔性叶片的非定常流场、不稳定气流激励及叶片非同步振动响应特征.首先,采用有限元分析软件ANSYS 对转子叶片进行模态分析,转子叶片前3 阶固有频率及振型如图9所示.第1 阶振型为弯曲模态,频率714 Hz;第2 阶振型为扭转模态,频率1564 Hz;第3 阶振型为2 阶弯曲模态,频率2142 Hz.图10 为转子叶片的共振转速图,在第1 级转子叶片发生非同步振动的等转速线上,转子一阶弯曲固有频率714 Hz (4.47EO) 与刚性转子非整数倍气流激励频率的3 倍谐波频率4.56EO 非常接近,两者频差约为1.8%,位于4 阶次和5 阶次激励之间,该频率可提供叶片非同步振动的初始气流激励源.图11 为流固耦合作用下转子叶片瞬态总位移云图分布,叶根至叶尖位移逐渐增大,转子叶片最大位移位置出现在叶尖前缘,叶尖前缘至尾缘位移逐渐减小,位移特征总体符合一阶弯曲模态振型,表明第1 级转子叶片处于以一阶弯曲振型主导的非同步振动.

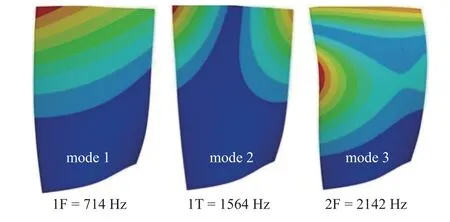
图9 转子叶片前3 阶模态Fig.9 The first three-order of rotor blade

图10 转子叶片共振转速图Fig.10 Campbell diagram of rotor blade

图11 转子叶片瞬态总位移云图Fig.11 Total transient displacement of rotor blades

图12 为转子叶片非同步振动下90%叶高前缘监测点静压波动的时间历程和频谱.转子叶片非同步振动下叶尖静压波动幅值与刚性转子叶尖静压波动幅值相当.气流激励频率为非整数倍的4.47EO和12.23EO 频率,其中4.47EO 为转子叶片的一阶弯曲固有频率,12.23EO 为不稳定流动的气流频率,是由叶片振动导致的非定常流场改变引起.与图3(b)的对比可以看出,具有明显尖峰的非整数倍气流激励频率及其谐波倍频消失,诱发叶片非同步振动的气流激励频率锁定为叶片一阶弯曲固有频率.图13为转子叶片叶尖前缘总位移响应时间历程和频谱.转子叶片非同步振动发作时其响应位移并未发散,总体呈现等幅值的极限环振动特征.振动的位移响应频率为一阶弯曲固有频率,同时可见叶片的一阶扭转固有频率,但其幅值相对较小,即叶片非同步振动以一阶弯曲模态主导,这与图11 中转子叶片瞬态总位移分布特征是一致的.图14 为转子叶片非同步振动叶尖前缘响应的相位图,叶片振动相位图为封闭的环形曲线,振动特征表现为极限环振荡状态,其动力学响应最终呈收敛状态.

图12 非同步振动下数值探针静压波动的时间历程和频谱Fig.12 Time history and frequency spectrum of static pressure fluctuation of numerical probes during NSV

图13 转子叶尖前缘总位移响应的时间历程和频谱Fig.13 Time history and frequency spectrum of total displacement response at leading edge

图14 转子叶片非同步振动响应的相图Fig.14 Phase diagrams of rotor blades during NSV

图15 为转子叶片非同步振动下98%叶高截面的相对马赫数,与图4 刚性转子叶尖相邻通道间歇性分离涡不同,非同步振动下转子叶尖每个通道存在周期性的分离涡,且分离涡位置更靠近尾缘,原先刚性转子通道内间歇性分离涡的流动状态被叶片的极限环振动所胁迫,体现了叶片非同步振动与叶尖不稳定流动之间的耦合作用.图16 为非同步振动下转子出口相对马赫数分布,转子叶尖各通道的流动状态在周向趋于一致,叶尖低速区的周向个数相比刚性转子增加,这与图12 中非整数气流激励频率增加是一致的.

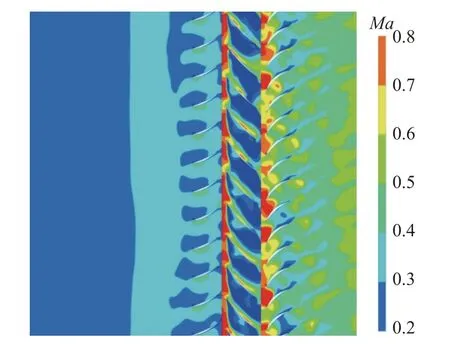
图15 非同步振动下98%叶高截面相对马赫数分布Fig.15 Distribution of relative Mach number at 98% span during NSV

4 结论

本文基于时间推进的方法建立了多级压气机转子叶片全环的双向流固耦合模型,在近失速工况下,对比研究了某1.5 级压气机刚性转子叶尖不稳定流动的气流激励频率与流固耦合作用下叶片非同步振动的结构响应特征,可得出如下结论.

(1) 近失速工况下,转子吸力面径向分离涡是引起叶尖区域压力脉动增大的主要原因,径向分离涡的周期性脱落与再附过程产生了非整数倍气流激励频率,其3 倍谐波频率与叶片一阶弯曲固有频率接近,提供了叶片非同步振动的初始气流激励,诱发了以一阶弯曲模态主导的非同步振动.

(2) 转子叶片非同步振动表现为极限环特征,其动力学响应最终呈收敛状态.基于时间推进的双向流固耦合方法能够获取压气机内不稳定流动与叶片振动之间的耦合关系,可用于分析压气机内复杂的流致振动问题.

(3) 转子叶片的非同步振动会明显改变叶尖不稳定流动,刚性叶片表现为相邻通道间歇性的分离涡结构,非同步振动叶片每个通道均存在周期性的分离涡,且分离涡位置更靠近尾缘.非同步振动发生时,非整数倍气流激励频率及其谐波倍频最终锁定至叶片一阶弯曲固有频率,转子叶尖周向流场被极限环振动所胁迫而趋于一致,体现了不稳定流动与叶片非同步振动之间的耦合.