基于EKF 的GMAW 实时焊缝跟踪研究*

杨园洲 薛瑞雷 刘宏胜 夏 磊

（新疆大学智能制造现代产业学院（机械工程学院），新疆 乌鲁木齐 830017）

GMAW 是碳钢、不锈钢的主流焊接工艺，采用GMAW 自动焊可显著提高生产效率（4～5 倍）[1]。在弧焊过程中，工件与导电嘴间距离（contact-tipto-work distance，CTWD）会使弧长发生变化，通过控制焊接电流可以控制CTWD，让弧长保持稳定，但是由于工件受到自身加工误差、热变形等因素的影响，焊枪无法保持恒定的高度，影响焊接质量[2-3]。

自动焊接的前提是焊缝跟踪，通过声、电和视觉传感器检测焊缝是实现焊缝跟踪的常用方法[4]。声音传感器实时性高，但易受噪声影响，精度较低。视觉传感器精度高，可提前检测焊缝位置，但实时性弱，易受干扰，易引入超前误差。电弧传感器通过下位机进行判断，运算速度快，不受弧光、飞溅和烟尘等于扰，可直接获取焊枪的位置，结构简单，成本低[5]。所以本文选择电弧传感器来实现焊缝跟踪。高延峰等[6]采用比例和参数自调整模糊控制实现焊缝跟踪。洪波等[7]分析磁控电弧信号的频谱，提出了一种基于滑动固定数据窗的电弧信号实时小波降噪方法。张锋等[8]设计了FIR 和一种模糊控制器进行偏差调整。Fabry C 等[9]使用电弧传感和光学测量来控制每个焊道的摆动角幅度、送丝速度和焊接速度的变化。Lei T 等[10]针对环形焊缝多且密集的管板焊接提出了一种基于直流脉冲方波的电弧电压实时跟踪算法与二维和三段模糊控制器。国内外目前在焊缝跟踪方面的研究主要采用模糊控制来实现焊缝的控制，但是精度和运行稳定性还不够。

焊接过程中往往呈现出非线性特性，并且焊接环境中存在的噪声和干扰可能影响焊缝跟踪系统的性能，导致跟踪不稳定。本文通过数学模型法检测焊枪的高度偏差和水平偏差，并通过EKF 算法对焊接偏差进行状态估计，以此完成GMAW 自动化焊接过程中对焊枪的实时精准调节。

1 实验平台

本文是针对图1 所示的坡口进行实验，试验材料为Q235 低碳钢，工件尺寸为长300 mm、宽150 mm、高25.7 mm，填充材料为实心碳钢焊丝，直径为1.2 mm。图2 所示为焊缝跟踪系统的结构图，由GMAW 焊接设备、信息采集设备和控制设备组成。GMAW 焊接设备包括管道焊接工作站、ASM-500 数字化多功能焊机、保值久WRA-300s 焊机循环冷却水箱、送丝机。信息采集设备由J-LK-KT 系列霍尔电流传感器和数据采集卡组成，实现电流信号的采集与存储。控制设备由控制机构和计算机组成，实现启停工作站的引弧以及控制焊枪。焊枪运动轨迹如图3 所示。

图1 焊缝坡口

图2 焊缝跟踪系统结构示意图

图3 焊枪运动轨迹

2 信息采集与处理

2.1 信号预处理

FIR 可以有效滤除高频噪声和干扰，从而减少噪声对焊接信号的干扰，有助于提取焊接质量相关的信号信息。焊接过程中的关键信息通常包含在低频部分，FIR 有助于保留这些低频信号，以进行焊接过程的监测和控制。FIR 主要特点是没有反馈，仅依赖于输入信号的当前和过去的样本，这使得FIR 非常稳定。在FIR 中，较低的阶数可以减少计算量，而较高的阶数可以获得更好的滤波特性，但计算量会相应增加。

FIR 的输出信号可以通过式（1）计算：

式中：y[n]为输出信号的当前样本，x[n-k]为输入信号的当前样本，h[k]为FIR 的第k个系数，N为FIR 的阶数。

图4 所示为采样频率为100 ms，试件向左偏移3 mm 时的原始数据与滤波后的数据对比情况。滤波前，电流波形变化夹杂着随机噪声和尖峰信号；滤波后，电流波形逐步平缓，且随机噪声和尖峰信号逐渐被滤除。波形可反映出电流的变化趋势。

图4 原始数据与滤波后的数据对比图

2.2 焊枪高度检测

高度跟踪是焊接过程中将电流通过FIR 滤波器处理后，利用焊枪高度与电流的数学模型计算出高度偏差，通过EKF 实现焊缝高度跟踪，如图5 所示。

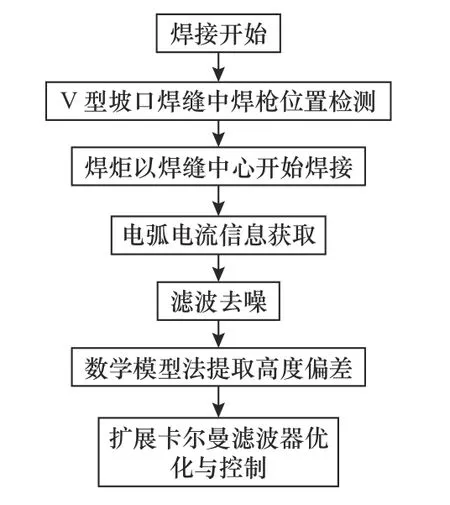
图5 焊缝高度跟踪流程图

焊接过程存在静态特性和动态特性。静态特性指焊接过程中参数不随时间变化。动态特性指焊接过程中的瞬时变化和波动性质。静态特性分析可以用于确定焊接参数的最佳值，以获得最佳的焊接质量；动态特性分析可以用于监测焊接过程，用来发现不良焊缝并采取措施加以纠正。所以本文是针对焊接的动态特性展开的研究，为后续的研究提供贡献。

由于电流随CTWD 的变化而变化，在给定焊接速度和送丝速度的条件下，焊接平均电流和CTWD成正比例关系，其关系可写成式（2）：

式中：H为一个摆动周期内焊枪的高度；I为焊接平均电流；K、b 均为常数。

为了获取K、b 的值，通过采集CTWD 从15 mm变化到20 mm 的电流，将电流分成不同的区间段来求取均值，并通过最小二乘法拟合出H与I的关系，如图6 所示。

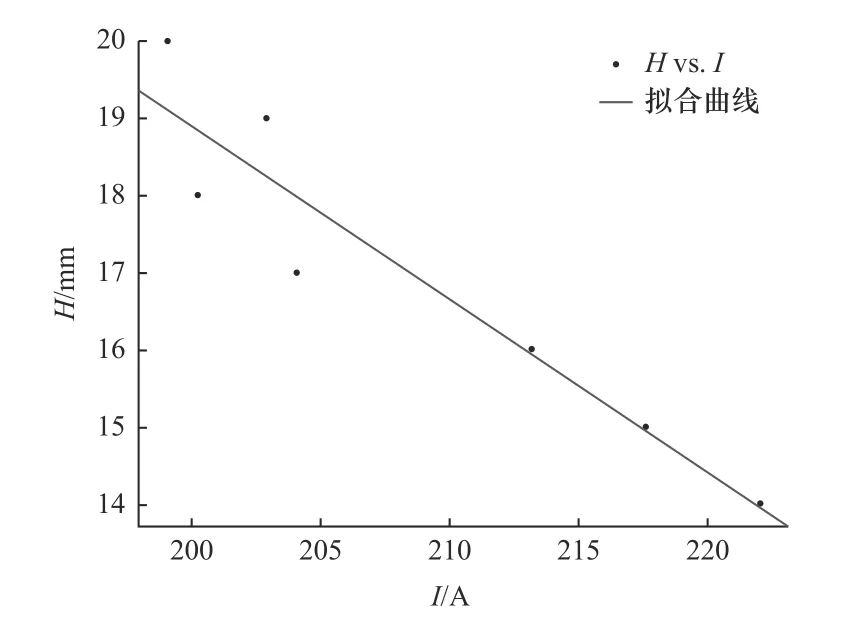
图6 高度跟踪数学模型图

为了避免刚开始时的电弧的稳定状态对焊缝跟踪过程造成偏差，通常会排除焊接开始的2～3 s 内的电流信号值。拟合出的公式如下：

数学模型通过焊枪骤降到3 mm 来验证，焊接电流如图7 所示，焊缝如图8 所示。

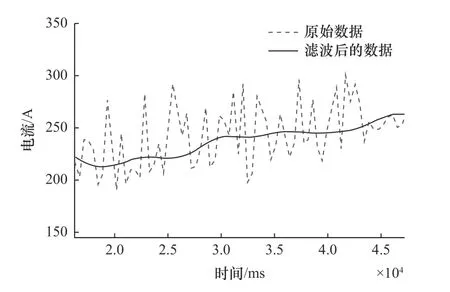
图7 高度跟踪数学模型验证实验电流变化图

图8 CTWD 从15 mm 骤降到12 mm 的焊缝

2.3 焊枪水平偏差提取

水平跟踪是先对电弧传感器提取的电流信息滤波处理，后获取在同一个周期内左右半周期的电流值的积分差，通过EKF 将焊缝偏差电流数值转化为焊枪偏移数据，如图9 所示。

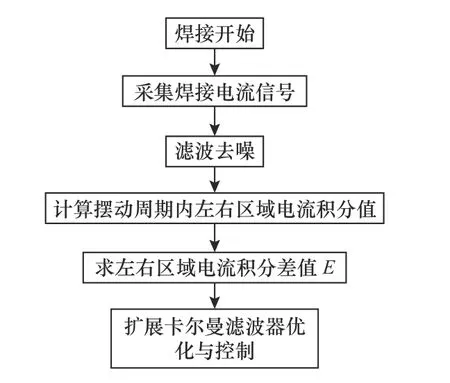
图9 焊缝水平跟踪流程图

从2.2 节高度跟踪的数学模型的研究可知，CTWD 和焊接电流呈线性关系，这是焊缝水平跟踪的理论基础。对于水平偏差提取的算法有多种，如：极限位置电流差值法，此算法简单，但受电弧稳定性影响大；特征谐波检测法可以直接反映焊缝的横向偏差，但对传感器要求较高，且计算复杂；直接测位法计算直观，但需大量比较，精度较低；积分差值法能反映焊缝位置，不受电弧稳定性影响。

本文使用积分差值法计算焊枪偏差，如图10所示，其中焊枪连续两次到达中心位置过程中电流的积分值作为一侧的特征参数，通过式（4）和式（5）计算左右两侧的积分差值，并获取在同一个周期内左右半周期的电流值的积分差，通过式（6）得到水平位置偏差。

图10 积分差值法偏差计算方法

式中：I0、I1分别为焊枪在同一周期内左、右半周期的平均电流值；N为每个摆动周期的采样点数；h为积分步长，h=2π/N。

式中：E为焊枪水平偏差；K为电流积分差和偏差的相关系数，利用最小二乘法拟合后K为0.570 7。

2.4 焊缝跟踪控制算法——EKF

由于焊接系统为非线性时变系统，焊接系统通常涉及焊接温度、电流、电压和速度等。这些变量之间相互作用，使得对整个系统进行建模和控制变得更加复杂。而EKF 是在卡尔曼滤波的基础上，通过线性化非线性系统模型和非线性观测模型来处理非线性的系统和观测方程。对于焊接过程中的非线性系统控制问题，可以使用EKF 来跟踪和估计焊接过程中的状态变量，而且EKF 通常更简单且计算效率较高。此外，焊缝跟踪中传感器通常无法获取全面的信息，获取的信息也常常夹杂着噪声。EKF 可以通过对测量数据进行加权处理，并根据测量数据和先验知识共同更新参数和状态的估计，从而提供准确的数据，以此提高焊接质量，提升焊缝跟踪的精度。

EKF 使用泰勒级数展开来将非线性状态转移方程和非线性观测方程在当前状态估计值附近进行线性化，后对线性化方程进行预测和校正。在EKF的应用中，核心是在EKF 框架下确定系统的状态转移模型和观测模型。算法的步骤如图11 所示。

图11 扩展卡尔曼滤波器算法的运算过程

2.4.1 初始化

2.4.2 时间更新（预测）

（1）利用系统模型对当前状态进行预测，见式（7）和式（8）。根据焊接时的状态空间方程式（9）和测量方程式（10），并通过使用前一时刻的状态估计值和控制输入u[k-1]来预测当前时刻的状态值。

式中：f()为非线性动态方程和非线性测量方程，u[k-1]为输入向量；z[k]=h()为测量方程；过程噪声w～N(0,Qc)，服从正态分布，期望为0，状态协方差矩阵为Qc；测量噪声v～N(0,Rc)，服从正态分布，期望为0，状态协方差矩阵为Rc

（2）利用雅可比矩阵（Jacobian Matrix）线性化系统模型，见式（11）和式（12）。由于系统模型是非线性的，需要通过在当前状态点处对系统模型进行一阶泰勒展开来进行线性化。

2.4.3 测量更新（校正）

（1）利用雅可比矩阵线性化测量模型，见式（13）和式（14）。由于测量模型也是非线性的，需要通过求解雅可比矩阵来近似非线性测量模型。

（2）计算卡尔曼增益K[k]。通过将预测误差协方差矩阵与测量误差协方差矩阵进行加权和的逆矩阵相乘，得到K[k]，用于校正预测误差，见式（15）。

2.4.4 重复执行步骤2 和步骤3

直到所有测量值被处理完毕或达到预设的停止条件。在每个步骤中，每次迭代的先验状态估计是由上一次的后验状态估计通过系统模型进行预测得到的。通过预测和校正的不断迭代，以获得更准确的状态估计。

这些步骤构成了EKF 算法的基本框架，并用于在非线性系统和非线性观测模型的情况下进行状态估计。通过迭代预测和校正步骤，EKF 能够逐步优化对系统状态的估计，并考虑预测误差和测量误差，以获得最准确的状态估计。本文在焊缝跟踪过程中，建立了焊缝位置参数的状态方程和测量方程，并对系统状态进行预测和估计，从而获得准确的焊枪相对焊缝中心的位置，提高了焊缝跟踪的精度。

3 实验验证

3.1 跟踪验证方案

实验方案见表1，焊接位置为平焊区，本文设计了高度、水平和整体跟踪实验来验证算法的稳定性和可行性。高度跟踪试验如图12 所示，通过抬高试件来模型管道焊接时的垂直方向的误差。水平跟踪试验如图13 所示，通过偏移试件来模型管道焊接时的水平方向的误差，水平方向焊枪行走轨迹如图14 所示。高度跟踪实验中，抬高试件一侧4 mm；水平模型验证实验中，偏移试件一侧5 mm；整体跟踪模型验证实验中，抬高试件一侧4 mm，同时偏移试件同一侧5 mm。以上选择的误差均符合焊接工艺中所描述的管道组对坡口偏差不超过管道厚度20%的标准，因为板厚为25.6 mm，则误差为5 mm 以内。焊接时的焊接参数见表2，本文采用固定焊接参数的方式来进行实验，因为焊接参数对焊缝跟踪的影响较大。当焊接参数变化时，焊缝热量也会变化，焊缝边缘容易出现熔池扩大、喷溅等现象，容易出现不良焊缝形状，会影响焊缝跟踪，影响实验的有效性。

表1 试验方案

表2 焊接参数

图12 垂直方向偏离焊缝实验

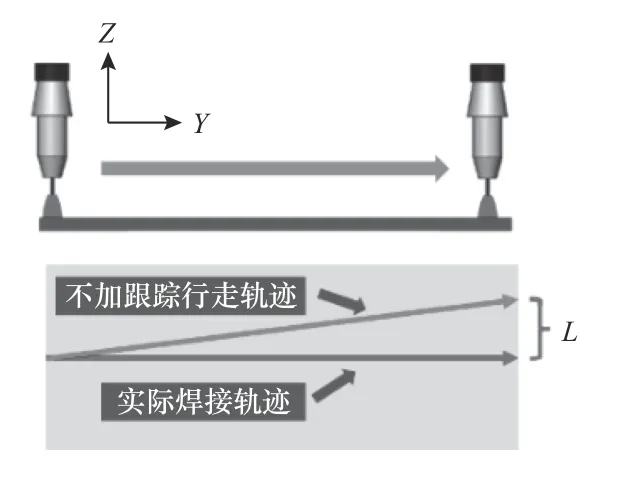
图13 水平方向偏离焊缝实验

图14 实际焊接工件状态

3.2 实验结论

高度跟踪实验中，利用数学模型实现焊枪高度偏差的采集和处理，并利用EKF 实现垂直方向的纠偏。高度跟踪轨迹曲线如图15 所示，焊枪初始高度为15 mm，高度偏差维持在±0.25 mm 以内，焊缝成形图如图16 所示。

图15 高度跟踪轨迹曲线（H=4 mm）

图16 试件一侧抬高4 mm 焊缝图

水平模型验证实验中，利用水平跟踪模型实现焊枪水平偏差的采集和处理，然后利用EKF 实现水平方向的纠偏控制，水平跟踪轨迹曲线如图17所示，水平偏差维持在±0.25 mm 以内，焊缝成形图如图18 所示。

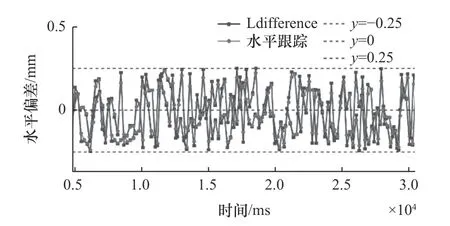
图17 水平跟踪轨迹曲线（L=5 mm）

图18 试件一侧偏移5 mm 焊缝图

整体跟踪模型验证实验中，抬高试件一侧4 mm，偏移试件同一侧5 mm，之后利用整体跟踪模型实现焊枪高度和水平偏差的采集和处理，然后利用EKF 实现垂直和水平方向的纠偏控制，高度和水平跟踪轨迹曲线如图19 所示，焊枪初始高度为15 mm，高度偏差和水平偏差维持在±0.25 mm 以内。

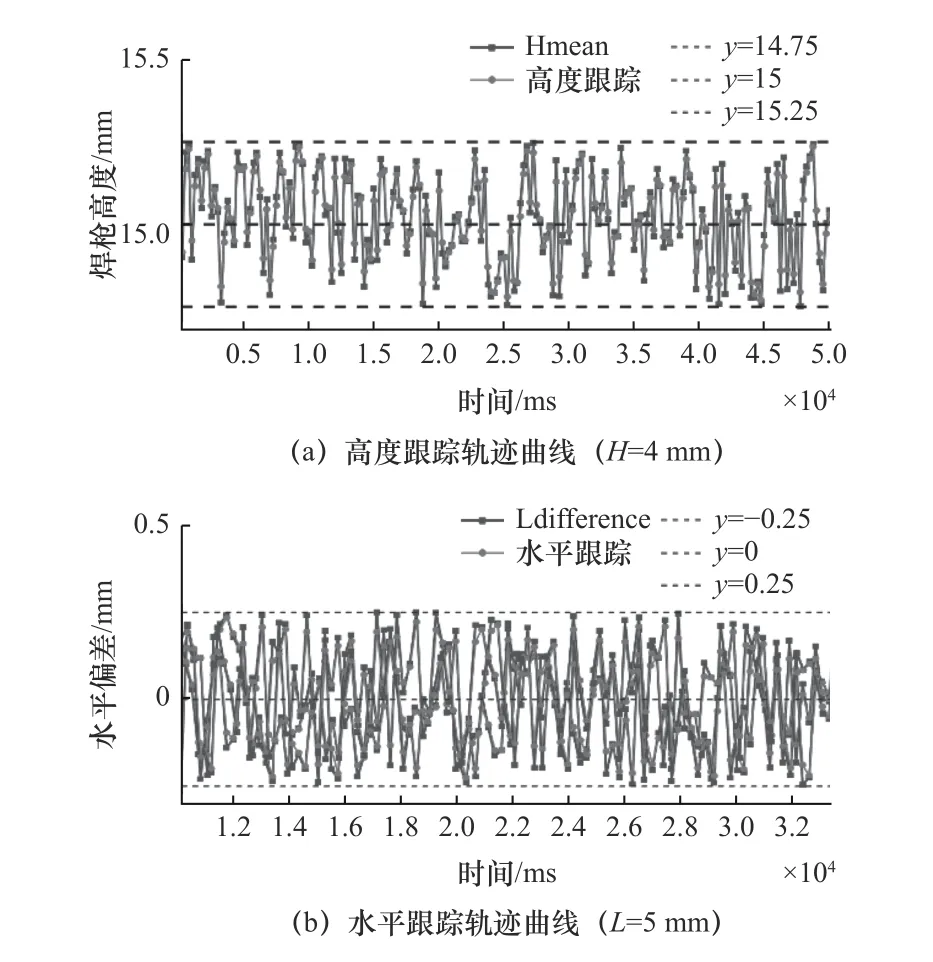
图19 整体跟踪轨迹曲线

通过以上三组实验可得出以下结论：计算得到的偏差符合偏差维持在0.5 mm 以内这一跟踪指标（图20），跟踪的精度均符合焊接工艺中所描述的自动焊接误差≤0.5 mm 这一精度要求[11]，并且焊缝成形良好，无明显凸起，能够满足实际焊接要求，说明焊枪的整体跟踪算法可行。

图20 试件一侧抬高4mm 和偏移5mm 焊缝图

4 结语

基于EKF 的GMAW 实时焊缝跟踪技术主要由GMAW 焊接设备、信息采集设备和控制设备组成。实验结果表明，该技术用于焊接设备对焊枪的跟踪是可行和稳定的。本研究的主要成果可概括如下：

（1）针对V 形坡口焊缝的焊接电流的特点，建立了高度和水平偏差提取数学模型，解决了焊枪摆动中心对准焊缝中心的问题。

（2）采用了EKF 算法解决了焊接过程中的非线性、噪声和干扰等问题，实现对焊枪的精确控制。

（3）焊枪焊缝实时跟踪的偏差成功控制在0.5 mm以内，满足了焊接质量和焊缝跟踪控制的要求。

为GMAW 实时焊缝跟踪技术的发展提供了重要依据。