基于动态启发的双向搜索A*路径规划算法

陈家伟 许颖婷 陈淑婧 张霖 蔡志明

DOI：10.19850/j.cnki.2096-4706.2024.02.019

收稿日期：2023-06-12

基金项目：福建工程学院校科研启动基金（GY-Z21064）

摘  要：针对传统路径规划A*算法搜索速度慢，且所得路径转角过大的问题，提出了一种基于双向搜索的A*路径规划算法。首先调整A*搜索算法的整体搜索方向为双向搜索，初步提升搜索速度；其次，在规划过程中引入动态权重系数来调节启发式函数，通过平衡路径长短与规划速度之间的关系，进一步提高搜索速度；最后采用B样条曲线对所规划的路径进行平滑优化，解决A*算法规划路径转角过多无法满足移动机器人实际运动控制的问题。仿真实验结果表明，相比传统的A*算法，该算法在搜索节点和规划时间方面分别平均减少79.24%和62.56%。

关键词：移动机器人；A*路径规划；双向搜索；动态权重系数；B样条曲线优化

中图分类号：TP242.6  文献标识码：A  文章编号：2096-4706（2024）02-0086-06

A Bidirectional Search A* Path Planning Algorithm Based on Dynamic Heuristic Method

CHEN Jiawei1， XU Yingting1， CHEN Shujing1， ZHANG Lin1， CAI Zhiming1，2

（1.School of Electronic， Electrical Engineering and Physics， Fujian University of Technology， Fuzhou  350118， China;

2.National Demonstration Center for Experimental Electronic Information and Electrical Technology Education， Fujian University of Technology， Fuzhou  350118， China）

Abstract： Aiming at the problem that the traditional path planning A* algorithm has slow search speed and the resulting path turning angle too large， an A* path planning algorithm based on bidirectional search is proposed. Firstly， the overall search direction of A* search algorithm is adjusted to bidirectional search to initially improve the search speed. Secondly， dynamic weight coefficients are introduced in the planning process to adjust the heuristic function to further improve the search speed by balancing the relationship between path length and planning speed. Finally， B-spline curve is used to smooth and optimize the planned paths to solve the problem that the A* algorithm planning paths with too many turning angles cannot meet the actual motion control. The results of simulation experiments show that compared with the traditional A* algorithm， the algorithm in this paper reduces the search nodes and planning time by 79.24% and 62.56%， respectively.

Keywords： mobile robot; A* path planning; bidirectional search; dynamic weight coefficient; B-spline curve optimization

0  引  言

自主移动机器人（Autonomous Mobile Robot， AMR）是近年来人工智能研究领域的一个热点研究方向。移动机器人路径规划是AMR的一种关键技术，它可以帮助机器人实现自主移动，其基本思想是通过分析机器人所处的环境，计算出最优的路径，使机器人能够安全、有效地抵达目标区域顺利完成任务[1]。

作为移动机器人研究的核心技术之一移动机器人路径规划得到了国内外学者的广泛关注和深入研究[2]。Peter等人结合了最佳优先搜索（Best First Search， BFS）算法和Dijkstra算法，提出了著名的A*算法[3]。但A*算法也存在一些不足：由于A*算法需要同时维护OPEN List和CLOSED List两个列表，并对每个展开的节点计算代价值，这往往会导致计算量大，内存占用严重且计算时间长的问题。针对上述缺点，赵晓等人使用跳点搜索的方式改进A*算法，省略了A*算法大量的不必要节点，从而减少了计算量[4]。Xiang等人提出了一种改进邻域搜索的A*算法，并将其与贪心算法结合，有效减少了路径长度[5]。为了减少搜索節点并提高实时性，杨光永等人提出了一种使用余弦方向因子改进启发式函数的A*搜索算法[6]。同样地，张阳伟等人提出了一种变步长双向搜索A*算法，减少A*算法搜索节点数[7]。

为了解决A*算法在路径规划过程中存在的路径搜索节点数量多、搜索时间长、最终路径总转角大的问题，本文引入动态权重系数改进启发式函数并结合双向搜索策略对A*算法加以改进。在改进的A*算法生成规划路径后使用B样条曲线对路径进行平滑处理，使其符合移动机器人运动学模型。

1  传统A*搜索算法

A*搜索算法是一种启发式的图搜索算法，它同时具有Dijkstra算法和BFS算法的特点，该算法既可以找到最短路径，又拥有比较较快的搜索速度。A*算法的代价函数如式（1）所示：

（1）

其中G（n）表示从起始节点到节点n的实际代价函数，H（n）表示从节点n到目标节点的启发式评估代价函数，F（n）表示节点n的总代价函数。启发式函数采用曼哈顿距离，其公式如式（2）所示：

（2）

在A*搜索算法中，搜索区域被转换成一个二维数组，栅格的中心被定义为节点n。数组的每个元素都是栅格地图的一个正方形。二维方格定义为可行区域（OPENLIST）或不可行区域（CLOSE LIST）。F（n）会评估OPEN LIST中的每个节点的代价值并确定节点的顺序。OPEN LIST用于记录已计算代价值但并未展开的节点，CLOSE LIST用于储存已展开的节点。

本文采用如图1所示的栅格地图（Grid Map）进行全局环境地图模型的构建，对环境中出现的障碍物以机器人尺寸半径向外膨胀一定距离作为栅格的尺寸进行栅格化，栅格化后不满一个栅格的障碍物区域也按照一个完整的栅格处理。

图中黑色栅格代表被障碍物所占据的区域，坐标（1，1）的栅格为设定的机器人运动起始点，坐标（14，14）的栅格为机器人任务目标终点，灰色栅格代表A*算法所遍历的节点。

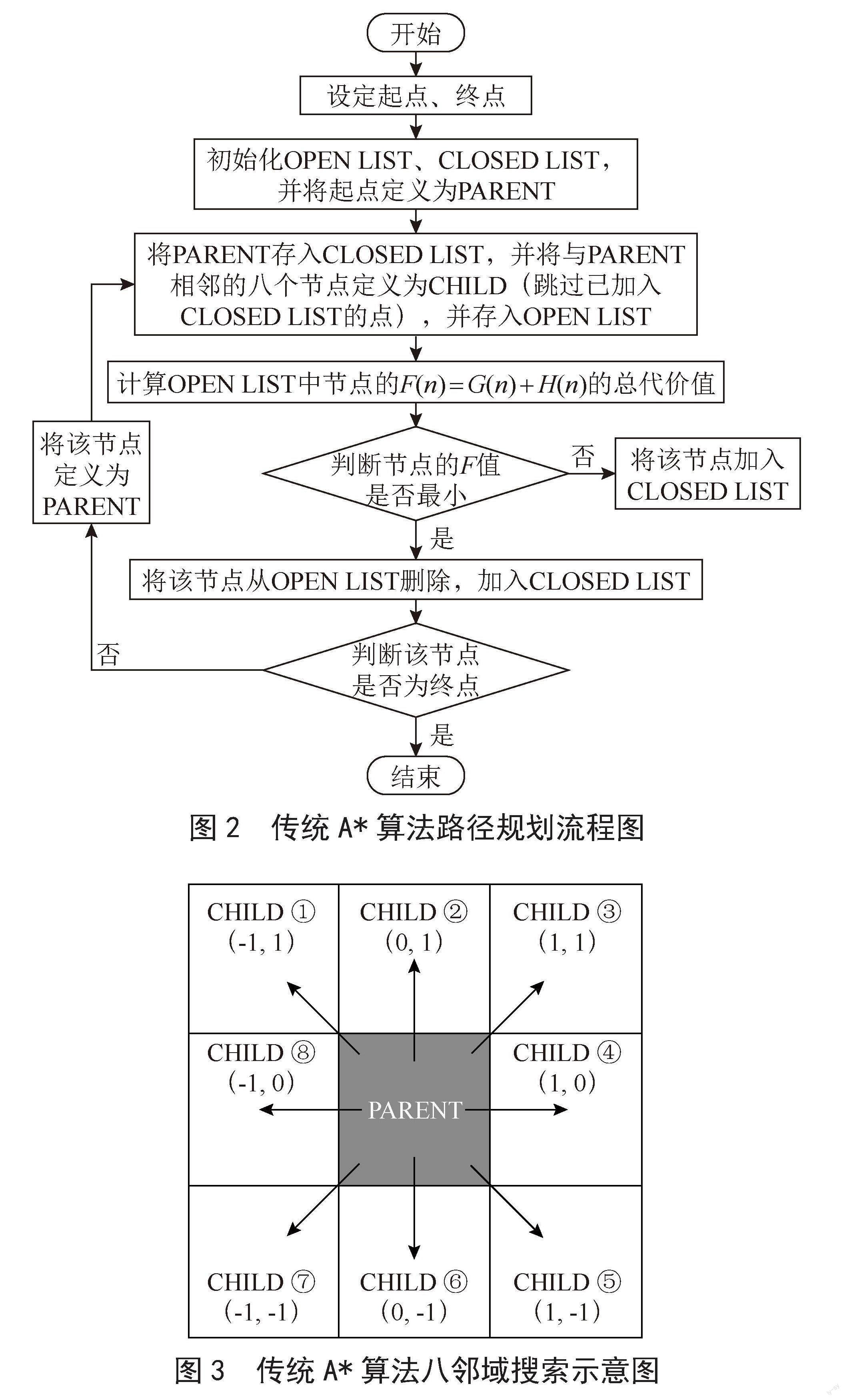
A*算法的工作流程如图2所示，通过循环判断待检测节点的总代价值来选择下一个节点。节点采用八邻域进行搜索，如图3所示，其中PARENT表示父节点即当前节点，CHILD表示父节点的子节点即当前节点的邻节点，图3中CHILD的坐标是PARENT的相对坐标值。

2  A*搜索算法的改进

2.1  双向搜索

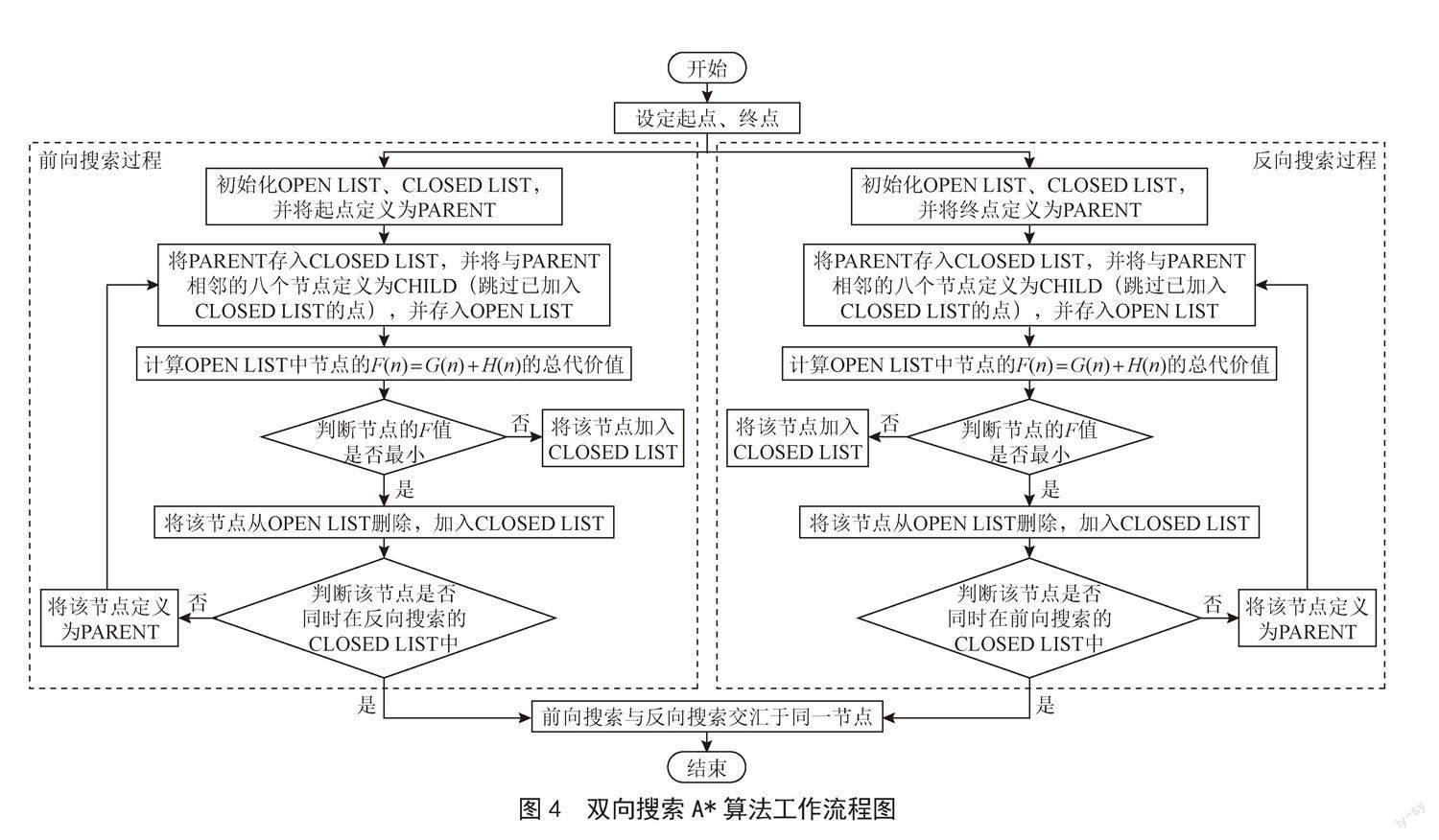
传统的A*算法搜索速度虽然相较于Dijkstra算法已有了较大的提升，但搜索速度仍然较慢，且搜索的节点偏多。因此，本文使用双向搜索的方式，提升A*算法的搜索速度，减少其遍历的节点数。双向搜索的方式会将起点和终点进行重映像：即起点与终点二者互为起点，也互为终点。双向搜索的过程主要分为前向搜索和反向搜索。在初始化OPEN List时，前向搜索过程将起点加入OPEN List并定义其为PARENT节点，而反向搜索过程是将终点加入OPEN List并定义其为PARENT节点。双向搜索A*算法实际流程如图4所示。当前向搜索过程与反向搜索过程交汇与同一节点时，算法结束，生成路径。

使用双向搜索A*算法进行路径规划的结果如图5所示。为了方便与传统A*算法的效果进行对比，图5使用了与图1相同的栅格地图、起点与终点。

图中黑色栅格代表被障碍物所占据的区域，坐标（1，1）的栅格为设定的机器人运动起始点，坐标（14，14）的栅格为机器人任务目标终点。

将图1与图5进行对比可以明显看出使用双向搜索A*算法所遍历的节点数要少于传统A*搜索算法。

2.2  动态启发

本文使用欧几里得距离作为启发式函数，一定程度上能够缩短规划算法得到的距离。欧几里得距离公式如式（3）所示：

（3）

由A*算法的总代价函数F（n）可知，当H（n） = 0时，A*算法会演变为Dijkstra算法。当H（n）≤G（n）时，A*算法所搜索的节点相较于Dijkstra算法会减少，搜索速度也会加快，且能找到一条最短路径。但此时所搜索的节点数仍比较庞大，搜索速度仍然不够快。当H（n）＞G（n）时，A*的搜索速度会比H（n）≤G（n）时更快，但可能无法找到一条最短路径。当H（n）?G（n）时，A*算法会演变为BFS算法。

在移动机器人的路径规划中往往期望总路径越短越好，且路径规划速度越快越好。因此，本文引入了动态权重系数w（n）来调整启发函数。由w（n）来控制H（n）与G（n）的比例关系，从而平衡路径长短与规划速度之间的关系。引入动态权重系数后，A*总代价函数如式（4）所示：

（4）

其中的动态权重系数w（n）定义如下式（5）所示：

（5）

式中的d（g）表示当前节点到目标点的欧几里得距离，d（s）表示起点到目标点的欧几里得距离。当d（g）/d（s）≥0.3时，即当前节点在远离目标节点的位置时，选用较高的权重，这样便会使最终的H（n）值大于G（n）。此时，路径搜索过程更加注重速度。而当d（g）/d（s）＜0.3时，选用1作为权重。此时，路径规划过程转换为传统A*的搜索过程，即搜索速度与路径长度兼顾的模式。

图6（a）是传统A*算法在64×64地图下的搜索结果，图6（b）是双向搜索A*算法在64×64地图下的搜索结果，图6（c）是添加动态权重系数后的双向搜索A*算法在64×64地图下的搜索结果。图7（a）是传统A*算法在128×128地图下的搜索结果，图7（b）是双向搜索A*算法在128×128地图下的搜索结果，图7（c）是添加动态权重系数后的双向搜索A*算法在128×128地图下的搜索结果。显然，添加权重系数后的双向搜索A*算法所遍历的节点数大幅下降。

2.3  基于B样条曲线的路径优化

A*算法搜索得到的路径存在转角过多，路线不够平滑的问题。针对A*路径转角过多过大的问题，Zhang等人提出了一种结合人工势场方法的启发式函数，提高了执行效率并减少了路径转折点数量[8]。Ou等人引入了一种基于几何特征去除冗余节点进行路径平滑的策略，该方法能夠有效地去除冗余节点保障移动机器人行驶安全[9]。刘钰铭等人提出了一种基于动态弦定弧过渡的路径平滑处理方法[10]。然而，更加主流的路径优化方法是贝塞尔曲线优化[11]。

贝塞尔曲线是适用二维图形的一种数学曲线，一般是用于一些矢量图的设计。不过在路径规划中，依然可以使用贝塞尔曲线来优化路径，使其更加平滑[12-14]。二阶贝塞尔曲线原理示意图如图8所示。

贝塞尔曲线由起点、终点和控制点组成，根据控制点的个数和位置决定了这个曲线的最终样式。在图8中，P1、P2、P3为控制点，在线段P1P2中，任意选取一点 ，计算比例 ，根据计算得到的比例在线段P2P3上选取点 ，使得 ，连接 。在线段  上选取点 ，使得 ，此时的点 即是二阶贝塞尔曲线上的点。遍历线段P1P2与线段P2P3上所有的点后，将得到的所有的点  连接起来便可以得到二阶贝塞尔曲线，如图8中曲线所示。

但是贝塞尔曲线同样存在许多缺陷：1）一旦确定了控制点个数，也就确定了贝塞尔曲线的阶数。2）贝塞尔曲线的拼接过程比较复杂。3）贝塞尔曲线不能做局部的修改。

基于上述条件，本文采用B样条曲线（B-spline curve）进行路径优化。B样条曲线本质上是一个分段连续多项式。整条曲线是一个完整的表达式，但是其内在的量是分段的，如，某条B样条曲线是由若干三阶曲线拼接而成，但两两之间又满足二次连续的关系[15]。这样既克服了波动现象，得到的曲线又是低次的，有统一表达式的。

对于n+1个控制点Pi（i = 0，1，2，…，n）和一个节点向量U = {u0，u1，u2，…，um}，依次连接这些控制点可以组成一个特征多边形。此时K + 1阶（K次）B样条曲线的一般表达式如下式（6）所示：

（6）

其中Ni，k （u）是K次B样条基函数，其递归公式如式（7）所示：

（7）

低阶的B样条曲线平滑度较差，但B样条曲线的阶数越高，其计算复杂度也将随之升高。高阶的曲线优化后的路径还可能穿越障碍物区域[16]。经实验，本文使用十階B样条曲线对算法得到的路径进行优化，并将其与使用连续二阶贝塞尔曲线优化的路径进行对比，得到如图9所示结果。图9（a）是64×64分辨率地图下连续二阶贝塞尔曲线路径优化结果图，其中折线是路径规划所得路径，曲线是二阶贝塞尔曲线优化后的路径。图9（b）是64×64分辨率地图下十阶B样条曲线路径优化结果图，其中折线是路径规划所得路径，曲线是十阶B样条曲线优化后的路径。通过对比，可以很明显地看出十阶B样条曲线的路径更加平缓，更符合机器人实际的运动学模型。

3  实验结果与分析

本文所使用的硬件环境为：Intel（R） Core（TM） i7-10870H CPU @ 2.20 GHz；操作系统为Windows 10 22H2；软件环境为：PyCharm 2021.2.3（Community Edition）；所使用的编程语言为：Python 3.9。

为验证本文所提出的基于动态启发双向搜索的A*路径规划算法的有效性，本文设计了16×16、64×64、128×128三种分辨率的栅格地图作为机器人环境模型的仿真，在给定同一起点和目标点的情况下，重复10次实验，并对实验数据进行求平均处理后得到如表1、表2、表3所示实验数据。

与传统A*算法和未经改进的双向搜索A*算法相比，本文所提出的采用动态启发双向搜索A*算法在三种不同分辨率地图下的性能均有所提升，搜索节点个数减少了58.93%～91.50%，规划时间减少了34.19%～80.89%。如本文2.2节内容所述，在分辨率较大的128×128地图环境下，本文改进的动态启发双向搜索A*算法由于在搜索初期启发函数的权重较大，无法保证路径长度的最短。

4  结  论

本文针对自主移动机器人使用A*算法搜索路径时存在的搜索速度慢，生成的路径转角过多，安全阈值低的问题，提出了一种基于动态权重优化和B样条曲线优化的双向搜索A*算法。通过引入动态权重系数，修改启发函数值来达到提高路径规划速度的目的。同时，使用B样条曲线对路径进行平滑优化，使其更符合机器人运动学模型。实验证明，本文所提出的改进算法大幅减少了路径规划时间和路径转角，更加符合自主移动机器人的运动学模型，具有较好的实用性。但本文算法在较大分辨率的地图场景中无法保证路径的最优，动态启发函数还有改进空间。进一步优化算法后，有望在找到最短路径的情况下，大幅改善路径规划速度，更适合机器人的实际应用。

参考文献：

[1] 林韩熙，向丹，欧阳剑，等.移动机器人路径规划算法的研究综述 [J].计算机工程与应用，2021，57（18）：38-48.

[2] 李晓旭，马兴录，王先鹏.移动机器人路径规划算法综述 [J].计算机测量与控制，2022，30（7）：9-19.

[3] PETER H，N NILS，R BERTRAM. A Formal Basis for the Heuristic Determination of Minimum Cost Paths [J].IEEE Transactions on Systems Science and Cybernetics，1968，4（2）：100-107.

[4] 赵晓，王铮，黄程侃，等.基于改进A*算法的移动机器人路径规划 [J].机器人，2018，40（6）：903-910.

[5] XIANG D，H LIN，J OUYANG，et al. Combined improved A* and greedy algorithm for path planning of multi-objective mobile robot [J/OL].Scientific Reports，2022，12（1）：13273（2023-08-02）.https：//link.springer.com/article/10.1038/s41598-022-17684-0.

[6] 杨光永，戈一航，晏婷，等.基于调和A*算法在移动机器人中的研究 [J].现代电子技术，2022，45（4）：171-176.

[7] 张阳伟，乔越，李成凤.基于四叉树栅格环境的变步长双向A*算法 [J].控制工程，2021，28（10）：1960-1966.

[8] ZHANG J，WU J，SHEN X，et al. Autonomous land vehicle path planning algorithm based on improved heuristic function of A-Star [J/OL].International Journal of Advanced Robotic Systems，2021，18（5）：（2021-09-14）.https：//doi.org/10.1177/17298814211042730.

[9] OU Y，Y FAN，X ZHANG，et al. Improved A* Path Planning Method Based on the Grid Map [J/OL].Sensors （Basel），2022，22（16）：6198（2022-08-18）.https：//doi.org/10.3390/s22166198.

[10] 刘钰铭，黄海松，范青松，等.基于改进A*_DWA算法的移动机器人路径规划 [J/OL].计算机集成制造系统：1-20（2022-11-28）.http：//kns.cnki.net/kcms/detail/11.5946.TP.20221125.1957.004.html.

[11] 岳高峰，张萌，沈超，等.移动机器人导航规划的双向平滑A-star算法 [J].中国科学：技术科学，2021，51（4）：459-468.

[12] 谢春丽，高胜寒，孙学志.融合改进A*算法和贝塞尔曲线优化的路径规划算法 [J].重庆理工大学学报：自然科学，2022，36（7）：177-187.

[13] 李二超，齐款款.贝塞尔曲线融合双向蚁群算法的移动机器人路径规划 [J].陕西师范大学学报：自然科学版，2022，50（3）：79-88.

[14] 方文凯，廖志高.基于改進A*算法的移动机器人全局路径优化研究 [J].广西科技大学学报，2023，34（1）：73-78+84.

[15] 朱平，汪国昭. 变次数B-样条曲线 [J].浙江大学学报：工学版，2009，43（5）：789-795.

[16] 张跃明，薛奇，纪姝婷.满足曲率约束的B样条曲线连续路径平滑方法 [J].华中科技大学学报：自然科学版，2022，50（5）：59-65+72.

作者简介：陈家伟（1997—），男，汉族，浙江宁波人，硕士研究生在读，研究方向：室内移动机器人定位与导航；许颖婷（2000—），女，汉族，福建漳州人，硕士研究生在读，研究方向：室内移动机器人定位与导航；陈淑婧（1998—），女，汉族，福建漳州人，硕士研究生在读，研究方向：室内移动机器人定位与导航；张霖（1979—），男，汉族，福建泉州人，讲师，博士，研究方向：模拟/混合信号IC设计、机器识别；通讯作者：蔡志明（1977—），男，汉族，福建漳州人，教授，博士，研究方向：室内移动机器人定位与导航。