集成学习框架下的车辆跟驰行为建模

李 立,李仕琪,徐志刚,李光泽,汪贵平

(1.长安大学 电子与控制工程学院,西安 710064; 2.长安大学 信息工程学院,西安 710064)

车辆跟驰模型描述了单车道上相邻两车之间的运动关系,是微观交通流仿真、道路通行能力分析、自动驾驶算法等方面研究的基础模型之一,在交通工程学理论体系中占据重要地位[1]。现有跟驰模型可以分为理论驱动模型和数据驱动模型两大类[2]。理论驱动模型采用严格的数学表达式描述跟驰车辆的动力学机制,具有精确的物理意义,能够确保在合理的参数设定下具有明确稳定的输出,代表模型包括GM(general motor)模型、Gipps模型和IDM(intelligent driver model)模型。实际交通流中,车辆跟驰行为受驾驶风格、交通环境、车辆类型等因素的影响呈现一定的随机性和非线性。理论驱动模型结构相对简单,模型参数较少,使其难以描述实际复杂交通流中的车辆跟驰行为,从而导致对跟驰行为的预测失准或仿真失真。针对这种情况,一种常见的解决方法是采用不同交通流状态下的实测数据标定跟驰模型,并为其设置分类应用条件,但是交通流状态划分方法、跟驰模型参数标定方法、预测结果评价指标等因素均可能影响跟驰模型的应用效果,提高模型应用的复杂度。

与理论驱动跟驰模型相比,近年来有较多研究采用数据驱动的方法构建跟驰模型。数据驱动跟驰模型利用数据科学与机器学习等理论和方法,从真实车辆行驶数据中挖掘跟驰行为特征,利用模型参数多、非线性规律拟合能力强的特点,学习数据中存在的复杂行为规律,使其经常获得比理论驱动模型更好的跟驰行为预测效果。文献[2]从模糊逻辑、人工神经网络、实例学习、支持向量回归、深度学习等5个方面对数据驱动跟驰模型的研究进行了综述。文献[3]将数据驱动跟驰模型分为基于神经网络、支持向量回归和K近邻等传统机器学习方法的模型和基于深度学习的模型。但是,数据驱动跟驰模型的参数连接关系缺乏明确的交通物理含义,且难以判断模型输入是否超出了安全驾驶阈值,这些缺陷可能影响模型预测结果可靠性并危及行车安全。通过近年来多次出现自动驾驶车辆安全事故[4-5],也说明单纯依靠数据驱动方式进行车辆跟驰行为建模和应用存在潜在安全风险。

为了综合利用上述两类跟驰模型的优点,有学者提出了理论与数据混合驱动的跟驰模型。文献[6]采用线性函数融合了理论驱动与数据驱动跟驰模型,发现融合模型比非融合模型具有更高的跟驰行为预测精度。文献[7]采用自适应卡尔曼滤波方法组合了多种跟驰模型,找到了预测精度高的融合跟驰模型。文献[8]利用最优加权组合理论,建立IDM模型与径向基函数神经网络融合的跟驰模型。然而,现有理论与数据混合驱动跟驰模型所采用的融合方法通常直接对两类模型的输出进行线性加和,并未对两类模型的参数和权重进行深度融合,导致两类模型的优势未得到充分的发挥和利用。

除了与理论驱动跟驰模型融合之外,另一种提升数据驱动跟驰模型表现的途径在于合理增加模型变量。微观驾驶行为可能受到周边车辆行为、道路设施条件、车内外交通信息等因素的影响[2],然而现有多数数据驱动跟驰模型中纳入的变量与理论驱动跟驰模型类似,这可能导致模型欠拟合,因此有必要进一步从车辆轨迹数据中提取更多能够反映真实驾驶过程中驾驶人观察信息的变量,并将其引入数据驱动跟驰模型中[3]。

综上,本文提出了一种基于集成学习框架的理论和数据驱动跟驰模型融合方法。利用集成学习框架可以综合应用多种同质或异质基学习器的优势,通过构建多级学习器对理论和数据驱动跟驰模型进行组合、训练和应用,提高模型的预测精度和泛化能力。同时将跟驰车辆所在队列状态及其周边行驶条件因素引入数据驱动跟驰模型中,以进一步提升模型学习复杂交通条件下车辆跟驰行为的能力。使用真实车辆轨迹数据集对所构建模型进行训练和测试,来验证所提出方法的有效性。本文为复杂交通流条件下的车辆跟驰行为建模提供了新的思路,研究成果有助于提升跟驰行为预测和微观交通仿真精度。

1 数据与变量

1.1 数据

本文使用highD自然驾驶轨迹数据集[9]作为基础数据。此数据集由无人机在德国高速公路6个路段上空拍摄的十余个小时的视频中提取的车辆轨迹数据组成,数据字段包括车辆经纬度、所在车道、行驶方向、外形尺寸、类型、速度、加速度、周边车辆编号等。数据采集地点为平直路段,上下游匝道距离较远,因此车辆换道现象较少,多数车辆处于跟驰或自由行驶状态。本文使用IDM模型作为理论驱动跟驰模型的代表,此模型具有明确的物理意义且参数相对较少,广泛用于多种交通状态下的跟驰行为建模,以及网联自动驾驶控制算法中,具有较强的适用性及可拓展性。IDM模型变量包括跟驰车速度、与前导车的间距以及与前导车的速度差等,这些变量值可从数据集中直接计算获得,同时模型参数将参考数据集中特定字段的统计值设定。数据驱动模型中除了纳入上述变量外,其他纳入变量的计算相对复杂,详述如下。

1.2 车辆队列

在车流密度较高的条件下,同一车道上密集接续行驶的多辆车在运动方式上经常表现出一定的相似性,会从客观上形成车辆队列,如图1所示。过往有学者[10-11]将跟驰车辆前后多车的运动状态变量纳入跟驰模型中。实际上,跟驰驾驶员通常难以直接准确观察和衡量前后多车运动参数,更合理的行为模式是跟驰驾驶员根据非直接相邻的前后车辆运动状态估计其所在队列整体运动状态,并基于此调整驾驶行为。因此,本文将跟驰车辆所在队列的平均运动状态纳入数据驱动跟驰模型中。本文通过设置车辆跟驰状态判断条件划分车辆队列。筛选highD数据集中换道数为0、有效跟驰时长16 s以上、处于稳定跟驰状态即跟驰车辆速度与所在车队的平均速度平均差值不超过2 m/s的车辆轨迹,然后根据数据字段中的跟驰车辆编号确定其是否归入车辆队列。一共得到1 241个车辆队列,共7 306条车辆轨迹,所有车队中车辆的平均间距和平均车速分别为34.304 m和21.479 m/s,平均车头时距为1.6 s,最大加速度为5.02 m/s2,最大减速度为-4.46 m/s2。描述车辆队列平均运动状态的变量包括车辆队列中的平均间距、平均车头时距和平均碰撞时间(time to collision)。设定t时刻第i个队列平均运动状态变量Pi(t)为

(1)

图1 车辆队列及相关变量

1.3 周边行驶条件

除了本车道前后车辆的影响外,过往实证和仿真研究[12-13]均发现跟驰车辆相邻车道的临近车辆也可能影响跟驰车辆的驾驶行为,影响因素包括车辆侧向间距、驾驶员换道超车意图等。为了描述车辆队列中跟驰车辆的周边行驶条件,定义t时刻队列i内部第j辆跟驰车周围行驶条件的变量Fi,j(t)表达式为

(2)

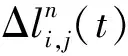
图2 周边车辆及相关变量

2 集成学习框架下的跟驰行为建模

2.1 stacking集成学习方法

集成学习是一种通过构建和结合多个学习器,降低单一学习器灵敏度不同带来的误差,提高模型泛化能力、鲁棒性和预测精度的机器学习方法。常见的集成学习方法包括自助聚合(bagging)法、提升(boosting)法、堆叠(stacking)法。由于bagging法和boosting法主要用于同质学习器的集成,而理论和数据驱动跟驰模型的建模机制区别明显,因此本文引入面向异质学习器的stacking法,将跟驰行为建模划分成两个阶段,针对不同阶段的建模需求分别构建一级学习器和二级学习器,对理论和数据驱动跟驰模型进行集成与融合。首先,将数据集划分成3个子集,分别是训练集、验证集和测试集。接着,将理论驱动模型和数据驱动模型作为两个一级学习算法,使用训练集对其进行训练,即标定理论驱动模型的参数和训练数据驱动模型的网络权重,构成一级学习器。然后,使用验证集作为一级学习器的输入,将获得的输出与验证集中的数据标签组合,生成一个新的数据集。接着,使用新数据集训练二级学习算法,获得二级学习器的网络权重和模型参数。最后,将测试集作为训练后的一级和二级学习器的输入,对比测试集成跟驰模型的预测效果。此方法的伪代码如下所示。流程如图3所示。

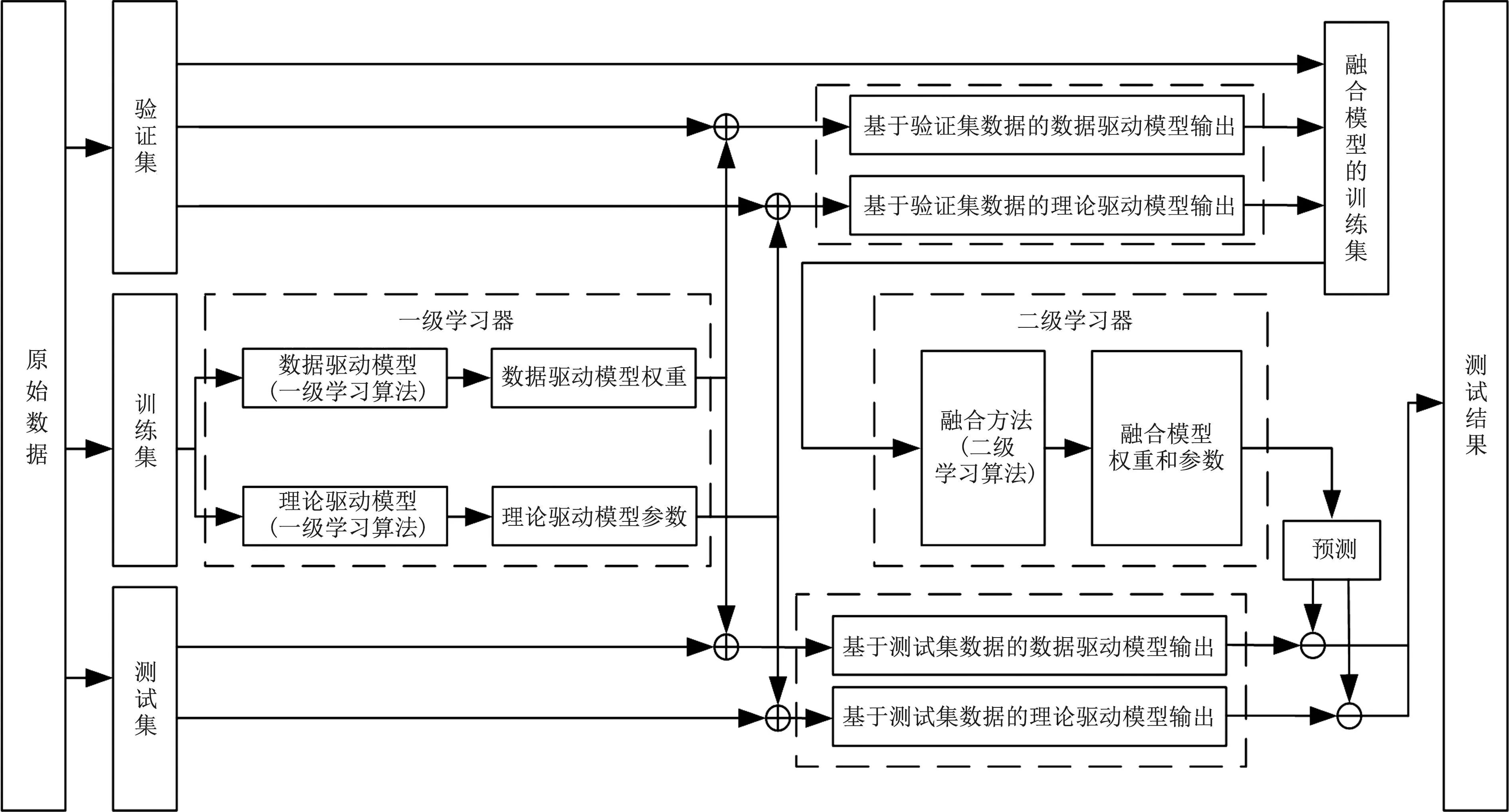
图3 集成学习框架下的跟驰行为建模方法

定义:数据集Dr={(xr,m,yr,m)}(r=1～3),其中D1、D2和D3分别为训练集、验证集和测试集,样本编号m=1～Mr,其中M1、M2和M3分别为子集D1、D2和D3的样本数量,xr,m和yr,m分别为不同子集中样本的数值与标签;新的训练集D′2=∅;一级学习算法ζ1、ζ2,一级学习器θ1、θ2;二级学习算法μ,二级学习器β。

步骤:

forq=1,2 do:

训练θq:θq=ζq(D1)

end for

form=1,…,M2do:

forq=1,2 do:

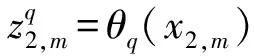
end for

end for

训练β:β=μ(D′2)

输出:集成模型H(x3m):H(x3m)=β(θ1(x3,m),θ2(x3,m))

其中,一级学习算法的设置详见2.2节和2.3节。为了对一级学习器的输出特征进行再学习,在二级学习算法中可以采用线性或非线性方法对一级学习器的输出进行再学习。本文选择了表1所示的11种线性和非线性方法作为二级学习算法,将通过对比测试选择性能最佳的二级学习算法。

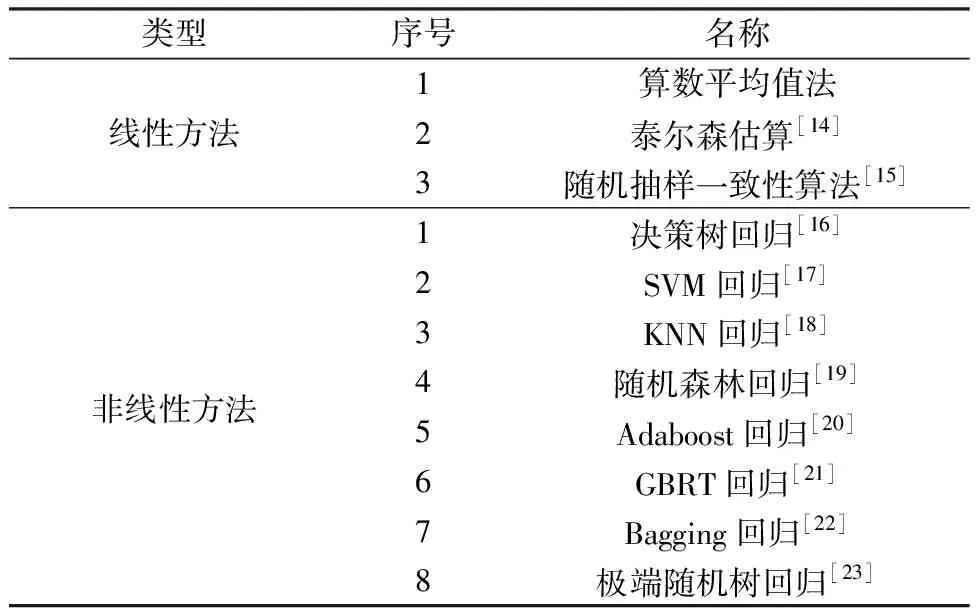
表1 二级学习算法分类

2.2 理论驱动跟驰模型

本文选择IDM模型作为stacking集成学习框架下的一级学习算法之一。IDM模型描述了跟驰车的加速度与速度、与前导车的间距以及速度差的关系。将IDM模型应用于本文研究场景中,可得t时刻队列i内部第j辆跟驰车的加速度为

(3)

式(3)的前半部分为第j辆跟驰车的自由加速度,其与最大加速度amax、期望速度ve以及t时刻车速vi,j(t)有关,其中δ为加速度指数。式(3)的后半部分为跟驰车的减速策略,当跟驰车与前导车间距过小时,该策略被触发,其中di,j,j-1(t)为t时刻第j辆跟驰车与其前导车之间的距离,d*(t)为t时刻的期望最小间距,可表示为

(4)

式中:hσ为安全车头时距,dmin为拥堵间距,b为驾驶员期望减速度,Δvi,j,j-1(t)为t时刻第j辆跟驰车与其前导车之间的速度差。参考1.2节所述所纳入车辆运动状态信息。其中,amax为5 m/s2,ve为30 m/s,δ为4,hσ为1.5 s,dmin为2 m,b为4.5 m/s2。

2.3 数据驱动跟驰模型

由于跟驰驾驶员往往依赖历史驾驶行为和过去一段时间内的交通状态进行行驶决策,即其决策行为存在记忆效应,因此本文选择长短时记忆(long-short term memory,LSTM)网络[24]和门控循环单元(gate recurrent unit,GRU)网络[25]对跟驰行为进行建模,并将其作为stacking集成学习框架下的另一种一级学习算法。LSTM网络在其单元之间传递信息时,分别使用单元状态和隐藏状态存储长期记忆和短期记忆。GRU网络可看作是LSTM网络的一种变体,其结构比LSTM网络简单,不包含单元状态,使用隐藏状态传递信息。图4所示为数据驱动跟驰模型的结构。模型训练中采用均方误差(mean-square error,MSE)作为回归损失函数,Sigmoid作为激活函数,Adam作为优化算法。

图4 数据驱动跟驰模型的结构

定义t时刻影响第i个车辆队列中第j辆跟驰车辆行为的因素组合Wi,j(t)为

Wi,j(t)=[Pi(t),Fi,j(t),Gi,j-1,j(t)]

(5)

式中:Pi(t)为车辆队列影响因素(见式(1)),Fi,j(t)为周围驾驶环境影响因素(见式(2)),Gi,j-1,j(t)为第j辆车跟驰车与其前导车之间的时空关系,定义为

Gi,j-1,j(t)=[di,j-1,j(t),Δvi,j-1,j(t),vi,j(t),ai,j(t)]

(6)

Wi,j(t-NT)]

(7)

式中:N为所分析历史时段内时间节点数量,T为此时段内相邻时间节点的间隔,s为此时段内第s个历史时刻。

2.4 评价指标

使用3种评价指标测试所构建跟驰模型的性能,分别是对称平均绝对百分比误差(symmetric mean absolute percentage error,SMAPE)、平均绝对误差(mean absolute error,MAE)和平均绝对相对误差(mean absolute relative error,MARE),这些指标常用与评价跟驰模型对实际车辆轨迹的预测精度[3,6,26],分别为

(8)

(9)

(10)

3 计算结果与分析

3.1 一级学习器

通过两组试验确定作为一级学习器的数据驱动跟驰模型的网络结构和训练过程的学习率,并采用一组试验对比理论驱动模型和数据驱动模型的性能。

1)网络结构。LSTM网络和GRU网络包含有输入层、隐藏层和输出层,其中输入层和输出层的维数分别根据跟驰模型中所纳入的影响因素数量和模型输出的预测值数量确定。本文为这两种网络设置了单一隐藏层,以避免传统递归式结构网络可能发生的梯度弥散问题。表2报告了采用不同隐藏层神经元数量的数据驱动跟驰模型性能,可以发现,采用结构1、2、3的模型隐藏层神经元个数过少,导致学习效果不如采用结构4、5的模型。由于增加隐藏层神经元个数会延长模型解算时间,综合对比采用结构4、5、6的模型性能,最终选定结构5为最优模型结构。

表2 不同结构数据驱动模型性能

2)学习率。学习率是训练数据驱动模型的重要参数。表3中报告了不同学习率下具有最优结构的模型的性能。可以发现,由于学习率过高使得算法很难收敛到最低点,采用学习率1、2的模型误差较大。与之相比,采用学习率3、4的模型误差明显降低。由于采用学习率4的模型训练时间较久,且学习效果与采用学习率3的模型接近,因此选择学习率3为最优学习率。

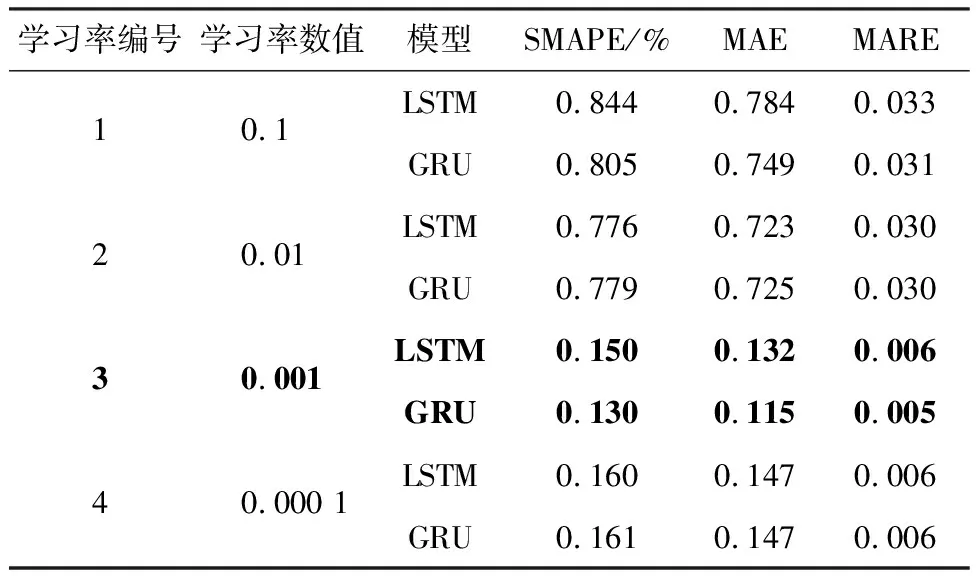
表3 不同学习率下数据驱动模型性能

3)对比模型。上述试验结果表明,使用网络结构5且设置学习率为0.001时,数据驱动模型能够获得最佳跟驰行为预测精度。采用相同的数据对IDM模型进行标定和测试,发现IDM模型的跟驰行为预测精度为SMAPE=0.740%,MAE=0.427,MARE=0.020。对比二者模型性能可以发现,具有最优网络结构和学习率的数据驱动跟驰模型的预测精度优于IDM模型。

3.2 融合模型

对于在stacking集成学习框架下获得的两个融合跟驰模型IDM-LSTM-stacking和IDM-GRU-stacking,表4给出了采用均值法、泰尔森估算和随机采样一致性线性回归3种线性二级学习算法后的模型预测结果。为了便于对比,表中同时给出了单独使用IDM模型和数据驱动模型的预测结果。可以发现,IDM模型的预测误差大于GRU和LSTM模型的预测误差,而IDM-LSTM-stacking和IDM-GRU-stacking模型的误差在理论驱动模型和数据驱动模型之间。这说明采用表中3种线性二级学习算法的模型并未能很好地对一级学习器的输出特征进行再学习,而其效果类似于对理论和数据驱动模型的输出进行了折中。

表4 3类跟驰模型性能

表5中给出了采用表1中8种非线性方法作为二级学习算法的融合跟驰模型的预测精度。对比表4中的结果可以发现,对于同样的输入数据,采用非线性二级学习算法的模型预测精度明显比IDM模型和采用线性二级学习算法的模型更高,也高于单纯的数据驱动模型。对于IDM-LSTM-stacking模型来说,采用非线性方法6即GBRT回归法的模型预测精度最高;对于IDM-GRU-stacking模型来说,采用非线性方法4即随机森林回归法的模型预测精度最高。上述结果说明,两种一级学习器即理论驱动跟驰模型和数据驱动跟驰模型的输出特征存在着复杂的非线性关系,需要采用非线性二级学习算法才能更好地对它们的输出特征进行再学习。

表5 采用非线性二级学习算法的跟驰模型性能

图5对比了IDM模型、GRU模型、LSTM模型、采用随机森林回归方法的IDM-GRU-stacking模型和采用GBRT回归方法的IDM-LSTM-stacking模型预测的车辆轨迹和真实车辆的轨迹。可以发现,采用随机森林回归方法的IDM-GRU-stacking模型和采用GBRT回归方法的IDM-LSTM-stacking模型比IDM模型、GRU模型和LSTM模型的轨迹预测精度高。

为了对比验证所构建集成学习跟驰模型稳定性及其对宏观交通流状态的影响,设计了如下数值模拟实验。假定由100辆跟驰车组成的车队在长度为2 000 m的三车道环路的中间车道上行驶,三车道环路的左右两侧车道交通流随机生成。跟驰车队的初始状态为稳定均衡状态,即车辆等间距分布,任意两车初始车头间距为20 m,所有车辆的车身长度为5 m,初始速度21.466 m/s,初始加速度为0 m/s2,其他仿真条件参考文中理论和数据驱动跟驰模型设置。实验中,在t=300 s时向第一辆车施加扰动,令该车速度降为初始速度的一半即10.733 m/s,同时位置向前移动14 m。

图6为数值模拟实验结果,图中第一列为各模型输出的车队行驶轨迹,此列各子图中竖线标记出扰动的施加时刻,第二列为各模型输出的车速变化热力图。从图6中可以看出,施加扰动后GRU模型输出的跟驰车队行驶轨迹出现了明显紊乱,每辆车的速度随时间变化出现了显著波动,说明此跟驰模型的稳定性不佳;与GRU模型相比,IDM模型和LSTM模型输出的速度值虽然存在周期性波动,但是各车速度变化幅度相对较小,说明其稳定性优于GRU模型;与上述3个模型相比,施加扰动后IDM-LSTM-stacking模型和IDM-GRU-stacking输出的跟驰车队行驶轨迹更为平滑,且每辆车的速度并未呈现出周期性波动,其中IDM-GRU-stacking模型输出的各车速度虽然在个别时间点上会发生较大变化,但是速度波动能够很快平抑,而IDM-LSTM-stacking模型输出的速度波动随着时间变化逐步消失,车队恢复到稳定跟驰状态,即车队内车辆速度与车队平均速度的平均差值维持在0.6 m/s以内。

图6 环路仿真实验结果

4 结 论

1)为了提高考虑车辆队列和周边车辆干扰条件下车辆跟驰行为预测精度,提出了一种stacking集成学习框架下的跟驰模型融合方法,将代表理论驱动的IDM跟驰模型和数据驱动的LSTM和GRU跟驰模型作为一级学习算法,再使用特定的二级学习算法对一级学习器的输出特征进行再学习,构建出融合跟驰模型IDM-LSTM-stacking模型和IDM-GRU-stacking模型。

2)基于实测数据的模型性能测试结果表明,考虑了车辆队列和周围驾驶条件因素的LSTM和GRU跟驰模型比IDM模型的预测精度高;采用非线性二级学习算法的融合跟驰模型的预测精度高于采用线性二级学习算法的融合模型以及数据驱动模型。其中,采用GBRT回归的IDM-LSTM-stacking模型和采用随机森林回归的IDM-GRU-stacking模型能够获得最高的预测精度。基于数值仿真的模型稳定性测试结果表明,施加扰动后IDM模型和LSTM模型的稳定性优于GRU模型,IDM-LSTM-stacking模型和IDM-GRU-stacking模型的稳定性优于IDM模型、LSTM模型和GRU模型。

3)除了本文所考虑的因素以外,车辆跟驰行为还可能受到包括驾驶员心理在内的其他因素的影响,后续研究中可进一步将其纳入跟驰模型中,另外本文所提出的集成学习方法也可应用于其他微观驾驶行为建模中,以提高复杂交通条件下的车辆轨迹预测精度和微观交通流仿真精度。