基于遗传算法的智能变电站避峰负荷优化调控系统

吴雪，肖莹，张旺，诸德律，卢璐

（国网江苏省电力有限公司经济技术研究院，江苏南京 210008）

负荷调控是电力需求的一种体现，也是一种重要发展形式，其重点强调了分散负荷在激励信号影响下，使得电力消纳方式得到了有效改变，并以等效发电形式参与智能变电站调控，为系统削峰填谷提供重要支持。目前，智能变电站负载控制主要按照发电量来完成。当用户超过计划用电时，调度人员会告知用户通过减负荷、切断用户电源等方法进行控制，而不能控制分支用户。对于分支用户，必须派人员到现场强制停电,不但造成电力系统效率低，也严重影响了电力系统的运行状态。因此，有必要建立一套能够实时调控负荷的系统。

文献[1]提出了结合动态负载安全裕度评价指标的调控方法，在制定负荷温度约束条件的情况下，建立了电力系统的动态载流量计算模型，并对其进行动态分析。充分考虑站间转供，使用最大电流方法确定变电站各个母线段负荷点的供电能力，求出负荷安全裕度下的超额负荷量；文献[2]提出了基于环电流约束的负荷调控方法，该方法充分发挥了智能变电所的分布式电源调节潜能，并分析含DG 配电馈线的调节条件，得到配电馈线的合环稳定约束。通过对变电所电力均衡约束的分析，提出了一种以最少的电力输出为目标的调节模式。但是上述两种方法难以克服维数灾难。为了解决这一问题，提出基于遗传算法的智能变电站避峰负荷优化调控系统。

1 基于遗传算法的优化调控原理

为了解决智能变电站避峰负荷调控求解陷入局部最优解的问题，利用遗传算法调节网络参数。设计基于遗传算法的优化调控系统网络结构，如图1所示。

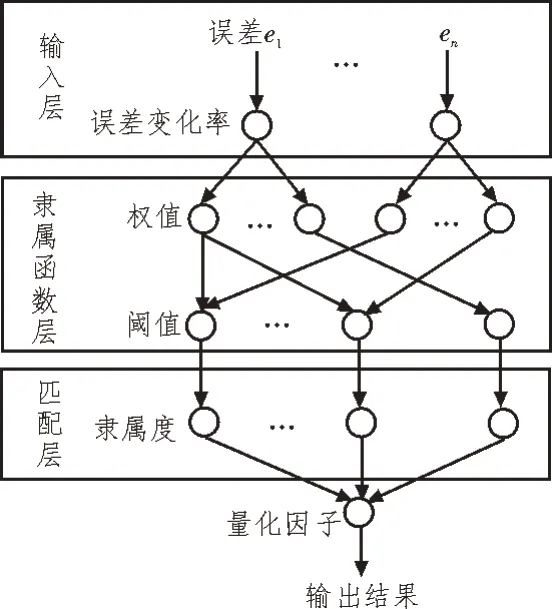
图1 基于遗传算法优化调控系统网络结构

由图1 可知，该网络结构主要是由输入层、隶属函数层和匹配层组成的。每层都具有明确的逻辑意义，其中第一层的关键节点分别是误差和误差变化率；第二层的关键节点分别是权值和阈值。利用高斯激励函数归一化处理[3-4]模糊变量，对该层的进行加权和阈值调节，调整高斯函数矢量，构建隶属函数，该层的输出为模糊变量从属程度；第三层的关键节点是隶属度，通过将不同隶属度相乘，能够获取模糊规则强度[5-6]。由于受控对象特点比较复杂，单靠一个量化因素难以达到理想控制效果。在此基础上，提出了一种基于归一化模糊定量分析方法，将控制系统输入变量从基础论域转换为模糊论域[7]。

2 系统硬件结构设计

基于遗传算法的优化调控原理，利用智能变电站现有的网络资源，搭建系统硬件结构，以满足避峰负荷优化调控需求，如图2 所示。

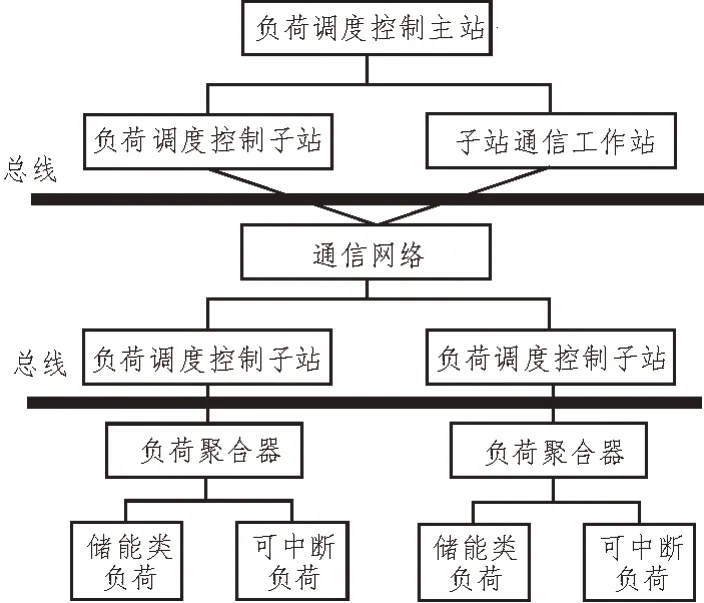
图2 系统硬件结构

由图2 可知，避峰负荷优化调控控制系统通过总线与主站交互，呈现分层分布式特点[8]。根据负荷调控时间维度，实时地与自动发电控制配合。

2.1 负荷数据集中器

负荷数据集中器具有多种串口、光以太网、无线通信接口以及测控、设备信息存取、转发、管理等多种功能，构成了下层设备的I/O 总线和通信总线[9-10]。其主要作用是实时采集电力负荷、开关量、室内温度、湿度等信息，并对电力负荷精确监控，实现了“四遥”的负载调度，即遥测、遥信、遥调、遥控，为系统提供集中处理数据。

2.2 负荷调控终端

用户负荷调控终端具备传统负荷控制终端的实时数据采集、本地功率控制、需求侧响应等功能，防止大规模电网意外地快速卸载。在智能变电站中，充分利用已有通信资源，建立了一种能够满足精确负载控制要求的多级点对点通信体系[11-12]。在三级结构中，主站接收来自更高一级的稳态控制系统负荷调度，并发布相应的控制任务；控制各子站点的卸载，并将其上传至主站，完成对主站的卸载指令；控制端实时传输用户可中断负荷，同时接收控制子站点的指令，使局部可中断负荷迅速被切断[13]。

3 优化调控技术

采用遗传算法在非连续、无规则或有噪音的情况下，得到更好的全局优化效果。在最优负载分配问题上，考虑到电站通常存在多个机组，而且每个机组的负载都是连续的，这是一种高精度多维连续负荷调控问题。在该问题中，采用两次避峰调控方式确定避峰时段。

3.1 初次避峰时段分组

在确保收敛性的前提下，运用平行搜索技术，通过自适应优化方法，获得最优个体[14]。尽管最初群体是随机产生的，但是最好的方法是使其能够满足限制条件，需要计算第k个用户组的第t时刻，可用于参与避峰调控的可中断负荷，公式为：

式中，min{qk(t)}表示用户在前一天的最小负荷值；qk(t)表示t时段的用户负荷。第t时刻避峰负荷总量按照式（2）进行计算。

式中，β表示所有用户组电量缺口占当前最大用电需求比例系数，基于此，对于初次分组的避峰选取在8:00-11:00、19:00-22:00 时段内[15]。

3.2 二次避峰时段分组

在遗传算法迭代时，要剔除优选者，其优劣评估函数就显得尤为重要。一个适当的评估值越高，越能够突出个体的优势，从而增加其遗传到下一代的概率，从而更有可能将其遗传到下一代。在求解过程中，使用遗传算法构建目标函数[16]。负荷最优问题是最小化问题，目标函数数值越小，个体越优秀，越有可能遗传到下一代。所以，不能简单地将目标函数视为适应度函数，而应将其倒数视为适应度函数，如下：

式中，fi(ai)表示第i个变电站的耗能；N表示变电站数量；ε表示惩罚系数。按照个人的适配性和被选概率的大小，计算当前个人被选出的概率为：

式中，qD表示指令负荷，能够将负荷约束问题转化为无约束问题：

在无约束问题支持下，整个调峰过程：当客户接到需求时，可以根据实际情况预处理负荷容量。生成二次分组，即控制组和后备组。最初的控制组是在主组之后，而后备组是空白的；根据二次分组的补充控制机制监督任务，每次分配完成后，查看用户是否配合；如果配合，就需查看调控情况。否则，继续发送避峰请求；查看调控是否结束，如果结束，则需终止，否则，继续发送避峰请求。基于此，对于二次分组的避峰选取在8:00-9:00、11:00-13:00、16:30-18:30、19:00-22:00 时段内。

4 系统测试

实验选取了100 个用户，采集这100 个用户的负荷数据，根据用户负荷频次特性，验证基于遗传算法的智能变电站避峰负荷优化调控系统设计的合理性。

4.1 测试装置

测试装置将MCU 电路模块作为整个电路核心，经过三个三端稳压器，可降低直流电源电压，实现对各种信息的处理和控制，其结构如图3 所示。

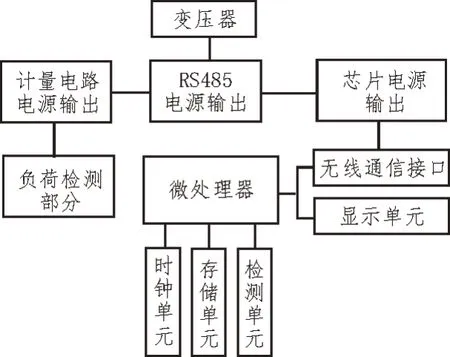
图3 测试装置

由图3 可知，通过实时检测智能变电站避峰负荷，获取相关负荷信息，并通过RS485 传输给单片机，再由单片机处理和存储获取的信息。

4.2 测试数据分析

测试数据来自某市电力公司2020 年11 月20 日每隔1 h 统计的负荷数据，实际负荷走向曲线如图4所示。

图4 实际负荷走向曲线

由图4 可知，用电高峰期分别为08:00-10:00、11:00-13:00、17:00-20:00，对于这些高峰期需要进行避峰负荷调控处理。理想情况下的避峰负荷调控结果如表1 所示。

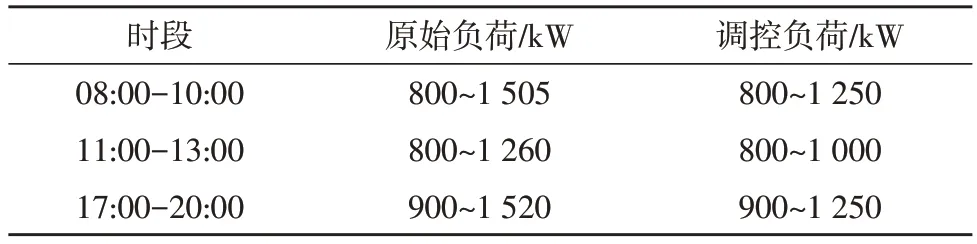
表1 理想避峰调控结果

由表1 可知，将原始负荷调控到理想负荷变化范围内，即为最优调控结果。

4.3 实验结果与分析

对比文献[1]、文献[2]和所设计系统的避峰负荷理想调控结果，如图5 所示。

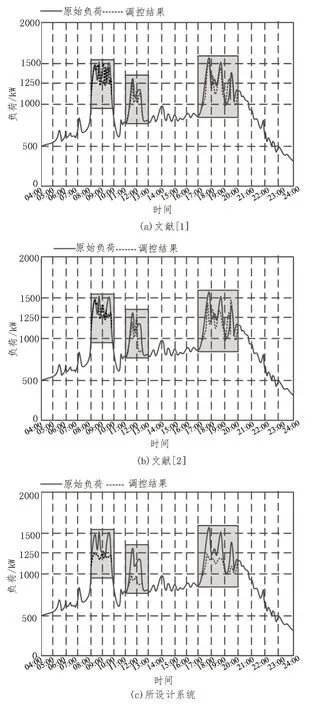
图5 三种方法避峰负荷理想调控结果

由图5 可知，使用文献[1]三个时间段的负荷调控范围分别为800～1 500 kW、800～1 257 kW、800～1 502 kW；文献[2]三个时间段的负荷调控范围分别为800～1 480 kW、800～1 200 kW、800～1 420 kW；设计系统三个时间段的负荷调控范围分别为800～1 250 kW、800～1 000 kW、900～1 250 kW。由此可知，设计系统负荷优化调控结果与理想结果一致。

5 结束语

通过二次分组，可以有效地解决大容量的智能变电站用户过度介入电网的避峰调节问题，实现不同调控方式下负荷调控效果满足用户需求。所设计系统解决了收敛性差的问题，具有较好的避峰负荷优化调控效果。