基于奇异熵的电网线路距离保护延时整定计算

周在阳，路建涛，李鹏云，张滇，陈仁明

（1.中煤西安设计工程有限责任公司，陕西西安 710001；2.合肥明信软件技术有限公司，安徽合肥 230000）

电网线路距离保护是电力系统中常见的一种保护方式，主要用于检测并隔离线路短路故障。为了有效地保护线路，距离保护装置需要在故障发生后尽快响应，控制断路器进行隔离，避免线路持续承载故障电流。而延时整定是距离保护装置的关键参数之一，指的是在检测到故障时，距离保护设备开始计时的时间。如果响应时间太短，可能会引起误动作；如果响应时间太长，则会延缓电网的恢复速度，影响电网的可靠性和供电能力。随着特高压电力系统架构的增强，特高压电力系统中的平行线路、短线路及环形网络呈现出较多的并线、双回线特点。在采用分段式匹配方式设置间隔的继电器时，不但操作极其复杂，且敏感性也很难满足规程要求。多电平间同时联动，导致工作时间延长，且易在系统中出现故障或中断故障，对系统的工作时间有很大限制，因此，需要适当简化系统。

文献[1]提出了基于测量阻抗轨迹的整定方法，以一种带可调阻抗环特性的线路间隔保护为例，利用保护故障前测量结果估计、动作区测量结果校正、动作区计算结果实时计算等方法，实现保护延时整定；文献[2]提出了基于双电压互感器的整定方法，在原始单个电压互感器基础上，再添加一个电压互感器组成一个保护单元，并通过测量母线两端的电量，实现对距离保护延时的调整和分析。

虽然当前微型计算机的技术已经比较完善，其运行的可靠性也有了较大的提升，但是仍会出现继电器拒动的情况，应用灵敏性不足。为此，提出了基于奇异熵的电网线路距离保护延时整定计算方法。

1 线路特征提取

小波奇异熵在电网线路特征提取过程中具有较好表征能力，电网线路输出信号经过小波包分解后，得到小波重构系数[3]。利用k层分解尺度，重构小波包能量系数，并将其表示为一个特征提取滑动窗，表达式为：

式中，L表示信号序列长度；H表示窗宽；α表示滑动因子。将每个滑动窗内所有小波重构系数均匀划分为N个区间，区间两两互不相交。基于小波奇异熵原理，分解某一时期的信号序列，并利用滑动窗口分布设定时间熵，其表达式为：

式中，Pk(Ck)表示第k个滑动窗中小波包能量系数落入Ck区间的概率。通过计算相应小波包时间熵，能够表征不同特征信号[4-5]。

基于此，提出一种基于卷积神经网络的潮流信号提取方法。卷积神经网络是一种具有多个特征提取结构的网络，其结构包括多张特征表，每张特征表上都有多个神经元，这些神经元之间的权重是相同的，被称作“卷积核团”[6-7]。由于采用卷积核，可以有效避免网络结构各个层次之间的过度匹配问题[8]。

电网潮流特征的提取由四个残差构造、两个卷积层、两个极大值池和一个整体均值池组成[9-10]。电网线路潮流特性的提取过程如下所示：

步骤一：搭建尺寸为N×N的灰度电网潮流框架；

步骤二：将残值的构造方法融入基本的卷积神经网络，在不提高网络复杂性的前提下，引入恒等保护的坡度方法，将其传递到下层，减轻过分层叠造成的“渐近”，并提高卷积网络各层间的信息量[11-12]。

步骤三：为有效控制模型数据量，提出了一种基于全局均值的多层次多目标优化方法，既可将多目标优化问题转化为特征点，又可解决因卷积函数误差引起的多目标优化问题[13]。将相应的特征点构成一个特征矢量，该特征矢量表示为：

式中，Q(qi)表示第i个电网潮流值；(xi,yi)表示电网所在位置坐标；m表示样本个数；x表示输入变量；Y(x) 表示输出结果；n表示电网潮流中元素个数。提取电网潮流元素，能够为电网潮流特征的提取提供支撑[14]。

将抽取到的特征量传送到分类器中，并将其归类保存。通过提取电网潮流特征，为电网安全稳定运行提供有力支持。

2 基于奇异熵的保护延时整定计算

2.1 电网信号稳定性分析

电网中通常存在多个并网逆变电源，为微电网提供了新能源接入环境，有效增强了微电网的柔性和灵活性，但其无机械暂态过程，因此在外界干扰下极易导致微电网不稳定[15]。基于此，引入有、无功误差的综合分量和交互式调节项，获得一种基于变换器的DG 系统的修正控制策略。利用奇异熵法精确地获取模态阶数，不论是否存在噪声，都可以精确地确定模态阶数，从而解决伪模、漏模的问题[16]。将该方法与奇异熵算法相融合，用于分析电网信号稳定性，过程如下所示：

利用实测或仿真得到的原始信号，构造数据矩阵，表示为：

式中，η表示实测次数。将奇异熵用于信号滤波，将区间时间引入低频震颤的分析中，并利用此方法对信号的模式进行了辨识，由此得到的信号奇异熵增量为：

式中，dab表示a、b两个信号之间的距离。

虽然该电网线路中存在大量的噪音，但是当有效信号达到饱和状态时，电网线路中的奇异熵值将很快地趋于由错误导致的奇异熵值。相对于有效信息的奇异熵增大来说，该收敛值一般都很小，所以当其随顺序改变时，将出现一个明显的拐点，该拐点所表示的顺序即有效信息的顺序。根据给定的模态阶数，将这两个空间分为信号与噪声两个子空间，使其最后一行与第一行被剔除，得到一个新的矩阵，并对其进行奇异熵值分解。根据模态辨识结果能够得到拟合数据，并将该拟合数据与实际数据之间的信噪比进行对比，公式为：

式中，x′表示拟合数据。通过计算信噪比，能够有效辨识信号数据和噪声数据，由此分析电网信号稳定情况。

2.2 电网线路距离保护延时整定计算

根据电网信号稳定情况，提出一种基于电网线路的安全可靠保护方案，使其灵敏度满足最小灵敏度要求。通过引入灵敏度因子进行调整，得到调整后灵敏度为：

式中，γ表示电网线路距离保护延时待整定段原始灵敏度；f(γ)表示调整函数。该函数根据实际整定经验可表示为：

式中，γmin表示灵敏度的最小值。为了确保安全性，在适当提高灵敏度之后，增大距离段的动作延时，并采用时间函数进行调整，公式为：

式中，tmin表示接地距离整定时间；Δt表示相间距离段整定时间。若待整定段原始灵敏度无法满足规程的灵敏度要求，那么应按阶梯调整保护时间，以此保证电网线路距离保护延时待整定段的灵敏整定。

3 实验

3.1 实验环境搭建及数据分析

搭建如图1 所示的实验环境。M1-M3 为3 个交流发电机，#1-#15 为15 段输电线路。#2、#3、#5、#6、#9、#10、#14、#15 为主输电线，因此更易出现整定延时。因此，选取#2、#3、#5、#6、#9、#10、#14、#15 作为实验的整定对象。

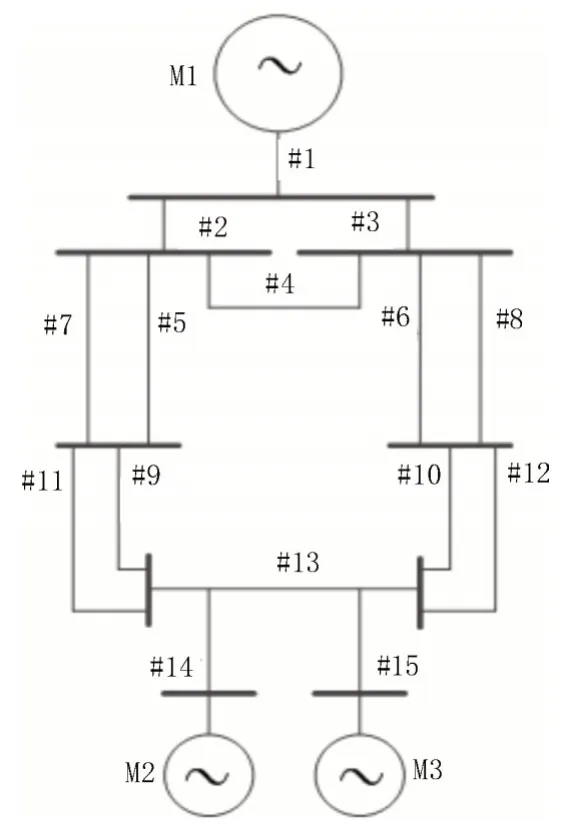
图1 电网运行环境搭建

电网线路距离保护主要用于检测并隔离线路短路故障，因此，该实验的线路故障类型为短路故障。当输电线路出现短路时，其电压为0 V。记录在检测到故障时，距离保护设备开始计时的时间，即为延时时长，实测数据如表1 所示。

表1 实测延时数据

根据表1 中的数据可知，#2、#3、#5、#6、#9、#10、#14、#15 输电线均发生了短路故障，均可用于电网线路距离保护延时的测试。

3.2 实验结果与分析

如果响应时间太短，可能会引起误动作；如果响应时间太长，则会延缓电网的恢复速度，影响电网的可靠性和供电能力。因此，设置最优延时为0.5 ms。将表1 数据作为标准，分别选取基于测量阻抗轨迹的整定方法、基于双电压互感器的整定方法和基于奇异熵的整定算法，对比分析延时整定效果，如表2所示。

表2 不同方法的延时整定效果对比

由表2 可知，基于测量阻抗轨迹的整定方法、基于双电压互感器的整定方法对延时整定后，故障检测延时缩短不够显著，应用效果还有待进一步提高。该文所提应用方法，延时得到明显控制，且整定结果与最优延时一致。

4 结束语

针对现有电网线路距离保护方法易受电网配置影响，存在灵敏性不足的问题，导致主保护不及时。为此，提出了基于奇异熵的电网线路距离保护延时整定计算方法。该方法在不改动保护配置结构的前提下可以获取更显著的安全效益。