基于数据驱动模型的智能风机失速故障辨识方法

李国俭，吴海军，王范华，韩冰，赵作飞

（1.国家电投集团内蒙古能源有限公司，内蒙古通辽 028011；2.内蒙古察哈尔新能源有限公司，内蒙古乌兰察布 011800）

在智能风机中，转动失速及失效是一种普遍现象。在工作负荷量较高的情况下，通道中的气体很可能发生离析，导致流体不稳，使得机械管道和管道中空气压力产生波动，从而导致设备受到一定损害。针对该问题，文献[1]提出了基于正交模态的失速辨识方法。对不稳定流场进行分解，识别出各种阶次的干扰模式，重建各个阶段模式的故障信号，通过傅立叶转换获得相应的频谱，识别出失速故障；文献[2]提出了基于M 序列的辨识方法。对某一变换器的两个输入、一个输出的转移方程进行了建模，并对建模结果进行了离散处理。利用二次测量信号与M系列三相位序列进行相位激励，获取相关的辨识结果。智能风机失速状态变化难以捕捉，影响到了故障辨识精度，因此提出基于数据驱动模型的智能风机失速故障辨识方法。

1 智能风机失速故障特征提取

通过对风机压力-流量特征进行分析，建立了局部失速与全失速判别函数，计算出固定流量系数、压力系数，通过不同故障模式空间映射分析风机失速状态的变化[3]。采用小波阈值降噪方法对重构信号进行小波包分解，结合小波包能量分析方法实现故障特征提取。

1.1 失速状态变化

当风机发生转动失速时，在叶轮的凹槽周围会产生涡旋漩涡。在不同的速度条件下，压力-流量特征群出现大量喘振流量点，连接这些点就会得到一个振荡边界线[4]。而在较高转速下，最大流量属于阻塞流量，能够在一个狭窄空间内产生失速与喘振。失速判断公式如下：

式中，Sa、S总分别表示失速涡横截面积和总横截面积。设失速极限值为δ′，如果δ＜δ′，那么风机部分失速；如果δ≥δ′，那么风机全失速[5]。无论是部分失速还是全失速，均存在固定流量系数和压力系数，分别用下述公式计算得出：

式中，ε部分失速、ε全失速分别表示部分失速和全失速流量系数；ς部分失速、ς全失速分别表示部分失速和全失速压力系数。智能风机失速故障喘振特征致使无法对失速故障特征进行精准辨识[6]。因此结合小波包分解提取故障特征。

1.2 故障特征提取

小波包分解是将小波分解成各层次的高频成分，其结果与小波相比具有更高的精度，能够在任意频率下对各频率进行分析[7-8]。基于小波包分解的故障特征提取流程为：

步骤一：在特征提取模型中输入正常数据矩阵E，该矩阵的数据窗口大小为2n，其中n表示多元变量维数。

步骤二：利用小波包变换处理数据矩阵中的数据变量，通过小波包分解获取变量分解结果，计算不同分解尺度下各个分量小波包能量值，结果如下[9]：

式中，t表示时间序列；Z表示一个非零实数；h(t)表示脉冲响应函数；αm表示第m个小波包分解层的分解结果。

步骤三：通过对每个子小波包主元进行了主成分分析，得到主元数目以及控制界参量[10]。

步骤四：将智能风机实时在线监测信号的输入和各成分进行小波阈值去噪处理，采用步骤二进行小波包分解[11]。

步骤五：计算每一个分量的小波包能量，结果如下：

式中，k表示尺度参数。

通过将原始信号与相应的小波包信号进行比较，得到信号的小波包能差值，结果为：

式中，E′k表示离线数据小波包能量。

步骤六：选取故障分量，采用与步骤三一样的方法建立主元模型，根据已知的控制限值进行故障特征划分[12]。

步骤七：在每个分量下，反复计算故障特征参量，并重复步骤四-步骤六，即确定部分失速和全失速故障特征参量，实现风机失速故障特征提取。

2 基于数据驱动模型的故障辨识

以故障特征提取结果为基础，利用数据驱动模型进行智能风机失速故障辨识，该过程是一个空间特征分析与映射的过程，如图1 所示。

图1 基于数据驱动的故障辨识

由图1 可知，基于数据驱动的故障辨识架构由数据空间、特征空间、趋势空间和故障模式空间组成，其中数据空间的各种数据通过数据融合后映射到数据空间中，数据空间将各种特征再映射到趋势空间，而趋势空间通过整合各种趋势映射到故障模式空间，以此实现智能风机失速故障辨识[13]。

数据空间到特征空间T1、特征空间到趋势空间T2、趋势空间到故障模式空间T3映射关系式如下所示：

式中，S1、S2、S3分别表示三个映射关系的融合单元；x1、x2、x3分别表示三个映射关系的输入变量；μ1、μ2、μ3分别表示三个映射关系的融合算子；y1、y2、y3分别表示三个映射关系的输出变量[14-15]。在风机失速故障特征明显的情况下，通过特征空间的映射将其转化为故障辨识模型参量进行故障辨识[16]。在风机失速故障特征不明显的情况下，从趋势空间中进行失速故障趋势辨识，获取故障趋势特征矢量，通过映射传递给故障模式空间，获取智能风机失速故障辨识结果。

3 故障辨识实验

3.1 风机选取

3.1.1 低压轴流送风机

低压风机压力-流量特性曲线如图2 所示。

图2 低压风机压力-流量特性曲线

由图2 可知，从D点开始减小风机流量，当压力达到极大值C点后，再逐渐减小，当压力达到极小值B点后，再逐渐增大直至A点完全闭合为止。

3.1.2 高压轴流送风机

高压风机压力-流量特性曲线如图3 所示。

图3 高压风机压力-流量特性曲线

由图3 可知，当流量从D点降低至接近临界值时，由于局部停滞区的增大，压力-流量特征曲线趋于平稳，当流量达到点B值时，在失速涡的作用下，流量突然跳至B1点，然后逐步升高至完全关闭状态A点。当完全关闭时，流量不会突然跳至B点，而会向C1 方向移动到达C点，这就是失速机制的双重特征。

3.2 失速信号频谱分析

通过实地考察，两台机组自开机到故障停止周期均比较短暂，前期运转较为顺利，但随着时间的增加，其振动幅度逐步增加，可以明显感受到机架的振动加重及噪声增加。选择低压、高压风机两组数据进行频谱分析。由于风机失速过程出现数据较多，选择0～120 s 数据为参考对象，统计实际故障频谱数据，如表1 所示。

表1 频谱实际数据统计

由表1 可知，低压风机失速比高压风机失速频谱变化范围要小，将此数据作为标准数据进行对比分析，以此保证实验结果具有科学性和可靠性。

3.3 故障辨识结果分析

分别使用基于正交模态的失速辨识方法、基于M 序列的辨识方法和基于数据驱动模型辨识方法，对比分析低压风机失速故障辨识结果，如图4所示。

图4 不同方法低压风机失速故障辨识结果

由图4 可知，使用基于正交模态的失速辨识方法频谱波动范围是690～4 600 Hz，使用基于M 序列的辨识方法频谱波动范围是0～4 000 Hz，使用基于数据驱动模型辨识方法频谱波动范围是0～1 100 Hz。只有使用所研究方法与表1 实际数据变化一致。对于高压风机失速故障辨识结果，如图5 所示。

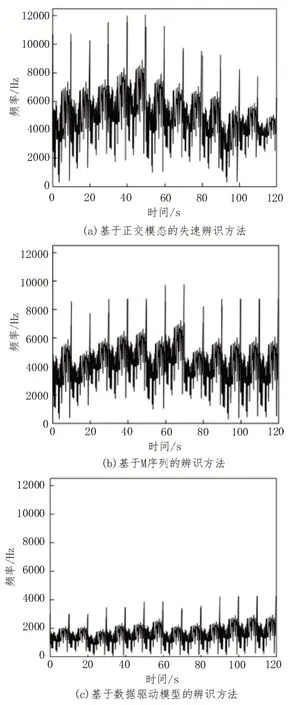
图5 不同方法高压风机失速故障辨识结果

由图5 可知，分别使用基于正交模态的失速辨识方法、基于M 序列的辨识方法和基于数据驱动模型辨识方法，频谱波动范围分别是200～12 000 Hz、200～9 000 Hz、0～4 200 Hz，只有使用所研究方法与表1 实际数据变化一致。

通过上述两组数据分析结果可知，所研究方法应用下的频谱变化数据与实际统计数据一致，说明该方法的故障辨识结果更为精准。

4 结束语

为了提升智能风机失速故障辨识精度，将数据驱动模型应用于实际低压、高压风机失速故障辨识过程中，以期为风机失速的精准辨识奠定坚实的基础。通过对机组的失速事故的研究，揭示了其失效机理及特点，通过合理地分析可以发现故障位置与原因，并针对其进行处理，从而防止故障再度发生，保证智能风机的安全稳定运行。