基于小波去噪和时频分析的智能电表量测数据挖掘研究

杨元，郭庆

（1.鄂尔多斯应用技术学院，内蒙古鄂尔多斯 017000；2.内蒙古自治区环境监测总站鄂尔多斯分站，内蒙古鄂尔多斯 017000）

智能电表可为用户提供实时的与有效的用电信息[1]，属于节能型智能化终端[2]。精准提取智能电表量测数据，可有效分析电网故障，提升用电的安全性和经济性[3]。因此国内许多学者提出相关研究。段晓萌等研究基于FP-growth 算法的用电异常数据挖掘方法[4]；倪家明提出基于时段特征匹配算法的智能电表用电预测方法[5]。虽然上述方法均能够满足实际需求，但对电表量测数据挖掘的准确性较低。为了解决上述问题，该文研究了基于小波去噪和时频分析的智能电表量测数据挖掘方法。

1 智能电表量测数据挖掘方法设计

1.1 小波变换的去噪方法

1.1.1 小波去噪流程

由于电力用户数量庞大、构成复杂，大量原始智能电表量测数据的复杂性和冗余度较高，需要根据提出的衡量准则，寻找对原信号的最佳逼近，以完成原信号和噪声信号的区分即应用小波变换阈值去噪方法对数据集实施去噪，去噪处理的流程图如图1所示。

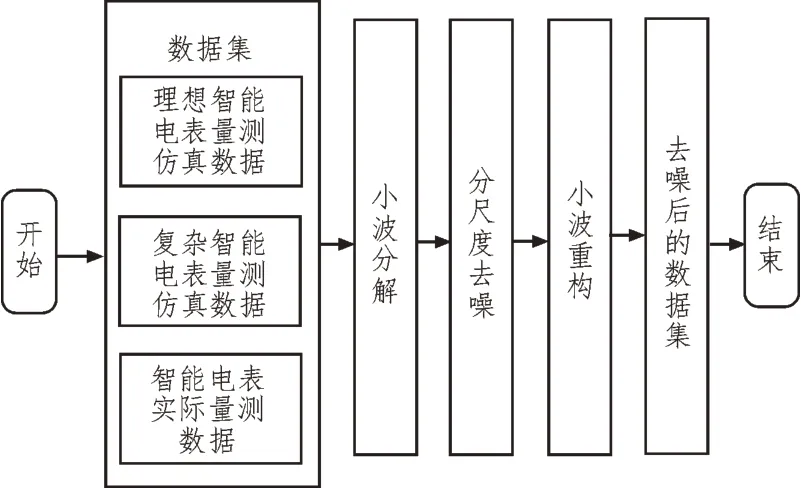
图1 去噪处理的流程图

选取合理的小波基与小波分解层数，小波分解数据集，获取小波分解数据集，获取小波分解的低频系数与不同分解层的高频系数；计算阈值，选择阈值函数，阈值处理分解获取的每层高频系数，获取处理后的小波系数；利用小波重构算法重构处理后的小波系数，完成数据集去噪[6]。

1.1.2 选择阈值

精准选取阈值能够提升小波阈值数据集去噪效果[7]，通过惩罚策略选择阈值，令小波系数B的数量是N，且0 ≤x≤N，阈值x的定义如下：

式中，Bk为小波系数内绝对值排序第k位的系数；σ为噪声的标准差，单位为dB；α为不低于1 的实数，通常情况下选择2；crit(x)选择最小值时相应的值是x*。通过惩罚策略选择的阈值是λ=|Bx*|。

1.1.3 选择阈值函数

阈值确定后，便可对存在噪声数据集的小波系数实施运算，获取去噪后数据集的小波系数；阈值函数代表去噪后数据集小波系数和存在噪声数据集小波系数间的函数关系，说明较好的阈值函数能够提升数据集的去噪效果[8]。去噪后数据集的小波系数软阈值函数数学表达公式如下：

式中，B表示存在噪声数据集的小波系数。软阈值函数数学表达公式如下：

式中，sgn(B)为符号函数。通过调整参数获得较优的小波系数的阈值估计，使其满足k值最大，即可获取最优阈值函数。

1.2 AORGK时频分析方法

AORGK（Analysis of Optimal Radial Gaussian Kernel）时频分析方法是通过短时模糊函数与随时间变化的自适应核函数，有效分离自分量信号与互分量信号，存在较好的时域与频域分辨率，精准挖掘智能电表量测数据[9]。利用AORGK 时频分析方法挖掘智能电表模型数据库内量测数据。

1.2.1 最优径向高斯核时频分析

量测数据s(t)的最优径向高斯核时频分布P(t,w)的表达公式如下：

式中，t为时间，单位为s；w为频率，单位为Hz；Z(θ,τ) 为模糊函数；φopt(θ,τ) 为最 优径向高斯 核函数；θ为频率偏差，单位为Hz；τ为延迟时间，单位为s。通过频率偏差与延迟时间组建模糊平面的横坐标与纵坐标[10-11]。Z(θ,τ)的表达公式如下：

式中，*为复共轭。随机剖面均为Gauss 型的二维函数是由径向高斯核φ(θ,τ)定义的，公式如下：

式中，ψ=arctan(τθ)为径向角，即径向和水平方向的夹角；σ(ψ)为在径向角ψ方向上，控制径向高斯核函数的扩展函数。核函数和量测数据相匹配，能够提升时频分布结果质量，便能求解最优的径向高斯核φopt(θ,τ)[12]；求解过程就是解决最优化问题，公式如下[13]：

式中，Z(r,ψ)为极坐标形式的模糊函数；φ(r,ψ)为径向高斯核函数。r=。利用核函数体积α 的选取阻止交叉项的干扰，通常情况下选择1 ≤α≤5。上述优化过程属于阻止交叉项干扰，只要确保自分量量测数据能够通过，即可完成量测数据的最小畸变。

1.2.2 AORGK时频分析

在时间发生改变时，AORGK 时频分析的核函数会出现自适应改变，AORGK 时频分析是在最优景象高斯核时频分析的基础上引入自适应核函数，获取随时间改变的自适应核函数的步骤如下：

步骤1：计算短时模糊函数（Short Time Ambiguity Function，STAF），公式如下：

式中，w(u)为对称窗函数，其中心位置是t。在|u|＞T情况下，对称窗函数w(u)=0，其中时间窗宽度是T。根据式（14）得知，Z(t),θ,τ仅计算中心为时间t，[t-T,t+T]范围中的量测数据，说明短时模糊函数能够精准描绘量测数据的任意细节部分[14-15]。在时刻t时，以短时模糊函数为基础，计算对应的AORGK的核函数φopt(t,θ,τ)，求解过程与式（11）、式（12）相近，因此获取量测数据s（t）的AORGK 时频分布的计算公式，公式如下：

通过AORGK 时频复制矩阵代表智能电表量测数据信息，表达公式如下[16]：

AORGK 时频方法挖掘的量测数据时频局部化分布特征结果是一个二维时频矩阵，这个二维时频矩阵各行代表这个频率点处量测数据随时间改变的分布规律，各列代表这个时刻量测数据随频率改变的分布规律。

2 实验分析

以某小区智能电表为实验对象，在该小区内随机选取10 个智能电表，利用该文方法对该小区智能电表量测数据实施挖掘，测试该文方法挖掘的准确性。同时选择基于FP-growth 算法的用电异常数据挖掘方法（文献[4]）和基于时段特征的匹配的智能电表用电预测方法（文献[5]）作为对比方法，记作方法1 与方法2。在获取该智能电表数据集后，根据小区配电电压10 kV 的输变电噪声信号特性，模拟出未经小波去噪的10 个智能电表量测数据的噪声频谱如图2 所示。

图2 未经小波去噪的噪声频谱图

根据图2 可以看出，所有智能电表量测数据都存在一定的噪声干扰，普遍在40～60 dB/A 区间内，可以证明当前噪声干扰着原始智能电表量测数据集。为解决这一问题，利用该文方法的小波去噪算法对智能电表量测数据集进行去噪。选取合理的小波基与小波分解层数，小波分解数据集，获取小波分解数据集，获取小波分解的低频系数与不同分解层的高频系数；计算阈值，选择阈值函数，阈值处理分解获取的每层高频系数，获取处理后的小波系数；利用小波重构算法重构处理后的小波系数，完成数据集去噪。去噪后的噪声分布情况如图3 所示。

图3 小波去噪后的噪声水平分布图

如图3 所示，在经过该文方法去噪后，10 个智能电表量测数据集的噪声分布均存在不同幅度的下降，处理后的噪声水平分布在340 dB/A 以下，且噪声分布得更加均匀，去噪效果较好。

为了进一步证明设计方法的有效性，对智能电表量测数据集加入20 dB 的白噪声，利用该文方法与方法1、方法2 对加入20 dB 白噪声的智能电表实施频率挖掘，信噪比是20 dB时，三种方法频率挖掘结果如表1 所示。

表1 信噪比是20 dB时，三种方法频率挖掘结果

根据表1 可知，在智能电表数据集中存在白噪声后，方法1 的相对误差最高可达11.76%，方法2 的相对误差最高可达20.27%。而该文方法的相对误差基本保持在2%以内。这是由于该文采用小波变换的去噪方法，能够精准去除数据集内的噪声，精准挖掘智能电表各分量频率。在该小区内选取1 000个具有局部时频化特征的智能电表有功功率信号，利用该文方法与方法1、方法2 挖掘不同数量的智能电表有功功率信号，以挖掘精度为测试指标，挖掘精度越高，方法的应用性能越好。三种方法的挖掘精度如图4 所示。

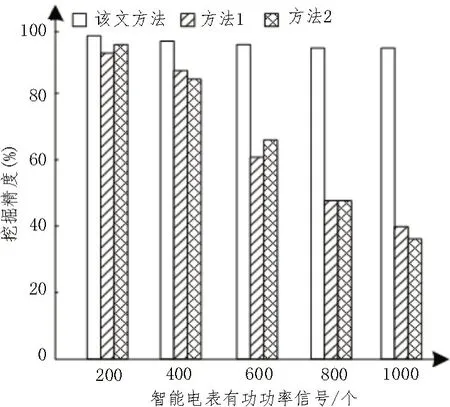
图4 三种方法的挖掘精度

根据图4 可知，随着智能电表有功功率信号的不断增加，三种方法的挖掘精度均逐渐下降，该文方法的挖掘精度下降幅度较小，在智能电表有功功率信号为800 个时，挖掘精度趋于平稳，始终维持在96%以上，其余两种方法的挖掘精度随智能电表数量增加出现大幅度下降，该文方法的挖掘精度均明显高于其余两种方法。实验证明，不同智能电表有功功率信号数量时，该文方法挖掘智能电表量测数据局部时频化特征的精度更高，这是因为该文利用小波变换阈值去噪方法去除智能电表相关量测数据的噪声，挖掘过程更具有针对性，挖掘精度更高，方法的应用性能较好。利用自适应最优径向高斯核时频分析方法，挖掘智能电表仿真模型数据库内数据，可以及时获取挖掘路径，提升挖掘效率。

3 结论

该文对基于小波去噪和时频分析的智能电表量测数据挖掘方法进行了研究。实验结果表明，所研究方法去噪效果较好，相对误差保持在2%以内，挖掘精度维持在96%以上，说明所研究方法能够精准挖掘智能电表量测数据，应用性能越好，能够为分析电能质量提供数据支持。日后，还可以挖掘智能电表量测数据为基础，引入电网故障分析方法，及时判断电网故障，提升电网运行的安全性与可靠性。