一类考虑空间异质环境的湖泊生态系统模型的全局稳定性

喻梦瑶,黄刚

(中国地质大学数学与物理学院,湖北 武汉 430074)

1.引言

水华现象是一种复杂的生态异常现象,其发生的原因较为复杂,水华现象发生的首要条件是在特定的环境条件下,海水或湖泊中某些浮游植物和浮游动物增殖达到一定的密度[1].继Riley等人[2]早期尝试模拟浮游生物之后,许多研究人员先后使用了不同复杂程度的数学模型来研究水华问题.这些模型中,其中一部分关注的是浮游植物与食草浮游动物之间的相互作用[3],另一部分则将营养浓度纳入模型进行了研究[4-6].

早期,通过假设浮游动物主要通过捕食浮游植物以保证自身的生长和繁衍,许多学者采用经典的Lotka-Volterra模型模拟浮游植物和浮游动物之间的捕食被捕食关系并进行广泛的研究.由于营养物质在浮游生物的生长过程中起着重要的作用,近些年来,很多学者将营养物质纳入浮游植物-浮游动物模型中,建立了营养物质-浮游植物-浮游动物三者相互关系的数学模型,并进行了广泛研究[6-8],例如,Hallam[7]研究了一类营养控制浮游生物模型家族的稳定性和持久性,得到了系统持久性的充分必要条件.水体中的有机物的存在与水体中浮游生物的繁殖、生长等有着密切的关系.水体中的有机物来源主要有两个方面,一是外界向水体中排放的有机物,一些陆地上的有机物可以通过地面径流汇入湖泊中,即外来有机物;二是生长在水体中的生物种群产生的有机物,即水体内部生成的有机物,水体内部生成的有机物一般在总的有机物中所占的比例很少.此外,研究发现枝角类和剑水蚤等浮游动物可以吸收来自陆地上的有机物[9],水蚤只靠外来有机物也能存活并繁衍后代[10].这使得外来有机物对浮游植物和浮游动物模型的影响受到了越来越多的关注,很多生物学家做了一系列的实验来探究外来有机物对浮游动物生长的影响.Tanentzap等人[9]总结了五个关于外来有机物和浮游动物的关系的假说,黄志伟等人[11]在其中三个假说的基础上,提出了一类包含外来有机物-浮游植物-浮游动物的数学模型,并对模型的动力学行为做了较为全面的分析.

湖泊是一个复杂的生态系统,它具备各种各样的功能对环境、动物以及人类生活都会产生一些影响,同时它会因为各种内部或者外部因素的影响而发生异变.例如,湖泊中水华的暴发就会导致湖泊生态系统异常,使湖泊生态系统的功能退化.因此,对湖泊生态系统的稳定性进行研究有助于我们更好的去保护湖泊生态系统.

事实上,浮游生物种群的状态不仅依赖时间还依赖空间,在许多生物系统中,被考虑的物种可能在空间上分散,也可能在时间上进化.本文在含有外来有机物的湖泊生态系统模型的基础上,假设外来有机物和浮游植物在空间分布均匀,进一步考虑了浮游动物的空间流动性.

考虑如下模型:

模型(1.1)中,C(x,t)表示外来有机物t时刻在空间位置x处的浓度,P(x,t),Z(x,t)分别代表浮游植物和浮游动物t时刻在空间位置x处的种群密度.k表示外来有机物单位时间内到湖泊生态系统的输入量,δ表示外来有机物沉入湖底的比率,参数βi(x),i=0,1,2,3,依赖于空间位置x,β0(x)表示浮游动物对外来有机物的摄取率.浮游植物满足logistic增长,这种增长率在文[12]中有过应用,β1(x)表示浮游动物对浮游植物的捕食能力.β2(x)表示浮游动物对浮游植物的吸收转化率,β3(x)表示浮游动物对外来有机物的吸收转化率.∆=是拉普拉斯算子,d(x)代表浮游动物在x处的扩散系数,m(x)表示浮游动物在x处的死亡率.Ω ∈Rn,n ∈N是一个有界开域,∂Ω是Ω的光滑边界,是Ω的闭包,v是在的单位外法向量.

近些年来,Lyapunov泛函的构造技术在流行病学、生态、时滞微分方程等方面都得到了扩展.NI等人[18]基于抛物型偏微分方程的异质性空间人口模型,提出了一类新型Lyapunov泛函研究了空间异质性扩散的Lotka-Volterra竞争模型的共存平衡解的全局稳定性,而后其他学者对之进行了扩展[19].

本文研究的湖泊生态系统模型不仅关注浮游生物种群随时间分布的情况,还考虑了浮游动物种群的空间分布.文章的其余部分的安排如下,第二部分论证了模型(1.1)的解的全局存在性和唯一性,以及模型的非齐次共存平衡解的存在性和唯一性.在第三部分利用Lyapunov泛函证明了模型非齐次共存平衡解的全局渐近稳定性.在第四部分通过数值模拟验证前面得到的理论结果.最后一部分给出本文的结论.

2.解的存在唯一性

在本节中,我们将首先分析模型(1.1)在初始条件(1.2)下解的全局存在性和唯一性,而后证明模型(1.1)非齐次共存平衡解的存在唯一性.

在分析解的全局存在唯一性前,做以下假设:

考虑如下系统:

其中,d(x),g(x)>0,λ(x)是上连续的正函数.通过文[13]中引理1的类似讨论,可建立如下引理.

引理2.1[13]模型(2.1)在C(,R)上存在唯一的正稳态u∗(x)并且是全局渐近稳定的.此外,如果λ和g都是正常数,则u∗=λ/g.

定理2.1对于任意给定的初始值ϕ=(ϕ1,ϕ2,ϕ3)∈Y+,满足条件(1.2)的模型(1.1)在[0,+∞)上有一个唯一的解U(t,ϕ)=(C(t,ϕ),P(t,ϕ),Z(t,ϕ))∈Y+,并且由(1.1)生成的半流Ψt:Y+→Y+定义如下:

此外,半流Ψt:Y+→Y+是点耗散的,且Y+对Ψt的有界子集的正轨道是有界的.

因此,将模型(1.1)可改写成如下积分方程:

这里,U(t)=(C(t),P(t),Z(t))T,得到

通过文[15]中的推论4可知,系统(1.1)有一个唯一的正解U(t,ϕ)=(C(t,ϕ),P(t,ϕ),Z(t,ϕ))在[0,τe)上,其中0<τe ≤∞.

接下来,我们证明模型(1.1)的局部解可以扩展为全局解,即τe=∞,只需证明解在Ω×[0,τe)有界.

令N(x,t)=C(x,t)+P(x,t),则有

故C(x,t),P(x,t)有界.

这里,β(x)=max(β2(x),β3(x)),根据假设(A2),引理2.1以及比较原理可知,存在一个常数M1>0使得

因此C(x,t),P(x,t),Z(x,t)在Ω×[0,τe)上有界,故定理得证.

接下来,我们证明系统(1.1)非齐次共存平衡解的存在唯一性.

考虑如下方程根据文[16]中的性质3.2和性质3.3,我们可以得到下面的引理.

引理2.2[16]如果f(x,w)=g(x,w)w,并且满足下面条件:

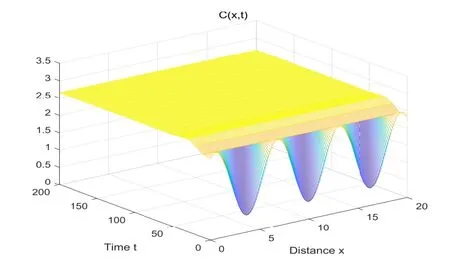
(i) 0

(ii) 存在K>0,使得当w>K时,有g(x,w)<0;

(iii) 当w>0时,g(x,w)关于w是严格递减的,那么方程(2.2)在t ∈(0,∞)时有一个唯一的正平衡解w∗(x).

定理2.2假设函数d(x),β0(x),β1(x),β2(x),β3(x)满足

那么,模型(1.1)存在唯一的正的非齐次平衡解(C3(x),P3(x),Z3(x)).

证如果(C3(x),P3(x),Z3(x))是模型(1.1)的共存平衡解,那么有

3.共存平衡解的全局渐近稳定性

在本节中,通过构造Lyapunov泛函得到了模型(1.1)的共存平衡解的全局稳定性.

定理3.1如果模型(1.1)中的系数满足条件(2.3),那么共存平衡解(C3(x),P3(x),Z3(x))是全局渐近稳定的.

证我们定义如下Lyapunov函数

V(t)沿着系统(1.1)的解的方向关于时间t求导,可得

运用(2.4)中的前两个方程,可得

由抛物方程解的有界性[18]及Sobolev嵌入定理,可知,存在一个常数C>0,使得

4.数值模拟

本节中,我们对系统(1.1)进行数值模拟,讨论系统中的部分参数在变化的情况下对模型解的动力学的影响.首先选定一维空间有界域Ω=[0,20],我们参考文[11]中的参数取值,假设系统中只有扩散系数受到空间异质环境的影响,其余参数均为常数的情况时,给定下列参数:

在系统满足上述给定的参数条件时,可以得出(C3,P3,Z3)=(2.66,0.29,2.97),并绘制出系统(1.1)解的时间演化图(图1),可以看出,当外来有机物的输入量控制为2.5时,随着时间增加,外来有机物、浮游植物以及浮游动物种群经过一段时间的演化,三者最终会达到共存并收敛到模型的正常数平衡态.对于浮游动物种群,当扩散系数为d(x)=x,x ∈[0,20],通过图1中浮游动物的种群密度随时间的演化可以看出,对于不同扩散系数,浮游动物的种群密度都会收敛到同一个正常数且不影响浮游动物达到收敛的时间.意味着浮游动物扩散系数的变化并不会改变浮游动物种群的稳定以及到达稳定的时间.

图1 系统(1.1)在参数满足条件(4.1)、(4.2)时, C(x,t), P(x,t),Z(x,t)的时间演化图

接下来,在浮游动物的扩散系数受空间异质环境影响的基础上,进一步考虑系统中的相互作用系数βi(x),i=0,1,2,3在变化的情况下对系统(1.1)中外来有机物的浓度、浮游植物以及浮游动物种群密度以及系统正平衡态的影响.

在模型的相互作用系数为(4.2)的基础上,进一步考虑空间异质环境的影响,对系统(1.1)中相互作用系数选取如下情况:

系统(1.1)中的其余参数及初始条件同(4.1)、(4.3).在满足参数条件(4.4)时,数值模拟的结果如图2所示,可以看出,当扩散系数和相互作用系数均发生变化时,浮游动物种群的时间演化不受到影响,外来有机物和浮游植物在空间异质环境的影响下,则会收敛到不同的平衡态.随着时间的发展,外来有机物、浮游植物以及浮游动物最终仍然会达到共存的状态,并且收敛到模型的正的非齐次平衡态.

图2 系统(1.1)在参数满足条件(4.1)、(4.4)时, C(x,t), P(x,t),Z(x,t)的时间演化图

5.结论

本文研究了一类具有扩散的外来有机物湖泊生态系统模型,模型引入了浮游动物的空间扩散并考虑种群间的相互作用系数是空间异质的.我们首先建立了系统(1.1)的解的全局存在唯一性,进一步得到了非齐次共存平衡解的存在唯一性,通过构造Lyapunov泛函证明了模型非齐次共存平衡解是全局渐近稳定的.最后,进行了一些数值模拟验证了理论结果.研究表明,通过控制外来有机物的输入量,使系统中外来有机物、浮游植物以及浮游动物达到共存的情况下,当选取浮游动物的扩散系数为d(x)=x时,浮游动物的空间异质扩散既不会使模型的共存平衡的稳态失稳也不会影响模型到达稳定的时间.而后进一步改变系统中的相互作用系数βi(x),i=0,1,2,3,外来有机物、浮游植物和浮游动物仍会共存,并最终收敛到系统的共存非齐次平衡态,上述结果意味着湖泊生态系统最终都会达到平衡状态,系统的结构和功能相对稳定,在受到来自外界的干扰后,具备一定的调节能力来应对外界的变化.