大跨度铁路斜拉桥索力快速识别方法研究

曹阳梅

(1.中铁第四勘察设计院集团有限公司,武汉 430063; 2.中国铁建股份有限公司桥梁工程实验室,武汉 430063)

拉索作为大跨度铁路斜拉桥的重要构件,是整个桥梁结构健康状态评估的重要因素之一。目前使用最多的索力监测方法为振动频率法[1],但其中拉索抗弯刚度的取值一直以来是个难题[2]。大量研究表明,拉索抗弯刚度是影响索力识别的重要因素[3-6],抗弯刚度折减系数因材料及运营条件不同,难以有统一的取值,传统算法一般采用全截面估算惯性矩及材料本身弹模值来确定,但由于拉索实质上为复合材料,并非规则截面,因而难以预先准确算出其抗弯刚度,进而导致索力识别工作精度不足。

目前,大多数学者通过变分原理[7-9]或能量法[10-11]建立考虑抗弯刚度的拉索结构偏微分方程,获得了索力解析公式或近似解公式,结果精确度得到较大提升。但由于公式及推导过程较为复杂,限制条件较多,需要一定修正后才能得到有效的结果,这种方式在工程实际应用时会由于拉索实际运营状态和理论假设有区别而带来一定误差,同时也因为算法的复杂性制约了抗弯刚度及索力识别的效率。此外,还有部分学者通过数值模拟[12-16]和试验方式[17-20]来获得拉索实际抗弯刚度,基于大量样本数据建立拟合关系或通过测量多级拉力水平下拉索频率,进而求解稳定的抗弯刚度。该方法虽然能较为精确地获得实际抗弯刚度值,但需要先基于大量实验操作过程获得测量值进而再进行实桥索力识别,且没有考虑实际索力对抗弯刚度的影响[21],不适用于已成桥的拉索索力测量。

一般而言,大跨度铁路桥梁天窗时间有限及上道条件苛刻,采用现场勘测来进行拉索状态识别的方式受到限制,且会对运营中桥梁产生一定影响,但大跨度铁路桥梁索力识别对桥梁结构运营状态的判断又十分重要。因此,本文提出一种简易可行的索力快速识别方法,基于拉索简支梁模型建立拉索频率、索力以及抗弯刚度的函数关系。在拉索长度和实测频率已知时,理论上有多组索力及抗弯刚度满足以上函数关系,再通过任意多阶已知频率下的变量交线则可进一步确定运营状态下拉索的唯一抗弯刚度和索力值,做到索力快速识别。工程实例表明,该方法一方面简易可行、精度较高,仅需采用拉索加速度振动测量设备即可,无需大量现场实验及计算过程,突破了传统抗弯刚度检测手段及场地限制,极大程度地减少了索力识别工作的繁琐性和成本;另一方面,该方法适用范围广,不受拉索边界条件和桥梁实际运营状态限制,不影响桥梁日常运营,可为后续大跨度铁路桥梁健康监测领域中索力长期监测的拉索抗弯刚度及索力识别工作提供参考。

1 理论方法

1.1 拉索常用动力学模型

1.1.1 张紧弦模型

张紧弦模型是最早应用于拉索动力学分析的模型,其将拉索模拟成一根水平张紧的钢丝。其公式如下[22]

(1)

式中,H为索力;m为拉索单位长度的质量;l为索的长度;ω为索的第n阶振动频率;n为索的振动阶数;E为拉索材料弹性模量;I为拉索截面惯性矩,下同。

1.1.2 简支梁模型

简支梁模型也是传统的索力换算模型及方法之一,该模型虽然考虑了弯曲刚度效应的影响,但由于拉索截面实质上为多种材料组成的复合截面,且截面参数(如惯性矩I等)与生产工艺、拉索状态等有关,因此难以预先给出一个准确值。其公式如下[22]

(2)

1.1.3 固结梁模型

考虑实际状态,拉索在锚具端部并非简支边界,而是会承受部分弯矩,当采用两端固结来模拟拉索边界时,其频率方程如下[22]

2αβ[1-cos(αl)cosh(βl)]+

(β2+α2)sin(αl)sinh(βl)=0

(3)

式中

由于该模型所对应的解析公式实质上为一个超越函数,现有手段并不能直接给出精确的解析解,但有大量研究基于工程实践经验及各种简化条件给出了固结梁模型的解析公式[23-24]。

针对上述3种模型对比分析,张紧弦模型是目前基于加速度传感器的索力测量方法中的常用公式,但实际上拉索会受到抗弯刚度、垂度、阻尼等多方面效应的影响,而该公式忽略了这些因素,导致换算索力值偏大。固结梁模型是目前最接近拉索实际边界状态的模型,虽然通过各种假设条件或近似解能大幅提高计算精度,但其计算方法复杂且有很多限制条件,不具备普适性。简支梁模型也是目前广泛运用的方法之一,方法中考虑了抗弯刚度效应的影响且原理简单、便于计算,因此本文选用简支梁模型为基准模型。

1.2 索力快速识别方法

以拉索长度、实测频率为已知条件,将索力、抗弯刚度设为未知数,代入式(2)中可得前n阶等式如下

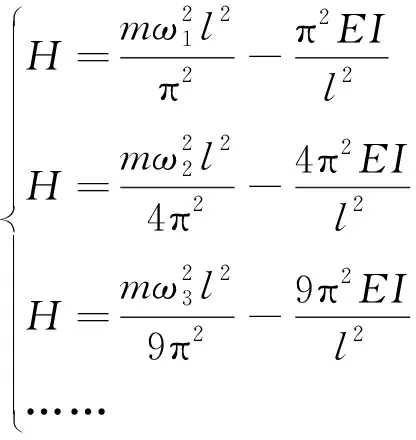
(4)

通过上述多个二元一次方程即可得到抗弯刚度的解,如式(5)所示,再将抗弯刚度代入式(4)即可同步得到索力值。

(5)

根据张紧弦模型易知,拉索的各阶频率呈几何倍数关系,由于拉索抗弯刚度的存在,实际拉索ωn/n并非是一个常数,且随着阶数的增加而单调递增。因此,由式(5)可知,理论上任意选取2阶模态即可得到抗弯刚度及索力唯一解,但由于抗弯刚度对频率的影响随着阶数越高越明显[25],因此,在应用中宜选取高阶频率进行计算,且阶数越多拟合结果越可靠。

2 抗弯刚度对索力计算结果影响分析

以某大跨度铁路斜拉桥工程为例,进行抗弯刚度及索力同步识别验证,该斜拉桥主桥设计为(40+88+252+88+40) m双塔双索面钢箱梁斜拉桥,共72根拉索,在4根边索上安装加速度传感器,传感器布置见图1。加速度振动时程图及频谱分析结果分别见图2及表1。

表1 各拉索前13阶频率值 HzTab.1 The first 13 frequency values of each cable

图1 斜拉桥拉索传感器布置示意(单位:m)Fig.1 Schematic diagram of cable sensor placement for cable-stayed bridges (unit: m)

图2 各拉索加速度振动及频谱分析结果Fig.2 Results of acceleration vibration and spectrum analysis of each cable

本桥斜拉索采用热挤聚乙烯双层护套的高强度平行钢丝拉索,标准截面如图3所示。斜拉索的两端均采用冷铸锚(张拉端锚具),除在斜拉索预埋钢管内设置橡胶减振块外,斜拉索在梁端采用外置黏性剪切阻尼器防风雨振。因此,拉索横断面并非规则截面,如采用全截面估算会导致抗弯刚度偏大,索力识别结果偏小;如不考虑刚度估算会导致抗弯刚度偏小,索力识别结果偏大。假设取全截面考虑抗弯刚度和不考虑抗弯刚度两种情况,按全截面考虑抗弯刚度的索力值为误差基准,以表1中各拉索最高阶频率计算索力,结果如表2所示。

表2 各拉索抗弯刚度对换算索力的影响Tab.2 Influence of flexural stiffness of each cable on converted cable force

图3 拉索横断面示意Fig.3 Cable cross section

由表2可知,抗弯刚度对该桥索力识别结果虽然相较成桥索力而言所占百分比不大,但其绝对值可达几百千牛,可能对索力监测结果带来较大误差,严重时甚至影响桥梁拉索结构在复杂运营状态下基本状况的判断。因此,拉索抗弯刚度的识别对于提高实测索力精度有重要意义。

3 工程实例

基于拉索简支梁模型,通过将两个无量纲设计参数(拉索的索力比H′/H和抗弯刚度比EI′/EI)视为连续自变量,其中H为成桥索力,EI为按全截面换算的抗弯刚度,H′为修正后索力,EI′为修正后抗弯刚度。可得到H′/H、EI′/EI以及ω三者之间的曲面图。对于实测各阶模态,用水平面ω=ωn去交做出的曲面可以得到一条交线,再通过任意多阶模态的交线投影则可进一步确定拉索的抗弯刚度和索力值。具体步骤如下。

第一步:基于设计成桥索力及拉索实测频率确定连续变量的合理范围,按一定步长Δ(H′/H)、Δ(EI′/EI)取值代入简支梁模型式(2)计算对应ω,建立三维曲面图。

第二步:基于实测加速度数据,得到前n阶实测频率ωn,用各阶水平面ω=ωn去交步骤一做出的曲面可以得到n条交线。

第三步:由于索力和抗弯刚度的唯一性,通过步骤二中的n条线放在同一平面再次相交,则可通过交点进一步确定唯一抗弯刚度和索力值。

以SLZD01拉索为例进行抗弯刚度及索力识别研究,图4给出了在前3阶实测频率与三维曲面交线,图5(a)给出了在前13阶实测频率下所有的H′/H和EI′/EI组合(即交线投影)。由于误差的存在,曲面和前4阶模态的交线并非严格交于一点,而5～13阶则较明显的交汇于集中区域,如图5(b)所示,取该交汇区域的中心(如有明显交汇点则取该点,如交汇于某区域则取该区域形心坐标)为抗弯刚度和索力的修正值。

图4 SLZD01拉索前3阶交线分析结果Fig.4 Analysis results of the first 3 crosslines of SLZD01 cable

图5 SLZD01拉索前13阶识别结果Fig.5 The first 13 recognition results of SLZD01 cable

计算表明,1～4阶频率规律性不强,这是因为抗弯刚度对频率的影响随着阶数越高越明显[25],本例刚好验证这一点。通过5～13阶高阶频率的交汇可以较为准确地找到唯一一组满足各阶频率的刚度和索力值,图5给出了修正后的抗弯刚度EI′为全截面理论估算值EI的0.46倍,随着所取阶数的增加,识别结果将更为准确。进一步的利用上述方法对其他3根SLZD02、SLZD03、SLZD04拉索进行抗弯刚度及索力识别,结果如图6所示。

图6 SLZD02、SLZD03、SLZD04拉索识别结果Fig.6 Identification result of SLZD02, SLZD03, SLZD04 cable

计算结果表明,排除低阶频率干扰后,各拉索通过高阶频率的交汇线可以较为准确地找到唯一一组满足各阶频率的刚度和索力值,SLZD01和SLZD02同为小里程侧,刚度折减系数分别为0.46、0.45,SLZD03和SLZD04同为大里程侧,刚度折减系数分别为0.37、0.35,同里程侧拉索规格完全对称,而用该方法的刚度识别结果也较为相近,验证了本文方法的准确性,可为类似规格拉索的抗弯刚度修正提供参考。

另一方面,利用本方法所得各拉索索力识别结果如表3所示,易知与按全截面考虑抗弯刚度的索力估算值相比,相对误差可降低5.22%,换算成绝对索力值可达254.45 kN,再次验证本方法有助于提高索力识别的准确性。

表3 本方法所得各拉索索力识别结果Tab.3 The identification results of cable force obtained by the method

4 结论

本文通过考虑拉索实际抗弯刚度来提高索力识别的精确度,基于拉索实测加速度数据得到各阶振动频率,建立实测高阶拉索频率、抗弯刚度、索力之间的三维变化曲线交点来识别抗弯刚度和索力的唯一值,总结了一种快速识别拉索索力的方法,主要结论如下。

(1)是否考虑抗弯刚度对本桥索力识别可带来8.48%的相对误差,绝对误差达413.5 kN,通过本方法识别的索力结果相对误差可降低5.22%,换算成索力值可达254.45 kN,有助于同类型大跨度铁路桥梁索力识别及状态评估工作。

(2)本方法中抗弯刚度对低阶频率不敏感,会导致较大误差,宜使用高阶频率进行分析,建议采用5阶及以上的频率,且阶数越多识别结果越精确。

(3)本方法仅靠拉索实测加速度振动数据即可实现计算,无需引入其他参数,可为实现大跨度铁路桥梁运营期索力长期监测工作提供参考。