基于广义柔度曲率信息熵的板式轨道脱空损伤识别

刘 渝，赵坪锐，徐天赐，刘卫星，姚 力

(1.西南交通大学高速铁路线路工程教育部重点实验室,成都 610031; 2.西南交通大学土木工程学院,成都 610031;3.中铁二院工程集团有限责任公司,成都 610031)

引言

板式轨道具有稳定性好、耐久性好、平顺性高、维修少等特点,被广泛应用于国内高速铁路中。随着板式轨道的服役时间增加,填充层损伤也相继出现,其中CRTSⅢ型板式轨道的自密实混凝土损伤较为突出。自密实混凝土CRTS Ⅲ型板式轨道的填充层,起着填充调整、承力传力的作用。轨道板脱空导致无砟轨道受力特性发生改变,影响行车舒适性和平顺性[1-3],因此,探索出一套适用于无砟轨道自密实混凝土脱空无损检测的方法至关重要。

基于振动的结构损伤识别指标具有损伤敏感性高、非损伤部位干扰小等优点,常用于混凝土结构损伤识别,这些指标包括:固有频率、振型模态、模态曲率、应变模态等。这些指标在国内外都运用于损伤检测中,并取得了一些成果。CAWLEY等[4]根据结构固有频率的变化对正方形铝板损伤进行了检测。薛江红等[5]提出对等优化模型对多脱层复合材料板进行了固有频率计算,探究了脱空长度、深度、位置对复合材料板固有频率的影响。向国荣[6]分析了轨道的固有频率随脱空大小的变化,脱空尺寸增大会使轨道固有频率减小。王盟等[7]结合时变模态振型和小波变换对悬臂结构以及特大桥模型进行损伤识别。PANDEY等[8]通过中心差分法近似模态曲率,利用模态曲率对板、梁结构损伤识别,并且模态曲率可以反映结构损伤程度。ZHONG等[9]利用模态曲率与二维平滑技术对板结构进行了损伤识别,结果表明模态曲率对板中和板边的识别均较为敏感。QIAO等[10]获取板结构模态曲率,并利用改进分形维数进行损伤识别。赵坪锐、胡志鹏等[11-12]针对板式无砟轨道CA砂浆损伤利用高斯曲率判断损伤以及定位损伤,采用差分近似计算高斯曲率无法得到板边测点的高斯曲率。任鹏、邢建伟等[13-14]运用应变模态分析梁结构的损伤特性。张晓东等[15]发现应变模态对轨道板裂缝与脱空识别较为敏感,提出了应变模态曲率差对轨道进行损伤识别,但实际工程中难以获取健康状态下的轨道应变模态曲率。

目前,已有学者将信息熵运用于结构损伤识别中。项长生等[16]使用信息熵对梁结构损伤进行识别。YANG等[17-18]利用信息熵对梁、板结构损伤位置进行检测。董家凡等[19]利用信息熵检测结构的损伤程度和位置,并通过实验验证了该指标的实用性。现有板式无砟轨道无损检测研究中,存在需要健康状态下获取轨道信息和仅针对大面积损伤检测等问题。信息熵具有高敏感性,且未用于板式无砟轨道无损检测。针对上述板式无砟轨道识别存在的问题,基于模态曲率指标在结构损伤识别中的优点,结合广义柔度矩阵、均匀荷载面、曲率和信息熵理论提出将ULS曲率信息熵用于轨道板脱空损伤识别,探究了脱空位置、面积、程度与ULS曲率信息熵的关系,以及ULS曲率信息熵对小面积脱空识别的敏感性。

1 轨道的广义柔度曲率理论

1.1 广义柔度矩阵

模态是结构的固有属性,通过动力测试能够得到结构的模态信息。许多学者用模态曲率对结构进行了损伤识别,其中通过柔度矩阵能够得到对结构损伤十分敏感的模态信息。轨道结构振动方程为

(K-ω2M)φ=0

(1)

式中,K为结构刚度矩阵;ω为结构模态频率;M为结构质量矩阵;φ为阶振型向量。对振型向量进行质量归一化处理,可得到结构模态柔度矩阵如式(2)。

(2)

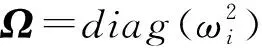
Fm=F(MF)m=ΦΩ-1-mΦT=

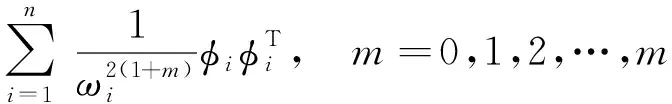
(3)

由广义柔度矩阵公式可得,越大的m,高阶模态的效果越小;当m=0时即为结构模态柔度矩阵,本文取m=1得一阶广义柔度矩阵如式(4)。

(4)

1.2 模态曲率

按照前面所述方法,计算得到轨道广义柔度矩阵。对广义柔度矩阵取对角线元素、计算其列向量无穷范数、计算其均匀荷载面构造出广义柔度对角矩阵FΔ、广义柔度无穷范数矩阵F∞、广义柔度均匀荷载面矩阵FU。荷载作用下结构位移可以通过广义柔度矩阵计算如式(5)。

w=F1P

(5)

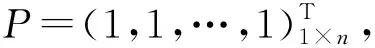
在结构完好无损时,结构的FΔ、F∞、FU为光滑的;结构发生损伤时,相应位置的FΔ、F∞、FU会出现微小突变。利用计算曲率可以定位损伤位置,通过中心差分法来近似计算曲率如式(6)。

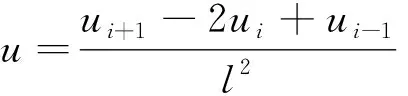
(6)

式中,ui-1、ui、ui+1为相邻点位移;l为相邻点的间距。

利用健康板式轨道和脱空板式轨道的模态信息提取出FΔ、F∞、FU并按照式(6)进行曲率计算得到FCΔ、FC∞、FCU,构造损伤识别指标GFΔ、GF∞、GFU,计算如下

(7)

(8)

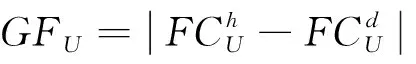
(9)

式中,上标h代表健康板式轨道;d代表脱空板式轨道。

2 损伤轨道曲率特征

2.1 模型建立

本文主要分析CRTSⅢ型板式轨道。实体单元能较好反映轨道结构的动力特性,参考文献[21-22]轨道结构和路基使用实体单元模拟,本模型采用实体单元。板式无砟轨道脱空处理采用布尔运算,将脱空区域的CA砂浆整个删除。模态分析得到轨道板表面振型竖向位移值,其中测点密度取0.2 m[11]。脱空位置示意如图1所示。其中,X、Y分别为脱空区域离轨道板角纵横方向上的距离;a、b分别为脱空区域的长宽;x、y分别为轨道纵横向。脱空工况如表1所示。

表1 轨道脱空工况Tab.1 Slab track void condition

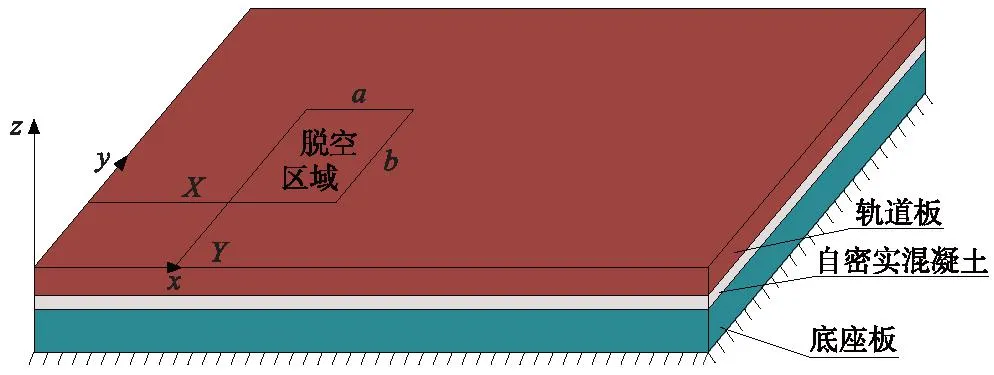
图1 轨道脱空示意Fig.1 Slab track void signage

2.2 损伤识别

高阶模态信息对广义柔度矩阵影响较小,所以提取轨道板表面一阶振型竖向位移值,仅对x方向求损伤识别指标GFΔ、GF∞、GFU,轨道损伤工况识别结果如图2～图4所示。结果显示,损伤识别指标均能较好地反映轨道脱空位置,并且可以显示出脱空损伤大致范围。三种工况的识别中,采取对角元素的GFΔ损伤指标相对GF∞、GFU效果差一些,峰值区域较为模糊。损伤识别指标GF∞、GFU在工况一、工况二、工况三均表现出较好的识别效果。由于均匀荷载面是在每个点施加单位荷载计算得出,因此损伤识别指标GFU相比GFΔ、GF∞在工况一～工况三中计算得到更大的数值。均匀荷载面曲率值较大,对轨道损伤识别效果较好,故下文使用均匀荷载面曲率计算信息熵识别轨道损伤。

图2 工况一 损伤识别Fig.2 Condition 1 damage identification

图3 工况二 损伤识别Fig.3 Condition 2 damage identification

图4 工况三 损伤识别Fig.4 Condition 3 damage identification

3 均匀荷载面曲率局部信息熵

3.1 均匀荷载面曲率

实际工程中难以获得健康状态下轨道模态数据,仅能获得损伤状态下轨道模态数据。计算工况一的均匀荷载面曲率FCU如图5所示。由于没有健康状态下轨道模态数据无法计算曲率差,可以看出,损伤引起的均匀荷载面曲率突变不易被发现,无法实现损伤识别。

图5 工况一均匀荷载面曲率Fig.5 Condition 1 uniform load surface curvature

3.2 均匀荷载面曲率的二维局部信息熵

SHANNON[23]提出信息熵概念用于表征系统信号复杂性,离散点信息熵计算如式(10)。轨道结构均匀荷载面曲率可视为一种波形信号,当轨道发生损伤时会导致均匀荷载面曲率局部突变,即损伤位置的曲率不再光滑。信息熵能够用来估计信号复杂性,信号变化缓慢时信息熵值较小,变化剧烈时信息熵值较大。健康状态下轨道均匀荷载面曲率连续光滑,整个变化是缓和的;损伤状态下轨道均匀荷载面曲率在损伤处发生突变,导致信息熵值改变。

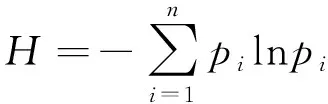
(10)

式中,H为信号的信息熵值;lnpi为信息量;pi为点Pi在信号中的概率。

信息熵是描述信号整体性,而轨道结构损伤为结构局部特征。整体信息熵无法对局部损伤进行表征,轨道脱空为块状,因此取一定范围的信号,计算二维局部信息熵[18]反映局部信号复杂性,对轨道结构损伤进行识别。二维局部信息熵计算如式(11)。

(11)

式中,H(Pij)为测点Pij信号的局部信息熵;N为范围内的信号个数。

信号范围的选取对二维局部信息熵计算有较大影响,特别在计算板角和板边均匀荷载面曲率信号时周围点的信号点缺失,选取过多的信号点计算局部信息熵会使得板角和板边信号点缺失更大,所以选取9个信号点计算二维局部信息熵。计算信号的选取如图6所示,其中黑色实心圆符号代表计算信号点,空心圆符号代表辅助计算信号点。因此,式(11)中各个符号分别为:均匀荷载面FCU、定位行向量Tr(i,j)、定位列向量Tc(i,j),fij表示轨道布点均匀荷载面曲率。

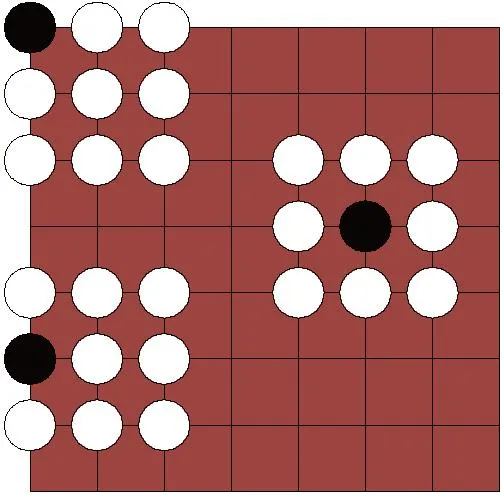
图6 计算信号点示意Fig.6 Calculation signal points schematic

由图5可知,轨道结构均匀荷载面曲率存在正负值,在计算二维局部信息熵时未损伤部位可能出现假峰值影响轨道损伤识别。为避免假峰值出现,将轨道均匀荷载面曲率矩阵加上整数倍的最小均匀荷载面曲率绝对值,使均匀荷载面曲率矩阵全为正值且不会影响其原有的光滑性。为验证均匀荷载面曲率的二维局部信息熵识别效果,计算工况一得到结果如图7所示。由图7可得,在轨道损伤区域出现峰值与峰谷,未损伤部分也存在不规则的凸起。为使信息熵更好地反映轨道损伤位置,对峰值采取单向处理得到单向ULS曲率信息熵,如图8所示。为避免未损伤部位凸起对识别效果的干扰,对采取单向化处理的均匀荷载面曲率信息熵的每一个值进行三次方处理,并做最大、最小标准化归一化处理,得到ULS曲率信息熵表征值损伤识别指标。

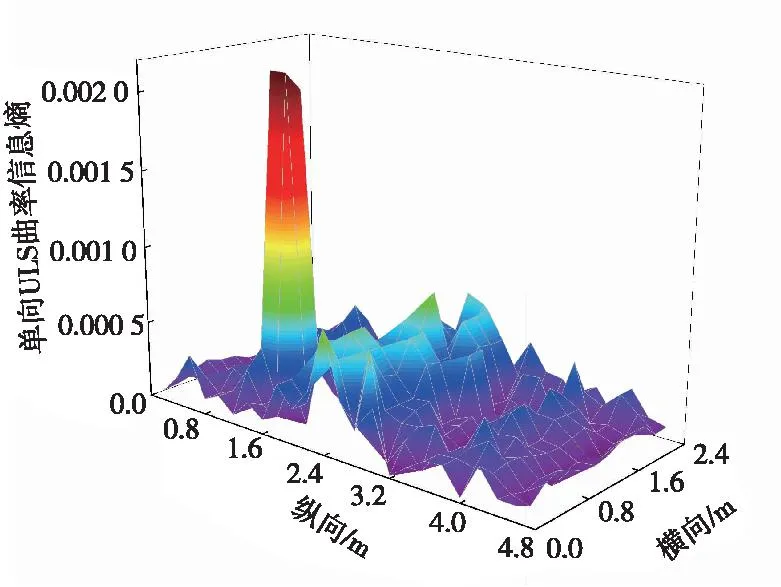
图8 单向ULS曲率信息熵Fig.8 Unidirectional ULS curvature information entropy

计算工况一、工况二及工况三曲率信息熵损伤识别指标如图9所示。由图9可知,ULS曲率信息熵表征值在损伤部位有明显的凸起,未损伤部分值较小不会影响轨道结构的损伤识别,并较为准确地反映脱空大小。ULS曲率信息熵表征值克服了无健康状态轨道结构模态信息进行轨道损伤识别。

图9 ULS曲率信息熵表征值Fig.9 ULS curvature information entropy characterization value

3.3 脱空位置、面积和高度与信息熵的关系

由于ULS曲率信息熵表征值是由ULS曲率信息熵归一化计算得到的,其中最大值均为1,所以分析归一化之前ULS曲率信息熵最值与脱空位置、面积、厚度变化的关系。

图10展示了ULS曲率信息熵与脱空区域中心位置的关系,其中由于轨道结构为对称结构,按对称位置在脱空区域中心距轨道边0.1,0.5,0.9,1.5,1.9,2.3 m取a为0.2 m、b为0.2 m进行脱空计算。从图10可以看出,ULS曲率信息熵关于轨道中心线对称,并且轨道边缘脱空ULS曲率值信息熵明显大于轨道内部脱空ULS曲率值信息熵。这是因为,轨道边缘相比内部约束更少,当脱空发生时曲率突变值更大,进而使ULS曲率信息熵增大。

图10 ULS曲率信息熵与脱空位置关系Fig.10 The relationship between ULS curvature information entropy and void location

考虑脱空面积对ULS曲率信息熵的影响,在分析脱空面积与ULS曲率信息熵时,取脱空区域中心距轨道边1.2 m,刚好位于轨道中心线上,且取a为0.2 m、b分别为0.4,0.8,1.2,1.6,2.0,2.4 m,如图11所示。由图11可以得出,ULS曲率信息熵随脱空面积增大而增大,脱空尺寸b从0.4 m增至0.8 m,2.0 m增至2.4 m时,ULS曲率信息熵变化较大,中间趋势较为平缓,原因是脱空区域轨道整体刚度减少使曲率出现突变,当脱空面积增大时刚度减少量增加。

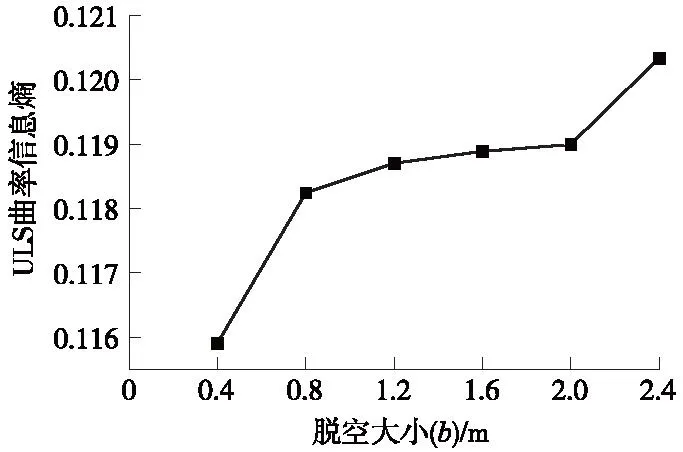
图11 ULS曲率信息熵与脱空面积关系Fig.11 The relationship between ULS curvature information entropy and void area

文献[24]中实测轨道脱空并非都为全厚度脱空,本文计算脱空厚度比例为0.2～1.0(步长为0.2)的工况ULS曲率信息熵,如图12所示。由于脱空厚度的增加导致轨道结构曲率局部峰值增加,使得ULS曲率信息值变大。

图12 ULS曲率信息熵与脱空厚度关系Fig.12 The relationship between ULS curvature information entropy and void thickness

3.4 识别敏感性分析

由于布置的测点数量有限且间隔为0.2 m,可能会对轨道小面积脱空损伤造成误判,及无法识别出小面积脱空损伤。为探究ULS曲率信息熵表征值对小面积脱空敏感性,分析脱空面积小于0.2 m×0.2 m时轨道ULS曲率信息熵表征值,由图10可得不同脱空位置的ULS曲率信息熵数值不同,所以分别取脱空位置1—X为1.25 m、Y为0.65 m;脱空位置2—X为1.25 m、Y为0 m,并且保证脱空区域并不位于测点上,取相同脱空大小a为0.1 m、b为0.1 m,分析得到两种工况的轨道一阶模态信息,计算出ULS曲率信息熵表征值,结果如图13所示。

图13 小面积脱空ULS曲率信息熵表征值Fig.13 Small area void ULS curvature information entropy characterization value

由图13可知,在板中位置和板边位置小面积脱空均能被识别出来,但在板中小面积脱空工况中轨道纵向中间位置未脱空区域出现假峰值。其原因在于轨道一阶模态均匀荷载面曲率为凸形曲面,而轨道纵向中间位置刚好位于凸形曲面,峰值存在曲率变化导致中部信息熵值较大。轨道板边相对轨道板中约束更少,当脱空发生时曲率突变更大,导致发生在板边的小面积脱空ULS曲率信息熵较大,在进行归一化时能够消除轨道纵向中部未脱空区域的假峰。

4 结论

本文通过计算板式无砟轨道有限元模型,结合广义柔度矩阵、均匀荷载面、局部信息熵等数据方法对轨道位移模态信息进行处理,得到以下结论。

(1)广义柔度曲率在轨道脱空区域出现局部峰值,利用脱空前后轨道模态信息计算广义柔度曲率差能够准确定位脱空位置。

(2)提出ULS曲率信息熵表征值轨道损伤识别指标,只需轨道损伤一阶模态信息,ULS曲率信息熵表征值能够有效定位轨道单处损伤以及多处损伤。

(3)在轨道对称位置上相同脱空的ULS曲率信息熵相同,ULS曲率信息熵对板边脱空更为敏感;ULS曲率信息熵随脱空面积和厚度增大而增大。

(4)轨道板板中脱空、轨道板板边脱空,ULS曲率信息熵表征值可有效识别;当测点密度取0.2 m时,对于0.1 m×0.1 m小面积脱空且脱空区域并不在测点上,ULS曲率信息熵表征值亦能表现出较好的损伤识别敏感性。