黏滞效应对带电粒子在双层二维电子气上方运动时受力情况的影响
史欣如,李春芝
(内蒙古民族大学物理与电子信息学院,内蒙古 通辽 028043)
在表面物理学中,学者们对带电粒子与二维电子气间的相互作用十分感兴趣[1-5],尤其是带电粒子的能量损失和二维电子气密度的扰动等[6-9]。若有带电粒子在电子气附近运动,电子气流体会因受到激发和电离从而发生扰动,而带电粒子却不断损耗能量。通过研究带电粒子与稠密等离子体间的相互作用中能量损失问题,可以探明高能量物理[10-13]和基础等离子体物理[7,14-15]中的粒子束输运过程的机理。近几年,在对WP2和GaAs的实验中所表现的很多特性证明了电子气流体具有黏性,且有一系列新的理论用来研究电子气的黏性流体特性[16-19]。同时,黏性量子流体动力学模型(QHD)被用来研究量子半导体器件[20-22]、非线性等离子体振荡[23]和稠密黏性量子等离子体的Jeans自引力不稳定性情况[24]。CHEN等[25]通过采用线性化黏性量子流体动力学模型研究了带电粒子在单层二维电子气附近运动时的阻止力,笔者将在此基础上进一步研究黏滞系数对带电粒子与双层二维电子气作用时的影响。全文采用了高斯单位制(厘米-克-秒)。
1 理论模型
双层二维电子气(2DEG)是由石墨烯构成的且分别位于z=0(平面1)和z=d(平面2),其他区域(z≠0,z≠d)为真空,d为2个平面之间的距离。带电量为Z1e的粒子沿x轴方向运动情况见图1。

图1 带电量为Z1e 的粒子沿x 轴方向运动Fig.1 A particle with charge Z1e moves along the x-axis
如图1所示,在没有受到外界电场作用时,石墨烯平面内可以向各个方向移动的自由电子密度等于近乎静止不动的离子密度,即ne0=ni0=n0。考虑在双层石墨烯平面的上方存在一个载能粒子,该粒子带电量为Z1e,以不随时间变化的速度v=ve^x在2个平面上方沿x轴方向运动,该载能粒子的密度可表示为ρext=Z1eδ(r-vt)δ(z-z0),其中z0(z0>d)是粒子与平面1的距离,此时均匀的电子气将发生微小扰动,其速度场为ue(r,t)=uej(r,t),电子气密度为ne(r,t)=n0+nej(r,t),uej(r,t)代表着电子气流体的速度,nej(r,t)代表着电子气流体密度的一阶微扰(j=1 对应着平面1,j=2 对应着平面2)。引入含有黏性修正项的线性化量子流体动力学模型[23],则2个平面内的电子气满足的线性化连续性方程
动量平衡方程
和Poisson方程
其中me是电子质量,e是基本电荷,ℏ 是普朗克常数除以2π,Φtot=Φext+Φind,Φext是由入射粒子激发的库仑势,Φind是2 个平面内电子气密度扰动所激发的感应势。在方程(1)~方程(3)中,梯度算符在方程(2)中,等式右端各项分别表示电场力、电子气内部因简并引起的压力、电子气内部电子之间的相互作用力、平面内不动的正电荷背景与自由移动的电子之间的摩擦力(γ是摩擦系数),而最后一项则是在不同速度下电子气流体产生的黏滞力,η为黏滞系数。
需要说明的是,在流体动力学状态中,电子动力学特性主要由流体的黏度决定,而不是杂质散射[26],在不考虑温度效应情况下,黏度主要由流体中的动量弛豫矩描述,黏滞系数η与二阶弛豫时间τ2成正比。
其中vF为费米速度,1/τ2,ee(T)为电子间弛豫率,而1τ2,0为剪切应力在温度T→0 时的“残余”弛豫率。若不考虑温度对弛豫率的影响,则τ2≈τ2,0。此外,τ2还与物质密度有关,而Wigne 半径rs=(2πn0a2B)-1/2也取决于描述材料特性的密度的函数,因此,τ2的值可以通过给出密度函数rs的值来获得[27]。在rs=2 时,τ2≈τ2,0的值可以取在1.1×10-16~1.1×10-3s 之间,与此对应的黏滞系数在0.33 ~330.00 cm2/s 之间,该范围内的黏滞系数可用来研究密度为n=1012cm-2量级的石墨烯中的电子气流体[23]。因此,在以下的计算中主要研究黏滞系数为η=0.33 cm2/s、η=3.30 cm2/s、η=33.00 cm2/s 和η=330.00 cm2/s 的情况下石墨烯的电激发状态。
引用傅立叶变换:
此外,入射粒子所受的阻止力Fs(v),其负值也称为阻止本领,即粒子运动方向单位长度上的能量损失;Fz(v)为侧向力,其方向指向石墨烯平面,该力使入射粒子的运动轨迹有向石墨烯平面偏转的趋势。这2个力的表达式可以通过对式(9)中感应势Φind(r,z,t)在不同方向求梯度得到:
为计算方便,引入无量纲参量:ky/kF→ky,k/kF→k,ω/ωp→ω,v/vB→v,γ/ωP→γ,η/(ωp/k2F)→η,l/λF→l,其中l为长度,λF=1/kF是Fermi波长,vB=e2/ℏ ≈c/137 是波尔速度,c为真空中的光速。
在下述的数值模拟中,假定入射粒子为质子,即Z1=1,Wigner半径为rs=2,摩擦系数为γ=0.02ωp。入射粒子与平面1之间的距离为z0,2个平面之间的距离为d,而入射粒子速度v和黏滞系数η是变化的。需要说明的是,由ωp/kF=vB和,因此,当η=0.33 cm2/s 、η=3.30 cm2/s 、η=33.00 cm2/s 和η=330.00 cm2/s 时,由η/(ωp/k2F)→η无量纲化后的黏滞系数分别为η=0.142,η=1.420,η=14.200 和η=142.000。
2 计算结果与分析
2.1 感应电子气密度
在图2(a)~图2(c)中,分别计算了速度v=2.0vB、2.5vB、3.0vB时,不同黏滞系数η=0.000、η=0.142、η=1.420、η=14.200 和η=142.000(已用ωp k2F无量纲化)下ne2(已用n0无量纲化)沿x轴方向的变化情况。其中取d=3.0λF,z0=6.0λF。
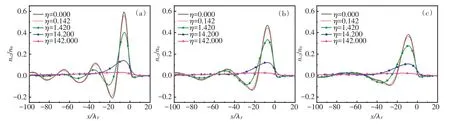
图2 黏滞系数对ne2(已使用n0 无量纲化)沿x 轴方向变化的影响Fig.2 The effect of viscosity coefficient on ne2(dimensionless by n0)the variation along the x-axis direction
从图2(a)可以看出,当入射粒子速度一定时,随着η的增大,ne2振荡的幅值和区域均变小,说明黏滞系数对石墨烯中电子气的扰动起到了抑制作用,这是由于入射粒子的部分能量被电子气流体的黏滞效应所耗散,导致只有少部分能量使电子气扰动。随着黏滞系数的增大,耗散的能量增多,从而电子气扰动变弱。从图2(b)和图2(c)中可以看出,随着速度的增大,ne2振荡的幅值变小,波长变大,说明粒子运动速度越快,其库仑场使电子气激发或电离的能力变弱,换言之,就是电子气还来不及响应,带电粒子已经远离了。
图3(a)~图3(c)分别计算了速度v=2.0vB、2.5vB、3.0vB时平面1内感应电子气密度沿x方向的变化情况,所选参数与计算ne2时相同。对比图2和图3时发现,ne1振荡的幅值远小于ne2振荡的幅值,这是由于平面2对入射粒子的静电屏蔽作用导致的。图3(a)显示,当入射粒子速度一定时,随着黏滞系数的增大,电子气振荡的幅值和区域迅速减小,说明黏滞效应的存在,能够使平面1内电子气扰动的电场力大部分被耗散掉,仅有少部分使其发生扰动。从图3(b)和图3(c)可以看出,随着v的增大,电子气振荡的幅值变小,波长变大,这一点与ne2的振荡特征一致。
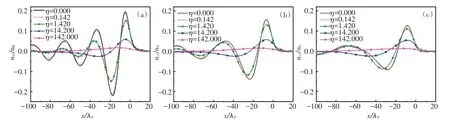
图3 黏滞系数对ne1(已使用n0 无量纲化)沿x 轴方向变化的影响Fig.3 The effect of viscosity coefficient on ne1(dimensionless by n0)the variation along the x-axis direction
2.2 侧向力和阻止本领
通过计算分析,不同黏滞系数对载能粒子所受的阻止力以及侧向力的影响见图4。取d=2.0λF,z0=3.0λF,由图4(a)知,当v<0.6vB,若不考虑黏滞效应的影响(η=0.0),FS(v)近乎为零,说明v较小时,其前方和后方的电子数近似相同,不会产生向后的感应电场。若考虑黏滞效应的影响,则粒子所受的阻止力不能忽略,说明黏滞效应阻碍电子对入射粒子向前运动的响应,从而产生向后的感应电场。随着入射粒子速度的增大,与不考虑黏滞效应的情况对比,黏滞系数越大,阻止力越小,说明黏滞效应项对电子气的扰动起到了抑制作用,导致向后的感应电场变弱,阻止力变小,这一点可以从图2和图3中ne2和ne1受黏滞系数影响中看出。对于侧向力,由图4(b)知,在v<1.5vB时,黏滞效应越大,Fz(v)越小,这是由于黏滞效应抑制了电子气的扰动,从而使感应电场变弱所导致的。当入射粒子的速度v>1.5vB时,黏滞效应对侧向力的影响变小并逐渐消失。

图4 不同黏滞系数对阻止力FS(v)和侧向力Fz(v)(已用F0=e2/a2B 无量纲化)的影响Fig.4 The influence of different viscosity coefficients on stopping force FS(v) and lateral force Fz(v)(dimensionless by F0=e2/a2B)
3 结论
笔者采用含黏滞修正项的线性化量子流体动力学模型研究了黏滞效应对双层石墨烯平面静电激发状态的影响。结果表明,黏滞系数越大,电子气振荡的幅值和区域变小,波长变大。对阻止力,在速度较低的区域,黏滞系数越大,阻止力越大,而在速度较高的区域阻止力却随着黏滞系数的增大而减小。此外,对侧向力,在速度不大的情况下,黏滞系数越大,侧向力越小,当速度略增大时(v>1.5vB),黏滞效应对侧向力的影响逐渐变小并消失。

