基于ANSYS的简支梁车-桥-支座耦合动力响应分析

宁 锋, 邓年春

(1.中交四航工程研究院有限公司, 广州 510415; 2.广西大学土木建筑工程学院, 南宁 530004;3.中交集团交通基础工程环保与安全重点实验室, 广州 510415; 4.广西防灾减灾与工程安全重点实验室, 南宁 530004)

随着桥梁建造和交通运输的高速发展,桥梁与车辆之间的振动问题愈发突出,车桥产生的振动不但会影响桥梁结构的安全性和耐久性,而且会影响行车安全,引发交通事故[1-4]。在以往的车桥耦合振动研究中,通常采用生死单元和自由度耦合就可以对简化的车桥模型进行车桥耦合振动分析,但这种方法计算精度较低,且要求车辆行驶工况和桥型简单。如今基于计算机技术的有限元分析方法飞速发展,车桥耦合振动的研究也进入了新阶段。刘永健等[5]刘世忠等[6]结合分离迭代法原理与车辆动力学理论,提出一种基于ANSYS的车桥耦合振动响应数值分析方法,计算结果和相关文献算例有较高的吻合度,并以此方法分别建立车辆与桥梁子系统,分析双层公路钢桁梁桥在车桥耦合振动下的影响;许汉铮等[7]基于ANSYS精细化建模,在研究车辆的横竖向振动对曲线桥振动的影响中表明车桥耦合振动主要为竖向振动,建议分析曲线桥动力响应时应考虑车桥耦合作用;韩智强等[8]、韩智强等[9]采用模态综合法建立多车车桥耦合系统,研究多点激励和桥面不平度对车桥耦合振动的影响,结果表明部分国家冲击系数规范值较小,建议在研究车桥耦合振动问题中考虑多点激励和桥面不平度的影响;王秀丽等[10]采用隐式动力学分析了大跨度钢管翼缘组合梁桥车桥耦合振动的影响,结果表明路面平整度、车辆载重和速度对车桥耦合振动均有较大影响;Liu等[11]采用有限元方法建立车辆处于交通拥堵怠速时车桥耦合模型,分析交通拥堵对桥梁的动力响应影响,表明交通拥堵情况下车桥耦合对桥梁造成的影响远大于正常交通条件下的影响。

桥梁支座作为桥梁的重要传力构件,其刚度和阻尼对桥梁振动的影响不容忽视[12-15],上述提出的车桥耦合振动分析方法均未考虑弹性桥梁支座对车桥耦合振动的影响,因此在刘永健等[5]、刘世忠等[6]的分析方法的基础上,结合分离法与汽车动力学原理,在ANSYS软件中通过APDL编程把车辆模型、桥梁模型和支座模型分别独立建立,再通过APDL编写车辆、桥梁和支座之间的位移协调关系和力的平衡关系进行车-桥-支座耦合,以一座30 m简支箱梁桥为算例,对车-桥-支座耦合系统进行了动力响应分析。

1 车-桥-支座耦合动力计算模型

把车-桥-支座系统分为车辆、桥梁和支座3个子系统建立各自的运动方程,通过接触点处位移协调和相互作用力的平衡关系分别把车辆-桥梁和桥梁-支座进行耦合,形成车-桥-支座耦合系统模型如图1所示,再采用迭代法求解系统响应。车辆模型采用9自由度(车体的浮沉、点头和侧倾和各个车轮的竖向位移自由度)空间整车模型如图2所示。系统的整体坐标系为OXYZ,把车体看作质量为M的刚体,其点头自由度θ和侧倾自由度φ的转动惯量分别为Ix和Iy,通过悬架弹簧和减振器把车体质量与车轮质量连接;各车轮的质量为mi(i=1,2,3,4,5,6),各车轮竖向位移自由度分别为zi(i=1,2,3,4,5,6),车轮再通过具有一定刚度和阻尼的弹簧(轮胎)与桥梁路面连接,弹簧(轮胎)与桥面接触位置点为Ni(i=1,2,3,4,5,6)。

图1 车-桥-支座耦合系统模型

图2 三轴空间整车模型

1.1 车辆运动微分方程

由达朗贝尔原理[12]可推导出整车运动微分方程:

(1)

式中:Mv、Cv、Kv、Fvb、uv分别为车辆的质量矩阵、阻尼矩阵、刚度矩阵、荷载矩阵和位移矩阵,具体表达式如下:

(2)

(3)

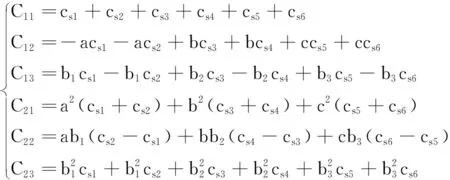
(4)

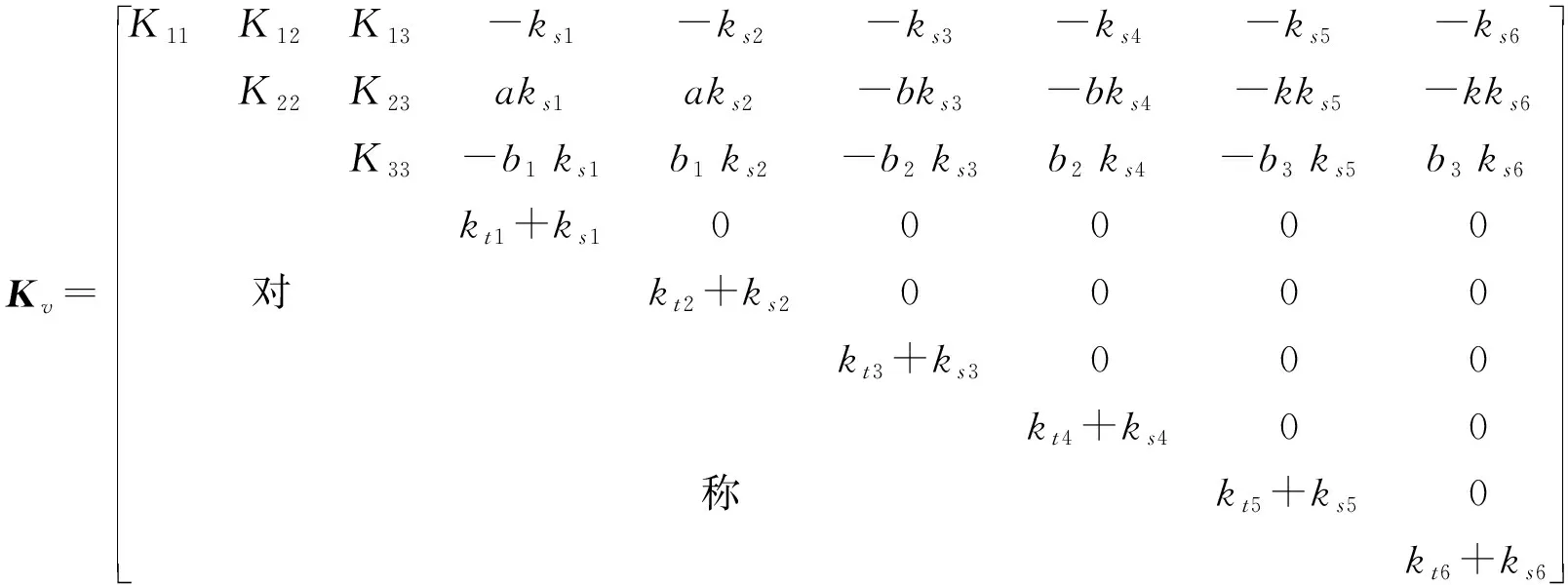
(5)

(6)

uv=[zvθvφvzw1zw2zw3zw4zw5zw6]T

(7)

Fvb=[0 0 0kt1zr1kt2zr2kt3zr3

kt4zr4kt5zr5kt6zr6]T

(8)

式中:mv、Ip、Ir分别为车体质量、点头转动惯量和侧倾转动惯量;mi(i=1,2,3,4,5,6)为车轮质量;ksi(i=1,2,3,4,5,6)为悬架刚度系数;csi(i=1,2,3,4,5,6)为悬架阻尼系数;kti(i=1,2,3,4,5,6)为轮胎刚度系数;cti(i=1,2,3,4,5,6)为轮胎阻尼系数;zv、θv、φv分别为车体竖向位移、点头角位移和侧倾角位移;zwi(i=1,2,3,4,5,6)为车轮的竖向位移;zri(i=1,2,3,4,5,6)为车轮对应的桥梁接触点的竖向位移;b1、b2、b3分别为1/2前中后车轴轴距;a、b、c分别为前中后车轴与车体重心的距离。

1.2 桥梁结构振动方程

根据有限元动力学理论[13]可以得到桥梁振动的一般方程:

(9)

桥梁结构的阻尼矩阵可以表示为:

Cb=αMb+βKb

(10)

式中:

(11)

式中:α、β为质量阻尼系数(α阻尼)和刚度阻尼系数(β阻尼);ωi、ωj分别为桥梁结构的第i和第j阶振频;ξi、ξj分别为桥梁结构的第i和第j阶振型对应的阻尼比。

1.3 支座振动方程

支座振动方程表示为

(12)

其中橡胶支座的法向刚度系数Kp和阻尼系数Cp分别由以下公式确定。

(13)

(14)

式中:S为橡胶支座的形状系数;a、b为橡胶的边长,m;te为单层橡胶的厚度,m;E为橡胶支座的等价弹性模量;Gd为橡胶支座的动剪切模量,kN/m2。Fp为阻尼力;Vp为支座运动速度。

2 车-桥-支座耦合关系

在车-桥-支座耦合系统中,车辆系统与桥梁结构通过接触点处的位移协调关系和相互作用力的平衡关系进行耦合。

1)位移协调关系

在车辆行驶过程中,假定车辆轮胎与桥面、支座与桥面和支座与桥墩之间始终紧密接触,均不发生跳车或脱空现象。其位移协调关系表示为

Δi=zi+ri-zbi

(15)

(16)

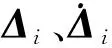
2)力学耦合关系

无论是桥面与车轮接触点之间,还是支座与桥面接触点或桥墩接触点之间,都存在一对相互作用的力,这对相互作用的力总是大小相等、方向相反,可表示为

(17)

式中:Fti为第i个接触点的车-桥或桥-支座接触力;kti、cti为第i个轮胎或支座的刚度系数和阻尼系数。

3 车-桥-支座耦合动力响应分析

以计算跨径为30 m的等截面简支箱梁桥为算例,其中箱梁为C50混凝土,弹性模量为3.45×107kN/m3,泊松比为0.2,密度为2.549 kN/m3/g,截面为单箱单室截面,截面面积为11.298 7 m2,截面抗弯刚度为13.532 1 m4。采用ANSYS中的APDL参数化建立有限元模型如图3所示。

图3 有限元模型

3.1 桥面不平整度的影响

根据中国国家标准《车辆振动输入与路面平度分析工况:单辆三轴卡车(车辆技术参数如表1所示)以60 km/h速度匀速通过桥梁,支座的法向刚度系数K0和法向阻尼系数C0分别为1.60×106kN/m和9.8×103kN·s/m。

表1 空间三轴车辆技术参数

表示方法》(GB/T 7031—1986)中功率谱密度,利用MATLAB进行Fourier逆变换得到了A、B、C、D等级桥面不平整度反演如图4所示。

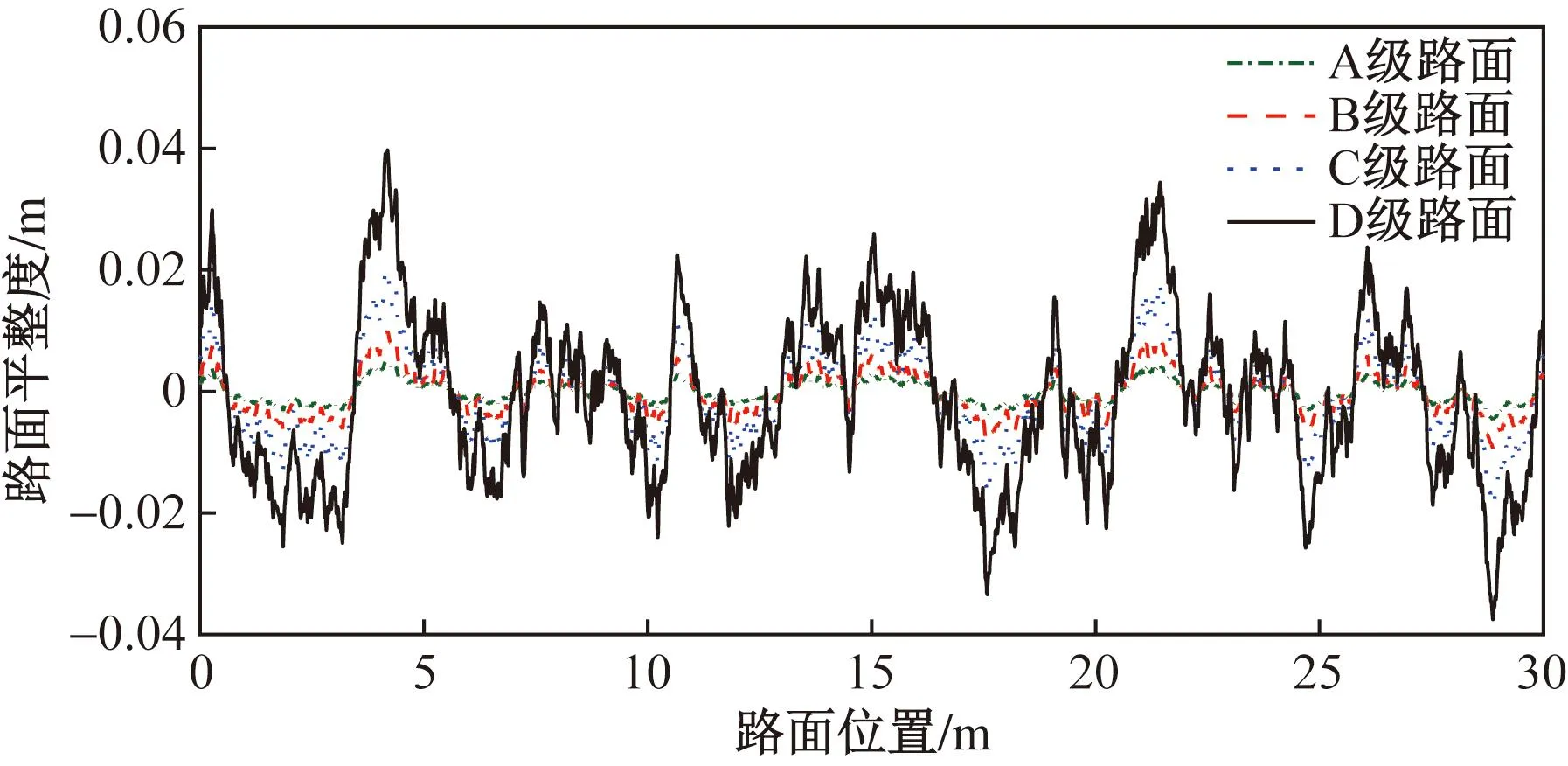
图4 路面不平整度反演

计算得到了桥面不平整度对桥梁动力响应的影响如图5～图7所示。

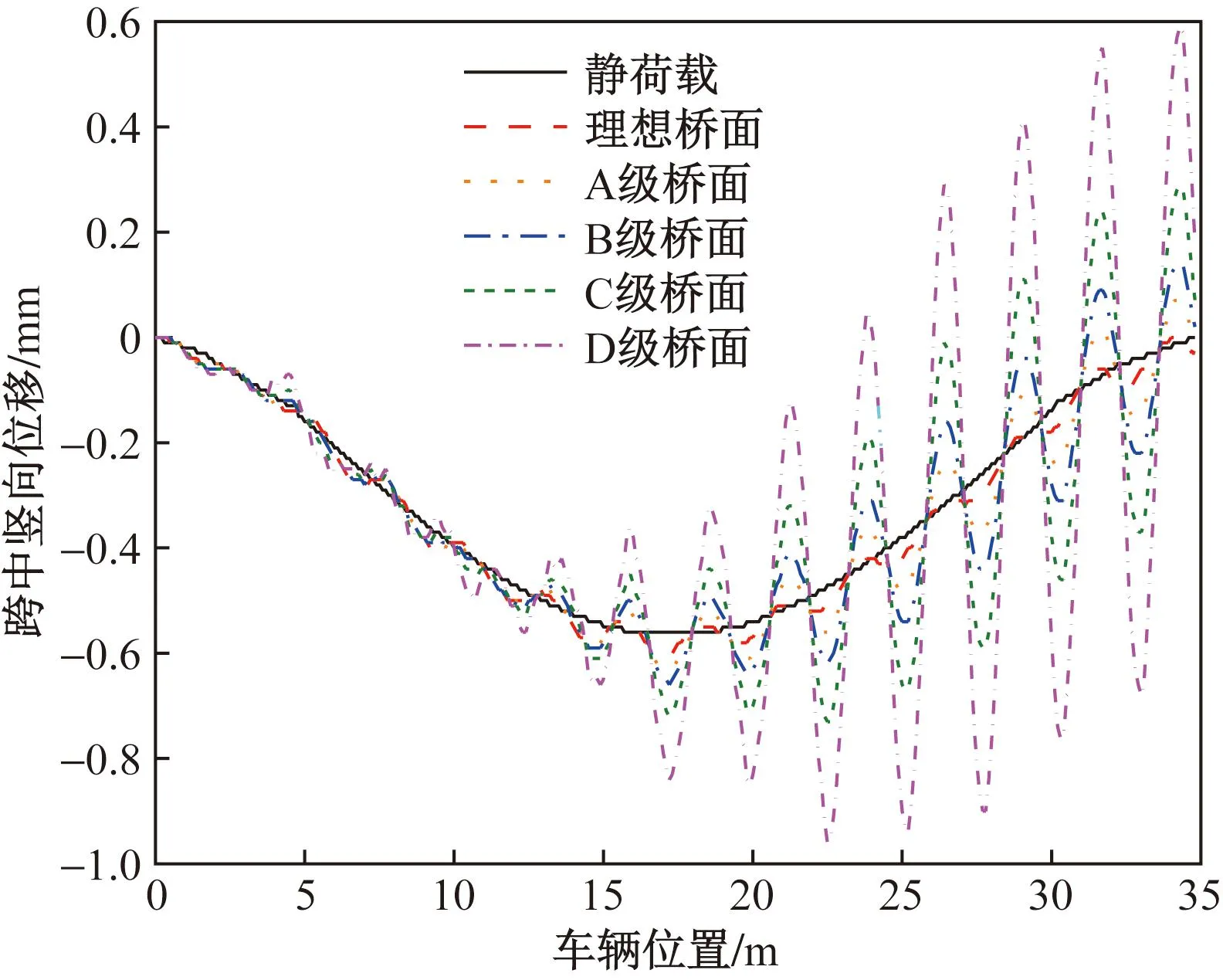
图5 不同等级桥面简支梁跨中竖向位移响应曲线

图5为跨中竖向位移响应曲线,车辆行驶在桥梁上,随着桥面状况变差,跨中的振动幅度越大,动力响应越激烈,而且由于车辆行驶速度较快,桥梁动力响应有明显的滞后现象。

图6和图7分别为1#支座和2#支座的竖向反力响应曲线,支座的动力响应随着桥面状况变差而增大,由于响应滞后,2#支座出现的瞬时反力比1#支座更大,图中曲线出现的三级阶梯为车辆的三个车轴进出桥梁瞬间所造成的支座反力突然增大或减小。

图6 不同等级桥面简支梁1#支座反力响应曲线

图7 不同等级桥面简支梁2#支座反力响应曲线

移动荷载动力冲击系数(impact factor,IM)采用国际常用的表达式定义:

(18)

式中:Rdyn、Rsta分别为移动荷载作用下的桥梁动力效应时间历程曲线上的最大动效应和最大静效应。

根据公式(18)计算得到不同等级桥面简支梁动力冲击系数IM如表2所示。跨中和支座的动力冲击系数IM均随着桥面等级下降单调增大如图8所示。与理想桥面相比,在A、B、C、D等级桥面下,跨中IM分别增大了76.1%、152.1%、328.2%、905.6%,1#支座IM分别增大了50.0%、183.3%、466.7%、1 016.7%,2#支座IM分别增大了71.4%、185.7%、728.6%、1 957.1%。分析结果表明,桥面的优劣程度对车-桥-支座耦合动力响应的影响非常大,桥面平整度越差,系统产生的动力响应越激烈。

表2 不同等级桥面简支梁动力冲击系数计算结果

图8 不同等级桥面下跨中IM变化曲线

3.2 支座刚度的影响

为了研究支座刚度大小的影响,引入比例因子α,设支座刚度系数为K=αK0(K0=1.60×106kN/m为初始刚度系数),α分别取值0.01、0.02、0.05、0.1、0.2、0.5、1.0、1.5、2.0。

分析工况:单辆三轴卡车(车辆技术参数如表1所示)以60 km/h速度匀速通过桥梁(理想等级桥面),支座阻尼系数C0为9.8×103kN·s/m。

分析得到不同支座刚度下,简支梁跨中竖向位移响应曲线如图9所示,支座反力响应曲线如图10所示,计算得到不同支座刚度下简支梁动力冲击系数如表3所示。从图9和表3可以看出随着支座刚度增大,跨中动力冲击系数不断减小,但是当α>1.0时,再继续增大支座刚度对减小跨中竖向动位移的贡献变得很小,与刚性支座下的挠度曲线非常接近。从图10和表3可以看出支座刚度变化对支座动力冲击系数的影响很小,支座反力动力冲击系数最大值为0.09。

表3 不同支座刚度简支梁动力冲击系数计算结果

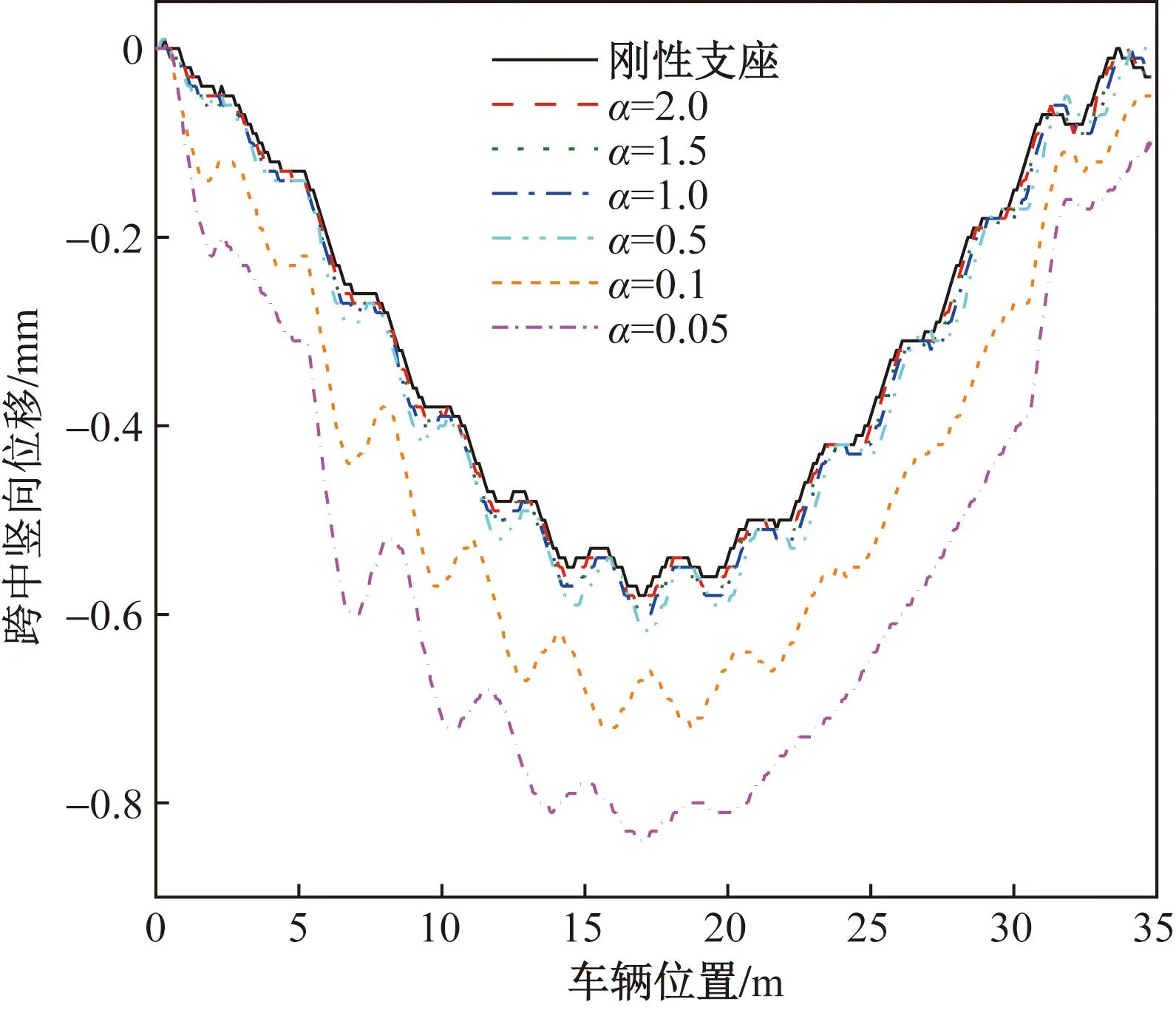
图9 不同支座刚度跨中竖向位移响应曲线

图10 不同支座刚度下支座竖向反力响应曲线

3.3 支座阻尼的影响

引入比例因子β,设支座刚度系数为C=βC0(C0=9.8×103kN·s/m为初始阻尼系数),β分别取值0.01、1.0、100.0。

分析工况:单辆三轴卡车(车辆技术参数如表4所示)以60 km/h速度匀速通过桥梁(理想等级桥面),支座刚度系数K0=1.60×106kN/m。

表4 不同支座阻尼简支梁最大瞬时加速度计算结果

分析得到不同支座阻尼下,简支梁跨中竖向加速度响应曲线如图11所示,支座加速度响应曲线和反力响应曲线如图12和图13所示,计算得到不同支座阻尼下简支梁最大瞬时加速度如表4所示。由图13可知不同支座阻尼情况下,各支座竖向反力变化规律基本一致。从图14可以看出增大支座阻尼对削弱简支梁加速度响应有明显的效果,随着支座阻尼增大,可以有效降低桥梁瞬时加速度的峰值。

图11 不同支座阻尼跨中竖向加速度响应曲线

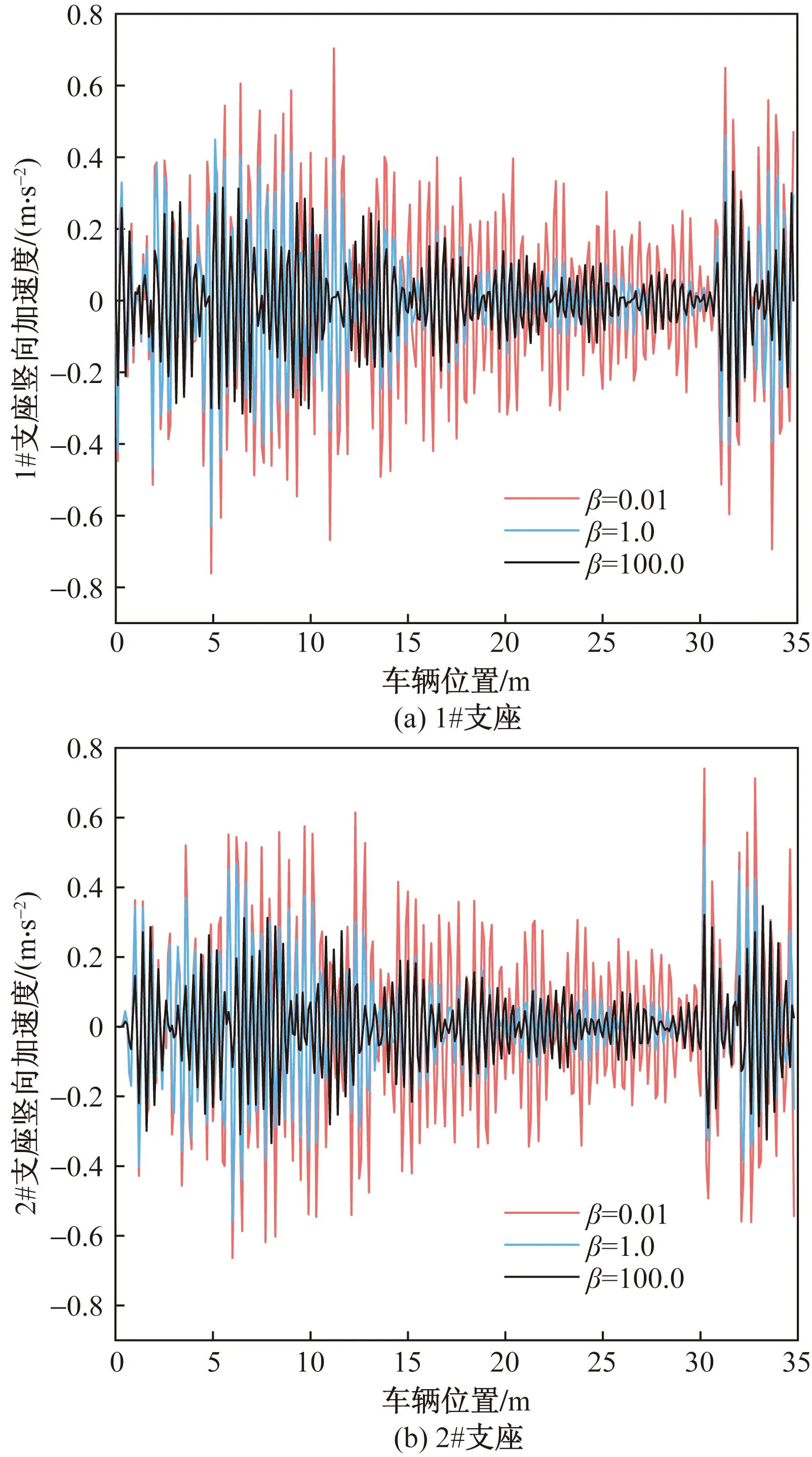
图12 不同支座阻尼下支座竖向加速度响应曲线

图13 不同支座阻尼下支座竖向反力响应曲线

图14 最大瞬时加速度变化曲线

4 结论

本文基于ANSYS中APDL语言,结合分离法与汽车动力学原理,分别建立车辆、桥梁和支座3个子系统的计算模型并通过位移协调关系和力的平衡关系进行车-桥-支座耦合,以公路桥梁常用的30 m预制简支箱梁为算例详尽分析了桥面不平整度、支座刚度和阻尼对车-桥-支座耦合动力响应的影响,得到以下结论。

(1)桥面不平整度是影响车-桥-支座耦合动力响应的一个非常重要的因素,桥面平整度越差,车辆行驶过程中振动越激烈,对桥梁结构产生的冲击作用力越大,激发桥梁振动越激烈。与理想桥面相比,在A、B、C、D等级桥面下,跨中IM分别增大了76.1%、152.1%、328.2%、905.6%,1#支座IM分别增大了50.0%、183.3%、466.7%、1 016.7%,2#支座IM分别增大71.4%、185.7%、728.6%、1 957.1%。

(2)支座刚度和阻尼对车-桥-支座耦合动力响应有较大影响。在一定范围内,增大支座刚度能有效降低桥梁跨中动力响应,减小跨中挠度IM,但当支座刚度增大到一定程度时,再继续增大支座刚度对减小跨中IM效果非常小;支座刚度变化对支座IM的影响很小;阻尼可以消耗结构振动产生的能量,增大支座阻尼对削弱桥梁加速度响应有明显的效果,随着支座阻尼增大,可以有效降低简支梁瞬时加速度的峰值。

(3)实际桥梁设计时,适当增大支座刚度和阻尼能有效削弱车-桥-支座耦合振动对桥梁的冲击作用,增强桥梁结构性能。