基于多Agent的锂电池主动均衡策略控制仿真研究
傅军栋 陈浩杰 孙翔 华天亮 刘深深 刘珺


摘要:【目的】针对锂电池的荷电状态均衡管理问题,提出一种基于多智能体的电池组荷电状态一致性均衡方案。【方法】首先,将多智能体控制策略引入电池管理的下垂控制中,实现了主动均衡电路拓扑下的自主均衡;其次,建立领航跟随者模型,利用参数已知的虚拟智能体使各个荷电状态不一致的电池的状态向其靠近,实现充放电模式下的荷电状态均衡;最后,对二阶多智能体荷电状态均衡控制策略进行仿真验证。【结果】实验结果表明,相比一阶均衡控制策略,自主均衡时间减少了43.02%,充电模式中均衡时间减少了16.13%,放电模式中均衡时间降低了32.90%。【结论】多智能体系统在电池的均衡管理中能够实现荷电状态的均衡,有效地降低了锂电池荷电状态到达一致性的收敛时间。
关键词:荷电状态;电池管理系统;主动均衡;均衡控制策略;多智能体
中图分类号:U279.5; TP311 文献标志码:A
本文引用格式:傅军栋,陈浩杰,孙 翔,等. 基于多Agent的锂电池主动均衡策略控制仿真研究[J]. 华东交通大学学报,2024,41(1):96-104.
Simulation on Active Equalization Strategy Control for
Multi-Agent Lithium Battery
Fu Jundong, Chen Haojie, Sun Xiang, Hua Tianliang, Liu Shenshen, Liu Jun
(School of Electrical and Automation Engineering, East China Jiaotong University, Nanchang 330013, China)
Abstract: 【Objective】Aiming at the problem of charging state balance management of lithium battery, a multi-Agent based battery pack consistent charging state balance scheme was proposed. 【Method】Firstly, the multi-Agent control strategy is introduced into the sagging control of battery management, and the autonomous balancing under the active balancing circuit topology was realized. Secondly, the lead follower model is established, and the virtual agents with known parameters are used to make the state of each battery with inconsistent charging state close to it, so as to achieve the charging state balance in charge-discharge mode. Finally, simulation verification of the two-order multi-Agent state load balancing control strategy is carried out. 【Result】The experimental results show that, compared with the first-order balancing control strategy, the autonomous balancing time is reduced by 43.02%, the balancing time in charging mode is reduced by 16.13%, and the balancing time in discharge mode is reduced by 32.90%. 【Conclusion】The multi-Agent system can achieve the balance of SOC in battery balancing management, effectively reducing the convergence time of SOC reaching the consistency of lithium battery.
Key words: charging state; battery management system; active equilibrium; equilibrium control strategy; multi-Agent
Citation format:FU J D, CHEN H J, SUN X, et al. Simulation on active equalization strategy control for multi-Agent lithium battery[J]. Journal of East China Jiaotong University, 2024, 41(1): 96-104.
【研究意義】单节锂电池的容量或功率并不能满足中大型负载,因此在运用上多表现为串并联而成的电池组来满足负载的用电需求。受限于制作工艺,电池存在个体性能差异,在使用过程中,电池内部环境存在放电不均匀的情况。如果在充、放电过程中没有很好地解决异常使用的问题,随着使用时间的增加,不同电池之间的性能差异将扩大,造成电池组循环寿命和放电效率急剧下降[1]。电池管理系统(battery management system, BMS)中的电池均衡管理模块很重要[2],可以有效降低电池组内部的荷电状态(state of charge, SOC)不一致问题,提高循环使用寿命,对于实现电池的安全、健康运行具有重要意义[3]。
【研究进展】在均衡控制策略的变量选择上,使用SOC比电压作为均衡准则能更有效利用动力电池组的容量[4]。刘胜崇等[5]采用模糊理论以SOC作为变量,解决了过度充放电造成的荷电状态不均衡导致的输出电压波动问题。虽然SOC作为均衡参数能保证控制精度,但是SOC值的预测存在估算精度问题[6]。传统均衡控制策略中,下垂控制及其变式作为多储能系统中的SOC均衡控制方案得到了最为广泛的应用。Olivares等[7]对基于下垂控制、模型预测控制和多智能体系统的控制策略进行了概述,并将控制策略分为三个等级,认为其是未来控制的趋势。吕冬翔等[8]针对连续系统模型和离散系统模型进行研究,并通过理论分析说明分布式系统在能源均衡控制方面的可行性。【关键问题】将均衡控制策略和系统相结合是未来的研究方向,研究一种能够实现电池能量在线、快速均衡的均衡控制管理是保证电池组长期高效、健康工作的关键。
【创新特色】本文将均衡拓扑和均衡策略通过电源管理系统进行结合,提出一种基于LC-L的电池组均衡方法,将多智能体控制策略引入BMS的下垂控制管理中。设计了基于多智能体的动态平均一致性的荷电状态均衡控制算法并进行了验证。在系统完成均衡的基础上,相比传统的一阶多智能体均衡控制策略,通过领航者模式,提出了二阶多智能体一致性均衡策略。在充、放电过程中使SOC初始值不同的电池实现荷电状态一致,缩短了电池组达到荷电状态平衡的时间。
1 均衡控制管理
均衡管理技术极为重要,现有的电池均衡方法和策略均未能同时兼顾均衡效率、速度、成本和系统复杂度。从整体上看,均衡管理的目的是对电池组内单体电池的不一致性进行均衡,使其保持充放电的动态平衡。不同的电路拓扑结构和控制策略有不同的特点,将二者进行结合共同研究均衡管理。将SOC作为均衡一致性参考变量,减少均衡损耗、提高均衡速度和降低系统结构的复杂度对电池组进行主动均衡能有效提高均衡效率。
1.1 电池管理系统
BMS是电池系统的核心组成部分[9],主要作用是监测电池组电压、电流和温度等重要参数,在数据分析后获取电池组的荷电状态和功率状态,通过控制电路中的电力电子器件保障系统安全运行。
1.2 下垂控制
在均衡电路中,电池的荷电状态通常以安时积分法进行估算,表达式如下所示
式中:[SOC0]为电源的初始容量;[iB]为放电电流;[QN]为电池额定容量;[K]为与充放电相关的影响系数,包含温度影响下的系数[K1],充放电转换因子[K2],电源老化周期系数[K3],充放电倍率影响系数[K4]。
输出功率为[PB],[uB]为端电压,充放电倍率[C],满足
电压下垂控制表达式为
式中:[udc]为直流母线电压;[Udc]为直流母线电压参考值;[k]为下垂系数,联立式(1)和式(3),得到
对式(6)两端求导,因为端电压的变化较小,视为常数,可得
代入式(4)和式(5),有
因此,可以通过电池的充放电功率实现对SOC变化速率的动态调节,电池的功率变化越小,SOC的变化速度越慢。而下垂控制中的电压大都控制在额定电压附近,所以储能荷电状态均衡及其变化速率主要受下垂系数k和充放电相关的影响系数K控制。
1.3 荷电状态估计
电池荷电状态作为判断电池使用周期的一个重要指标,是电池管理系统进行电池管理的主要依据。近年来,拓展卡尔曼滤波算法(extended Kalman filter, EKF)在电池的SOC估算中应用十分频繁。
图1为二阶RC戴维南等效电路。E为锂电池电动势,[R1]和[R2]为极化内阻,[R3]为欧姆电阻,[C1]和[C2]为极化电容,负载电压为V,[I1]和[I2]为支路电流,I为干路总电流。
将等效电路模型带入EKF模型表达式中,求解出关于等效电池模型的狀态空间矩阵模型
1.4 均衡电路拓扑
单纯的电感和电容均衡电路都有缺点[10-11],目前均衡电路大都是电感-电容复合型电路。本文在基于LC-L储能的串联电池组主动均衡拓扑结构上加入均衡控制策略,多电池系统的均衡电路拓扑结构如下所示。
在获得各个电池的荷电状态值后,电路拓扑将高SOC的电池单体的能量转移到电路中基础储能元件,通过储能器件提供续流回路,再将电能转移给SOC较低的电池单体,在电感电容谐振电路实现能量转移的同时,利用缓冲电路减小回路电流,改善阶梯效应,使得各个电池的荷电状态保持一致,为能量的可靠传递提供了保障。
2 多智能体模型
2.1 智能体荷电状态均衡
在多电池组成的多智能体系统中,每个智能体获得其他智能体的相关信息,通过SOC平均一致性动态算法更新自身信息并向拓扑图中相邻智能体发送自身的荷电状态估计值。
以图论的观点通过拉普拉斯来实现多智能体系统的设计[12],在多智能体系统中,智能体信息交流可用图[G=A,E,V]表示,图中N个非空点集合表示为[V=v1,v2,v3,…,vn],E表示智能体的集合边缘,邻接矩阵记作[A],且[An×n=[aij]],度矩阵记作[D],且[D=diag{d1,d2,…,dn}],且[dj=j=1,j≠inaij]。图G的Laplacian矩阵记为L,且[L=D-A]。智能体组成的非线性系统,动力学模型可为
式中:f为非线性函数;[xi(t)]为智能体的状态;[ui(t)]为系统地控制输入;[vi(t)]为速度信息,在多智能体系统中将[vi(t)]作为系统的控制输入,其值与电池放电倍率C有关。
在智能体系统的均衡模式下[13],首先将每一节电池视作一个智能体,单位时间内的电流动态一致性更新公式如下所示
式中:[ipj]为输出电流和电池容量的比值,[ipj]为智能体i所接收到智能体j的电流估计值,[ρ1]为单位时间内电流状态的动态平衡系数,[Ni]为无向图中与节点i相连的節点的集合,基于前时间序列数据预测电池i当前的荷电状态[SOCi(t)],智能体i接收来自智能体j的荷电状态预测值[SOCj(τ)],同时将自身当前预测值[SOCi(t)]发送给j,通过SOC的动态平均一致性算法更新自身信息,荷电状态预测值在多智能体一致性算法中的更新模式如下
式中:[ρ2]为单位时间内荷电状态动态平衡系数,当[t→∞]时[SOCi-][SOCj=0],即所有智能体的荷电状态最后都趋于相同的值。
变换微分时域形式为
对式(14)进行拉氏变换,根据对应的智能体i和j的拓扑图引入Laplacian矩阵,向量表达式为
式中:[s]为拉普拉斯算子;[SOC]为[SOCpi]的拉氏变换形态,表示智能体的平均值向量;[SOCX=[SOC1,][SOC2,…,SOCN]T]为智能体的荷电状态向量。电池的平均估计向量和电池荷电状态向量相等,即[SOC(0)=SOCX(0)],最终得到估计值[SOC]和测量值[SOC]
2.2 二阶智能体模型
考虑到二阶模型可以用来描述现实中更复杂的过程,研究重点从一阶系统转向二阶系统的一致性问题。拓扑下有未知动态的非线性多智能体系统有限时间一致性在完整的多智能系统中跟随者和领航者也应当满足完整的约束条件,下式是二阶多智能体系统里的一致性模型
与一阶模型相同,[xi(t)]仍是表示智能体的状态。二阶模型中[ui(t)]表示智能体的控制输入信息,即放电倍率对时间的求导[iB],可直接控制被控对象的控制输入记作[ai]。[α,][β]分别为该系统的耦合强度,智能体的控制输入信息更新公式为
基于LaSalle不变性原理[14],在事件驱动控制配置下,网络拓扑结构中包含全局可达节点时,且满足入度平衡,多智能体系统可以渐进实现分组一致。对二阶多智能体控制系统,结合式(12)和式(13),得到多能体系统的荷电状态更新公式为
因为[vi(t)]与充放电倍率C相关,在二阶控制策略中,均衡系统的控制输入的公式满足
所以在二阶智能体的均衡控制模式下,系统通过单体的状态信息和改变放电倍率信息的二阶积分器模型改变[iB]的变化范围从而降低系统到达均衡的时间。
2.3 领航者模型
但在实际应用过程中,锂电池的均衡管理不但要考虑到系统的自主均衡,还应考虑到充放电模式下的SOC均衡。在多智能体的基础上结合跟随领航者模型能在充放电时对荷电状态进行均衡[15],均衡系统跟随领航者模型的信息交流如图3所示。
在整个系统中根据智能体最后需要到达的状态设置一个虚拟的领航者,其余的成员为跟随者。虚拟领航者的状态信息被智能体获得,则模型的信息传递网络可以描述为[G=(Vn, E)],[Vn]代表各个智能体的顶点;E?[Vn]×[Vn],代表智能体之间的连接边。智能体i和它的邻接智能体j之间的信息交流用一个有向边表示。
本文把每个电池看作一个智能体,为了克服下垂控制对电压的影响,每个智能体使用本地信息和它的邻接智能体信息来更新本地的平均电压估计值。
每个智能体仅需要和邻接智能体进行信息交流,多智能体交流网络复杂程度大大降低。穿过智能体的平均电压(非特定电压)被用作末端控制,调节全局电压设定点。多智能体二级控制可表示为
式中:[uti(t)]为智能体i的本地估计平均电压;[uti(t)]为智能体i的输出母线电压;[β]为平均电压一致收益;[Ni]为智能体i的邻接智能体的数目。在此控制协议下,最终实现
根据式(18)可知,当智能体i的本地估计平均电压大于其邻接智能体的平均电压时,增加智能体i的邻接智能体的数目[Ni],使得[uti(t)]减小,可以缩小式(22)的电压均衡时间t。
由于模型中领航者参数值已知,并不断将信息传递给跟随者,跟随者向领航者的状态不断运动靠拢,最终就达成整个系统状态一致[16]。跟随领航者模型的方式最大优点是直观、易于理解,但是缺点是在领航者被干扰或是参数不明的情况下会对整个系统的运行造成影响。
3 仿真模拟
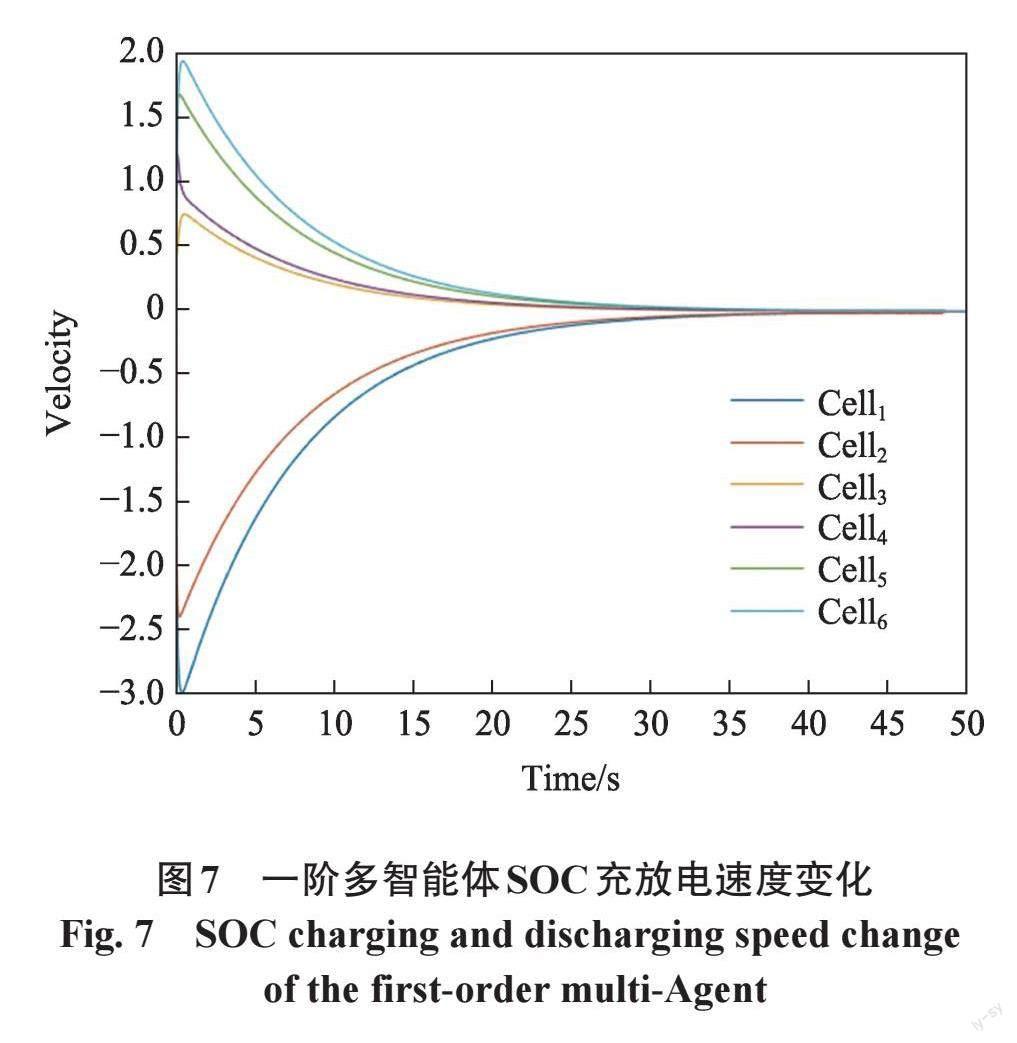
图4是均衡控制管理系统中的均衡流程图,为验证本文提出的基于多智能体的荷电状态均衡控制策略的有效性,在Matlab/Simulink仿真平台上搭建了电路仿真模型,以荷电状态作为参考变量,使其保持充放电的动态平衡。该仿真系统包含由6个电池构成的电池包,为了使电池储能系统的荷电状态达到平衡,根据系统中的各个电池的SOC调节每个电源的输出有功功率,通过对PI控制器的不断修正解决电池单元容量和SOC不一致的问题,最后通过电压电流双闭环控制器生成脉冲占空比,并经过PWM (pulse width modulation) 生成器将占空比调制成接受的脉冲信号。信息传递网络中将对应电池相互连接从而构成一种链式结构,且每个电池的初始容量不完全相同,在系统的自主均衡中,不考虑领航者模型。由6节电池组成的多智能体系统,其使用的无向连接图如上图5所示。在均衡开始时,设定6个电池的初始荷电状态[SOC(0)]分别为[78.61%,73.61%,49.23%,47.98%,42.22%,35.69%],动态一致性参数[ρ1=1.1, ft,xi(t)=0.01×xi(t)],时间周期的步长[t=][0.10 s]。为了使智能体系统的SOC达到平衡,通过外电路的均衡拓扑结构调节每个电源的有功功率。图6为多智能体间荷电状态均衡控制SOC均衡轨迹变化图。图7为SOC均衡下功率控制的速度,其为荷电状态与时间的比值,正值代表充电下的SOC增长速度,负值为放电下的SOC减少速度。
由图7可知,随着每个电池的自主均衡控制功率的速率降低,荷电状态均衡的速率在加快,电池之间的荷电状态差值慢慢缩小。初始6个智能体间的[SOC(0)]平均值为54.55%,在均衡控制t=43.00 s时,6个智能体的荷电状态值逐渐收敛并最终在54.44%处达成自主均衡。对充放电模式下的均衡,本文设计由一个参数已知的虚拟领航者作为主智能体和N个跟随者构成的多智能体系统,图8为跟随领航者控制模型的无向网络拓扑图。
以充电模式中的荷电状态均衡为例,建立由“1+6”节锂电池组成多智能体系统。系统中最后电池组内电池都需要到达的SOC值为80%,则式中虚拟领航者的值设为80%,不需要接收其他节点中智能体的信息。剩余6节全为跟随者,以下垂控制法对智能体实施均衡,图9是充电模式下的SOC均衡趋势变化图,图10是放电模式下SOC均衡趋势变化图。
结果显示,一阶多智能体均衡系统中,将荷电状态80%的虚拟智能体设置为领航者后,在充电模式下,6个初始荷电状态不一致的智能体跟随领航者进行充电均衡。当充电时间为t=39.75 s时,到达平衡;放电模式下,当放电时间为t=32.50 s时,实现了电池组放电下荷电状态的均衡。图11为自主均衡模式下二阶SOC均衡图,
由图可知,二阶下的自主均衡在时间24.50 s的时候SOC达成一致。设置初始充电功率速度为[v=[0.5,0,0,0,0,0,0]],根据提供的数据,采样时间t=0.01 s,同时选取二阶加权参数[ai]为4.5。对虚拟领航者设置SOC充电恒定速度[v0]为0.5,不同于充电模式,初始放电功率速度[v=[0,0,0,0,0,0,0]],对虚拟领航者设置荷电状态放电控制速度[v0]为0。图12为充电模式下二阶跟随领航者SOC均衡图,图13为放电模式下二阶跟随领航者SOC均衡图,
结果显示,充电模式中设置荷电状态75%的虚拟智能体为领航者后,6个跟随智能体的荷电状态逐渐趋同于领航者。相比一阶智能体均衡系统,二阶系统在锂电池组实现均衡时,时间t=33.34 s,均衡时间大大提前。到达平衡时,6节电池的SOC均为82.80%,实现了多电池充电下SOC的均衡,荷电状态的最大差异从42.92%成功降至0。
放电模式中设置荷电状态35.69%的虚拟智能体为领航者后,6个跟随智能体的荷电状态逐渐趋同于领航者。二阶系统在电池放电模式實现均衡时,时间t=21.80 s,实现了多电池充电下SOC的均衡。表1为同一均衡电路拓扑结构下不同控制策略的均衡结果。
4 结论
本文对均衡电路拓扑下基于多智能体均衡一致性方法对锂电池荷电状态均衡管理进行探讨,将均衡控制策略与均衡电路拓扑结合,并进行均衡控制仿真验证。
1)实现多智能体下的自主均衡控制后,引入领航跟随者模型,实现在充放电模式下的SOC均衡控制,其均衡时间分别为39.75 s和32.5 s。
2)在一阶控制策略的基础上进一步使用二阶均衡控制策略。与一阶控制策略相比,二阶控制策略自主均衡时间减少了43.02%,充电模式中均衡时间减少了16.13%,放电模式中均衡时间降低了32.90%,其SOC均衡曲线更加平滑,减少了锂电池SOC一致性收敛时间,保证电池组长期高效、健康工作。
参考文献:
[1] HUA Y, ZHOU S, CUI H, et al. A comprehensive review on inconsistency and equalization technology of lithium-ion battery for electric vehicles[J]. International Journal of Energy Research, 2020, 44(14): 11059-11087.
[2] 张婕, 曾国辉, 赵晋斌, 等. 基于改进冒泡排序的模块化多电平换流器电容电压均衡策略[J]. 电力系统保护与控制, 2020, 48(6): 92-99.
ZHANG J, ZENG G H, ZHAO J B, et al. Modular multilevel converter capacitor voltage balancing strategy based on improved bubble sorting[J]. Power System Protection and Control, 2020, 48(6): 92-99.
[3] GHAEMINEZHAD N, OUYANG Q, HU X, et al. Active cell equalization topologies analysis for battery packs: A systematic review[J]. IEEE Transactions on Power Electronics, 2021, 36(8): 9119-9135.
[4] ZHANG X, YAN G. Estimating SOC and SOH of lithium battery based on nano material[J]. Ferroelectrics, 2021, 580(1): 112-128.
[5] 刘胜崇, 帕孜来·马合木提, 葛震君. 基于模糊控制的蓄电池系统储能单元SOC均衡方法[J]. 现代电子技术, 2020, 43(24): 135-139.
LIU S C, PAZILAI M, GE Z J. Fuzzy control based SOC equalization method for battery energy storage unit[J]. Modern Electronic Technique, 2020, 43(24): 135-139.
[6] NASERI F, SCHALTZ E, STROE D I, et al. An enhanced equivalent circuit model with real-time parameter identification for battery state-of-charge estimation[J]. IEEE Transactions on Industrial Electronics, 2022, 69(4): 3743-3751.
[7] OLIVARES D E, MEHRIZI-SANI A, ETEMADI A H, et al. Trends in microgrid control[J]. IEEE Transactions on Smart Grid, 2014, 5(4): 1905-1919.
[8] 吕冬翔, 张志成, 朱立宏, 等. 基于多智能体的太阳能无人机能源控制研究[J]. 控制与决策, 2023, 38(2): 372-378.
LYU D X, ZHANG Z C, ZHU L H, et al. Multi-agent based energy control for solar unmanned aerial vehicles[J]. Control and Decision Making, 2023, 38(2): 372-378.
[9] GUERRERO J M, VASQUEZ J C , MATAS J, et al. Hierarchical control of droop-controlled AC and DC microgrids—a general approach toward standardization[J]. IEEE Transactions on Industrial Electronics, 2011, 58(1): 158-172.
[10] MORSTYN T, SAVKIN A, HREDZAK B, et al. Multi-agent sliding mode control for state of charge balancing between battery energy storage systems distributed in a DC Microgrid[J]. IEEE Transactions on Smart Grid, 2017: 1-7.
[11] 傅軍栋, 陈康, 黄扬海. 基于Agent的变电站通信研究[J].华东交通大学学报, 2020, 37(3): 117-126.
FU J D, CHEN K, HUANG Y H. Research on substation communication based on agent[J]. Journal of East China Jiaotong University, 2020, 37(3): 117-126.
[12] 张赟, 王琛, 王毅, 等. 基于自适应下垂控制的直流微电网多储能SOC动态均衡策略[J]. 华北电力大学学报(自然科学版), 2020, 47(5): 21-29.
ZHANG Y, WANG C, WANG Y, et al. SOC dynamic balancing strategy for multi-energy storage based on adaptive droop control in DC microgrid[J]. Journal of North China Electric Power University (Natural Science Edition), 2020, 47(5): 21-29.
[13] GOZDUR R, PRZERYWACZ T, BOGDA?SKI D. Low power modular battery management system with a wireless communication interface[J]. Energies, 2021, 14.
[14] 李斌, 郭亮, 刘双华, 等. 无线抬动监测装置电源管理关键技术研究[J]. 长江科学院院报, 2020, 37(3): 150-154.
LI B, GUO L, LIU S H , et al. Key technologies for managing the power supply of wireless uplift monitoring device[J]. Journal of Changjiang River Scientific Research Institute, 2020, 37(3): 150-154.
[15] YANG S, MA S, GUAN S, et al. 2021 IEEE 4th International Electrical and Energy Conference (CIEEC),May 28-30, 2021[C].Wuhan:IEEE,2021.
[16] CHEN H, LI S, WU S. Hybrid energy storage module in photovoltaic power generation system for brushless DC motor operation[J]. Sensors and Materials. 2022, 34(2): 871-884.
第一作者:傅军栋(1972—),男,副教授,研究方向为电力系统、智能建筑。E-mail:8755915@qq.com。

