基于自抗扰解耦的电力电子牵引变压器整流级直接功率控制

张辉 宋平岗 连加巍 刘德松 宋泽昆

摘要：【目的】为改善电力电子牵引变压器（PETT）整流级在传统dq电流解耦双闭环控制下抗干扰能力差、对参数变化敏感、谐波含量高等问题。【方法】通过对直接功率控制（DPC）的解耦方式进行改进，提出了一種无需系统角频率和电感参数基于自抗扰控制（ADRC）的功率解耦控制器。最后，在Matlab/Simulink中搭建模型进行不同工况的仿真分析。【结果】仿真结果表明新型控制策略较传统控制策略网侧电流THD值减少5.38%，等效电感突变时电压跌落值减少48 V，电压频率偏移时电压跌落值减少14 V，新型控制策略在负载突变和负载不平衡工况下具有较好的平衡控制效果。【结论】该控制器通过解耦实现了有功功率和无功功率精确且独立的控制。仿真结果验证了所提控制策略的合理性与有效性。

关键词：单相级联H桥整流器；电力电子牵引变压器；自抗扰解耦；电容电压平衡；直接功率控制

中图分类号：U224；TM461 文献标志码：A

本文引用格式：张辉，宋平岗，连加巍，等. 基于自抗扰解耦的电力电子牵引变压器整流级直接功率控制[J]. 华东交通大学学报，2024，41（1）：54-60.

Improved Direct Power Control of Rectifier Stage of Power

Electronic Traction Transformer

Zhang Hui， Song Pinggang， Lian Jiawei， Liu Desong， Song Zekun

（School of Electrical and Automation Engineering， East China Jiaotong University， Nanchang 330000， China）

Abstract： 【Objective】In order to improve the poor anti-interference ability， sensitivity to parameter changes， and high harmonic content of the PETT rectifier stage under traditional dq current decoupling double closed-loop control in order to improve the problem. 【Method】By improving the decoupling method of DPC， a power decoupling controller based on ADRC was proposed， without requiring system angular frequency and inductance parameters. Finally， a model was built in Matlab/Simulink for simulation analysis under different operating conditions.【Result】The simulation results showed that the new control strategy reduced the THD value of the grid side current by 5.38% compared to the traditional control strategy， reduced the voltage drop value by 48 V when the equivalent induct-ance suddenly changed， and reduced the voltage drop value by 14 V when the voltage frequency shifted. 【Conclusion】This controller achieves precise and independent control of active and reactive power through decoupling. The new control strategy has good balance control effect under load sudden change and load im-balance conditions. The simulation results verify the rationality and effectiveness of the proposed control strategy.

Key words： single phase cascade H-bridge rectifier; power electronic traction transformer; active disturbance rejection decoupling; capacitor voltage balance; direct power control

Citation format：ZHANG H， SONG P G， LIAN J W， et al. Improved direct power control of rectifier stage of power electronic traction transformer[J]. Journal of East China Jiaotong University，2024，41（1）：54-60.

【研究意义】自抗扰控制系统的主要组成部分包括：跟踪微分器（TD）、扩张状态观测器（ESO）、非线性误差反馈控制率（SEF）[1]。其优点在于通过误差来消除误差，将系统中的不确定因素视为“未知扰动”，并补偿扰动对系统的影响，可将不确定的，复杂的系统简单化。基于上述优点，自抗扰控制在本研究中作为一种新型的控制方法被运用到电力电子牵引变压器整流级，并取得了较好的控制效果。

【研究现状】自抗扰控制理论自提出以来，距今已有20多年的历史，后续又有众多学者对其进行了深入的研究。如高志强在ADRC的基础上通过引入频率尺度的概念提出了线性自抗扰控制（line active disturbance rejection control， LADRC）的概念，通过引入观测器带宽、控制器带宽和扰动补偿3个参数简化了ADRC的参数设计方法[2-3]。陈增强对线性自抗扰的理论及其实际应用进行了综述[4]。后续众多学者的相关研究极大地推动了自抗扰理论的飞速发展和自抗扰技术在生产实践中的应用。基于自抗扰的解耦技术作为一种新型的解耦控制方法，不需要详细的模型，就能够解决系统的耦合问题，已经在诸多领域得到应用。于雁南等[5]将自抗扰解耦应用到级联H桥静止无功发生器中，增强了系统的鲁棒性和抗干扰能力。付文强等[6]提出将自抗扰解耦应用到PMSM调速系统，提高了系统的调速精度。张先勇等[7]将自抗扰解耦应用于风力发电功率系统，提高了风能的捕获效率。

【创新特色】虽然自抗扰解耦已经应用于诸多领域，然而文中所提将自抗扰解耦与直接功率控制结合的策略在电力电子牵引变压器整流级尚未有文献对其进行介绍。因此，本文在直接功率控制的基础上，对电力电子牵引变压器前级系统中耦合的有功功率和无功功率采取自抗扰解耦控制策略。

【关键问题】本文所提的自抗擾解耦控制策略成功地解决了电力电子牵引变压器整流级在传统控制策略下抗干扰能力差、对参数变化敏感、谐波含量高等问题。

1 整流级控制策略

1.1 单相级联H桥整流器数学模型

电力电子牵引变压器前级系统常见的拓扑结构有级联H桥型、多电平钳位型和模块化多电平型。其中，级联H桥型拓扑结构以其模块化程度高、调制算法简单、易实现冗余等诸多优点得到了广泛的应用。文章选择三级联H桥进行研究，其结构如图1所示。图1中uab为交流侧输入电压；us为网侧电压；Ti1，Ti2，Ti3，Ti4（i=1，2，3）为H桥开关器件； uC1，uC2，uC3分别为直流侧等效电容C1，C2，C3的电压；Ls为等效电感；is为网侧电流；id与iR分别为直流侧电流和直流侧负载电流；Rs为等效电阻；R1，R2，R3为各H桥等效电阻。

在本课题组前期研究的基础上[8]可得，在理想工作状态下级联H桥与单相全桥型PWM整流器可等效分析。其等效拓扑结构如图2所示。

根据基尔霍夫电压定律可得交直流两侧的数学模型为

1.2 级联H桥整流器的直接功率控制原理

考虑到文中所提电力电子牵引变压器为单相供电方式，在自由度单一的情况下，不能直接进行dq坐标变换，因此采用二阶广义积分SOGI模块构造虚拟正交分量[9]，则整流器交直流两侧数学方程式（1）在αβ坐标系下可以表示为

式中：网侧电压在αβ轴的分量为

式中：Un为网侧电压的幅值；w为工频频率。

单相系统中有功和无功功率在αβ坐标系下可以表示为

对式（4）进行求导得

将式（3）进行求导并联立式（2）与式（5）可得

其中，fp和fq为

进一步整理得

由式（8）可知，其功率模型是一个多变量、强耦合的非线性系统。

2 自抗扰解耦控制

2.1 自抗扰解耦控制策略

在设计自抗扰控制器之前，需先对式（8）中的耦合项进行解耦设计。为实现系统的精确解耦，本文采用静态解耦法实现对p和q的解耦，通过引入虚拟控制量将系统分解为单输入单输出的形式，大大降低了复杂度和运算量。其结果如式（9）所示[t=t1，t2T=（p，q）Tu=u1，u2T=fp，fqTU=Du=U1，U2Tf=f1f2=-RsLsp-wq-RsLsq+wpD=1Ls001LsD-1=Ls00Ls] （9）

式中：D为可逆矩阵；f为动态耦合部分；U为静态耦合部分。可将系统方程变换为

式（10）中的U是引入的虚拟控制量，从式中可以看出系统转换成了单输入单输出的形式，输出的有功功率p和无功功率q分别只与U1，U2有关，故系统的有功功率和无功功率通过虚拟控制量实现了完全解耦[6]。

式中f为系统的总扰动，由文献[5]可知，只要被控制量p，q的期望输入信号能够被测量，在虚拟控制量和p，q之间就可以设计两个自抗扰控制器，使p，q跟踪到期望输入信号p*和q*，从而达到解耦的目的。控制过程如图3所示。

由图3可知，利用自抗扰控制进行解耦，只需要考虑系统的静态耦合部分。

2.2 LADRC工作原理

LADRC的主要构成部分为线性扩张状态观测器（LESO）和线性误差反馈控制率（LSEF）。

2.2.1 LESO原理

对于一阶系统可以表示为如下形式

式中：σ为影响系统输出的扰动；b为控制器增益。为简化LESO的设计，可将式（11）改写为如下形式

选取新的状态变量，令[x1=y，x2=δ]，则式（12）可扩展为如式（13）所示的新的状态

采用龙贝格状态观测器理论设计状态观测器，状态方程如下

式中：z1，z2为LESO中x1，x2的观测值；λ1，λ2为观测器增益。

2.2.2 LSEF原理

假定LESO观测出的z2能够精确跟踪状态变量x2的值，则LADRC的控制率为

式中：b0为补偿因子，为b的估计值；此时可将系统简化，简化后的LSEF为

式中：x*为给定参考值；K为比例系数；u0为误差反馈量。系统传函可以表示为

将K配置到控制器极点，即[K=wc]；wc为控制器的带宽。线性自抗扰控制器的框图将在控制器的设计部分给出。

2.3 自抗扰解耦控制器的设计

因有功功率和无功功率解耦方式相同，文章选择以有功功率为例进行分析。

2.3.1 跟踪微分器的设计（TD）

为了减少起始误差，在设计LADRC之前先设计一个跟踪微分器进行过渡。如式（18）所示

式中：p*为期望输入信号；h为速度跟踪因子；vp为p*的跟踪信号。

2.3.2 线性扩张状态观测器的设计（LESO）

以式（8）中的有功功率为例[10]

令[-RsLsp-wq=δ]，[1Ls=b]。则可将式（19）改写为如下形式

令[x1=p]，[x2=δ]，将式（20）改写为一个新的状态方程

将式（21）进一步转换可得新的状态方程，如式（22）所示

可变换为

令[C=-λ11-λ20]，对于参数λ1，λ2可根据C的特征根求得

从式（24）中可求得[λ1=2w0]，[λ2=w02]，式中w0为观测器的带宽。

2.3.3 线性误差反馈控制率的设计（LSEF）

由2.2.2节中LSEF的原理得线性误差反馈控制率的模型如下

经此设计系统传函可表示为如式（17）所示。

根据以上分析得到控制器結构如图4所示。首先TD用于安排过渡过程，vp为期望输入p*的跟踪信号，此过程降低了起始误差；LESO通过z1估计系统状态变量vp；LSEF通过期望值vp与z1的差估计出误差反馈控制量u0；利用补偿因子b0，反馈控制量u0与观测值z2得最终的控制量u[5]。

3 电容电压平衡控制

电容电压是否平衡直接影响着电力电子牵引变压器的稳定运行。输出电压不平衡会造成系统效果差，严重时造成电容击穿，系统崩溃。因此，选择合适的电容电压平衡控制策略对电力电子牵引变压器的稳定运行至关重要。文章选择的电容电压平衡控制策略来自袁义生等[11]的研究。其基本控制过程为：每个H桥输出的电容电压与H桥输出电压的平均值U*做差，做差后的结果经过PI控制与调制信号Uε相乘得补偿量，补偿量μ1，μ2，μ3分别与调制信号Uε相加得H桥的调制信号d1，d2，d3。其控制框图如图5所示。

4 仿真分析

为证明文章所提控制策略的合理性，在simulink中搭建三级联H桥整流器模型进行仿真分析。模型参数选择如下：网侧电压311 V，频率50 Hz，直流侧电阻100 Ω，滤波电感5 mH，交流侧等效电阻0.001 Ω。

自抗扰解耦控制器的参数按照以下方法进行配置：由HE等[12]的研究可知较大的w0可以加速扰动的消除，通常选择w0=10wc，借鉴袁东[13]所提配置方法，运用试凑法对参数进行配置。得有功功率控制器w01=18，wc1=1.8，b01=0.43；无功功率控制w02=800，wc2=80，b02=0.4。直流侧电容电压参考值udc=800 V。

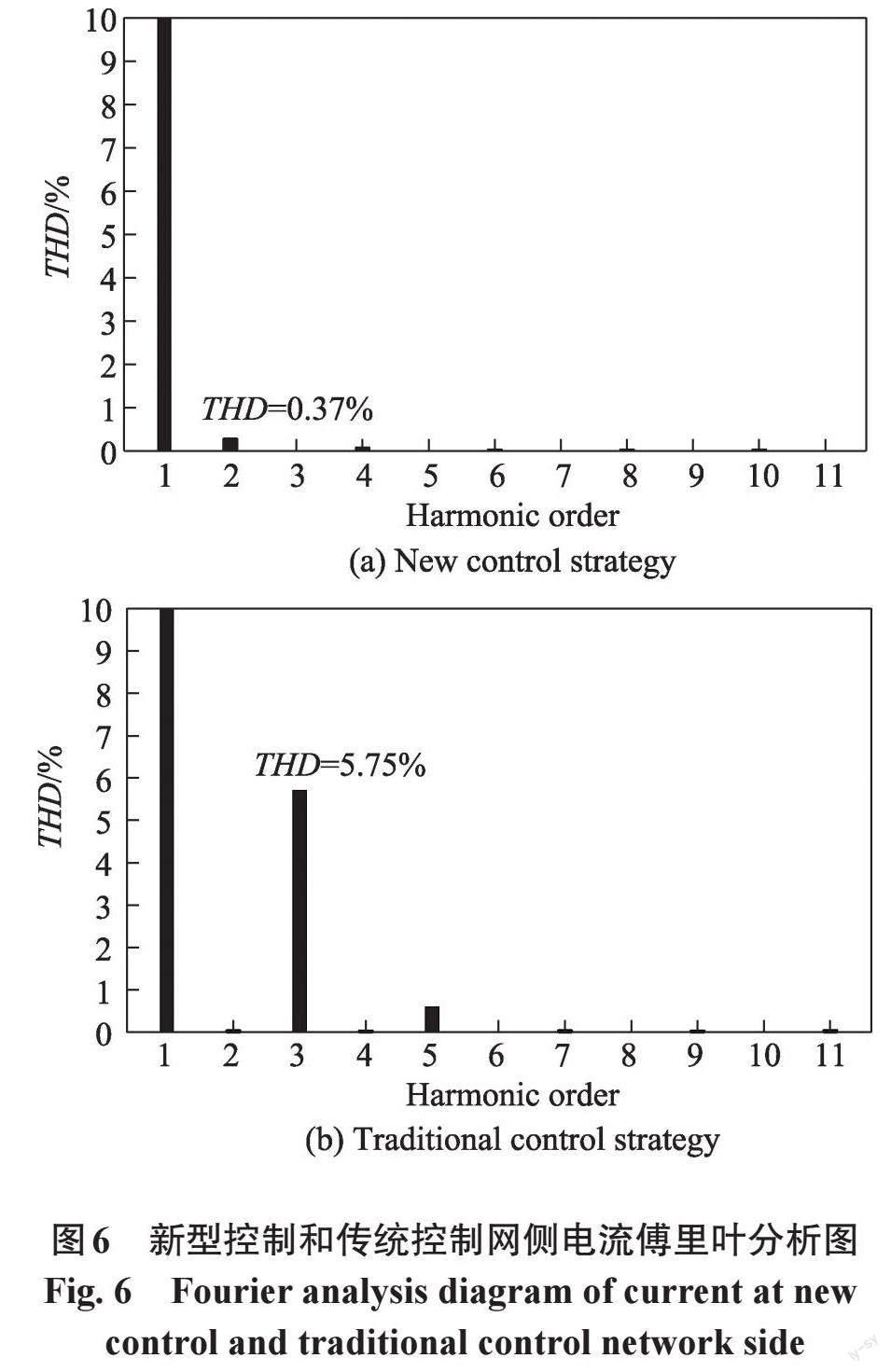
4.1 网侧电流THD分析

为比较传统控制策略与新型控制策略的谐波抑制能力，对系统稳定时网侧电流进行傅里叶分析。图6（a）为采用新型控制策略时的傅里叶分析图，THD值为0.37%。图6（b）为采用传统控制策略时的傅里叶分析图，THD值为5.75%。对比可得，采用新型控制策略时系统的THD值减小5.38%，谐波抑制效果显著，由此可知新型控制策略有着更好的谐波抑制能力。

4.2 负载突变及负载不平衡仿真

当负载R1，R2，R3均是100 Ω时，在t=0.8 s时将负载突变为R1=130 Ω，R2=160 Ω，R3=190 Ω时验证负载突变时的控制效果。取R1=100 Ω，R2=150 Ω， R3=200 Ω时验证负载不平衡时控制效果。仿真结果如图7所示。

由图7可知文章所采用控制策略在负载突变和负载不平衡工况下电容电压仍能保持平衡。

4.3 等效电感突变分析

等效电感突变对系统的平衡有着巨大影响，为探究新型控制策略应对这一状况的能力。在t=0.7 s时，在电感L=5 mH的基础上并联一个2 mH的电感，并将两种控制策略进行仿真对比，结果如图8所示。

由图8可知，采用新型控制策略控制的系统，电压最低跌落至768 V，与稳态相差32 V，在0.6 s后即可逐渐恢复至稳定状态。而采用传统控制策略的系统，直流侧电压最低跌落至720 V，与稳态相差80 V，需要1.3 s才能逐渐恢复到稳定状态。通过对比仿真结果得出文中所提新型控制策略相较于传统控制策略能更好应对电感参数变化带来的影响。

4.4 网侧电压频率偏移对比分析

为比较两种控制策略对电压频率偏移的应对能力，做频率偏移仿真对比。将系统仿真频率初始值设置为49.5 Hz，在0.48 s至0.68 s期间，以5 Hz/s的速度偏移至50.5 Hz，0.68 s后保持频率不变。仿真结果如图9（a）和图9（b）所示。

从图9（a）和图9（b）中可以看出，当新型控制策略控制的系统发生频率偏移时，直流侧电压最大跌落值为53 V。而以传统控制策略控制的系统发生频率偏移时，直流侧电压最大跌落值可以达到67 V，且后续的波形稳定性不如以新型控制策略控制的系统。通过对比仿真结果可以得出传统控制策略在应对频率偏移时不如文章所提新型控制策略。

5 结论

1） 文章所提新型控制策略通过自抗扰解耦实现了有功功率和无功功率的独立控制。

2） 新型控制策略下系统的网侧电流THD值更小，在负载突变与负载不平衡工况下仍能保持稳定。

3） 新型控制策略在应对电感参数变化、网侧电压频率偏移时比传统控制策略效果更好。

参考文献：

[1]   ZHANG H， WANG Y， ZHANG G， et al. Research on LADRC strategy of PMSM for road-sensing simulation based on differential evolution algorithm[J]. Journal of Power Electronics， 2020， 20： 958-970.

[2]   GAO Z Q. Scaling and bandwidth-parameterization based controller tuning[C] //Proceedings of the American Control Conference. Denver： IEEE， 2003： 4989-4996.

[3]   NAIR R R， BEHERA L. Robust adaptive gain higher order sliding mode observer based control-constrained nonlinear model predictive control for spacecraft formation flying[J]. IEEE/CAA Journal of Automatica Sinica， 2018， 5（1）： 367-381.

[4]   陳增强， 程赟， 孙明玮， 等. 线性自抗扰控制理论及工程应用的若干进展[J]. 信息与控制， 2017， 46（3）： 257-266.

CHEN Z Q， CHENG Y， SUN M W， et al. Surveys on theory and engineering applications for linear active disturbance rejection control[J]. Information and Control， 2017， 46（3）： 257-266.

[5]   于雁南， 杨荣峰， 严继池， 等. 级联H桥静止无功发生器的多变量自抗扰解耦控制[J]. 中国电机工程学报， 2016， 36（8）： 2233-2241.

YU Y N， YANG R F， YAN J CH， et al. Multiple-input multiple-output decoupling control schemes of static var gen-erator with cascaded H-bridge based on active disturbance rejection control[J]. Proceedings of the CSEE， 2016， 36（8）： 2233-2241.

[6]   付文强， 赵东标， 张瑶. 改进型自抗扰解耦的PMSM调速控制方法研究[J]. 机械科学与技术， 2022， 41（4）： 646-650.

FU W Q， ZHAO D B， ZHANG Y. Research on PMSM speed regulation method of improved active disturbance rejection decoupling[J]. Mechanical Science and Technology for Aerospace Engineering， 2022， 41（4）： 646-650.

[7]   张先勇， 吴捷， 杨金明. 基于自抗扰解耦的变速恒频风力发电功率控制系统[J]. 电气传动， 2007（2）： 8-11.

ZHANG X Y， WU J， YANG J N. Power control strategy based on auto-disturbance rejection decoupling for a variable speed constant frequency generation system[J].  Electric Drive， 2007（2）： 8-11.

[8]   宋平岗， 连加巍， 陈怡. 单相电力电子变压器整流级新型直接功率控制策略[J]. 控制理论与应用， 2022， 39（3）： 402-410.

SONG P G， LIAN J W， CHEN Yi. Single-phase power electronic transformer rectifier stage new direct power control strategy[J]. Control Theory & Applications， 2022， 39， （3）： 402-410.

[9]   宋平岗， 林家通， 李云丰， 等. 基于模块化多电平的铁路功率调节器直接功率控制策略[J]. 电网技术， 2015， 39（9）： 2511-2518.

SONG P G， LIN J T， LI Y F， et al. Direct power control strategy of railway power conditioner based on modular multilevel. Power Grid Technology， 2015， 39（9）： 2511-2518.

[10] 宋平岗， 陈怡， 连加巍. 基于LESO的MMC-RPC反馈线性化直接功率控制[J/OL]. 控制理论与应用： 1-8. [2023-02-18].http：//kns.cnki.net/kcms/detail/44.1240.TP.20220617. 1847.006.html.

SONG P G， CHEN Y， LIAN J W. Feedback linearization direct power control of MMC-RPC based on linear extended state observer[J/OL]. Control Theory & Applications：1-8. [2023-02-18].http：//kns.cnki.net/kcms/detail/44.1240.TP. 20220617. 1847.006.html.

[11] 袁义生， 陈旭. 级联H桥整流器输出电压平衡控制策略研究[J]. 电力电子技术， 2020， 54（2）： 16-19.

YUAN Y S， CHEN X. Research on cascaded H-bridge rectifier output voltage balance control strategy[J]. Power Electronics， 2020， 54（2）： 16-19.

[12] HE T， WU Z L， Li D H， et al. A tuning method of active disturbance rejection control for a class of high-order process[J]. IEEE Transaction on Industrial Electronics， 2019， 67（4）： 3191-3201.

[13] 袁東， 马晓军， 曾庆含， 等. 二阶系统线性自抗扰控制器频带特性与参数配置研究[J]. 控制理论与应用， 2013， 30（12）： 1630-1640.

YUAN D， MA X J， ZENG Q H， et al. Research on frequency-band characteristics and parameters configuration of linear active disturbance rejection control for second-order systems[J]. Control Theory & Applications， 2013， 30（12）： 1630-1640.

通信作者：宋平岗（1965─），男，教授，博士生导师，研究方向为大功率电力电子技术，风力及光伏发电，能源互联网。E-mail： pgsong@ecjtu.edu.cn。