基于数控工艺信息挖掘的型腔特征粗加工刀具序列优化决策方法
徐昌鸿,张树生,梁嘉宸
(1.南京工程学院 工业中心, 江苏 南京 211167;2.西北工业大学 机电学院, 陕西 西安 710072)
0 引言
随着智能制造的浪潮席卷全球,制造业相继引入了多种数字化、智能化的生产制造手段,以提升产品竞争力[1]。其中,智能数控工艺设计是一个极其重要的环节[2]。而加工刀具优化决策一直以来都是数控工艺设计的基础,合理、高效的刀具选择能够显著提升产品生产效率、缩短研制周期、降低生产成本[3]。另一方面,型腔特征是数控加工中最常见的特征类型之一,其粗加工时间通常占总加工时间70%以上甚至更多[4]。因此,型腔特征粗加工刀具的选择对数控加工效率具有重要的影响[5]。目前,生产车间粗加工刀具选择仍然以人工决策方式为主,主要依赖于工艺人员依据自身经验知识对特征形状、尺寸、加工精度等信息进行分析,存在智能化程度低、精度差、加工效果不理想等缺点。如何更智能、高效地进行型腔特征粗加工刀具序列优化决策,已经成为智能数控工艺设计亟需解决的关键问题之一。
随着信息技术的发展,近年来学术界陆续提出多种刀具序列优化决策方法,如Voronoi图法[6]、几何分析法[7]、实例推理法等[8]。ZHAO等[9]以加工能耗为优化目标,提出一种基于数字控制产品模型数据交换标准(Standard for the Exchange of Product model data for Numerical Control,STEP-NC)的铣削刀具选择方法。该方法在STEP-NC标准框架下构建刀具参数和加工能耗的关联模型,采用遗传算法进行优化求解,获得最优刀具组合。DUAN等[10]提出一种基于加工工艺知识图谱的刀具序列决策方法。该方法采用Web本体语言(Web Ontology Language,OWL)建立加工工艺的本体模型及知识图谱,然后构建一个描述“制造特征-材料-加工刀具”关系的数据模型,采用个性化PageRank算法求解加工刀具组合。ZHOU等[11]提出一种基于深度学习的复杂形状零件加工刀具选择方法,分析制造特征与加工刀具之间的一一对应关系,将刀具选择问题转化为制造特征识别问题。同时,由于数控机床大多采用加工中心形式,其配备的刀库涵盖的刀具范围较为广泛,如采用圆盘刀库可以安装24把刀具,配备链式刀库则最多可以安装一两百把刀具,因此进行加工刀具序列选择时存在规模巨大的排列组合情形,属于NP难问题,采用智能优化算法进行求解可以在较短时间内获得较好的结果,已经在生产加工中得到了充分应用[12]。周能等[13]提出一种基于遗传算法的火箭贮箱壁板数控加工刀具选择优化方法。该方法以加工时间为优化目标,构建刀具切削过程的时间耗费模型,采用遗传算法求解最优刀具数量和切削直径。这些方法为解决刀具优选问题提供了有效的解决思路。但是,已有方法大多构建单目标优化模型,未能充分考虑数控加工中的多方面影响因素;且主要考虑制造特征的几何形状、尺寸等低层次信息,未能深入挖掘三维 CAD模型中更高层次的隐式数控工艺信息[14],优化计算模型不能有效反映刀具切削运动过程;同时,仍然依赖于启发式规则进行判定[15],自动化程度不高,导致得到的刀具序列实用性不强。
中轴变换作为几何图形的有效描述符,通过提取其骨架信息,将图形等分为对称的两部分,可作为刀具轨迹的有效参考,已经在数控加工领域得到了广泛应用[16-17]。CHEN等[18]基于中轴变换算法计算型腔特征的加工区域范围,以加工时间最短为目标,优化求解得到最优刀具序列,并生成相应的刀具轨迹。杨梦媛等[19]针对框、梁、壁板、蒙皮等飞机关键零部件中型腔特征的高速切削,提出一种基于中轴变换的刀具轨迹生成方法,保证了刀轨平滑无抬刀及步距在容许范围内平稳变化。巴文兰等[20]基于型腔特征中轴变换函数,优化选择粗加工刀具序列及清角/清根刀具,并自动生成相应的环切法刀具轨迹路线。目前,大部分研究集中在中轴变换的轮廓偏置计算和数学建模方面,尚缺乏如何将中轴变换与数控加工过程进行有效关联映射的探索,无法有效支撑智能工艺设计的应用落地。
由于3D型腔通常采用平底铣刀进行分层加工,可以看作2.5D型腔的逐层叠加组合,因此2.5D型腔粗加工刀具优化决策是基础。本文以2.5D型腔特征为研究对象,提出基于数控工艺信息挖掘的型腔特征粗加工刀具序列选择优化方法。首先,引入中轴变换作为刀具轨迹,分析中轴变换与数控加工的映射机理;然后,依据数控加工规则,基于映射机理挖掘反映加工过程内涵的数控工艺信息,包括容许刀具集、退刀次数、有效切削面积等;最后,构建多目标优化模型及备选刀具有向图,采用混合蚁群/模拟退火算法求解,获得最优粗加工刀具序列。
1 基本概念与方法概述
1.1 基本概念
定义1型腔特征边界曲线图。型腔特征F的边界曲线图G是中轴变换计算的输入条件,包括两部分:主特征轮廓边界曲线G′和辅助特征(孔、凸台等)外轮廓边界曲线G″,定义为:
(1)
其中,G(H)i″为孔特征的外轮廓边界曲线,P为孔特征数量;G(B)j″为凸台特征的外轮廓边界曲线,Q为凸台特征数量。
如图1所示为型腔特征F及其特征边界曲线图(蓝色实线)和中轴线(红色实线)。
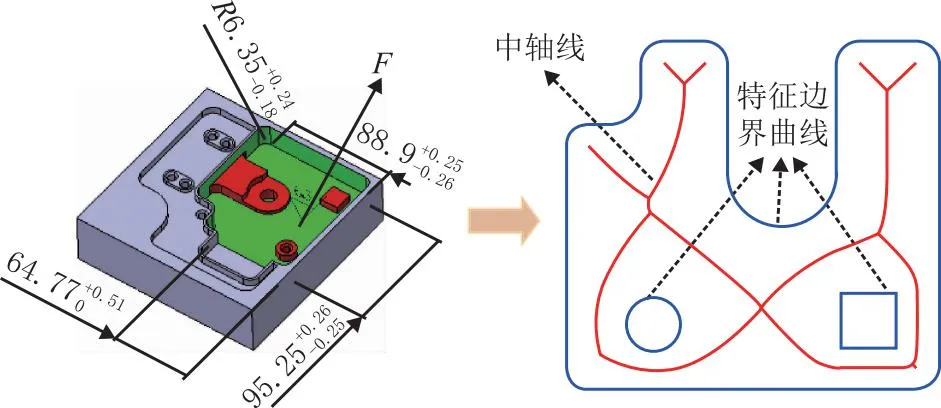
图1 型腔特征边界曲线图

图2 本文方法总体流程
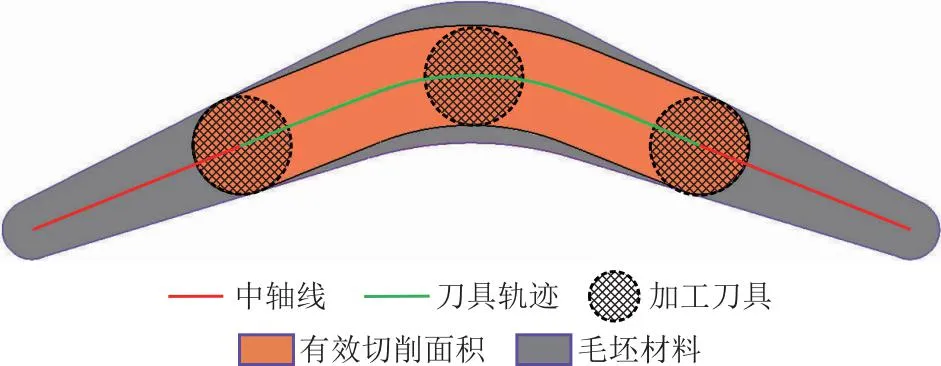
图3 有效切削面积计算示意图(δ=0)
定义2容许刀具集(Allowable Tools Set,ATS)。特征F的容许刀具集 [F]ATS表示适用于F粗加工的所有刀具按切削直径由大到小顺序组成的集合,定义为:
(2)
其中,N为刀具数量,Di表示刀具切削直径(后文简称刀具直径)。
定义3充分刀具和必要刀具。[F]ATS中刀具直径最大值DL和最小值DS分别定义为F的充分刀具和必要刀具。
1.2 方法概述
本文方法的总体流程如图 2所示,主要包括中轴变换与数控加工的映射机理、基于映射的数控工艺信息挖掘、刀具序列优化决策求解3部分,具体地:
(1)中轴变换与数控加工的映射机理 该部分采用文献[21]中特征识别算法,识别三维CAD模型型腔特征及其边界曲线图,该部分内容本文不作详细描述。引入中轴变换作为刀具轨迹并计算相关参数,分析中轴变换与数控加工的映射机理,包括中轴变换与刀具选择映射及中轴变换与加工连续性映射。
(2)基于映射的数控工艺信息挖掘 该部分基于映射机理,结合刀具选择约束条件及刀具切削运动规律,挖掘计算容许刀具集、退刀次数、有效切削面积等隐式数控工艺信息。
(3)刀具序列优化决策求解 该部分提出综合考虑材料去除量和加工连续性的多目标优化模型,构建备选刀具有向图表征刀具加工过程,采用混合蚁群/模拟退火算法对备选刀具有向图进行搜索,获得最优粗加工刀具序列。
本文构建的优化模型涉及到的符号和变量注释如下:
F为型腔特征;
[F]ATS为F的容许刀具集;
Di为刀具切削直径;
DL、DS为[F]ATS中的充分刀具和必要刀具;
dmax、dmin为局部内切圆直径的最大值、最小值;
Pi为中轴线片段;
δ为粗加工余量;
MT为中轴变换与刀具选择映射;
MC为中轴变换与加工连续性映射;
Lj(Di)为刀具Di的第j条有效刀具路径;
s为中轴线被有效刀具路径分割形成的线段数量;
ψ(Di)为Di的退刀次数;
Aj为第j次退刀;
Ms×ψ(Di)为中轴变换和退刀次数映射矩阵;
Sj(Di)为Di沿Lj(Di)的有效切削面积;
S(Di)为Di的整体有效切削面积;
[T]Center为当前加工中心中的刀具集合;
TC(F)为F的备选刀具集(即优化模型解空间);
S(Di→j)为先采用Di后采用Dj进行加工时Dj的实际有效切削面积;
TS(F)为F的最优粗加工刀具序列;
n为TS(F)中的刀具数量。
2 中轴变换与数控加工的映射机理
2.1 中轴变换参数计算
由文献[18]可知,型腔特征F的中轴变换本质是满足与型腔特征边界曲线相切的一系列局部内切圆,其圆心依次相连接形成的连续曲线和直线集合,可以定义为:
(3)
其中:M为局部内切圆数量,ω(O(xi,yi),di)为局部内切圆方程;基于中轴变换,全体局部内切圆圆心坐标O(xi,yi)及直径di易于计算得到,其中直径最大最小值分别为dmax和dmin。
2.2 映射机理分析
从数控加工角度考虑,型腔特征F的中轴线Pi作为刀具轨迹,在dmin对应的最小局部内切圆圆心位置O(xmin,ymin)处,刀具的可切削范围最小,且随着刀具直径增大,刀具首先在此处与轮廓发生干涉。因此,只有直径不大于dmin-2δ(δ为粗加工余量)的刀具才可以沿着Pi无干涉完成特征区域的整体粗加工。同理,在dmax对应的最大局部内切圆圆心位置O(xmax,ymax)处,当刀具直径超过dmax-2δ时,刀具沿Pi任一部分移动都将产生干涉,无法满足特征加工要求。这就意味着,只有直径不大于dmax-2δ的刀具才可以沿Pi对特征部分区域进行粗加工。
可以看出,型腔特征F的中轴变换参数dmax和dmin描述了刀具切削运动的限制范围,反映了F粗加工时的刀具选择约束条件,有效表征了中轴变换与数控加工之间的映射机理。依据形式不同,映射机理分为中轴变换与刀具选择映射(MT)和中轴变换与加工连续性映射(MC)。
3 基于映射的数控工艺信息挖掘
依据上述映射机理两种形式,可实现型腔特征中更高层次隐式数控工艺信息的挖掘提取,包括容许刀具集、退刀次数和有效切削面积等。
3.1 容许刀具集
数控加工中刀具选择的一个重要原则就是刀具不能与特征的边界发生过切或干涉。依据上述分析,只有当刀具直径Di≤dmax-2δ,Di才可用以型腔特征F的粗加工。由于Di是非整数的情形较少,本文暂不考虑。因此,为了确保加工质量满足要求,充分刀具DL可定义为

(4)

另一方面,任意刀具直径Di≤dmin-2δ都可以沿整体中轴线无干涉粗加工F所有区域。然而,若Di过小,则额外增加了走刀次数,造成不必要的工时浪费。因此,必要刀具DS可定义为

(5)
表明DS取小于或等于dmin-2δ的最大整数。
综上,中轴变换与刀具选择约束映射MT可以表示为
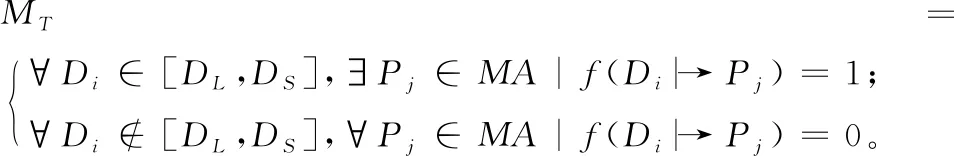
(6)
其中:“∀”表示“任意”,“∃”表示“存在”,f(Di|→Pj)=1表示刀具Di沿一段中轴线Pj加工F时不发生干涉过切;否则,f(Di|→Pj)=0。上式表明,对于任意一把切削直径属于[DL,DS]范围内的刀具Di,则必存在一段中轴线Pj,使得Di能够沿Pj粗加工F同时不发生干涉过切,意味着Di可用以F的粗加工;相反地,对于任意一把切削直径不属于[DL,DS]范围内的刀具Di,当其沿任意一段中轴线Pj进行切削时,总会发生干涉过切,则Di无法用以F粗加工。因此,F的容许刀具集[F]ATS可以表示为
[F]ATS={Di|Di=DL-i,
i=0,1,2,3…,(DL-DS)}。
(7)
3.2 退刀次数
中轴变换与加工连续性映射反映了刀具切削过程的连续性,对加工结果具有重要影响,常以退刀次数作为参考指标。对于刀具Di∈[F]ATS,加工F时产生的一条有效刀具路径Lj(Di)的本质是直径不小于Di+2δ的一系列局部内切圆{ω(Ok(xk,yk),dk)|dk≥Di+2δ, 0≤k≤K},其圆心{Ok(xk,yk)}按顺序依次连接形成的一条连续曲线或直线。F的全体中轴线被有效刀具路径分割为若干段。当刀具Di沿一条有效刀具路径完成切削运动,需要进行退刀操作从而移动到下一条。因此,Di加工F过程中的退刀次数,即为其产生的有效刀具路径数量,则中轴变换与加工连续性映射MC可以表示为
(8)
其中:s为中轴线被有效刀具路径分割形成的线段数量;Pi为第i段中轴线;ψ(Di)为Di的退刀次数;Aj为第j次退刀;Ms×ψ(Di)为中轴变换和退刀次数映射矩阵,mij=1表示刀具沿第i段中轴线完成加工后产生第j次退刀。
3.3 有效切削面积
粗加工目的在于尽可能以高效率去除更多的材料,因此,材料去除量是进行粗刀具加工选择的一项重要参考指标。由于2.5D型腔在同一特征内深度通常相同,本文采用有效切削面积表征材料去除量。对于刀具Di的一条有效刀具路径Lj(Di),其有效切削面积是以Ok(xk,yk)为圆心,以Di为半径的圆沿Lj(Di)运动所覆盖的区域面积,如图 3所示。本文采用文献[18]方法,结合OpenGL接口函数[22],实现有效切削面积的近似计算。Di沿Lj(Di)的有效切削面积Sj(Di)可以定义为
Sj(Di)=Function(Lj(Di),Di,δ)。
(9)
由于Di的有效刀具路径数量和退刀次数相同,则Di的整体有效切削面积S(Di)可以表示为
(10)
4 刀具序列优化决策求解
4.1 多目标优化模型
由上述分析可知,在粗加工中,若单独采用大直径刀具,则无法完整加工特征区域,从而导致后续精加工切削量大;而单独采用小直径刀具,则有效切削面积少,需要反复多次加工。两种方法都会导致加工时间长、效率低。另一方面,现代数控机床加工中心换刀时间较短,对生产周期的影响可以忽略不计。因此,粗加工中大多采用多刀具组合加工策略,即首先采用大刀具高效切除大部分材料,然后采用小刀具切除剩余材料直至达到余量要求。
本文基于挖掘得到的数控工艺信息,综合考虑材料切削量和加工连续性,以有效切削面积和退刀次数为目标构建优化模型。由前述分析可知,只有必要刀具DS才能完成型腔特征整体区域粗加工,以达到最终的余量要求。因此,通常DS是加工中心刀库中必备刀具,也是任意刀具序列必须选择的最后一把刀具。若当前加工中心中刀具集合为[T]Center,则型腔特征F的备选刀具集(即优化模型的解空间)TC(F)=[F]ATS∩[T]Center={D1,D2, …,Di,…,Dj…,DS},且刀具直径由大到小排列,即D1>D2>…,>Di…>Dj…>DS。依据公式和计算可得任意一把刀具Di(Di∈TC(F))单独加工时的有效切削面积S(Di)和退刀次数ψ(Di)。特别地,由于Di在Dj之前加工,且单独加工时Di的刀具轨迹必然是Dj的子集,则组合加工时Dj的部分刀具轨迹已由Di完成切削,Dj的实际有效切削面积S(Di→j)应自适应调整为Dj与Di分别单独加工时有效切削面积的布尔差(如图4),表示为:
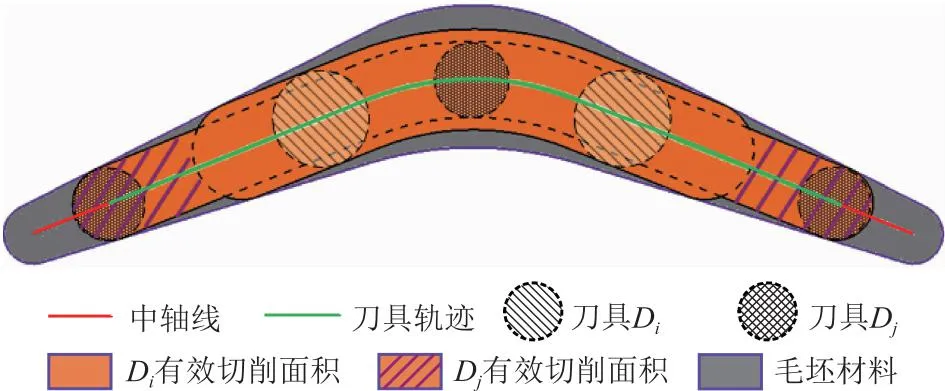
图4 组合刀具加工的有效切削面积示例
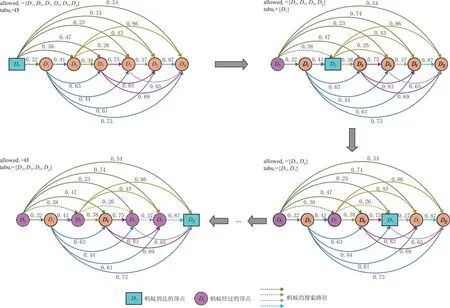
图5 基于CTG的蚁群算法示例
S(Di→j)=Subtraction(S(Dj)-S(Di))。
(11)
本文的优化目的即为从TC(F)中寻找最优子集TS(F),满足按顺序选用TS(F)内刀具进行粗加工时有效切削面积总体最大同时退刀次数总体最少。因此,本文的多目标优化模型表示为
max:S(TS(F)),min:ψ(TS(F));
s.t:
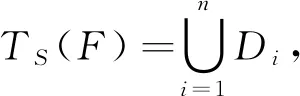
(12)
4.2 备选刀具有向图
定义4备选刀具有向图(Candidate Tools Graph, CTG)。备选刀具有向图CTG是一个描述采用备选刀具集TC(F)中各刀具进行粗加工过程中型腔特征形态更迭的带权有向图。其中:顶点D0表示型腔特征初始毛坯状态,对应刀具直径为+∞,其余顶点表示TC(F)中的加工刀具。任意两顶点之间都存在有向边,方向由大刀具指向小刀具,表征了加工刀具选择的顺序约束条件。CTG可以定义为
(13)
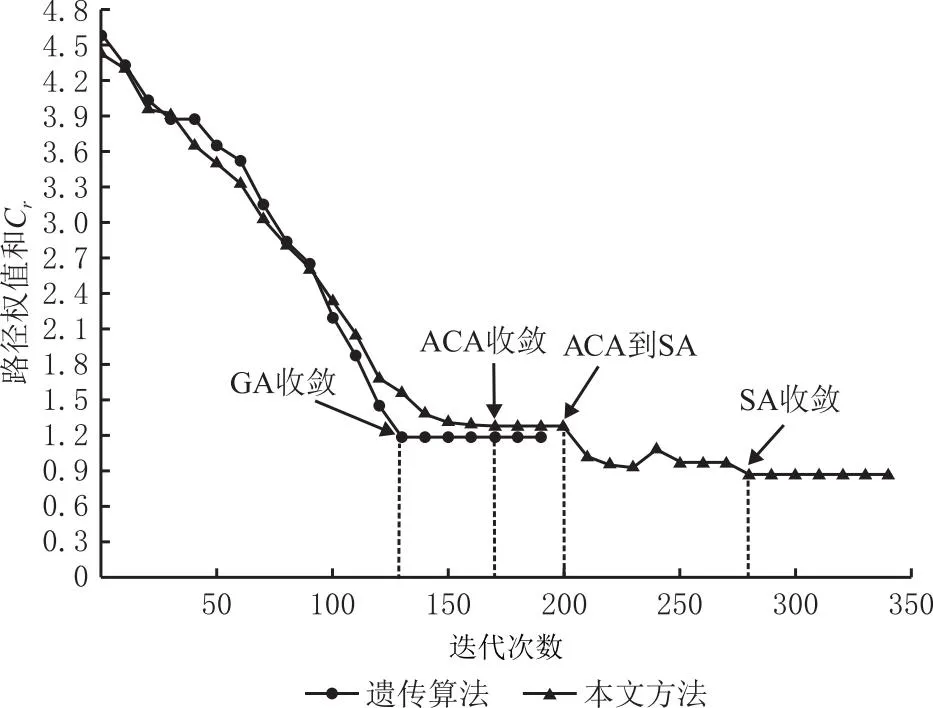
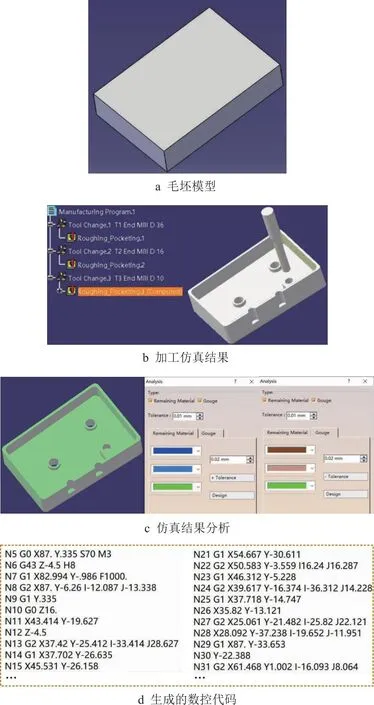
(1)计算所有有向边权值{Dis(Di,Dj)}={S(Di→j),ψ(Di→j)}(0≤i≤x-1,i (2)分别取{S(Di→j)}中最大值Smax和{ψ(Di→j)}中最大值ψmax,针对{S(Di→j)}和{ψ(Di→j)}中元素进行如下归一化处理 (14) (3)新权值集合{S(Di→j)′,ψ(Di→j)′}中各元素都位于[0,1]之间,且无量纲,因此,可以定义权值Dis(Di,Dj)如下 (15) 其中ω1和ω2分别表示材料切削量和加工连续性重要程度的权重,由工艺人员启发式制定,本文ω1=0.6,ω2=0.4。 依据上述方法构建的CTG,其中任意一条以D0为起点,以DS为终点的连通路径,都对应一个可行的刀具序列,其中最短路径对应的刀具序列组合即为最优解。因此,刀具序列优化问题转化为最短路径搜索问题。相应地,初始构建的多目标优化模型(式12)转化为以路径最短为目标的单目标优化模型,可以表示为: min:Cr(TS(F)); s.t. (16) 其中Cr(TS(F))表示刀具序列TS(F)对应CTG中的路径权值之和。 本文充分利用蚁群算法较好的路径搜索能力和模拟退火算法较强的全局搜索特性[23],提出一种混合蚁群/模拟退火算法:首先通过蚁群算法搜索得到若干较优路径,然后采用模拟退火算法跳出局部收敛,得到最终的全局最优解。 4.3.1 蚁群算法 在t时刻,蚂蚁r从顶点Di移动到Dj的概率pij(t)定义为 (17) 其中:allowedr表示蚂蚁下一步可访问顶点集合,是保证搜索路径有效性的关键约束条件,本文中即为备选刀具集中位于Di之后的刀具集合,即allowedr={Di+1,Di+2,…,DS};τij(t)为t时刻有向边E(Di,Dj)上的信息素含量,初始为0;ηij为蚂蚁从Di移动到Dj的期望值,定义为1/Dis(Di,Dj)。α和β分别表示信息启发因子和期望值启发因子,本文α=1,β=5。 蚂蚁搜索完成后,各有向边信息素浓度按如下方式自适应更新: (18) 依据上述分析,基于CTG的蚁群算法步骤如下: 输入:备选刀具有向图G; 输出:最优刀具序列集TP,初始为空。 步骤2将蚂蚁r放在初始顶点D0上,依据公式(17)选择蚂蚁下一步到达顶点Di。 步骤3如果Di=DS,结束搜索,转到步骤6;否则,转到步骤4。 步骤4将Di放入禁忌列表tabur,自适应计算更新allowedr,依据式(17)选择蚂蚁下一步到达顶点Dj。 步骤5重复Step4直至Dj=DS,结束搜索。 步骤6计算搜索路径Pathr的权值总和Cr。 步骤7若Cr 步骤8如果r 步骤9若I 其中a←b表示将b的数值赋予a。 如图 5所示为算法示例。首先,蚂蚁从初始顶点D0出发,依据式(17)选择到达顶点D2,此时将D2放入禁忌列表,同时自动计算allowedr={D3,D4,D5,DS},作为蚂蚁下一步搜索的约束条件。继续选择蚂蚁下一步到达顶点D4,则将D4放入禁忌列表,同时allowedr自适应更新为{D5,DS},重复搜索直至蚂蚁到达DS,则此蚂蚁搜索路径为{D2,D4,D5,DS}。本方法以选择刀具直径递减为准则,保证搜索过程准确、高效进行。 4.3.2 模拟退火算法 由于蚁群算法后期易陷入局部收敛,其搜索得到的较优解多为局部最优,距离全局最优解尚有差距。另一方面,模拟退火算法在优化过程中能够以一定概率跳出局部收敛点继续搜索,增加了获得全局最优解的概率。因此,本文以蚁群算法得到的最优刀具序列集TP中最优的M(本文取M=15)个解为输入,采用模拟退火算法,通过概率性位置刀具变异生成新解Yi,即从备选刀具集中随机选择一把刀具Di(Di∉Yi)替代Yi中任一位置刀具(D0和DS除外),进行进一步的全局搜索。特别地,由于刀具变异可能导致生成的新解不符合刀具直径由大到小排列的约束要求,本文提出一种自适应修正算法,调整不可行新解,步骤如下: 步骤1初始化。设置起始温度T0= 100,终止温度T1=T0×α1000,降温系数α=0.999 5,刀具变异概率PT=0.35。 步骤2针对变异位置Dj′,若Dj+1 步骤3按顺序遍历{Dj+2,Dj+3,…,DS},找到第一个位置Dk 步骤4按顺序遍历{Dj-2,Dj-3,…,D1},找到第一个位置Dk>Dj′, 将Dj′从当前位置转移到Dk之后,转至步骤5。 步骤5重复步骤2~步骤4,直至所有变异位置都修正完毕,输出Yi进行后续计算。 为有效验证本文所提方法的合理性,以Microsoft Visual Studio 2008为集成开发工具,在CATIA CAA环境中实现了本文算法,并在Intel(R) Core(TM) i7-11800H@2.3 GHz的PC机上进行了测试。 图6 数控工艺信息挖掘实例 5.2.1 实例介绍 如图7所示为某制造企业的典型型腔特征F2及其中轴变换,计算可得[F2]ATS=[57,10](δ=0.5)。生产车间采用MAZAK七轴五联动车铣复合加工中心,包括多把平底钨钢铣刀,[T]Center={2,4,5,6,8,10,12,16,18,20,24,28,32,36,42,48,54,60,64,68,74,78}。则备选刀具集TC(F2)=[F2]ATS∩[T]Center={54,48,42,36,32,28,24,20,18,16,12,10}。 5.2.2 计算结果 依据本文方法,计算可得最优粗加工刀具序列为{D36,D16,D10},有效切削面积∑S=9693.31,退刀次数∑ψ=19。若采用常规人工决策方法,则刀具序列为{D42,D24,D10},有效切削面积∑S=8 154.36 mm2,退刀次数∑ψ=21。两种方法决策结果对应的刀具轨迹如图8和图9所示,计算结果如表1所示。可以看出,本文方法在材料切削量和加工连续性方面都优于常规方法,各有18.87%和9.52%的效率提升。 表1 两种方法计算结果 图8 本文方法决策结果的刀具轨迹 图9 常规方法决策结果的刀具轨迹 为进一步比较本文方法和常规方法的粗加工刀具序列决策能力,本文选择3个形状不同且复杂度递增((即岛屿数量增加导致中轴变换规整程度下降)的型腔特征P1、P2、P3,针对刀具数量为2、3、4、5的情形,分别采用两种方法计算,结果如表2所示。分析可知,复杂度越高的型腔特征,采用本文方法的效率提升越高。这是因为复杂度高的型腔特征,其中轴线分叉多、扭曲程度大,导致内部狭窄通道多,若刀具直径过大则无法通过多处狭窄区域从而引起更多退刀次数,而过小则导致有效切削面积减少。常规方法依据工艺设计人员的经验直觉,无法在二者之间做到较好的平衡,而本文方法综合考虑有效切削面积和退刀次数,构建多目标优化模型进行优化求解,取得了很好的效果。同时,由于本文方法通过引入中轴变换作为刀具轨迹,挖掘深层次数控工艺信息并采用智能优化算法进行决策,整个过程以计算机运算为主,平均耗费时间不超过10 s。而常规启发式方法需要大量的人工交互判断,平均耗时分别高于500 s、900 s、1 500 s,远多于本文方法,因此计算速度慢、效率低。 表2 两种方法计算结果对比分析 如图10所示为采用本文方法的3个型腔特征计算结果曲线图。可以看出,随着刀具数量增加,有效切削面积和退刀次数也随之增加。但当刀具数量到达一定阈值(P1、P2为3,P3为4)后,有效切削面积增幅不显著,但是退刀次数依然明显增大,反而影响加工效率。这是因为刀具数量过大,会导致各刀具之间重叠的切削区域过多,小刀具的有效切削面积少,额外增加换刀次数。因此,在数控工艺设计中,针对不同的型腔特征,需要优化决策采用不同数量的最优刀具组合,这也是常规方法难以有效实现的。 图10 本文方法的计算结果曲线图 图11所示为本文方法和遗传算法(Genetic Algorithm,GA)针对图 7型腔特征的迭代过程对比图。可以看出,遗传算法易于陷入局部收敛,收敛速度快(迭代130次即达到收敛)但是优化结果不够理想,Cr=1.19仅为较优解。本文方法综合蚁群算法和模拟退火算法的优势,首先采用蚁群算法进行搜索获得若干较优解,然后采用模拟退火算法跳出局部收敛获得全局最优解,迭代收敛次数为281,优化目标值Cr=0.87,在计算速度和优化结果方面取得了良好的平衡效果。 图11 本文方法和遗传算法的迭代过程对比图 为了验证本文方法刀具序列优化决策结果的有效性和可靠性,将图 7型腔特征三维CAD模型及其最优刀具序列{D36,D16,D10}在CATIA数控加工模块中进行仿真测试(图12)。图 12a所示为毛坯模型,图12b为加工仿真获得的最终型腔特征。通过分析加工仿真结果可以看出,型腔特征不存在欠切和过切情况,表面质量符合设计要求(图12c)。这就意味着,最优刀具序列可以满足实际数控加工需要。在CATIA中生成FANUC 16B数控系统相对应的数控代码,如图12d所示,可直接传递至下游的车间进行数控加工。 图12 加工仿真分析 本文提出一种基于数控工艺信息挖掘的型腔特征粗加工刀具序列优化决策方法。首先,引入中轴变换描述型腔特征的刀具轨迹,将中轴变换与数控加工过程进行有效映射;然后基于数控加工规则自动挖掘提取隐含的数控工艺信息;最后,构建备选刀具有向图表征所有可行刀具的切削过程,提出一种混合蚁群/模拟退火算法进行优化搜索,获得最优粗加工刀具序列。实验结果表明,本文方法通过充分挖掘三维CAD模型中隐式存在、深层次反映数控加工内涵的容许刀具集、退刀次数、有效切削面积等数控工艺信息,得到的刀具序列决策结果更加可靠有效,且计算效率、自动化程度较高,对智能数控工艺设计的发展具有重要的科学意义与工程应用价值。 下一步工作包括:①考虑引入深度学习等数据挖掘分析算法,进一步探索3D型腔特征中轴变换与数控加工的映射机制,扩展本文方法的适用范围;②深入研究挖掘更丰富的隐式数控工艺信息,如加工策略、切削参数等,进一步提升本文方法的实用性。4.3 混合蚁群/模拟退火算法
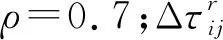
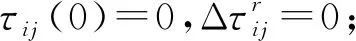
5 算法验证与讨论
5.1 数控工艺信息挖掘实例

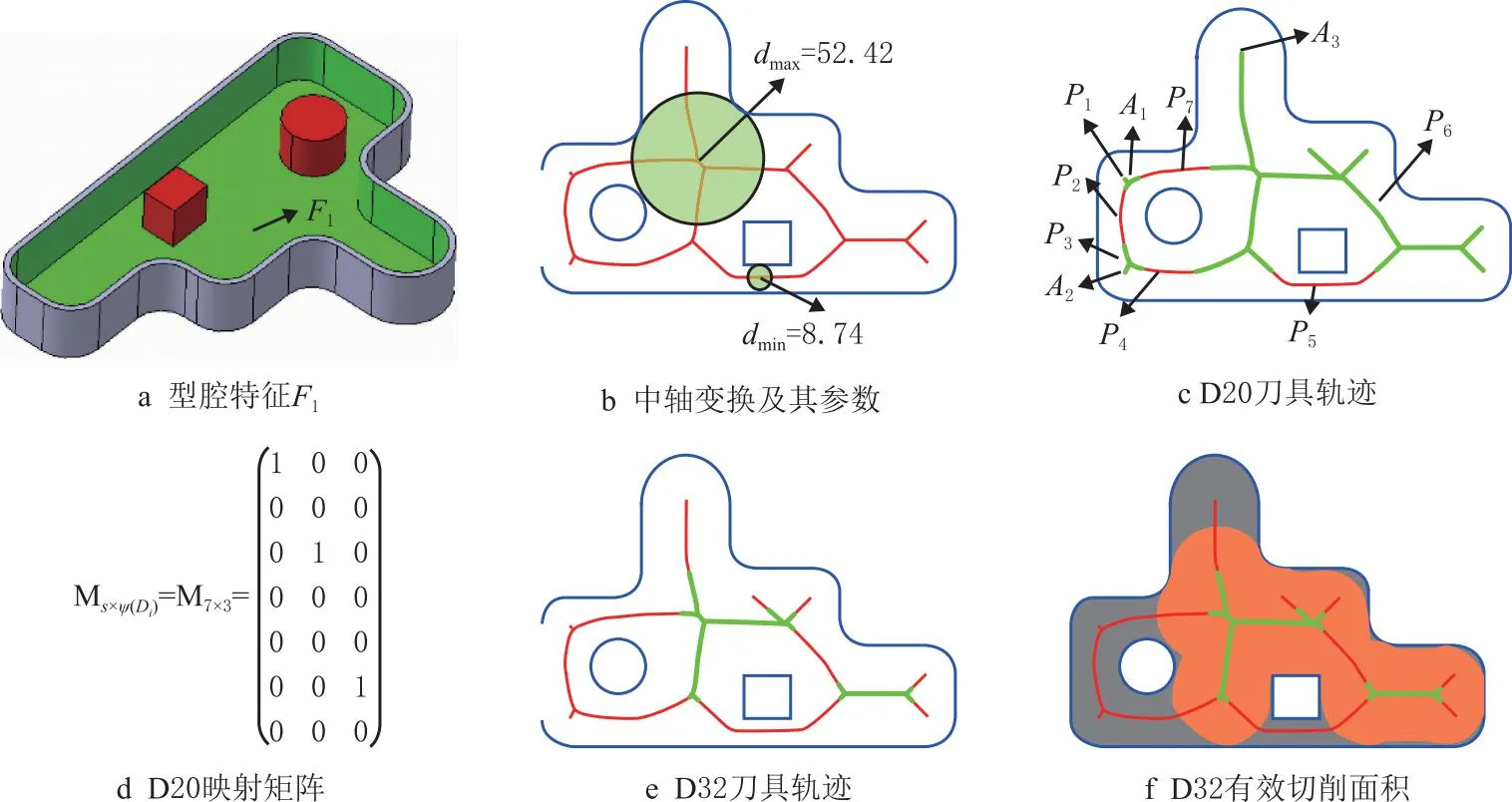
5.2 粗加工刀具序列优化决策实例
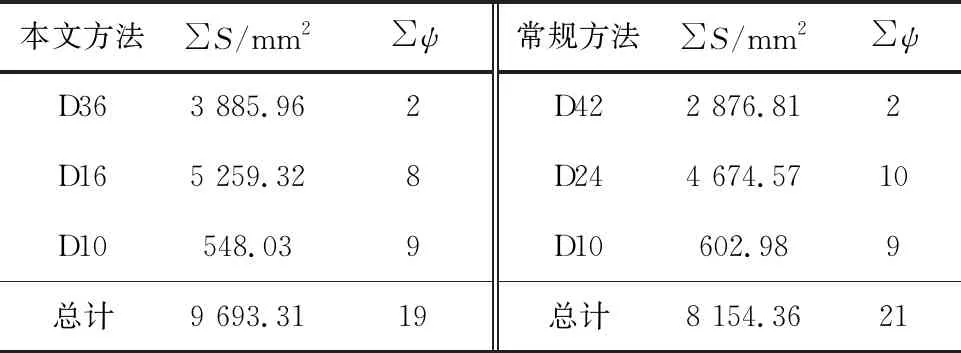
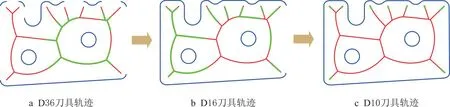
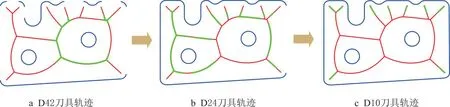
5.3 两种方法对比分析


5.4 有效性验证
6 结束语

