基于数字孪生的盾构机换刀机器人监控系统
殷光淼 ,朱国力+ ,谢 哲 ,王一新
(1.华中科技大学 机械科学与工程学院,湖北 武汉 430074;2.中铁工程装备集团有限公司,河南 郑州 450016)
0 引言
随着基础设施建设需求和地下空间开发力度的不断扩大,盾构机作为高度集成化的隧道施工设备,已广泛应用于城市轨道交通等工程建设中[1]。滚刀作为盾构机切削刀具,发生磨损时需要及时更换,而传统人工作业方式存在极大的安全隐患,与人工换刀作业相关的安全事故占比超过70%[2],机器人取代人工换刀成为必然趋势。盾构换刀机器人具有作业空间狭窄、末端负载大、多自由度和高定位精度、工作环境恶劣等特点:盾构机换刀舱空间狭小,舱门尺寸仅为600 mm×880 mm,舱门与刀盘距离仅为1.25 m,换刀机器人须在受限空间内精准移动至指定位置,完成机械臂伸缩、刀具拆卸、抓取返舱等动作,且末端抓取刀具重量高达250 Kg,整个换刀过程最大移动距离为3 m,整个操作过程易发生碰撞且对运动定位精度和刚度都有极高要求,机器人运动过程监控作为机器人服务的重要环节,对全方位了解设备运行状态,及时发现故障,保证设备安全性具有重要意义,但目前针对换刀机器人的研究集中于本体设计、轨迹规划等方面[3-4],关于换刀机器人监控技术的研究较少,且盾构换刀机器人受限于地下作业环境低光照、高湿度、泥土粉尘污染等恶劣环境因素制约,图像和视频信息难以监控设备状态,因此迫切需要开展换刀机器人监控技术研究,以全方位监控换刀作业流程,保证作业过程安全性。
对于其他应用场景的机器人可视化监控技术,国内外学者已开展大量研究:中国矿业大学王苏彧等[5]基于矿用隔爆型网络摄像仪组成视频监控系统,可将6路视频信号传输至地面控制点,实现煤巷掘进可视化。PAN等[6]研究了基于NI OPC的PLC-Labview通信技术,可同时获取多个喷涂机器人运动数据,实现对机器人喷涂轨迹的动态监控,但仍存在状态显示不直观、缺乏交互性等问题。数字孪生技术(Digital Twin, DT)通过数字化孪生模型动态映射物理实体的运动状态,实现物理空间与虚拟空间的互联互通[7],已经在工业装备监控运维领域得到广泛应用[8],方圆等[9]针对航空装配生产线设备运行状态可视化程度低的问题,提出了基于数字孪生技术的运行状态监控方法,并在某航空发动机外涵机匣装配生产线进行了验证。华中科技大学杜莹莹等[10]基于数字孪生技术构建工业机器人数字孪生体,实现了对于工业机器人的透明、实时可视化监控。
同时,越来越多的研究将虚拟现实(Virtual Reality, VR)、深度学习(Deep Learning, DL)等技术应用于数字孪生系统中:王文明等[11]将深度神经网络与数字孪生技术融合,不仅实现了海洋无隔水管作业过程监控与设备实时信息可视化,还可对故障信息进行有效诊断,提高修井的安全性与智能化水平。赵迪等[12]针对特种液压设备的液压缸活塞状态实时监控困难、安全性低等问题,基于数字孪生技术设计了液压缸在线监控系统,并基于BP(back propagation)神经网络构建液压缸活塞磨损程度预测模型,保证特种液压设备的安全性。西安科技大学张旭辉[13-14]团队就数字孪生技术在煤矿采掘设备中的应用开展了大量研究,如基于数字孪生技术提出了“人—信息—物理系统”的煤矿装备智能控制交互机制,实现地面虚拟掘进与井下实际掘进的深度融合,为煤矿开采提供可视化控制决策依据[15];针对井下高粉尘的恶劣工作环境导致劳动人员作业强度大的问题,将VR(virtual reality)技术应用于悬臂式掘进机的远程控制中,实现了虚实同步、人机协作的远程控制概念[16]。该团队的一系列工作对煤矿开采智能化的发展具有重要意义。
针对当前盾构换刀机器人受作业环境低光照、高污染等恶劣工况制约而缺乏有效监控方式的问题,本文设计了一种基于数字孪生技术的盾构机换刀机器人监控系统,该系统基于Unity3D平台构建与真实换刀机器人保持高度一致性的数字孪生体,基于BP神经网络构建末端执行器力学数据监测模型,可在机器人关节变量等实时数据驱动下映射真实运动状态,快速监测不同工况下末端执行器应力、形变数据。通过构建上述数字孪生系统保证盾构换刀操作过程安全性,优化故障的处理和决策能力,为盾构施工智能化发展作出一定贡献。
1 盾构机换刀机器人监控系统数字孪生框架
基于陶飞等[17]提出的数字孪生五维模型理论,结合盾构机换刀工程问题实际需求,盾构机换刀机器人监控系统由物体实体层、数据层、虚拟孪生层、应用层及各层之间的连接组成,如图1所示。

图1 盾构换刀数字孪生智能监控系统框架
1.1 物理实体层
物理实体层由真实存在的实体组成,是数字孪生系统的构成基础。盾构机换刀机器人监控系统中物理实体主要包括:刀盘、刀盘护盾、重载换刀机器人结构组件以及数据采集装置(如磁感应式位移传感器、角度编码器等)。其中:重载换刀机器人是完成换刀动作的主要执行机构,也是盾构机换刀机器人监控系统的主要监控对象;数据采集装置是获取孪生数据的途径,通过连接层可将实时数据传输至数据层。
1.2 数据层
数据的精准采集和高效传输是决定孪生系统实时性的关键因素[18]。盾构机换刀机器人监控系统数据层主要包括工艺设计参数和实时运行数据两个部分。前者主要包括换刀机器人各工件几何尺寸、装配关系以及刀盘、换刀机器人等结构之间的空间位置关系,通过上述数据基于三维建模软件可完成系统三维建模及虚拟孪生环境下的空间布局;也包括滚刀、末端执行器等零部件材料、各部件之间约束关系等,该部分数据是有限元模型建立的基础。后者是指换刀机器人执行换刀操作时的实时数据,包括数据采集装置获取的换刀机器人各个关节位移、速度、液压油缸压力等数据。数据层是整个数字孪生系统的驱动[19],为数字孪生系统起到基础感知作用。
1.3 虚拟孪生层
虚拟孪生层是基于虚拟仿真平台构建的物理实体数字化镜像。利用Soildworks等三维建模软件建立真实换刀机器人的三维几何模型;基于实际工况和约束条件构建换刀机器人有限元模型;在Unity3D开发平台下根据真实换刀系统的物理特征构建数字孪生体,并在孪生数据的驱动下实现对于物理空间运动的镜像映射。同时,有限元模型根据不同工况下的载荷输入,基于机器学习算法快速获取末端执行器力学响应,实时监控模型的力学响应数据,为盾构机换刀系统提供安全性保障。
1.4 应用层
应用层是基于虚拟孪生层,面向实际应用中的使用要求,通过智能算法及程序封装提供的相应服务和应用[20]。盾构机换刀数字孪生监控系统应用层由实时监控、数据面板显示、VR交互和力学监控4个模块构成。实时监控模块通过数字孪生体映射真实运动状态;数据面板显示模块将数据解析并显示在(User Interface,UI)交互界面中,增强系统可视化程度;力学监控模块基于机器学习算法快速获取末端执行器的应力形变数据,保证换刀操作的安全性,优化故障的处理能力;VR交互模块利用VR硬件设备与盾构机换刀系统实时交互,可用于盾构机操作过程演示与教学,提高系统沉浸性体验。
2 基于Unity3D的监控模型构建
Unity3D封装了多项软件开发工具包(Software Development Kit,SDK)且与VR硬件设备具有良好的兼容性,广泛应用于游戏开发、工业设计等领域,盾构机换刀机器人监控系统也采用Unity3D作为开发平台。为实现数字孪生系统与物理空间下的运动状态匹配,构建了运动学模型以耦合虚拟空间和真实物理空间;为实现全方位的监控效果,基于VR技术及全景漫游技术构建了数字孪生系统的UI交互系统,提高了监控系统交互能力及可视化效果。
2.1 换刀机器人运动学分析
换刀机器人作为盾构机换刀操作的主要执行机构,其机身姿态的实时监控对于提高换刀精度具有重要意义,通过换刀机器人运动学分析建立机身运动学方程,可用于描述任意时刻下机身末端执行器相对于基座标系的位置关系。
换刀机器人由多个移动副和转动副组成(图2a),采用Modified-DH法建立换刀机器人连杆坐标系,与Standrad-DH方法相比,该方法将坐标系建立在靠近基座一侧即连杆驱动轴上, 机器人各关节可由连杆夹角θi、连杆距离di、连杆长度ai,连杆扭角αi四个参数组成,Modified-DH坐标系下的转动关节示意图及连杆坐标系各参数定义分别如图3和表1所示,换刀机器人连杆坐标系如图2b所示。

表1 连杆坐标系参数定义表

图2 换刀机器人连杆坐标系建立
在Modify-DH法中,相邻两连杆i-1与i的坐标系之间的变换关系可表示为以下4个步骤:
(1)绕xi-1轴旋转αi-1角,使得zi-1轴与zi轴同向。
(2)沿xi-1轴平移距离ai-1,使得zi-1轴与zi轴共线。
(3)沿zi-1轴平移距离di,使连杆i-1的坐标系原点与连杆i的坐标系原点重合,zi-1轴与zi轴重合,xi-1轴与xi轴共面。
(4)绕zi-1轴旋转θi角,使xi-1轴与xi轴重合。
经过上述变换,可得到在Modified-DH坐标系下,连杆i的坐标系相对于连杆i-1的坐标系的坐标变换矩阵,式中:Rot表示旋转齐次变换,Rot(x,α)表示绕x轴旋转α角度,Trans表示平移齐次变换,Trans(Δx,Δy,Δz)表示沿坐标轴分别平移对应的变化量,c,s分别代表cos,sin:
Ai=Rot(xi-1,αi-1)Trans(ai-1,0,0)
Trans(0,0,di)Rot(zi,θi)=
图3所示的盾构机换刀机器人DH参数表如表2所示。
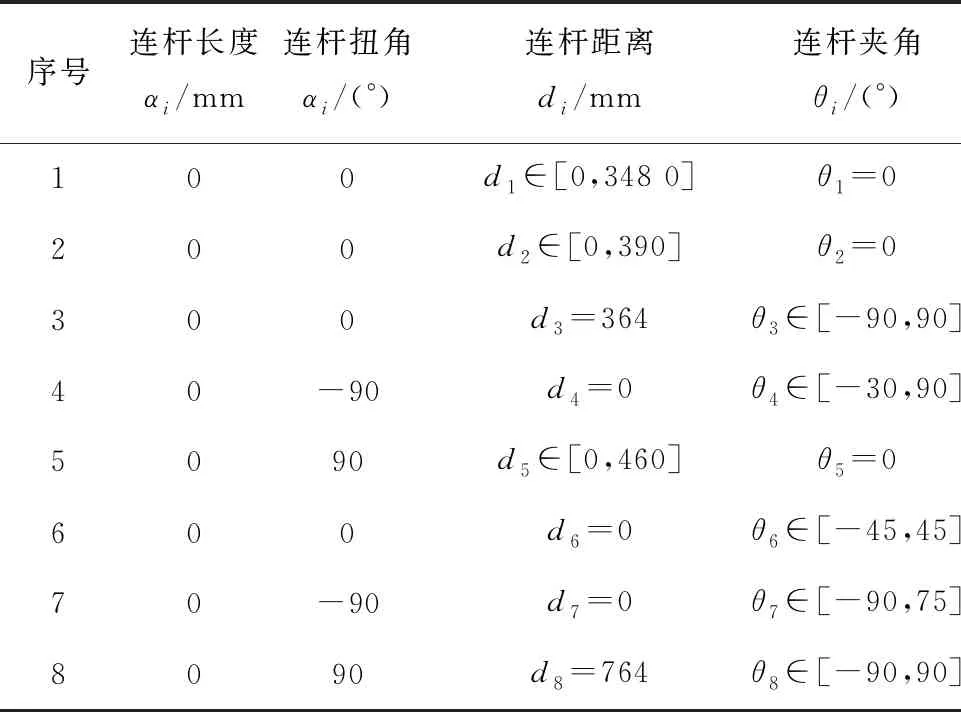
表2 盾构换刀机器人DH参数表
根据表2数据,对于图2b所建立的换刀机器人Modify-DH坐标系,相邻连杆之间的位姿矩阵Ai可分别计算如下:
A1=Trans(0,0,d1),
A2=Trans(0,0,d2),
A3=Rot(Z2,θ3)Trans(0,0,d3),
A4=Rot(Z3,θ4)Rot(X4,α4),
A5=Trans(0,0,d5)Rot(X5,α5),
A6=Rot(Z5,θ6),
A7=Rot(Z6,θ7)Rot(X7,α7),
A8=Rot(Z7,θ8)Trans(0,0,d8)Rot(X8,α8)。
(2)
则换刀机器人末端坐标系相对于基础坐标系的位姿矩阵,即换刀机器人的运动学方程为:
(3)
式中各项具体表达形式如下,为简化公式表示形式,式中ci=cosθi,si=sinθi。
nx=c8(c7(c6(c3c4-s3s4)-s6(c3s4+c4s3))-
s7(c6(c3s4+c4s3)+s6(c3c4-s3s4))),
ny=c8(c7(c6(c3s4+c4s3)+s6(c3c4-s3s4))+
s7(c6(c3c4-s3s4)-s6(c3c4+c4s3))),
nz=-s8,
ox=-c7(c6(c3s4+c4s3)+s6(c3c4-s3s4))-
s7(c6(c3c4-s3s4)-s6(c3s4+c4s3)),
oy=c7(c6(c3s4-s3s4)-s6(c3s4+c4s3))-
s7(c6(c3s4+c4s3)+s6(c3c4-s3s4)),
oz=0,
ax=s8(c7(c6(c3c4-s3s4)-s6(c3s4+c4s3))-
s7(c6(c3s4+c4s3)+s6(c3c4-s3s4))),
ay=s8(c7(c6(c3s4+c4s3)+s6(c3c4-s3s4))+
s7(c6(c3c4-s3s4)-s6(c3s4+c4s3))),
az=c8,
px=-d5(c3s4+c4s3)-d8(c7(c6(c3s4+c4s3)+
s6(c3c4-s3s4))+s7(c6(c3c4-s3s4)-
s6(c3s4+c4s3))),
py=d5(c3c4-s3s4)+d8(c7(c6(c3c4-s3s4)-
s6(c3s4+c4s3))-s7(c6(c3s4+c4s3)+
s6(c3c4-s3s4))),
pz=d1+d2+d3。
(4)
根据式(4)所建立的运动学方程,结合机器人各关节DH参数,基于数据采集装置所采集到的实时关节变量数据,即移动关节的连杆距离和转动关节的连杆夹角,计算出该时刻换刀机器人末端执行器的位置和姿态并映射至孪生系统中,达到“数据驱动、虚实同步”的孪生效果。
2.2 可视化交互系统
根据物理空间下各部件尺寸、配合关系、工艺等数据建立三维模型,经模型减面优化、渲染贴图、格式转换后导入Unity3D,添加关节组件、刚体特性组件等物理特性;利用MySQL建立关系型数据库,基于Socket通讯将实时数据传输至Unity3D,并利用C#语言编写脚本解析字符串数据,基于式(4)运动学方程将实际运动数据传输至虚拟系统中,实现虚实场景的动态连接。为实现全方位监控效果,盾构机换刀机器人监控系统还设计了全景漫游系统和基于虚拟现实技术的VR交互系统。
(1) 全景漫游系统 全景漫游是指以第一人称视角全方位感受产品和空间的技术,用户可通过PC外设在自由控制虚拟场景下的观测位置。盾构机换刀机器人监控系统基于C#语言开发UI交互脚本,通过监听键盘方向键及鼠标滚轮,分别对应改变用户的观测位置和观测角度,当监听脚本被触发后,改变Unity下虚拟相机的Transform组件的位姿坐标或视野角(Field of View,FOV)实现全景漫游。
(2) VR交互系统 虚拟现实技术通过VR硬件设备呈现出逼真的三维仿真环境,使用户产生身临其境的交互式视景仿真效果:将HTC VIVE Pro2硬件设备与PC端连接,在Unity3D中导入Steam VR SDK作为虚拟现实系统开发平台构建VR环境并配置手柄按钮,实现视角切换、手柄UI射线交互等功能,实现VR环境下的沉浸式交互。可视化监控系统的构建流程如图4所示。
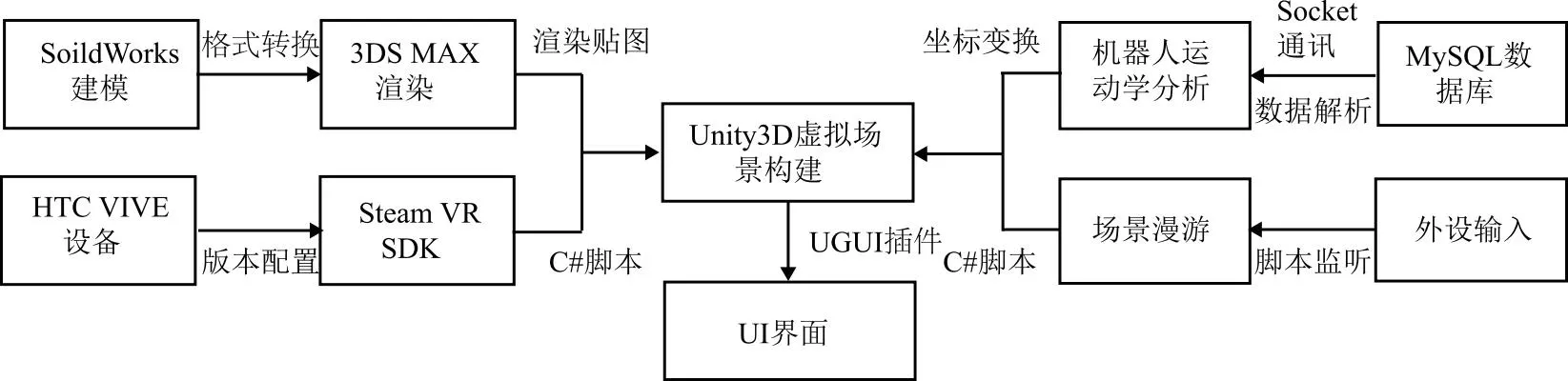
图4 可视化监控系统构建流程
3 基于BP神经网络的力学监控模型构建
在换刀机器人执行滚刀抓取动作过程中,实时监控末端执行器关键零部件的力学响应数据对保证系统安全性,提高监控系统智能化水平具有重要意义。但传统基于有限元仿真软件(如ANSYS,ABAQUS)的方式都需要经历前处理、求解计算、后处理的过程,存在分析时间长、难以满足数字孪生高实时性要求的问题。因此,本文基于不同工况下有限元仿真输出建立神经网络模型,在满足精度要求的前提下大幅提高仿真速度,快速获取末端执行器的应力和位移数据。
3.1 有限元仿真前处理
换刀机器人末端执行器基本结构如图5a所示,其中液压缸1、3为两个双作用液压缸,液压缸2为单作用液压缸,夹持手抓1由两个完全相同的零件组成。实际抓取时,液压缸2控制夹持手抓整体沿导轨方向上下移动至指定位置后,伸出端可视为固定约束,双作用液压缸1、3收缩带动夹持手抓1完成抓取动作,抓取过程的外载主要来自滚刀重力及液压油缸1,3的拉力。
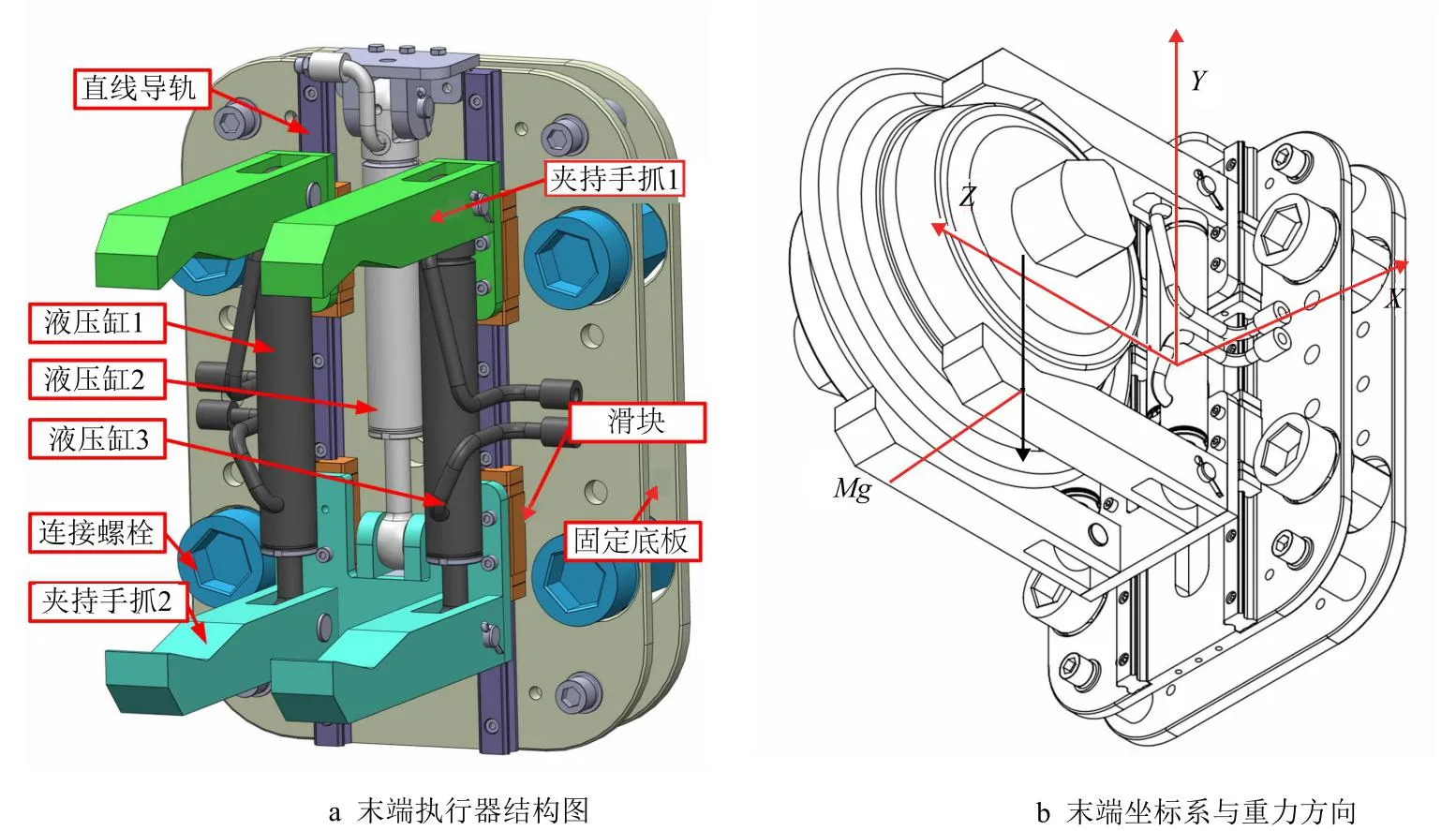
图5 末端执行器结构及末端坐标系
(1)液压油缸拉力范围计算
液压油缸压力计算公式如下:
F=βPS=βP(R2-r2)。
(5)
式中:β表示液压缸负载率,一般取0.8;P为液压压强,换刀机器人液压油压强范围为0~21MPa;R,r分别表示液压缸内壁半径及活塞杆半径,分别为50 mm和25 mm;计算可得液压缸最大拉力为25373.71 N。
(2)滚刀重力分解
实际抓取时滚刀重力方向始终竖直向下,末端坐标系的空间位姿随机器人位姿变化而改变(图5b),不同工况下进行有限元分析时都需要在仿真软件中调整末端夹具的位置,需耗费大量时间,故采用相对运动方式,将该问题转换为末端坐标系固定,重力矢量沿末端坐标系旋转。以末端坐标系Y轴与重力矢量方向相反 (图5b)为起始状态,此时重力矢量的坐标为:
(6)
当末端坐标系位置改变时,重力矢量在末端坐标系下的位置发生改变,可看作初始重力矢量(式(6))分别绕末端坐标系X,Y,Z三轴旋转固定角度得到,设定3个旋转角分别为:α,β,γ,分别对应图2a换刀机器人关节示意图中旋转关节6,7,8的连杆夹角θi,绕3个轴的旋转矩阵分别为:
(7)
重力矢量的旋转矩阵:
Mxyz=Rot(x)Rot(y)Rot(z)。
(8)
旋转后的重力坐标:
(9)
根据表2中连杆夹角的可行域范围,可分别计算3个方向加速度可行域:
ax∈[0,g]=[0,9806.6mm/s2],
ay∈[-g,0.996g]=[-9806.6mm/s2,9473.2mm/s2],
az∈[-g,g]=[-9806.mm/s2,9806.6mm/s2]。
(10)
汇总有限元分析的前处理模块相关数据,结果如表3所示。
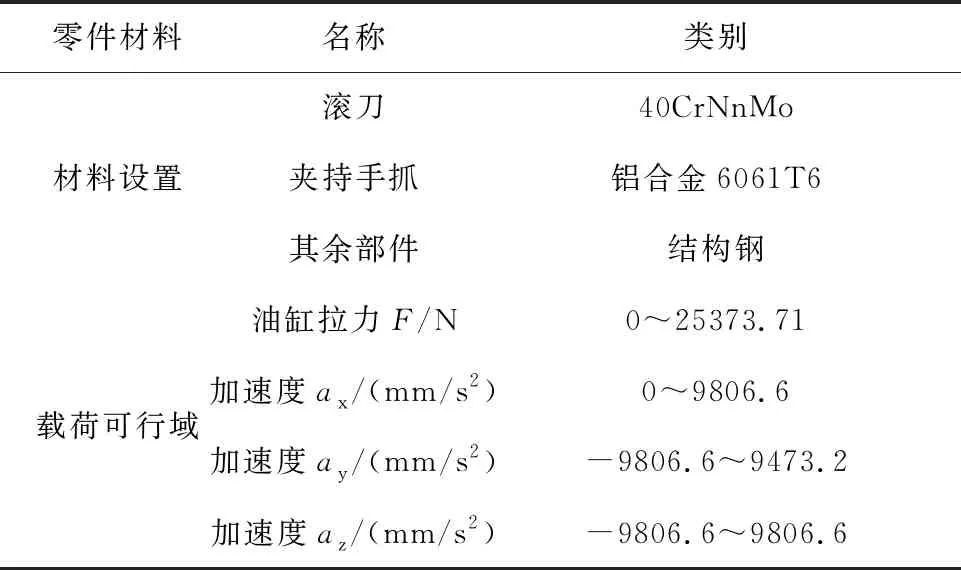
表3 零件材料及载荷可行域
3.2 零部件相关性分析
由于换刀机器人结构复杂,零件较多,基于参数相关性分析找出受输入影响较大的零件,并以此为分析对象建立力学回归模型。换刀机器人末端执行器液压缸、直线导轨均为标准件,故监控对象主要是结构中的非标准件(图5a 夹持手抓1、夹持手抓2)。
ANSYS相关参数系统(Parameters Correlation)是一种基于斯皮尔曼秩相关分析的方法,通过分析输入参数对每个输出参数的相关性和相对权重获取参数敏感性响应面,在输入参数可行域内基于拉丁超立方抽样(Latin Hypercube Sampling,LHS)生成样本执行仿真计算,并通过图表形式直观显示输入参数和输出参数之间的关系,用秩相关系数作为相关参数,即利用两变量的秩次大小作相关性分析。与常用的积差相关系数法相比,该方法对原始变量的分布不做要求,属于非参数统计方法,其数值介于[-1,1],正负代表参数相关的方向,当数值为0时,两变量完全无关。本文相关性分析的输入参数为油缸拉力F,加速度ax,加速度ay,加速度az,输入参数可行域如表3所示,输出参数为夹持手抓1、夹持手抓2的最大应力和最大位移,在输入范围内取100组样本点,最终得到的线性相关矩阵图如图6所示。
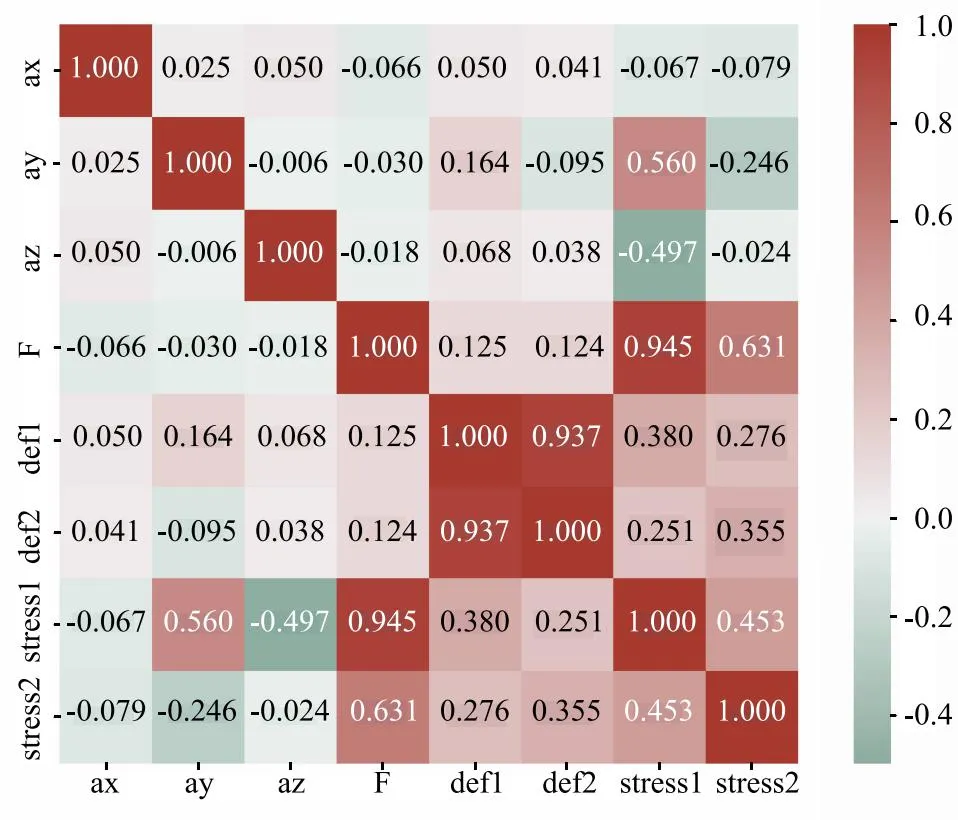
图6 有限元仿真输入输出参数线性相关矩阵
图6中def,stress分别对应夹持手抓的应力和位移输出,从图示结果可以看出,夹持手抓位移与输入参数相关性均较小,且夹持手抓1位移受输入参数影响大于夹持手抓2;夹持手抓应力与加速度相关性较小,但与油缸拉力相关性较强,且夹持手抓1与输入参数相关性强于夹持手抓2,因此选取夹持手抓1作为力学回归模型的分析对象。
3.3 表面节点数据集获取
图形学中通过模型表面特征点表征三维模型形状是常用的三维模型数字量化方法,为了数值化有限元模型的分析结果,拟选取有限元网格划分后的表面节点作为模型特征点,导出其力学响应数据作为神经网络回归模型的数据集。因为末端执行器夹持手抓并非规则几何体,神经网络模型的建立对模型本身节点个数并无要求,所以采用划分效率更高,几何通用性更强的四面体网格划分方式。将末端执行器三维模型简化后建立有限元模型并划分网格,单次输出夹持手抓1表面节点个数为3 380个。
在表3所示的输入参数可行域范围内,采用蒙特卡洛法(Monte Carlo method)生成300组样本数据,基于ANSYS APDL编写自动化仿真脚本,并将结果以txt文件保存至根目录下,最后Python读取根目录下的300个txt文件组成神经网络训练数据集,数据集样本总个数为1 014 000。
3.4 BP神经网络建立与优化
BP神经网络是一种按照误差逆向传播算法训练的多层前馈神经网络,是应用最广泛的神经网络模型之一。本节构建的末端执行器夹持手抓1的力学回归模型也采用BP神经网络建立,输入参数包括沿末端坐标系3个方向的加速度,油缸拉力及表面节点坐标,输出参数包括节点应力及节点位移。
Input=[x,y,z,F,ax,ay,az]
Output=[deformation,stress]。
(11)
因输入输出维度与神经网络数据集个数差异过大,通过传统确定隐藏层个数及层数的经验公式确定的神经网络结构拟合效果难以满足要求,需增大隐藏层节点个数,增加参数量[21]优化拟合效果,采用均方误差(MSE)作为神经网络损失函数,表4比较了不同层数及隐藏层节点个数下,训练500轮次(Epoch)后神经网络MSE结果值。
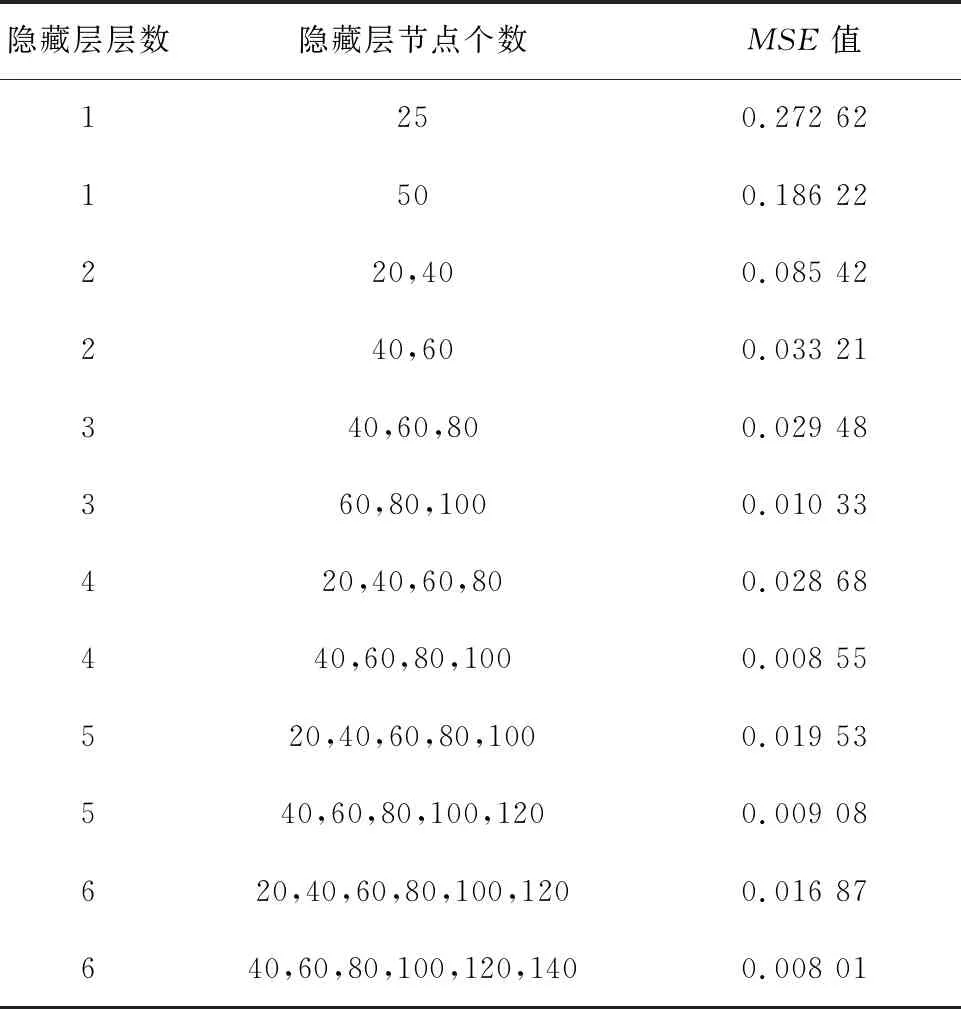
表4 隐藏层层数和节点数对BP网络的影响
如表4所示,增加隐藏层层数和隐藏层节点数均可提高神经网络拟合效果,但就隐藏层层数而言,当隐藏层层数超过3层后,对拟合效果的提升并不明显,且增加层数会显著增加计算机运行负载,增大网络训练时间;相较而言,层数不变时,增加隐藏层神经元个数对MSE结果的影响更为显著。经多次测试后,本回归模型选择的神经网络结构为5层BP神经网络(3隐藏层),隐藏层节点个数分别为100,150,50,如图7所示。

图7 三层BP神经网络结构
通常来说,样本数量越多,神经网络越可以更好地学习数据的特征和模式,模型的准确性和泛化能力也会越好,但数据集过大将导致训练时间过长和系统内存不足,加重计算机负担等问题。当神经网络精度满足要求时,可以通过随机抽样、分层抽样等方法减少样本数量,从而减少训练时间。
本文从数据集1 014 000组样本中随机选取300 000组数据组成新的数据集,并按照90:9:1划分训练集,测试集和验证集。采用均值方差标准化的方式对数据预处理:
(12)
为了避免梯度消失和神经元“死亡”的问题,选择LeakyReLU函数作为激活函数:
(13)
在神经网络训练过程中学习率过大容易震荡,学习率过小又会减缓收敛速度,因此采用变学习率方式,学习率初始值为0.01,每100个Epoch,学习率折半。学习率随训练次数的变化曲线如图8所示。设置训练轮次为800,随着训练次数的增加,MSE逐渐减小至0.005并收敛,图9展示了100~800轮次训练过程损失函数变化情况。

图8 学习率变化曲线

图9 BP神经网络误差收敛曲线
神经网络输出结果与标签结果作散点图标准化对比常用于验证神经网络的可靠性[22],以验证集3 000个样本为验证对象,将神经网络预测的应力和位移结果分别与有限元分析结果进行对比,结果如图10所示(散点图中数据为式(12)标准化后的输出结果)。
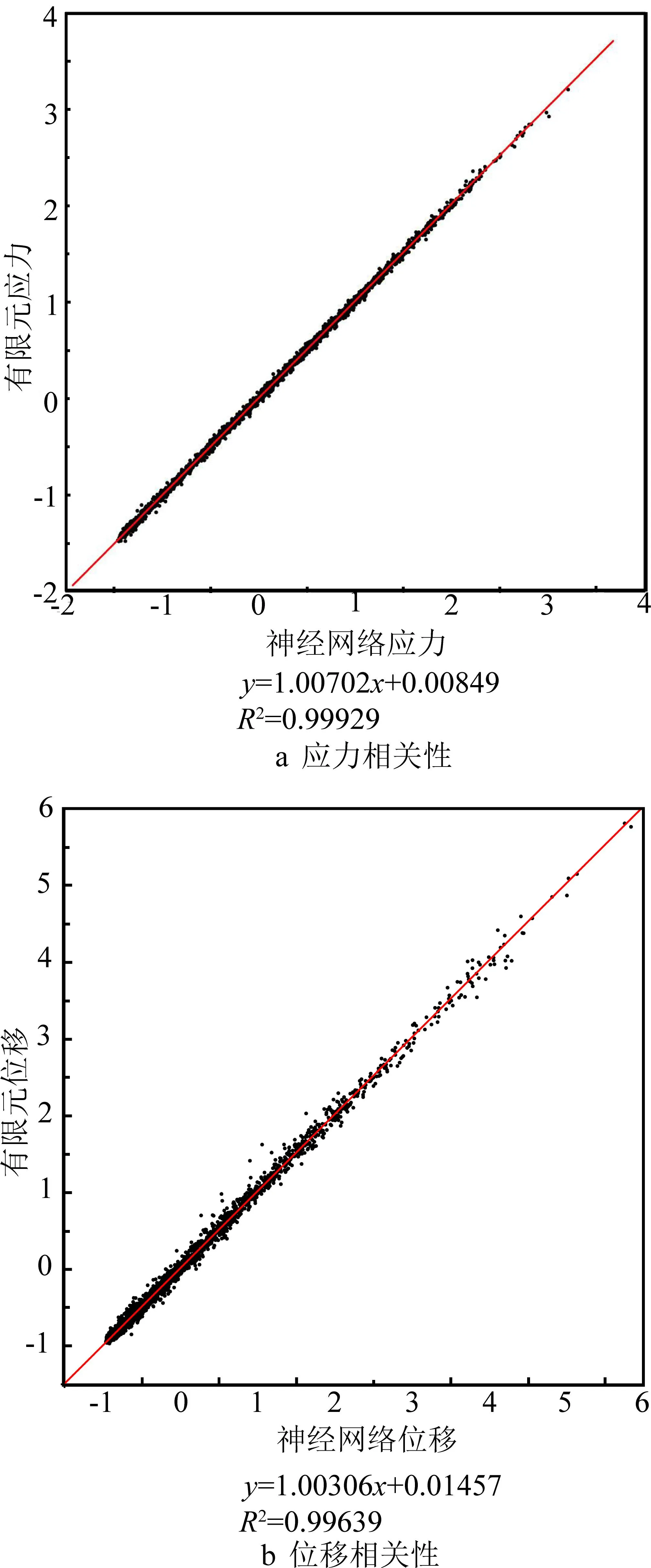
图10 神经网络预测结果与ANSYS仿真结果对比
图10中应力和位移两个维度线性回归决定系数分别为0.999 29和0.996 39。和回归线斜率均接近于1,表明神经网络预测结果与有限元仿真结果的高度一致性,证明本节所建立的神经网络对于力学响应回归问题的有效性。
以验证集样本为测试对象,将神经网络预测结果反标准化后与标签结果进行对比,得到位移和应力误差如图11所示,二者标准差分别为0.025和0.6971,相对误差分布满足3原则,验证集标签中应力最大值为82.277 Mpa,位移最大值为4.262 1 mm,图中应力误差最大值为2.784 Mpa,位移最大误差值为0.124 mm(取误差绝对值),占比分别为3.383%和2.029%,故该神经网络的预测结果与有限元仿真结果误差在5%以内,满足数字孪生系统设计需求。
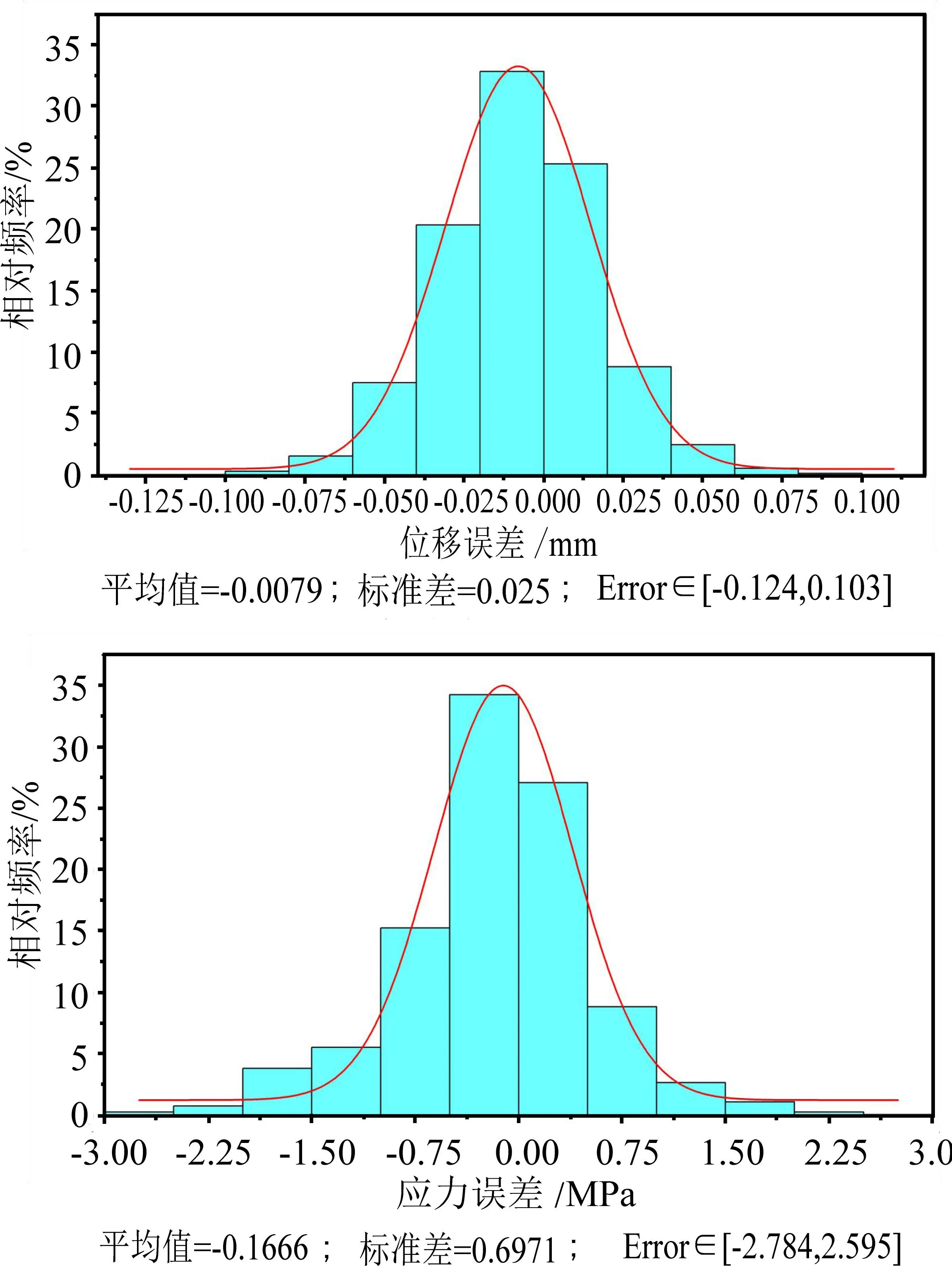
图11 神经网络预测结果误差分布
为进一步验证上述网络应用于手抓1全部节点的预测正确性,在表3所示的载荷可行域内随机选取一组工况,ax=4 647.850 mm/s2,ay=501.879 mm/s2,az=8 246.332 mm/s2,F=10 465.95 N。在该载荷下,将有限元仿真得到的3 380个节点的应力和位移与神经网络的输出结果进行对比,二者误差箱线图如图12所示。
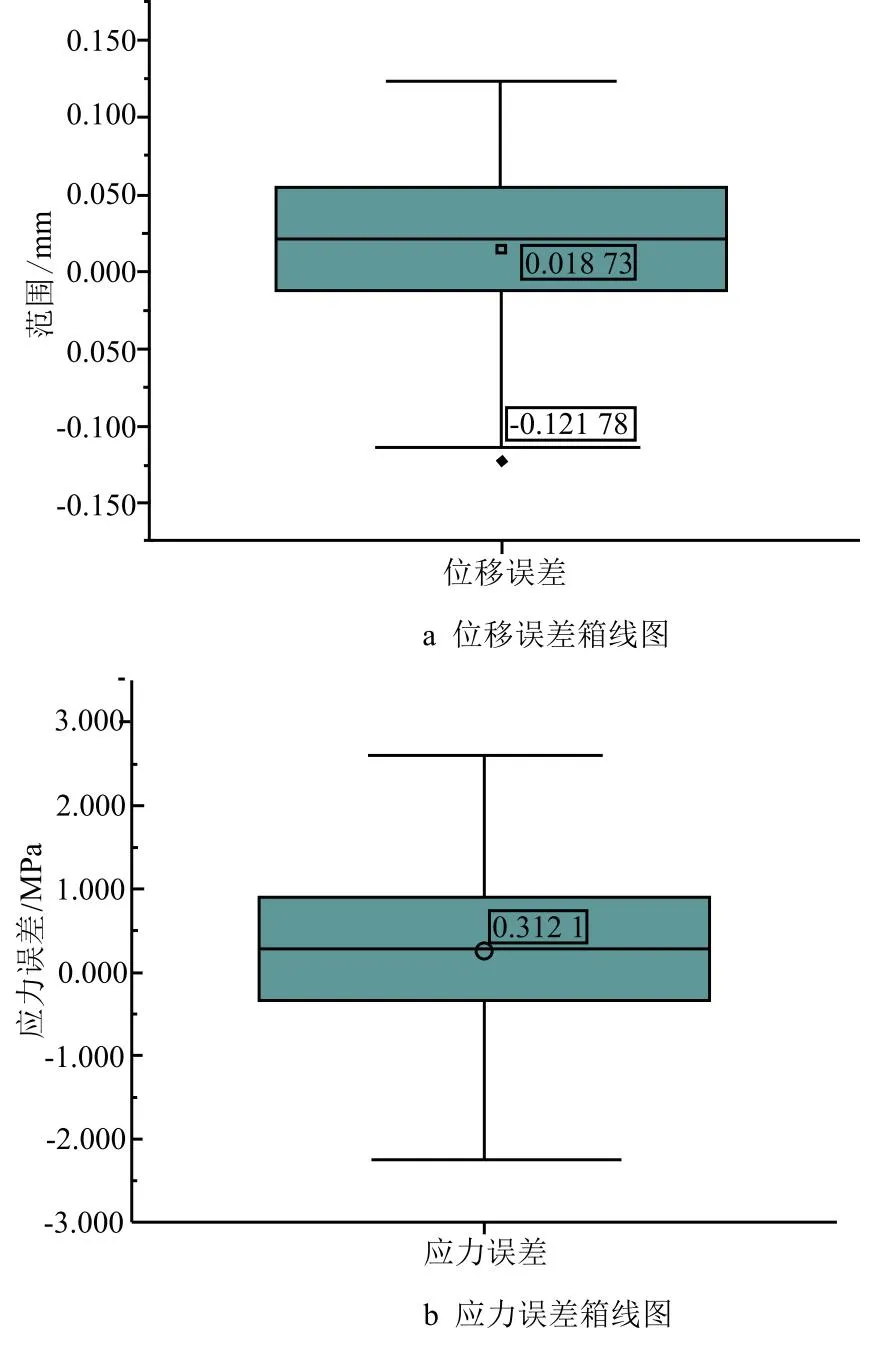
图12 单次输入下3380个节点误差分析
从图12可以看出,单次输入下抓手1上全部节点的位移和应力误差分布均符合一定偏态的正态分布,其中,位移误差均值为0.018 73 mm,存在一个离群值,但离群值范围满足图11误差分析中位移误差极限范围;应力误差均值为0.312 1 Mpa,无离群值。二者均满足前述的神经网络误差范围,证明所提出的方法的有效性。
3.5 基于open3d点云的云图实现
根据3.4节建立的神经网络虽然可以基于输入数据快速获取表面节点应力和位移,却无法实现ANSYS等有限元仿真软件的云图方式直观展示输出结果。点云作为一种对目标物体空间结构及表面特征描述的点集合,广泛应用于CAD建模、渲染等技术中,因此采用点云方式实现神经网络预测结果的云图展示。在点云中,每个点所包含的信息如下:
Point=(x,y,z,R,G,B)。
(14)
式中:前3项代表该点在空间坐标系下的坐标值,对应式(11)中神经网络输入中的节点坐标;后3项代表该点的颜色信息,R,G,B的值改变即可显示不同的颜色。对于模型表面每个节点空间坐标,基于前述建立的神经网络预测应力和位移,并根据结果大小分段赋予各点不同的颜色信息,实现云图展示。
但3.3节神经网络数据集获取过程中,单次工况下模型表面取点个数为3 380,若仅采用3 380个点作为夹持手抓模型的点云数据,形成的点云空洞较大影响观察效果,点云空洞填充算法虽然可以通过插值方法实现点云空洞修补,但插值计算过程需要消耗大量的时间,难以满足数字孪生系统实时性的要求,因此拟采用增加点的个数的方式减小点云空洞,通过ANSYS软件为建模对象划分更加致密的网格并获取表面节点坐标,以此作为神经网络输入参数,计算得到各点的应力和位移。
Open3d作为主流点云处理SDK,其封装了大量的点云处理算法并为Python提供了高效接口,而虚拟系统开发引擎Unity3D仅支持C#和JavaScript语言,难以实现点云效果。故力学监控系统采用Open3d编写点云处理程序,并在Unity编辑器中集成Python Scripting模块,数据库中的实时数据传输至Unity引擎后调用Pyhton点云代码实现力学监控效果,关于有限元云图效果的绘制流程如图13所示。

图13 虚拟实体中有限元云图绘制过程
4 实验结果与分析
为验证盾构机换刀机器人监控系统性能,以盾构换刀系统孪生体为基础构建模拟实验场景,通过串口测试工具模拟实际换刀机器人上位机发送孪生数据,虚拟样机与串口测试工具通过Socket通讯方式建立连接,数据发送频率为30 Hz,Unity虚拟样机作为客户端,虚拟系统的硬件设备配置如表5所示。

表5 仿真环境硬件配置
图14a为盾构机换刀机器人监控系统主界面,可通过界面上端UI交互按钮切换至VR环境、手动演示、数据驱动等多个模块。在数据驱动模块中,盾构换刀机器人在孪生数据驱动下与物理空间换刀机器人同步运动,通过页面左侧视角切换按钮可从不同角度观测换刀机器人移动,也可通过全景漫游功能,通过键盘方向键和鼠标滚轮自由切换观测视角和位置。页面右侧数据显示面板可实时显示由物理实体传输的实时数据,实现对于盾构换刀操作的可视化实时监控。在VR环境模块下,可佩戴硬件设备在虚拟现实环境下观测换刀机器人运动状态,同时可利用手柄与虚拟环境下的UI交互。

图14 盾构换刀数字孪生系统操作平台
图15为盾构机换刀机器人监控系统运行时的CPU性能分析图,通过系统运行时的帧率(Frame Pre Second,FPS)变化反映系统的流畅程度。帧率大小影响视觉上画面的平滑度,帧率过小(<15 FPS),就能够感到画面明显卡顿,帧率越大,在屏幕上显示的画面越平滑,一般认为帧率稳定在15 FPS~75 FPS范围内系统运营流畅。图15中阶段一为漫游系统测试,通过外设交互不断改变场景观测相机位置,帧率产生波动但仍保持在30 FPS以内较为稳定;阶段二为力学监控测试,该阶段脚本(Scripts)占用率显著升高,出现峰值帧率接近15 FPS的情况,但大部分时段帧率仍在15 FPS以内;阶段三为实时监控阶段,无UI交互时系统帧率稳定在60 FPS附近;阶段四为VR监控阶段,该阶段内渲染(Rendering)占用率显著升高,但系统帧率仍保持在15 FPS以内。综上,盾构换刀数字孪生系统虚拟样机运营流畅无卡顿,满足使用要求。
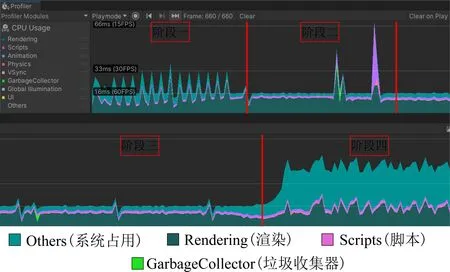
图15 运行时CPU占用分析
图16所示为相同输入下,ANSYS有限元软件的仿真结果和数字孪生系统应力监控结果对比。从图示结果可以看出,数字孪生系统的应力监控和位移监控云图分布情况与ANSYS结果基本一致,图16所示结果中,神经网络预测结果和有限元仿真结果的夹持手抓1最大应力误差为0.707 Mpa,最大位移误差为 0.004 8 mm,均在图11所示的误差范围内。仿真速度方面,根据ANSYS Solution Information所记录的仿真时间,ANSYS仿真用时69.1 s,而对力学监控模块采用time()函数对神经网络仿真计时,单次仿真时间在20 ms左右,小于Unity引擎单组数据传输时间(33.3 ms),满足系统设计需求,相较于ANSYS有限元仿真速度得以大幅提高。
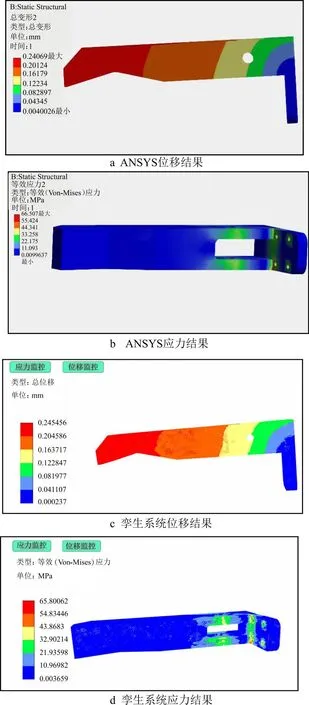
图16 ANSYS仿真与力学响应监控模块效果对比
5 结束语
针对当前盾构换刀机器人受作业环境低光照、高污染等恶劣工况制约而缺乏有效监控方式的问题引入数字孪生技术,本文提出一种基于数字孪生的盾构机换刀机器人监控系统,主要结论如下:
(1)设计了包括物理实体层、数据层、虚拟孪生层、应用层和各层之间的连接5部分的盾构机换刀机器人监控系统数字孪生框架。并基于Unity3D构建虚拟孪生体,通过实时数据采集与传输、换刀机器人正运动学和坐标变换耦合物理系统和虚拟系统,实现物理空间与虚拟空间的运动状态匹配,为盾构施工智能化提供了新的发展方向。
(2)基于BP神经网络构建了末端执行器力学数据监测模型,可实时获取末端执行器应力和位移数据。并通过数据验证所构建的神经网络应力和位移绝对误差分别为2.784 Mpa和 0.124 mm,单次仿真时间提升至20 ms左右,精度和实时性均满足设计要求。
(3)基于所构建的盾构机换刀机器人监控系统样机进行了实验测试,验证了盾构机换刀机器人监控系统可在可视化监控和力学响应监控方面的可行性,系统运行流畅,无明显延时,整体运行帧率在15 FPS以内,用户交互体验好。
综上,关于基于数字孪生的盾构机换刀机器人监控系统的研究是数字孪生技术在工程实践中的应用以及盾构技术智能化发展的案例,为盾构机换刀施工过程可视化提供了全新的解决方案,但根据数字孪生成熟度理论,目前关于盾构机换刀机器人监控系统的研究仍处于“以虚映实”阶段,且VR监测环境受硬件设备制约,适用场景受限。下一步将就基于虚拟系统的机器人控制基于虚拟系统的碰撞预测等方向展开研究,实现 “以虚控实”、“以虚预实”的高成熟度孪生系统。

