考虑最小尺寸控制的压力驱动柔顺机构拓扑优化设计

占金青 ,蒲圣鑫 ,王 啸 ,刘 敏+

(1. 华东交通大学 机电与车辆工程学院,江西 南昌 330013;2. 华东交通大学 载运工具与装备教育部重点实验室,江西 南昌 330013)

0 引言

柔顺机构是一种由自身柔性元件的弹性变形来实现能量传递、力或运动的整体式机构[1-2]。柔顺机构的驱动力可以分为两类:①与设计相关的载荷,如流体压力载荷;②与设计无关的载荷,如恒力载荷。压力驱动柔顺机构在人机交互、医疗康复和军事探测等领域具有广泛的应用前景[3-4]。拓扑优化方法[5-6]是柔顺机构设计方法之一,它能在给定的设计域、约束边界和输入、输出作用等条件下寻求机构最佳的机构构型,使得性能达到最优。在压力驱动柔顺机构拓扑优化过程中,流体压力作用边界不断地演变,引起设计相关的压力载荷的大小、位置和方向不断地变化。与恒力驱动相比,压力驱动柔顺机构拓扑优化设计面临着更多的困难。流体压力驱动柔顺机构拓扑优化设计研究引起越来越多学者的关注[7-8]。

HAMMER等[9]首先提出了一种流体压力载荷作用的连续体结构拓扑优化设计方法,利用等密度方法确定压力载荷边界。IBHADODE等[10]采用边界识别和载荷演化方法求解压力载荷边界,实现了承压结构拓扑优化设计。SIGMUND等[11]将空相结构视为不可压缩的静压流体,采用位移-压力混合有限元方法计算压力载荷,进行承压结构拓扑优化设计。LU等[12]提出一种基于移动等值面阈值法和位移-压力混合有限元法的压力驱动柔顺机构拓优化设计方法。PANGANIBAN等[13]采用基于位移的非协调有限元法进行流体压力驱动柔顺机构拓扑优化设计。DE SOUZA等[14]提出一种基于混合位移-压力有限元方法和投影技术的压力驱动柔顺机构拓扑优化设计方法。PICELLI等[15]采用水平集方法计算流体压力载荷场,建立了压力载荷作用的结构拓扑优化模型。KUMAR等[16]采用达西定律进行压力驱动柔顺机构拓扑优化设计,并扩展到三维结构设计问题中[17]。上述关于压力驱动柔顺机构拓扑优化设计研究没有考虑制造工艺要求,设计的压力驱动柔顺机构构型容易出现类铰链结构,导致难以加工制造。因此,需要考虑最小尺寸控制进行压力驱动柔顺机构拓扑优化设计,使得机构的最小特征尺寸满足加工工艺要求。

最小尺寸控制是为了满足压力驱动柔顺机构加工工艺要求必须考虑的因素,其目的在于使拓扑优化设计的压力驱动柔顺机构最小特征尺寸足够大。目前,考虑最小尺寸控制的拓扑优化设计研究主要集中在恒力驱动柔顺机构设计问题。SIGMUND[18]采用基于图形学中侵蚀、中间和膨胀算子的映射方法进行考虑最小尺寸控制的柔顺机构拓扑优化设计,获得的机构最小特征尺寸得到控制,但是每次迭代进行多次有限元分析。XIA等[19]通过施加边界到骨架的距离约束,实现了基于最小尺寸控制的柔顺机构拓扑优化设计。ZHOU等[20]提出一种基于几何约束的柔顺机构拓扑优化设计方法,以控制实相和空相结构最小尺寸。荣见华等[21]引入光滑Heaviside映射和修改的光滑Heaviside映射,建立了实相和空相结构最小尺寸控制的结构拓扑优化模型。占金青等[22]提出一种考虑混合约束的柔顺机构拓扑优化设计方法,获得的柔顺机构最大应力和最小尺寸得到控制。LIU[23]提出一种基于水平集的分段尺寸控制拓扑优化方法,能够达到分段尺寸控制效果。ZHANG等[24]提出一种基于结构骨架的柔顺机构拓扑优化设计方法,以控制结构的最大尺寸和最小尺寸。YAN等[25]采用浮动投影拓扑优化方法进行基于最小尺寸控制的柔顺机构设计。综上所述,基于最小尺寸控制的拓扑优化获得的柔顺机构最小特征尺寸能够得到有效地控制,但是仅涉及恒力驱动柔顺机构设计问题。考虑最小尺寸控制的压力驱动柔顺机构拓扑优化设计研究尚未见相关报道。

因此,本文提出一种考虑最小尺寸控制的压力驱动柔顺机构拓扑优化设计方法。采用达西定律与排水项相结合求解流体压力载荷,利用Otsu算法和拓扑细化算法提取柔顺机构的骨架特征,从而构建最小特征尺寸控制,建立考虑最小尺寸控制的压力驱动柔顺机构拓扑优化模型,采用移动渐近线算法进行优化问题求解。

1 流体压力载荷求解

目前,设计相关的流体压力载荷计算方法主要有边界识别和水平集方法。边界识别方法基于预先给定的密度阈值识别等密度曲线或曲面(压力载荷边界),可能形成“孤岛”,导致无法施加有效的压力载荷;水平集方法使用隐式边界描述压力载荷,但其计算量庞大。上述两种方法通常未考虑流体压力荷载边界变化对灵敏度分析影响,导致目标函数和约束灵敏度分析不准确。达西定律和排水项通过隐式形式有效地表达流体压力载荷边界,可通过伴随方法求解出压力载荷灵敏度,且计算成本低[26]。因此,本文采用达西定律和排水项计算流体压力载荷。达西定律表示流体通量与压力梯度成正比,与流体粘度成反比,可以表示为

(1)

式中,q表示流体通量,μ表示流体粘度,k表示渗透率,ρe表示单元密度,∇p表示压力梯度。K(ρe)代表流量系数,表示流体通过多孔介质的能力。为了使得介于0(空相)和1(实体)之间中间密度单元的流量系数连续平缓过渡,采用Heaviside映射函数[27]惩罚流量系数

(2)

(3)

式中:kv和ks分别为空相的流量系数和实相的流量系数;ηk为阈值;βk为控制近似Heaviside函数斜率的参数。

为了得到整个设计域的压降分布,采用排水项求得实-空相界面处的局部压力梯度

Qdrain=-H(ρe)(p-pout)。

(4)

式中:Qdrain为排水量,H(ρe)为排水系数,p为压力场,pout为外部压力场。

与流量系数类似,采用平滑的Heaviside函数惩罚排水系数H(ρe):

(5)

式中:βh和ηh为可调参数;hs为实相的排水系数,它有效地控制所施加压力的穿透位置和深度

(6)

其中r为输入压力在穿透深度Δs处的比值。

根据式(4),可以将式(1)改写为。

∇q-Qdrain=0。

(7)

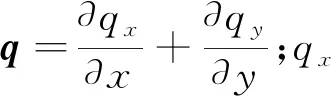
对于任一单元区域Ωe,式(7)的弱形式可表示为

(8)

式中:pe为压力场,Np=[N1,N2,N3,N4]为形函数矩阵,Bp=∇Np,qΓ为通过边界Γe的达西通量。

经组装后,式(8)可改写为:

Ap=f。

(9)

式中:A为整体流动矩阵,p为整体压力向量,f为整体载荷向量。

设定pout=0和qΓ=0,因此,与之相对应的负载向量f=0。由式(9),可以求得整体等效节点载荷向量F=-Hp。

单元转换矩阵He与单元等效节点载荷Fe的关系可表示为

(10)

式中Nu=[N1I,N2I,N3I,N4I],其中I是单位矩阵。

2 骨架提取及尺寸控制

采用变密度法进行压力驱动柔顺机构的拓扑优化设计,获得的机构构型容易出现大量灰度单元,导致无法准确提取图像特征。为了克服上述问题,采用自适应求解阈值的Otsu算法[28-29]进行灰度图像二值化处理。

2.1 Otsu算法

假设拓扑图的灰度级范围为(0,L-1),其中灰度级为i的单元有ni个,则设计域内的单元数目为:

(11)

Pi为第i灰度级出现的概率,即

(12)

设定分割阈值为k⊂[0,L-1],将拓扑构型灰度图划分为C0和C1两部分,分割后的单元灰度值可以表示为:

(13)

式中:C0为灰度图像的背景;C1为灰度图像的前景,即拓扑构型;x表示单元的坐标。灰度级小于k的像素点包含于C0中,反之包含于C1中。

用ω0和ω1分别表示C0和C1出现的概率:

(14)

C0和C1对应的灰度级类均值分别为μ0和μ1

(15)

式中,μ为灰度图像的平均灰度值

(16)

根据式(14)和式(15)可计算得到C0和C1方差分别为:

(17)

(18)

按照Otsu方法所遵循的类间方差准则,前景和背景的类间方差表示为

(19)

(20)

采用归一化方法对拓扑图灰度处理,可以使得拓扑图灰度级和单元密度一一对应。于是,对单元密度场进行分割处理,可以获得0/1分布的二值密度场

(21)

2.2 拓扑细化算法

拓扑细化算法是在不改变图像拓扑连接性关系前提下,经多次迭代细化,逐层地删去结构边界上简单点,最终获取单像素宽度的图像骨架。每次细化存在并行的两个图像处理过程,一个是删除东南边界点和西北角点,另外一个是删除西北边界点和东南角点。本文采用并行拓扑细化算法[30]提取二值密度场的骨架。

假设一个像素点p1,它的8邻域位置顺序如图1所示。在第一个图像处理过程中,若p1的邻域满足下列4个条件,将它从图像中删除,即像素值被赋予0值。

(22)

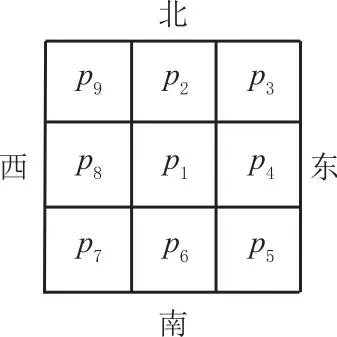
图1 像素点p1邻域示意图

其中:A(p1)为有序集合{p2,p3,p4,p5,p6,p7,p8,p9}中的01模式的数量;B(p1)为像素点p1的8邻域中非0像素点的数量,即

B(p1)=p2+p3+…+p8+p9。

(23)

在式(22)中,条件(a)B(p1)≥2保证p1点不是端点或孤立点,因为删除端点和孤立点是不合理的,B(p1)≤6保证p1点是一个边界点,而不是一个内部点;条件(b)A(p1)=1可以防止删除位于骨架线端点之间的像素点,可保证删除当前像素点后的连通性。若像素点p1的邻域不满足式(22)中的任一条件,则它得到保留。

在另一个图像处理过程中,若p1的邻域满足下列4个条件,将它从图像中删除;若p1的邻域不满足下列任一条件,则它得到保留。

(24)

2.3 最小尺寸控制

(25)

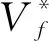
如果迭代开始施加最小尺寸控制,可能会造成拓扑优化结果出现早熟现象[21-22],从而不能获得最优的拓扑结构。为了避免这种现象出现,当单元物质密度灰度比例Mnd≤15%时,引入最小尺寸控制,Mnd表达式为:

(26)

3 考虑最小尺寸控制的压力驱动柔顺机构拓扑优化模型

3.1 拓扑优化模型

对于压力驱动柔顺机构拓扑优化设计问题,采用改进的固体各向同性材料惩罚模型(Solid Isotropic Material with Penalization, SIMP)[31-32]描述单元弹性模量与设计变量之间的关系,其表示为

(27)

式中:Ee为单元e的弹性模量;ξ为惩罚系数,ξ=3;E0为实体材料的弹性模量;Emin为空洞材料的弹性模量,Emin=10-6E0,以避免单元刚度矩阵奇异。

以压力驱动柔顺机构应变能最小化和互应变能最大化为优化目标,将结构体积和最小尺寸作为约束,建立考虑最小尺寸控制的压力驱动柔顺机构的拓扑优化模型为

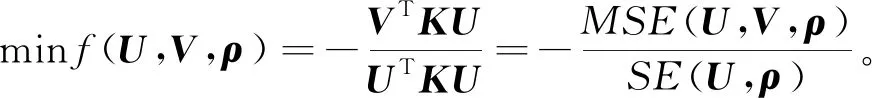
(Ⅰ)

Ap=0;

(Ⅱ)

KU=F=-Hp;

(Ⅲ)

KV=Fd;

(Ⅳ)

0≤ρe≤1 ,e=1,2,3…N。

(28)

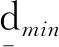
3.2 灵敏度分析

采用基于梯度的移动渐近线算法(Method of Moving Asymptotes,MMA)[30]求解压力驱动柔顺机构拓扑优化问题,因此需要计算优化目标和约束条件的灵敏度。

由式(28),目标函数的灵敏度求解为

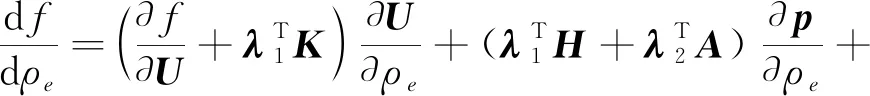
(29)

式中,λ1、λ2和λ3表示伴随变量向量,分别表示为

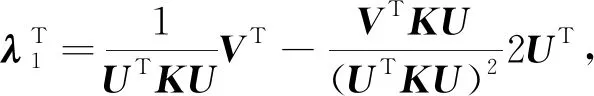
(30)

将式(30)代入式(29),目标函数灵敏度简化为

(31)

利用式(28)、式(29)和式(31),可求得

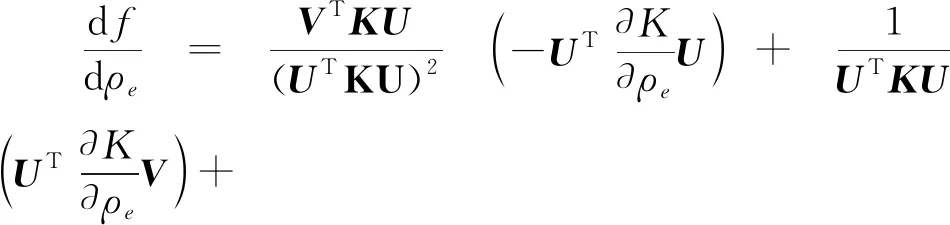
(32)

由式(28)中的约束(iv),求得体积约束的灵敏度为

(33)

由式(28)中的(Ⅳ)和式(25),求得最小尺寸约束的灵敏度为

(34)

3.3 优化流程

考虑最小尺寸控制的压力驱动柔顺机构拓扑优化设计方法流程如下:

步骤1设计域网格离散化,初始化设计参数;

步骤2进行有限元分析,计算目标函数与约束函数的灵敏度,采用密度过滤法修正单元密度;

步骤3通过密度投影获取二值场,并提取拓扑构型的骨架;

步骤4以最小控制尺寸dmin为直径扫掠步骤3所获取的骨架,确定最小尺寸控制域B(dmin);

步骤5根据灰度比例Mnd判断是否需要引入最小尺寸控制,是则转步骤6;反之,则转步骤7;

步骤6比较单元密度场和最小尺寸控制域,对不满足最小尺寸约束的区域填充材料,使机构构型满足最小尺寸控制;

步骤7对单元密度场进行Heaviside映射,获得清晰的单元物质密度场;

步骤8采用MMA算法更新设计变量;

步骤9判断是否满足收敛条件,若满足,结束运行;反之,返回步骤2。

4 数值算例

本章考虑最小尺寸控制的压力驱动柔顺机构拓扑优化设计方法通过MATLAB软件编程实现,采用反向器和夹持器两个数值算例验证该方法的有效性。所有算例中,实体材料的弹性模量E0为3×109Pa,泊松比υ为0.4,作用流体压力pin为1×105Pa,许用体积比g*为0.25,输出弹簧刚度Kout为5×104Nm-1。

4.1 反向器

反向器设计域、边界条件及输入输出作用如图2所示,设计域的尺寸为L×L=150 mm×150 mm,固定边界为左上端和左下端,将右端中点设定为输出端,左端面为流体压力载荷作用边界。考虑到反向器设计域对称性,取设计域的上半部分进行设计并离散为150×75个四节点单元。

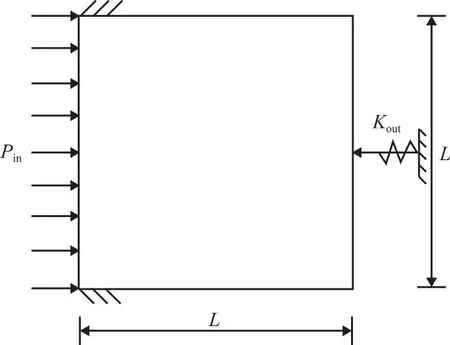
图2 反向器设计域

(1) 有、无最小尺寸控制比较

为了验证所提出方法的有效性,首先,进行无最小尺寸控制的流体压力驱动柔性反向器拓扑优化设计,优化结果如图3a所示,再次,取最小控制尺寸dmin=4进行考虑最小尺寸控制的流体压力驱动柔性反向器拓扑优化设计,优化结果如图3b所示,对应的反向器骨架如图4所示。由图3a可知,无最小尺寸控制拓扑优化获得的流体压力驱动反向器结构的最小特征尺寸较小,不易加工制造;且存在类铰链结构,类铰链导致应力集中、甚至疲劳破坏。与无最小尺寸控制的优化结果相比,考虑最小尺寸约束(dmin=4)的拓扑优化获得的反向器拓扑构型有所不同,结构最小特征尺寸很好地满足约束,便于加工制造;并且类铰链结构得到有效地抑制,如图3b所示。这表明提出的考虑最小尺寸控制的压力驱动柔顺机构拓扑优化方法是有效的。

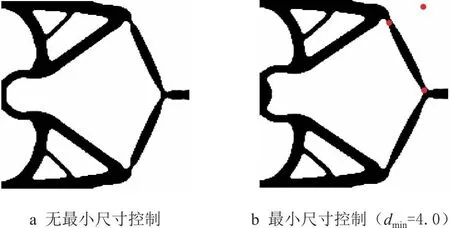
图3 有、无最小尺寸控制获得的反向器拓扑构型

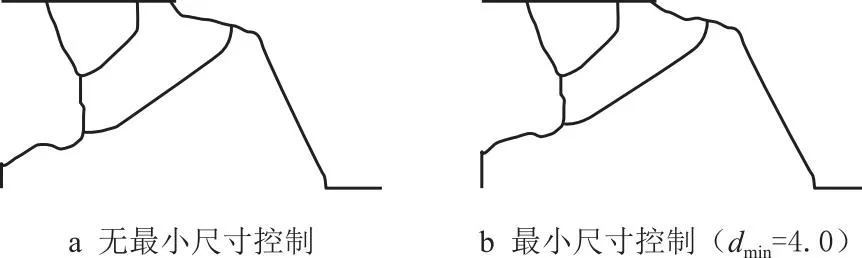
图4 有、无最小尺寸控制获得的反向器骨架

考虑最小尺寸控制的流体压力驱动柔性反向器拓扑优化设计的目标函数和体积比迭代曲线如图5所示,优化迭代初期出现振动,总体迭代过程平缓,经过100次迭代,目标函数和体积比趋于收敛。图6表示反向器灰度图像二值化的分割阈值迭代曲线,迭代过程中单元密度分布变化引起分割阈值不断变化;当迭代收敛时,分割阈值稳定于0.4353。与无尺寸约束优化结果相比,考虑最小尺寸控制的拓扑优化获得的目标函数f值有一定程度上减小,如表1所示。

表1 有、无最小尺寸控制的反向器拓扑优化结果

图5 考虑最小尺寸控制的反向器拓扑优化迭代历程

图6 分割阈值迭代过程(dmin=4)

(2) 不同最小控制尺寸

为了分析不同最小控制尺寸对拓扑优化结果影响规律,选取最小控制尺寸dmin分别为4.5,5.0,5.5,6.0进行流体压力驱动柔性反向器拓扑优化设计,获得反向器拓扑构型如图7所示。随着最小控制尺寸dmin增大,考虑最小尺寸控制的拓扑优化获得的压力驱动反向器拓扑构型发生变化,反向器结构的最小特征尺寸变得更大,均满足最小尺寸控制,类铰链结构均得到有效抑制;且目标函数f随之减小,即互应变能和应变能比值逐渐减小,如表2所示。

表2 不同最小控制尺寸的反向器拓扑优化结果

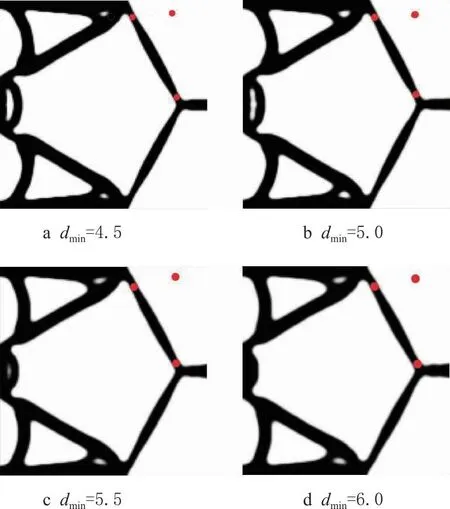
图7 不同最小控制尺寸获得的反向器拓扑构型(g*=0.25)

4.2 夹持器

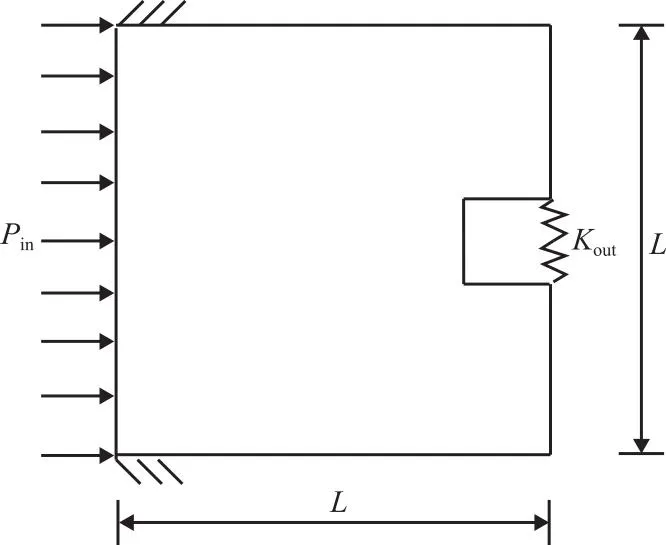
图8 夹持器设计域

(1)有、无最小尺寸控制

同样,考虑有、无最小尺寸控制进行流体压力驱动柔性夹持器拓扑优化设计,拓扑构型及骨架分别如图9和图10所示。与无最小尺寸控制的优化结果相比,考虑最小尺寸约束(dmin=4.5)的拓扑优化获得的夹持器拓扑构型有所不同,结构最小特征尺寸很好地满足约束,便于加工制造;并且类铰链结构得到有效地抑制,如图9所示。这也表明提出的考虑最小尺寸控制的压力驱动柔顺机构拓扑优化设计方法是有效的。

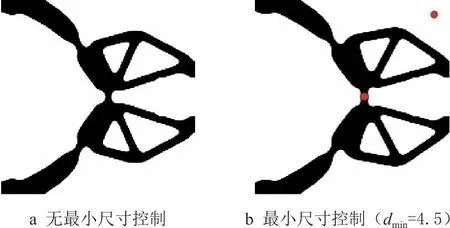
图9 有、无最小尺寸控制的夹持器拓扑构型及骨架

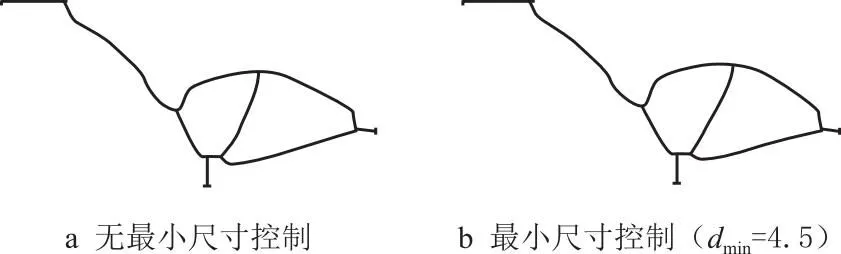
图10 有、无最小尺寸控制的夹持器骨架

考虑最小尺寸控制的流体压力驱动柔性夹持器拓扑优化设计的目标函数和体积比迭代曲线如图11所示,经过100次迭代,目标函数和体积比趋于收敛。图12表示夹持器灰度图像二值化的分割阈值迭代曲线,当迭代收敛时,分割阈值稳定于0.4353。与无尺寸约束优化结果相比,考虑最小尺寸控制的拓扑优化获得的目标函数f值有一定程度上减小,如表3所示。

表3 有、无最小尺寸控制的夹持器拓扑优化结果

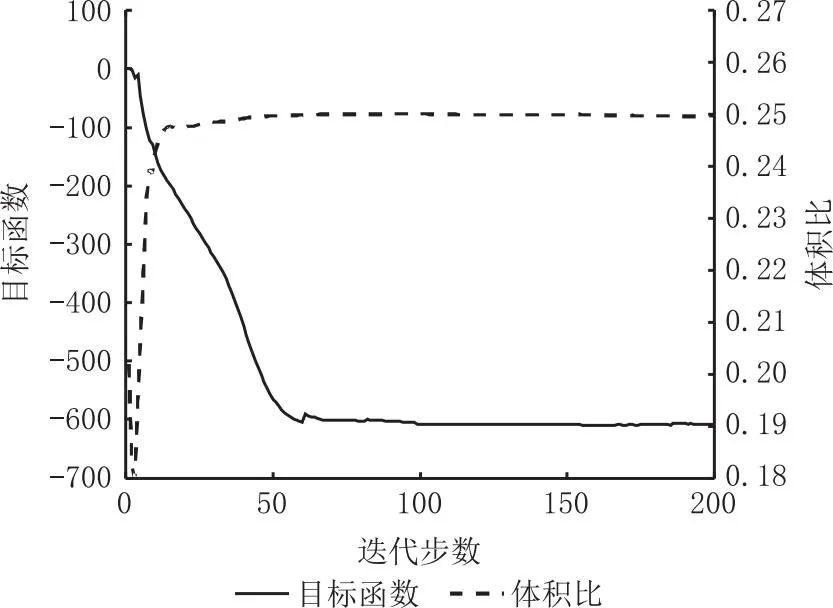
图11 考虑最小尺寸控制的夹持器拓扑优化迭代历程(dmin=4.5)

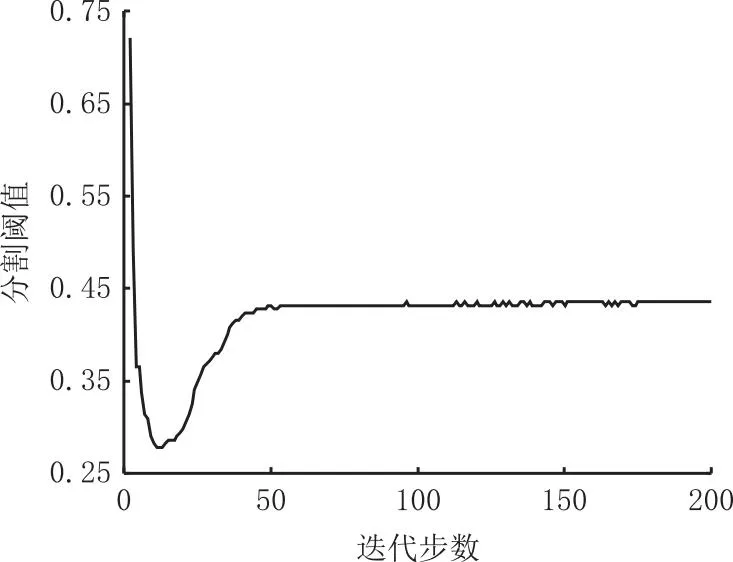
图12 分割阈值迭代过程(dmin=4.5)

(2) 不同最小控制尺寸

同样地,为分析不同最小控制尺寸对夹持器拓扑优化结果影响规律,选取最小控制尺寸dmin分别为3.0,4.0,5.0,6.0进行流体压力驱动柔性夹持器拓扑优化设计,获得夹持器拓扑构型如图13所示。随着最小控制尺寸dmin增大,考虑最小尺寸控制的拓扑优化获得的压力驱动夹持器拓扑构型发生明显变化,夹持器结构的最小特征尺寸变得更大,均满足最小尺寸控制,类铰链结构均得到有效地抑制;且目标函数f随之减小,即互应变能和应变能比值逐渐减小,如表4所示。

表4 不同最小控制尺寸的夹持器拓扑优化结果

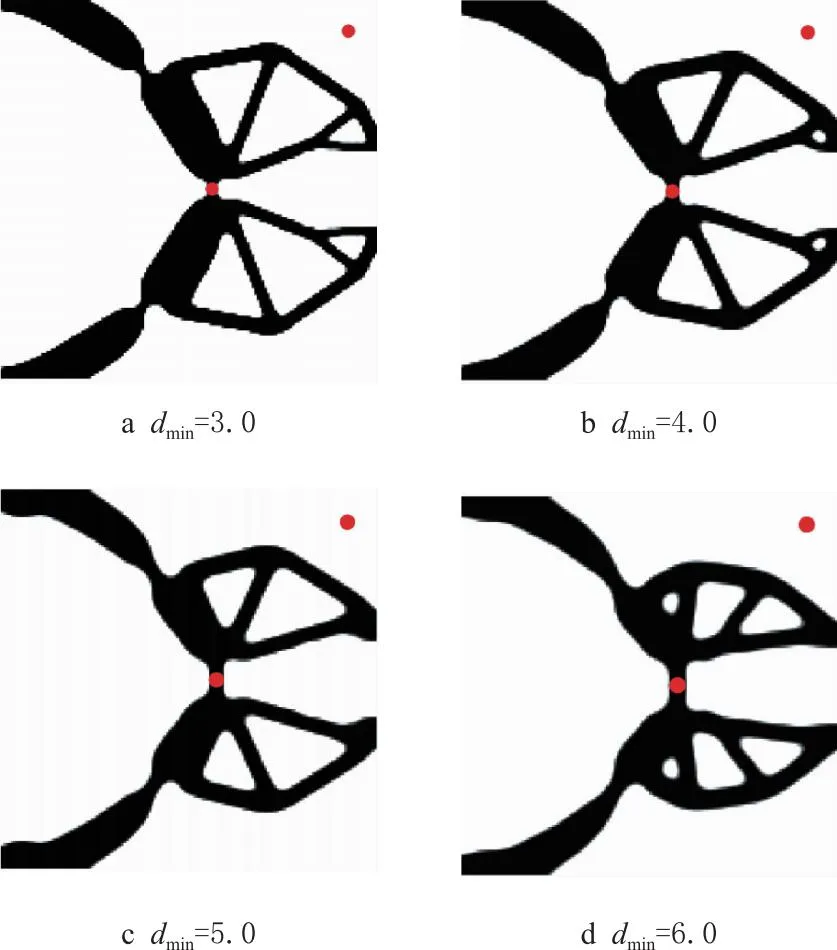
图13 不同最小控制尺寸获得的夹持器器拓扑构型(g*=0.25)

5 结束语

本文采用达西定律结合排水项计算流体压力载荷,利用Otsu算法和并行拓扑细化算法提取柔顺机构的骨架特征,从而构建最小特征尺寸控制,实现了考虑最小尺寸控制的压力驱动柔顺机构拓扑优化设计。与无最小尺寸控制的压力驱动柔顺机构拓扑优化结果比较,考虑最小尺寸控制的拓扑优化获得的压力驱动柔顺机构拓扑构型有所不同,获得的结构最小特征尺寸满足设计要求,且类铰链结构能得到有效抑制。在相同许用体积比条件下,随着最小控制尺寸增加,考虑最小尺寸控制的拓扑优化获得的压力驱动柔顺机构型最小特征尺寸变得更大,均能满足最小尺寸控制,但是互应变能与应变能比值逐渐减小。

本文所提方法有效地控制压力驱动柔顺机构构型的最小特征尺寸,获得的机构便于加工制造。本文基于线弹性理论进行研究工作,但实际应用中压力驱动柔顺机构有可能发生大变形,需要采用非线性有限元理论进行建模。因此,如何考虑几何非线性进行压力驱动柔顺机构拓扑优化设计有待进一步研究。