面向精度提升与工艺改进的容差分配多目标模型融合方法

郭飞燕,宋长杰,张 硕,童清云,白雪涛,刘连喜

(1.北京科技大学 机械工程学院, 北京 100083;2.北京星航机电装备有限公司,北京 100074)

0 引言

容差分配作为复杂机械产品制造过程中的一个重要环节,直接影响产品装配性能。装配性能指零组件按照一定的工艺方案完成装配后,形成的装配体质量指标参数,主要包括产品装配精度与装配内应力两方面。随着现代制造技术数字化、智能化程度的不断提高,在数字孪生、智能算法等技术的引入带来了更为高效的生产效率与高质量的制造性能的同时,也对产品生产提出了质量更高、成本更低、性能需求针对性更强等要求,使得传统的基于工程经验而设立的容差分配方案已难以保障产品装配性能[1-2]。在本文涉及的航空航天制造领域中,装配精度多指产品对缝间隙与外形阶差等装配协调质量,装配应力则指装配过程中与装配完成后产品内部应力的分布情况,两者均直接影响产品的服役力学状态。在以容差分配优化实现装配性能提升过程中,装配精度与装配应力的提升相互冲突、彼此竞争,同时各目标模型数据含义与数值量化计算结果(即加工成本、质量损失与修配成本具体的建模计算数值)存在较大差异,未能体现产品外形阶差装配精度提升、修配成本下降等有益效果,导致现有多目标容差分配优化存在着各目标模型难以均衡与优化偏离预期等问题。

针对传统容差分配技术存在的盲目性,为构建真实有效的容差优化模型,国内外学者针对模型的精确构建与算法的改进展开了大量研究。结合装配误差累积因素,HELING等[3]考虑容差优化模型中各尺寸链的关联关系,并以此建立关联公差的容差优化模型,为优化具有尺寸关联关系的尺寸链容差提供了可能性;杨丹等[4]在装配偏差建模环节对雅可比旋量法进行改进,将装配体双侧多点连接特征引入装配约束得到可准确描述偏差传递关系的氢氧泵多点连接偏差模型,同时在容差优化模型约束建立环节引入多点连接要求与几何精度指标要求,得到不同精度指标要求下的容差优化结果;朱永国等[5]针对交点装配构建各交点轴线的T-Maps并进行统一表示,之后采用闵可夫斯基对协调要素的公差图进行累积,并依据累积的几何关系完成公差累积与分配。考虑到具体的容差优化分配目标,CHALI等[6]提出一种基于制造难度系数与遗传算法的容差优化方法,其所提出的容差优化模型将考虑难度系数的功能需求容差作为具体约束;穆晓凯[7]通过将包含零部件制造及装配变形的小位移旋量映射到公差域的方法,分别以经济性要求作为优化目标,以零部件加工精度及装配功能要求作为约束,对航发转子各级盘的配合表面误差进行优化,体现了经济性与接触性能要求;施祥玲等[8]在建立多个目标优化模型的基础上,将装配功能要求与经济加工能力同时作为约束条件,并通过构建归一化目标函数的方法从NSGA-Ⅱ算法解得的Pareto最优解中获取期望解;CHENG等[9]将田口质量损失函数引入机械装配公差优化模型中,通过考虑公差成本与质量损失对容差优化结果进行验证,使得总装配成本降至最低;ZHANG等[10]针对传统的二次质量损失函数难以适用于分级产品容差设计的问题,在函数原有基础上进行了扩展,建立分级产品标称最佳、越大越好与越小越好的质量损失函数模型,使得质量损失模型在分级产品容差设计中具有良好的可操作性;张岩等[11]将装配成本控制作为容差优化的目标之一,融合容差加工成本与质量损失得到多目标容差优化模型,可实现不同装配方法约束下的公差优化设计。针对容差优化分配模型的求解,HALLMANN等[12]对容差优化原理所包含的基本思想、术语及数学公式进行详细的介绍,并对优化问题、容差成本模型、技术系统模型与容差分析模型的不同特征进行讨论;PENG等[13]针对并行公差分配优化展开研究,采用并行工程方法,将容差分配问题公式化,得到一个综合模型并运用非线性编程软件包进行求解,实现加工成本与质量损失的平衡;LIU等[14]在研究多目标容差分配优化的基础上,通过分析获得了能够使组合目标函数最小化的闭式解,在一定程度上降低了求解计算的复杂程度;LI等[15]提出一种基于统计公差模型的三维公差分配方法,通过允许使用不同的目标函数来实现不同的目标,可有效解决具有不同功能方案中的分配问题;荆涛等[16]针对容差分配过程中遇到的大规模非线性优化问题,提出一种蒙特卡洛-自适应差分进化(Monte Carlo-Adaptive Differential Evolution algorithm,MC-SADE)优化算法,其优化收敛性与稳定性更好,提高了容差分配的效率与稳定性。此外,考虑到生态设计在制造领域的兴起,HOFFENSON等[17]将产品生产经济可持续性与环境可持续性作为优化目标,通过得到易于拆卸的零件设计可使得零件减少63%的环境影响;AJANI等[18]考虑装配过程中形变对装配功能要求与质量损失的影响,提出一种非刚性装配的容差优化方法;GOETZ等[19]验证了早期鲁棒性设计在容差优化设计中的重要作用。上述文献主要针对与容差相关的产品性能模型构建与融合工作,并采用智能算法对容差多目标优化模型进行求解,在得到可靠的容差分配方案的同时,也存在一些不足:①现有文献中对各误差组成环节的优化,较少考虑加工环节、装配精度累积、装配后的修配补偿环节等方面的综合,且与装配工艺过程的关联性较弱,因而多采用各目标模型直接相加求和或是经验判断各模型权重的模型融合构建方法。这些方法未能考虑各个模型间数据含义与数值大小差异导致的失衡问题,采用对各个单目标模型结果直接求和进行融合的方法缺乏说服力,经验判断也难以解决模型数值失衡的问题。②通过容差优化结果可在一定程度上识别装配工艺关键环节,良好的装配工艺也可有效减轻容差优化压力,但容差优化设计与装配工艺方案的改进间的有效关联性需加强。

考虑到现代产品对装配质量的高性能要求,采用容差优化的方法难以满足生产验收标准,故常采用修配法装配,现有优化分配模型较少将修配成本减小作为一种优化目标,这样将难以规避由修配环节带来的装配经济成本增加、生产时间延长与产品服役力学性能下降等问题。针对产品修配问题,莫蓉等[20]通过修配成本、修配工时、传递比与可修配性4个指标对修配环进行量化评价,获得可装配性指标的属性值,即修配特征、修配面积、材料特征与可达精度,可有效用于装配尺寸链修配环的选择;文献[21-22]针对航空结构件提出修配方案的迭代优化方法,首先进行修配仿真与装配精度预测,确保装配精度满足要求,之后根据模糊数学隶属度理论对修配成本、难度等定性因素进行综合量化评价,实现多组修配方案的最终优化;于傲雪[23]通过考虑配合公差的产品可装性分析和形位公差的制造精度分析,设计的产品修配方案包括修配零件、修配区域、修配量等信息,并通过可视化显示有效地指导实际修配操作;陈瑞启[24]针对当前装配操作需要反复试装的问题,基于配合特征节点进行零件典型装配精度的计算分析预测,采用基于多目标函数求解的装配定位位姿协调优化,使用响应面法实现产品修配方案设计与优化,并采用模糊评价方法进行修配环的评价与决策。此外,邓向阳[25]以大型薄壁结构的加工精度、装配体几何精度指标以及偏差因子的关联关系为约束条件,以产品的加工成本、修配成本和质量损失成本为优化目标,建立薄壁结构的容差分配优化模型,并基于改进的遗传优化算法进行求解;郭俊康等[26]综合测量不确定度、装配精度、调整工时成本等因素,实现精密机床装配过程调整工艺的准确决策。通过分析,现有研究缺乏将工艺改进引入容差优化模型的研究,如改进产品定位装夹方式,调整装配误差传递网络,满足装配精度要求;或者精准设计装配完工后的修配量与修配区域,提升产品装配质量与生产效率。

综上所述,当前容差优化模型构建与求解方面均取得了一定进展,但在多目标容差优化模型融合与装配工艺改进方面仍需展开研究工作。当前容差优化的目标模型类型众多,考虑航空航天产品实际的装配生产情况,提出将修配环节优化引入至容差分配模型中。在模型融合构建中针对各目标优化模型的冲突现象也开展了相关研究,但仍难以设计决策好不同模型数据间的权重参数,即便使用博弈权重算法[27]仍难以实现结果的最优,致使模型数据出现失衡现象。因此,本文首先建立了装配误差传递累积与协调误差模型用以计算产品装配精度;之后,从装配精度提升与装配工艺改进两大方面出发,提出一种可避免数据失衡与优化偏离的多目标模型权重参数分配方法,实现容差优化分配模型的融合构建;最后,采用加速粒子群算法(Acceleration Particle Swarm Optimization, APSO)对模型进行求解,获得优化后的容差分配方案,并对某型航天器分段式机翼对接装配过程中的定位装夹方式、修配补偿操作与各组成误差环节进行改进,实现产品装配精度与对接协调质量的有效保障。

1 装配误差传递累积与协调误差模型构建

在产品的生产与装配过程中,基准零件偏差的存在会使得装配零件发生位姿变动,该位姿变动会随着后续零件的装配进行传递,同时各零件的制造误差、定位误差在装配过程中也会发生传递累积,最终位姿变动与误差累积发生相互耦合并作用于机械装配体上,从而影响机械产品的装配精度。考虑到零件配合误差引起的零件上不同关键特征间的位姿变动,本文首先分析复杂装配体配合特征间的误差耦合关系,寻找与装配协调精度相关的偏差源,构建基于误差源公差域的装配特征几何误差旋量模型,用以反映其特征变动情况;其次,根据各零组件之间关键特征的配合关系,明晰装配协调误差的传递路径及网络,并建立同一装配零件上不同特征间的实际变动关系模型,构建单个装配体的误差累积计算模型与多装配体间的协调误差模型,上述过程如图1所示。

图1 装配协调误差计算过程

1.1 装配特征几何误差源旋量模型构建

首先获取零部件生产的装配性能要求,如装配位置、间隙、阶差等协调精度要求,并将协调精度要求逐个分解为便于测量与计算的特征点位、特征面等信息。之后获取关键测点及对应的关键几何特征,并构建零部件上的关键几何特征在尺寸公差与形位公差共同约束下的误差旋量模型[28],具体地,采用运动学理论与小位移旋量法(Small Displacement Tensor, SDT),将装配零件所包含的典型直线、平面、空间曲面等几何特征的位置变动情况转化为误差旋量模型矩阵与不等式的形式,并将其映射到公差域,即实际加工制造得到的零件尺寸和理想零件间尺寸允许变动的最大范围。各类特征的误差旋量模型及约束不等式间的关系描述如表1所示。

表1 各类特征的误差旋量模型及约束不等式间的关系描述

1.2 装配协调误差传递累积模型构建

在零部件装配过程中,以某一零件作为基准进行装配时,由于基准零件存在着几何误差,下一个零件的装配位置会产生相应的变动误差,该误差与装配零件自身几何误差发生耦合并向后传递。对于零部件配合间的误差传递,其本质上是各零部件误差旋量模型中的误差分量在装配精度要求方向上的传递与累积。为便于分析偏差传递机理,考虑由配合误差引起的零件上不同关键特征间的位姿变动,并以特征误差源变动模型为基础,建立装配协调累积误差的传递流程图,如图2所示,图中实线代表零部件理论装配位置,虚线代表零部件实际装配位位置。

图2 装配协调误差累积传递示意图

根据表1中的误差旋量模型,定义零件Ⅰ和零件Ⅱ上关键特征F1i和F2i的制造误差在各自局部坐标系O1,O2中为:

ΔF1i=(α1i,β1i,γ1i,u1i,v1i,w1i)T,

ΔF2i=(α2i,β2i,γ2i,u2i,v2i,w2i)T。

根据零件坐标系与全局坐标系的转换关系,得到其齐次坐标变换矩阵;

忽略高阶项,关键特征F1i和F2i相对于全局坐标系中的误差分别为:

θz1,u1+dx1,v1+dy1,w1+dz1)T=

对于零件Ⅰ与零件Ⅱ装配的配合误差δ(1,2),其由两零件在关键特征F1i、F2i的制造误差所引起,表达式为:

(7)

设零件Ⅰ与零件Ⅱ间相互配合区域的尺寸范围为Δh=(0,0,0,Δhx1+Δhx2,Δhy1+Δhy2,Δhz1+Δhz2)T,则由两零件的配合误差δ(1,2)引起零件Ⅱ的姿态变动量为:

(8)

在零件Ⅰ与零件Ⅱ装配的累积误差的具体计算过程中,先将Δp12转换为误差矩阵形式TΔp12,采用齐次变化将功能特征配合表面的小位移旋量模型转换为误差矩阵形式,则零件Ⅰ与零件Ⅱ的配合误差矩阵为:

(9)

式中 Δu12,Δv12,Δw12表示特征F2i相对于F1i在全局坐标系中的空间位置差值。

(10)

(11)

忽略高阶微量对位姿误差的影响,将Tδ2转换为矢量形式,得到零件Ⅱ上与零件Ⅲ相配合的零件特征F2j在各方向上变动误差的累积分量形式:

Δγ12+Δγij,Δu12+Δuij,Δw12+Δwij)。

(12)

以此类推,假设当前装配体共有n个零件,将前一装配体误差引入到下一个装配体,则整个装配体的最终累积误差预测结果为:

(13)

最后,通过蒙特卡洛法获取装配误差在三维空间内的变动范围及分布规律,然后统计误差均值。其生成公式如下:

(14)

X=μ+σ·ξ。

(15)

其中:ξ为服从(0,1)内正态分布的随机数;U1、U2为(0,1)范围内服从均匀分布相互独立的随机数;μ、σ为装配误差的均值与标准差;TU、TL为装配误差变动范围的上、下界;Z为设定的标准化正态数,通常认为Z=3;X为服从N(μ,σ2)正态分布的随机数。

假设配合协调的两装配体A与B最终累积误差分别为δAn、δBn,则最终可得出两者的装配协调误差预测结果为:

∑A,B=|δAn-δBn|。

(16)

2 容差多目标分配模型融合构建

容差多目标分配模型本质上是一种能够表征产品综合装配性能与各误差组成环节间关系的数学模型,在多目标容差分配优化模型寻优过程中,由于加工成本、质量损失与修配成本模型的数据在含义上不统一,数值大小上也存在较大差异且相互作用关系复杂,如加工成本面向零件的加工环节、质量损失面向产品的装配精度、修配成本则面向装配完成后的修配补偿工作,由于三者含义与量纲均不相同,① 面向零件加工环节的加工成本模型,计算结果量纲为元;② 描述产品装配后精度数值与设计要求装配精度数值间差距的质量损失模型,计算结果无量纲;③ 面向装配完成后不得不采取修配补偿操作的修配成本模型,计算结果量纲为元,三者的计算结果在数值大小上通常不在同一数量级上,而且不同模型之间存在着优化结果上的冲突或竞争关系,同时决策变量的调整也会影响其他目标的达成情况,例如加工成本的下降会导致装配质量损失与修配成本的增加,因而各模型间的协调与融合构建目标是达到三者的相对平衡状态,使得在最终的优化目标模型融合构建过程中的权重计算参数值难以取定。为准确而高效地建立面向产品装配精度提升与工艺改进的容差分配模型,提出一种可有效避免容差优化数据失衡与优化偏离问题的多目标模型权重参数计算方法,在对各目标模型进行精准构建的同时,依靠计算所得的权重参数,保障各模型间的相对平衡并使得求解优化方向符合预期效果。

2.1 加工成本-容差模型

加工成本是指在装配体各部件零件中,加工各个形状/位置等公差需要付出的经济成本的总和,属于零件加工环节,不包含修配成本。加工成本提出主要是为了避免过高公差要求的出现所带来的经济性下降等问题。对于该模型构建,首先对生产制造过程中产生的容差-成本数据进行分析并选取合适的容差成本模型进行拟合,得到精确建立的容差-成本函数;其次,对装配尺寸链各组成环的容差-成本函数进行梳理,计算得各制造误差环节的加工成本并求和,公式为:

(17)

式中:CM(Ti)为装配容差总体加工成本;n为装配尺寸链组成环的数量;Ti为第i个尺寸组成环的公差;CMi(Ti)为由第i个组成环的公差产生的加工成本。

具体地,为建立合理的公差成本优化模型,每个公差都至少需要一个成本函数以定义整体公差成本模型。考虑到工厂实际生产需求,建立基于容差外形特征的复合公差成本模型,如表2所示[29]。根据表2,可实现对多容差的统一梳理,便于得到整体的加工成本。

表2 线性和指数复合公差成本模型

2.2 质量损失-容差模型

日本学者田口玄一[30]将产品实际性能与理想性能间的偏差值认定为质量损失。本文基于田口质量损失成本函数建立质量损失-容差函数模型,所得质量损失表达式为:

L(y)=k(y-m)2,

(18)

(19)

式中:L(y)为质量损失函数,k为质量损失系数,y为产品的质量特征值,m为产品的质量的目标值,A为零件功能失效的损失系数,x0为允许参数偏离目标值最大偏差。

对于由容差引得的装配性能质量损失模型,构建工作围绕具体的装配精度指标展开。对于由装配阶差产生的质量损失,设S(Tm)为目标阶差值,S(Ti)为由各组成环容差计算得到的实际阶差,A表示因阶差导致产品装配体功能失效的损失系数,x0为实际阶差偏离目标的允许偏差值。由式(18)与式(19)可构建容差-质量损失模型:

(20)

S(Ti)=∑A,B(Ti)。

(21)

式中:CQ(Ti)为质量损失,S(Tm)为实际阶差,Ti为各组成环容差。

2.3 修配成本-容差模型

修配成本是指在产品装配完成后的修配阶段由不同修配量与修配区域所引起的时间与经济成本。对于修配成本函数的构建,首先以容差为自变量构建修配量的期望值函数,再借由工厂生产相关生产数据得到修配成本的函数模型。在生产修配环节中,当前容差分配方案下得到的装配精度无法满足装配性能要求时,才需进行修配工作,使得产品装配精度满足验收标准。同时,影响修配成本的因素众多,主要有修配量、修配面的面积、修配经济成本与修配时间成本。若生产过程中的修配成本过高,则会带来修配成本增加、生产效率降低与一定的安全隐患。因而在进行公差设计时,需对由修配环节所产生的修配成本进行控制,最大程度减小修配环节对产品生产与制造性能造成的负面影响。具体地,修配成本可表示为:

(22)

式中:S(Ti)为容差数据计算得到的期望阶差;R(T)为实现装配性能保障所能接受的最大阶差;CR(Ti)为修配成本;CArea为可由计算获得的修配面的面积;CCost为与修配表面材料、形状特征相关的修配经济成本系数;CTime为在工厂加工效率下完成修配工作所需的时间成本系数。

2.4 容差多目标优化模型约束

对尺寸链组成环容差展开优化工作时,必须考虑生产过程中工厂所具备的机床设备加工能力,保证所得优化数值能够控制在加工能力范围之内,避免过高的制造精度要求出现,考虑工厂实际加工能力的约束表达式为:

(Ti)min≤Ti≤(Ti)max。

(23)

式中:(Ti)min为在当前加工设备能力下第i个组成环公差所能达到的最小值;(Ti)max为在当前加工设备能力下第i个组成环公差所能达到的最大值。

2.5 公差多目标模型融合

加工成本最小化,质量损失最小化与修配成本最小化等优化需求的存在,使得容差优化分配求解面临着冲突的现象。为解决上述问题,结合实际装配现场,考虑产品高精度的装配要求与修配补偿操作,将加工与装配因素综合考虑之后,设定各目标模型的初始比例,并依据提出的多目标模型融合方法计算各模型权重参数,避免优化过程中侧重某一指标的优化而忽略其他指标的“偏离”情形,实现加工成本、质量损失与修配成本三者的平衡优化,精确建立最终的容差优化模型。

(1)各模型权重参数取值

在多个目标模型间的融合方面,由于各模型数据存在较大差异且相互作用关系复杂,以零件的制造误差与装配精度要求数据为基础,引入工厂产品数学模型数据、工程人员经验数据为主要支撑,提出一种可有效避免数据失衡与优化偏离方向问题的多模型权重计算方法,使各模型达到一个相对平衡的状态,具体流程如图3所示。

图3 面向精度提升与工艺改进的容差分配多目标模型权重参数取值方法

在图3中,在上述3个容差优化模型在融合构建中,3个模型在数据含义与数值大小上均不相同,若不对各模型的权重参数进行科学取定,极易产生数据失衡与优化偏离问题,导致模型优化效果较差且与装配现场的适应性不强。采用提出的融合性能需求与经验数据的多模型权重参数取值方法可有效规避上述现象。首先,结合产品装配现场的性能需求与装配工艺分析,经由现场工艺技术人员与专家对各模型重要程度进行评估,得到αCM(Tm),βCQ(Tm),γCR(Tm)三部分的初始比例c1,c2与c3;然后,读取工厂MBD模型中包含的容差数据或是由工程技术人员给出的容差经验数据,计算得CM(Tm),CQ(Tm),CR(Tm)的具体值;最后,令α+β+γ=1,并与上述比例式结合,得到各模型权重参数α,β,γ数值的求解矩阵,获得三者在容差分配总目标函数中的具体比例:

(24)

式中,c1,c2,c3为考虑现场装配情况与装配工艺分析而设定的各部分初始比例;CM(Tm),CQ(Tm),CR(Tm)为由经验数据算得的各模型数值大小。此后可由式(24)计算出后续优化实施环节所得到的α,β,γ数值,从而精确地建立起最终的容差优化模型,获取容差优化效果CM(Ti),CQ(Ti),CR(Ti)的综合评价指标R(TI)。

在容差优化分配多目标融合模型加权系数制定的可行性论证方面,本文描述的权重参数的取定并不是简单地由工程技术人员的经验数据直接确定,而是考虑了航空航天产品装配的实际情况,在容差优化分配时,充分地将加工因素与装配工艺因素有机地融合在一起,以工程技术人员的经验数据判断与原有产品公差数据作为模型输入,合理计算各个模型的权重参数。对于航空航天高端装备,十分看重装配精度指标是否满足设计要求,而且由于装配后的修配补偿操作带来的时间、人工等修配成本十分高昂,也大大延长了型号产品的研制周期,因而在取值上更加重视由于装配精度偏差所引起的质量损失、以及修配成本,加工成本的要求相对装配成本则占据的比较较少,故设加工成本、质量损失、修配成本三部分初始比例c1,c2,c3分别为0.3,0.3,0.4,以增强与装配现场的结合性;然后根据工厂经验容差数据求得CM(Tm),CQ(Tm),CR(Tm)的具体数值,带入上述求解矩阵式(24)算得各模型权重值。对于各目标模型数据值的不平衡,优化偏离需求方向等问题,该方法可对各权重参数进行有选择地放大或缩小,使CM(Ti),CQ(Ti),CR(Ti)在数值大小上保持相对一致,实现加工成本、质量损失与修配成本三者的平衡,避免三者在数值上差距较大且弱化它们之间的冲突与竞争的关系。如在优化前,质量损失数值为3.2,而加工成本数值为43,两个数值明显不在同一数量级上,采用直接求和的方法会使优化算法的方向偏向加工成本降低而非质量损失的减少。结合原有产品公差数据作为模型输入获得各模型的权重参数,可有效实现对加工成本数值的制约与对质量损失数据的帮扶,在宏观上引导后续算法优化方向与产品优化需求保持一致,使得优化后的容差数据符合预期的优化效果。同时,相比于工程技术人员直接给出权重参数,本文所提方法结合历史容差数据,一定程度上避免了由经验直接给出权重参数方法所产生的盲目性,使得权重参数计算结果更有说服力。

(2)容差分配多目标优化模型构建

基于上述多模型权重的取值计算方法,以加工成本、质量损失、修配成本作为优化目标,构建容差分配多目标优化模型,其主要包含单目标模型、综合评价指标R(Ti)、约束条件与权重参数设置,具体如下:

(25)

式中:CM(Ti)为生产加工成本;CQ(Ti)为质量损失成本;CR(Ti)为修配成本;Ti为组成环公差;α、β、γ分别是加工成本、质量损失与修配成本的权重参数;S(Ti)为实际阶差,S(Tm)为理想阶差,(Ti)min为第i个组成环在当前加工能力下所能达到的最小公差;(Ti)max为第i个组成环在当前加工能力下所能达到的最大公差;R(Ti)为装配体综合性能评判指标,优化算法以实现R(Ti)最小化为目标,所得的R(Ti)越小,代表产品综合性能就越好。

3 基于加速粒子群算法的模型优化方法

3.1 加速粒子群优化(APSO)算法原理

粒子群优化(Particle Swarm Optimication,PSO)作为一种基于种群的随机优化算法[31],其对群体行为进行模拟,基于全局最佳位置gbest与个体最佳位置pbest对粒子位置进行更新,个体代表式(26)着在d维空间中的潜在解,粒子群中的粒子在寻优空间的移动可表示为:

(26)

(27)

当前标准粒子群优化技术已被广泛用于各种研究工作中,而粒子群算法内部系数选取仍缺乏有效推导,易产生早熟现象与多样性损失等问题。为了解决这一问题,相关领域人员提出了多种PSO算法的改进版本。加速粒子群优化算法(Acceleration PSO,APSO)作为标准PSO算法的一种变体[34],其加速度系数基于适应度值选择,可有效解决标准粒子群优化算法早熟收敛的问题。APSO算法中加速度系数值的计算如下:

nc1=c1×(1-λ),

(28)

nc2=c2×(1-λ),

(29)

(30)

(31)

其中:χ为变异概率;ω、φ为系数因素;fmax、fmin、favg分别为粒子的最大、最小及平均适应度。通过上述计算可获得加速度系数nc1及nc2,进一步得到粒子速度计算公式:

(32)

式中:a1与a2通过比较具有最小适应度值的粒子与pbest粒子值而计算得到。若两粒子值相同,则a1与a2的值均为0,否则值均为1。

3.2 多目标容差优化模型输入与求解

为提升模型输入及程序编写效率,将优化算法程序分为目标模型模块、约束施加模块、算法实现模块与子函数模块4个部分。对于目标函数文件编写,基于上述容差分配多目标优化模型,在MATLAB软件中编写加工成本、质量损失与修配成本的函数模型,并根据计算得的权重参数对各模型数值加权求和得到最终的目标函数;对于约束施加文件编写,主要依赖于不等式的设立为后续优化建立约束空间;算法实现模块部分主要通过读取目标函数文件与约束文件,设置变量上下限、粒子种群大小、迭代次数等算法参数,并调用APSO算法代码,实现对目标函数的优化求解;对于子函数模块,算法实现模块的运行需要调用各项子函数文件,包含APSO求解、粒子函数初始化、罚函数设立等文件。完成优化目标函数的输入与APSO算法程序的构建工作后,运行算法实现模块,即可获得优化后的各组成环容差数值。

4 实例验证

4.1 分段式机翼结构介绍与装配工艺方案分析

对于某航天器分段机翼结构,机翼各段组件之间在连接带板处采用多孔配合的方式进行螺栓连接,在满足机翼各组件段外形装配精度的同时,还需保证以阶差、间隙等形式表现的多个高要求装配协调精度指标,机翼装配结构与加工技术要求分别如图4与表3所示。在产品生产制造过程中,还存在着装配工艺方案制定缺乏量化指导分析、机翼外形装配误差累积传递结果难以预测、由过大的修配工作量引起的装配效率低、装配容差分配方案难以满足性能需求等问题。为在产品设计与制造环节实施精细化的尺寸管理,并为机翼装配性能的提升提供理论计算指导依据,需对分段式机翼对接结构涉及的关键误差组成环节进行优化,使得装配结果达到预期的高性能技术指标。

表3 各段机翼加工技术要求信息数据表 mm

图4 机翼Ⅱ(左)与机翼Ⅰ(右)结构与装配特征示意图

4.2 分段式机翼装配体协调误差传递累积与工艺方案优化

结合分段式机翼装配工艺过程和装配指标要求,将机翼底部与机身的配合接口认定为关键装配位置,两端机翼的结构与关键装配特征如图4所示。以该位置为装配定位基准,其误差变动会显著影响机翼外形装配效果,其中E0表示各段机翼底部接头的制造误差,E1表示各段机翼与装配工装间的配合误差,E2表示两段机翼的对接误差。在各段机翼装配外形误差的建模中,基于SDT模型完成装配特征几何误差旋量模型构建。具体地,首先在机翼翼面上建立坐标系:原点O位于机翼底部接口上长圆孔中心处;X向为航向,Y向为翼展方向,Z向为高度方向。根据表3中的数据,机翼底部接口处长圆孔公差域的旋量模型及约束不等式为:

(33)

机翼底部发生的位置变动会沿机翼展开方向成比例地增大,最终在距离机翼底部最远端的位置形成位置误差,两段机翼外形阶差处的结构如图5所示。此外,考虑机翼外形表面的法线方向,建立机翼装配阶差尺寸链如图6所示。其中,L0为封闭环,其余为组成环,取L6为修配环。结合翼面外形在公差域内变动(图5),其误差旋量模型及约束不等式为:

(34)

图5 翼面在法向方向上的误差变动及对接结构形式

图6 某型航天器机翼装配阶差尺寸图

首先计算机翼底部与工装夹具装配产生的装配误差。根据机翼接口上的长圆孔圆心的旋量模型和约束不等式(32)计算推算出孔轴的垂直度,从而计算出机翼离机翼底部的最远段的位置变动,通过关键装配尺寸链的求解,得到机翼Ⅱ坐标YOZ平面上的位姿变动为1.65 mm,孔轴的垂直度β=±0.1°,两段机翼在相互对接处的装配阶差XN1=2.54 mm。此后,根据机翼各组件间顺向阶差小于1 mm的装配要求,采用蒙特卡罗模拟法计算其满足机翼装配指标要求的概率,得到两段机翼间的装配阶差满足1 mm要求的概率为16%。由于机翼外形型面精度要求为±0.8 mm,以机翼底部最远的两个工装接口处的交点长圆孔中心为基准进行定位装配产生的位置变动大于机翼装配外形型面精度,对后续的机翼与机翼之间的对接误差会产生较大影响。根据机翼外形装配指标要求,要使机翼外形型面精度限定在±0.8 mm范围内,根据装配基准的变动几何关系分析,机翼底部在接口处上的交点长圆孔产生装配位置变动需小于0.0242 mm。仅使用机翼底部的接头定位工装将很难实现预期的装配目标,因此,在装配定位过程中,在工艺方案层调整为使用定位精度为0.2 mm的外形卡板装配工装以保障机翼外形的装配质量,如图7所示。

图7 采用外形卡板的机翼外形装配方案

增加卡板后,对各段机翼的对接阶差进行分析:由于改变了机翼产品的定位方式,引起装配阶差的误差源的发生了变化。对装配定位后各段机翼之间对接处的阶差进行计算,可知两段机翼相互对接处之间的装配阶差的误差累积XN1=1.05 mm,满足装配精度要求。同时在计算过程中发现,各段机翼骨架的3D打印成形误差占据了大部分的阶差数值,需对现有3D打印精度±1 mm进行适当地提升。此外,如果将工装定位卡板的定位精度限定在0.1 mm,计算得到的最终阶差数据会有所提升,但是由于机翼骨架的3D打印成形误差对工装定位误差较大,阶差精度提升效果仍然有限。

4.3 机翼与外形阶差尺寸组成环节优化模型构建与求解

对于机翼外形阶差的各尺寸组成环节(图6),在模型求解过程中,为使得综合评价指标最小化,优化算法会偏向降低数值最大的加工成本模型而非质量损失与修配成本的降低,所得到的优化结果仅是大幅度降低了加工成本,对于质量损失与修配成本的降低效果不明显。为充分缓解目标间的冲突问题并使加工成本、质量损失与修配成本三者达到一种较为平衡的状态,避免由模型数据失衡与优化偏离带来负面影响,以下从容差多目标优化模型融合构建与容差多目标模型优化求解两方面展开验证工作。

(1)容差多目标优化模型融合构建

依于上述模型建立方法,结合工厂生产数据分别构建加工成本、质量损失与修配成本模型。对于加工成本模型构建,函数类型选取线性和指数符合公差成本模型,并依靠工厂数据库进行拟合;对于质量损失模型构建,认为质量损失由装配实际外形阶差值与理想外形阶差值间的偏差引起;对于修配成本模型构建,认为修配成本与最大修配量及修配面积成正比,系数取值与修配材料、修配经济成本等相关。各模型表达式及参数设置如表4所示。

基于面向精度提升与工艺改进的容差分配多目标权重参数计算方法,计算各权重参数,并对各模型加权求和,得到多目标容差优化模型。具体地,首先获取工厂MBD模型包含的容差数据或由工程人员生产经验所设立的容差数据,并以此计算在该容差分配方案下的加工成本、质量损失、修配成本数值。之后,设定三者在综合评价指标R(Tm)中的初始比例c1,c2,c3分别为0.3,0.3,0.4。此时零件制造误差数据Tm已知,也即CM(Tm),CQ(Tm),CR(Tm)均为已知量,设α,β,γ为未知数,由参数求解矩阵:

(34)

即可求得α,β,γ的具体值,得到装配性能综合评价指标R(Tm),完成多目标优化模型的融合构建。

(2)容差多目标模型优化求解

优化求解方面,选择MATLAB软件作为上述数学模型的构建与算法的实现平台。依赖于上述模型建立,在程序中编写目标函数文件、约束函数文件、APSO算法文件及各子函数文件。首先基于上述数学模型对目标函数文件与约束函数文件进行编写,之后在APSO算法文件中对目标函数、约束函数文件及各子函数文件进行调用,并设置算法的各项参数,具体如表5所示。

为验证装配工艺改进的有效性,分别对装配工艺改进前后的装配误差传递进行建模,并对两种装配工艺方案下涉及到的容差结果进行优化对比。分别对4.2节中的两种装配工艺方案的容差进行优化分配,两种工艺方案下的容差优化结果如表6与表7所示。

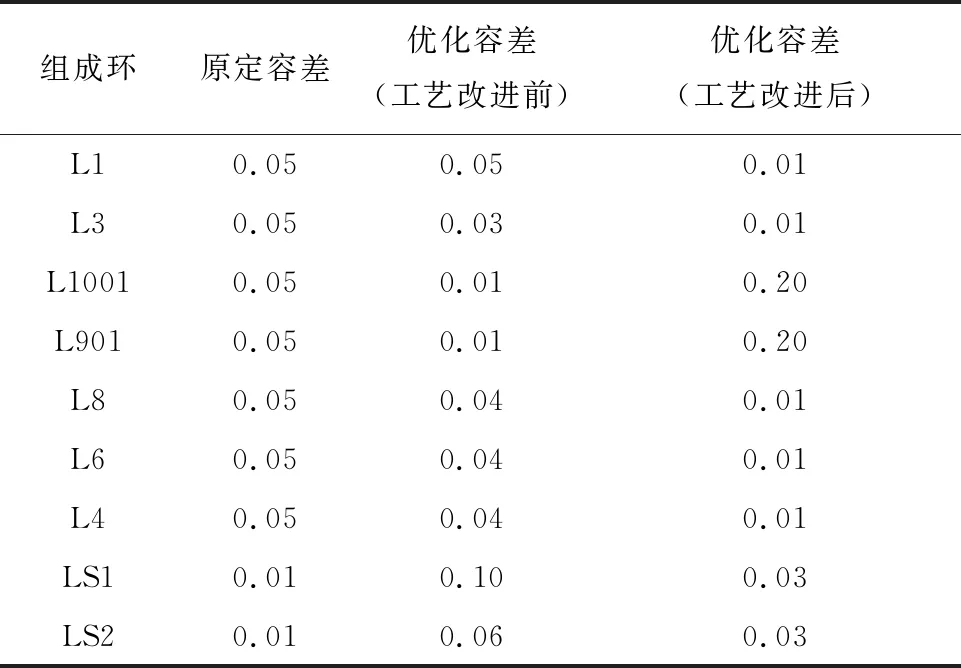
表6 两种工艺方案下的容差优化结果

表7 两种工艺方案下的容差优化效果

对于改进前的装配工艺方案(即机翼底部接头作为装配基准),由经验数据求得的容差加工成本CM(Tm)、、质量损失CQ(Tm)与修配成本CR(Tm)分别为40.60、40.82与38.46,各目标模型的数据含义不统一,同时考虑到产品生产遇到的主要矛盾是装配精度难以保证与修配操作的工作量过大,特别是由修配作业产生的人力成本与时间成本明显高于产品容差的加工成本,故而将优化重心放在了修配成本与质量损失的降低上。综合考虑上述装配现场情况,各模型初始比例的取值上对加工成本的要求较少,更加重视由于装配精度偏差所引起的质量损失、以及修配成本,因而将各模型初始比例设置为0.3∶0.3∶0.4。计算得到各模型权重分别为0.2566、0.2553与0.4881。对于改进后的装配工艺(即采用外形卡板的定位方式),由经验数据求得的容差加工成本CM(Tm)、质量损失CQ(Tm)与修配成本CR(Tm)分别为36.28、2.17与4.70,可发现:加工成本与后两者的数值大小明显不在同一数量级上,如果不对权重参数进行调整,由于加工成本数值过大,采用直接相加的形式会导致优化求解大幅度偏向加工成本的降低,而弱化了对质量损失与修配成本的降低效果,从而产生数据失衡与优化结果偏离预期、而且与实际装配需求不符等问题。故设初始比例为0.3∶0.3∶0.4,使得优化重点偏向质量损失与修配成本降低,经式(24)计算得各模型权重分别为0.0441、0.5881与0.3678。

所取得的优化效果如图8和图9所示。通过对两种装配工艺方案进行分析,可知:采用加卡板的装配工艺中的各模型优化幅度明显小于未加卡板的装配工艺优化幅度,充分表明装配阶差主要由底部接口基准引起。通过在装配过程中增加卡板,可有效避免各段机翼底部接口基准误差对阶差产生的影响。装配工艺改进前,机翼对接外形阶差与修配成本分别降低94.68%与83.49%,而装配工艺改进后上述两项装配指标分别降低11.21%与8.50%,表明通过产品定位装夹方式的改进,产品的质量损失与修配补偿操作工作量均有所下降,一定程度上提高了产品外形阶差装配精度,使得两者的优化幅度有所降低。同时,采用本文提出的多目标权重参数计算方法,所得到的质量损失与修配成本的提升幅度显著大于加工成本,与预期优化目标相符,表明由容差优化驱动的修配成本降低与装配工艺改进具有较强的可行性,可有效避免各目标模型数据失衡与优化偏离需求方向等问题。

图8 初始装配工艺方案下优化前后各模型指标对比

图9 改进后的装配工艺方案下优化前后各模型指标对比

5 结束语

通过分析复杂装配体配合特征间的误差耦合关系与各零组件之间关键特征的配合关系,明晰装配协调误差的传递路径及网络,本文建立了同一装配零件上不同特征间的实际变动关系模型,获得了单个装配体的误差累积与多装配体间的协调误差数值。

综合加工与装配工艺因素,分别建立加工成本、质量损失、修配成本3个单目标优化模型,并提出可避免容差优化失衡与优化方向偏离的多目标模型权重参数分配方法,同时采用加速粒子群算法求解多目标容差优化模型,得到了可有效提升装配误差与降低修配成本的容差分配方案。

以某型航天器机翼部件对接装配优化为例,引入外形卡板定位改进了产品的装配方案,使用卡板定位方案前后机翼对接外形阶差与修配成本分别降低了94.68%、83.49%与11.21%与8.50%,有效地保障了产品装配精度与对接协调质量。

在下一步的研究工作中,需结合生产现场的测量数据,进行面向真实数据的装配容差优化分析及最终的装配测量验证,切实指导装配实际生产。