基于HHT-LSTM的冬奥会临时设施运行趋势预测方法研究

常明煜，田乐，郭茂祖

（1.北京建筑大学 电气与信息工程学院, 北京 100044; 2.北京建筑大学 建筑大数据智能处理方法研究北京市重点实验室, 北京 100044）

临时设施故障预测是学界研究重点之一，通过提前预判相关设施的状态和未来一段时间的变化趋势，有助于提高其安全性。在大型体育赛事中，因临时设施具有安装方便、拆卸容易、能重复使用的特点，因此会有大量修建的临时设施，其中就包括临时看台、转播塔、临时桥架以及为偏远赛场电力运营所建造的输电塔等临时设施结构。由此可见，临时设施在我国建设体育强国中有着愈发重要的地位。

本文研究主要是基于2022年举办的北京冬奥会。为举办绿色奥运，勤俭办奥，大量易于搭建和重复利用的临时设施被大范围采用，其中就有临时看台以及放置转播设备的转播塔等。临时看台主要承受人群荷载，当人群拥挤、摇摆、跳跃时，容易引发强烈振动，直接影响看台结构的整体强度和刚度，导致该类结构安全事故可能发生，而转播塔也可能由于施工缺陷、各种复杂荷载的作用或者杆件老化等原因，转播塔结构在运行中会存在疲劳裂纹、螺栓松动等损伤。除此之外，转播塔结构比较高耸，而且其最上面的平台会放置转播设备，使得转播塔对风荷载、雪荷载、低温环境等具有很强的敏感性。因此，有必要对看台、转播塔等临时设施结构进行荷载和损伤识别，从而能够为建立冬奥临时设施结构安全智能预警提供关键技术支撑。

本文提出了以希尔伯特黄变换（Hilbert-Huang transform, HHT）和长短期记忆网络（long shortterm memory network, LSTM）为基础的一种全新的组合模型。希尔伯特黄变换由经验模态分解（empirical mode decomposition, EMD）和希尔伯特变换（Hilbert）两部分组成，通过EMD将给定信号分解成若干固有模态函数（intrinsic mode function,IMF)，这些函数是满足特定条件的分量；然后再对各个分量进行Hilbert变换得到瞬时频率。相比于传统的时频分析方法，瞬时频率和幅度都可以通过HHT得到，而且该方法所得时频矩阵更精细，同时也不存在频谱泄漏风险。

HHT具有自适应性和清晰的物理含义，是一种适合处理突变信号的方法，可以有效解决线性和平稳性束缚问题，可以有效提取到信号的时间、频率、能量分布特征。

LSTM网络也可以有效避免长期依赖性问题。所谓长期依赖的问题指的是随着时空距离的增加，信号之间的相关性常常变得越来越弱，不确定性越来越大。传统的神经网络没有记忆功能，而循环神经网络（recurrent neural network,RNN）能够连续不断地进行信息循环，保证信息存在，RNN可以利用以前的信息对当前任务进行相应的操作，如果这次任务的有用信息与需要进行处理信息的地方之间距离较远，容易导致RNN不能学习到有用的信息，导致推导任务失败，造成梯度消失或梯度爆炸。LSTM可以避免RNN梯度消失解决长依赖问题，因此本文采用LSTM来解决临时设施未来趋势预测问题。该算法为临时设施运行趋势预测提供了一种有效的方法，实现临时设施倾斜、振动等状态信息的监测与智能分析需求，及时捕捉到异常点，最大限度降低安全隐患。

1 临时设施预测方法相关工作

对于临时设施趋势预测主流方法包括时间序列预测、智能算法和组合模型等。其中，传统的时间序列预测方法虽然对线性数据处理效果良好，但是处理非线性数据时该类算法的效果不佳。智能算法目前主要有机器学习和深度学习2类，其中常见的主要包括随机森林算法[1]、BP神经网络[2]、时频分析[3]与特征融合方法、小波变换[4]、傅里叶变换[5]等。文献[6]利用粒子群算法（particle swarm optimization，PSO）优化的BP神经网络来对办公建筑视觉舒适度进行预测，提供了一种高效准确的办公建筑预测方法。在日常工作中，机械设备会产生特征性的振动、噪声等信息，因此出现了很多以数据驱动和信号处理为基础的方法。文献[7]通过峭度解卷积降噪与经验小波变换的方法，达到了诊断滚动轴承故障的目的。文献[8]采取了时频变换和特征融合策略，达到了诊断内燃机故障的目的。文献[9]深入研究了以自适应经验傅里叶分解为基础的故障识别策略。文献[10]以小波变换为基础，实现了诊断液压缸泄漏故障的目的。利用智能算法虽然能很好地处理非线性问题，但在处理大样本数据时计算速度慢、计算效率低。就原理而言，组合模型通过对各个单一模型的组合，可以充分发挥各自优点，在提高效率的同时提高预测精度。此外，通过组合模型所得到的结果，比单一模型更加稳定可靠，这也是它能够广泛运用于经济、工业等诸多领域的原因所在。文献[11]通过人工神经网络和卡尔曼滤波达到了诊断浮式风力机桨距系统故障的目的。文献[12]充分结合了多点最优最小熵解卷积和增强倒频谱技术，并将其运用到诊断风电机组齿轮箱多故障中。很多预测方法不仅应用于机电设备故障预测和办公建筑领域，而且在电力负荷预测和价格数据预测领域应用也十分广泛。文献[13]利用PSO优化长短期记忆神经网络（LSTM）模型的参数，大大提高了预测精度。文献[14]结合LSTM模型处理长时间序列的优势和支持向量机回归（support vector machine regression, SVR）模型处理非线性问题的优点，并利用果蝇优化算法优化参数建立组合模型，预测了烟用白卡纸价格和短期卷烟销量，并取得显著成果。

除了设计各种模型，一些学者还结合了时频分析丰富信号原始信息，最终达到增强预测准确性的目的。如Giulia等[15]提出了经验模态分解与人工神经网络(empirical mode decomposition-artificial neural network, EMD-ANN)分解-集成模型，大幅提高了预测准确性；Tayyab 等[16]则构建了离散小波变换-神经网络(discrete wavelet transformback propagation, DWT-BP)和离散小波变换-径向基神经网络(discrete wavelet transform-radial basis function network, DWT-RBF)组合模型，预测效果也明显提升；刘艳等[17]提出的传统时序建模方法(auto regressive integrated moving average, ARIMA)组合模型也拥有不错的预测效果；赵力学等[18]通过变分模态分解-反向传播神经网络(variational mode decomposition- back propagation, VMD-BP)模型完成了水位流量的非线性拟合，所得效果也很好；詹可等[19]针对海洋环境中非线性、非平稳的实际波高时间序列，提出了一种经验模态分解与长短期记忆网络(empirical mode decompositionlong short-term memory, EMD+LSTM)短期预报模型，相比于传统的时间序列预测模型具有更高的精度；姚洪刚等[20]针对金融序列高噪声以及非线性的特点，提出了一种EMD+LSTM的金融时间序列预测模型，取得了很好的预测效果。

在设计引入时频分析的模型时，可能会存在以下不足[21]：

1)传统的时频分析方法在积分变换的过程中会产生频谱泄漏，局部细节无法被很好地刻画出来。

2)对一维信号进行转化时，虽然可以得到丰富的特征，但是特征空间的维度也会增加，这样就需要采用复杂的神经网络去进行特征提取和处理，会导致梯度消失，不收敛等问题。

因此本文采用了HHT和LSTM构建了一种预测模型。通过HHT将一维信号转换成二维的时频矩阵。HHT与传统的基于积分变换时频分析方法相比，能获得瞬时频率和幅度，时频矩阵更好地展示信号在不同时间和频率上的特征而且不会发生频谱泄漏。所以，HHT可以弥补传统时频分析方法的缺陷，更好地刻画信号的局部细节。

2 HHT+LSTM的临时设施运行趋势预测

2.1 HHT+LSTM组合模型

本文实验所使用的数据源于北京冬奥会延庆赛区高山滑雪中心临时看台支撑架上的加速度传感器，所测得的数据信号有不同的振幅、形态和频率存在。此数据的信号属于一类非线性非稳态的信号时间序列。如果采用传统的时频分析方法，无法有效地提本文到此类非平稳信号的特征。HHT结合了EMD和希尔伯特变换，可以计算瞬时频率和幅度，对于此类信号处理属于最佳的选择。因此，HHT的作用是将时域的信号进行转换进而得到包含时域和频域对应关系的时频图。首先采用EMD将振动信号进行分解，得到若干个内涵模态分量（IMF），然后通过希尔伯特变换计算出每个IMF的瞬时频率和幅值。最后采用LSTM来处理精细的时频特征信息完成最终的预测。

HHT+LSTM的预测模型整体框架如图1所示。在HHT+LSTM的预测模型中，可以通过EMD把原始信号分解为诸多子序列，将分解后的IMF进行希尔伯特变换，该方法所得时频分布的信号能量更加完整、精确，同时，还可以继续得到信号的Hilbert边际谱，从而达到精确反映信号幅值随频率变化规律的目的。通过信号处理方法得到的时频特征，将其作为输入送到LSTM网络进行训练和预测。下面将展开介绍希尔伯特黄变换和长短期记忆网络。

图1 HHT+LSTM的预测模型整体框架Fig.1 Overall framework of HHT+LSTM prediction model

2.2 希尔伯特黄变换

对于希尔伯特黄变换[22]而言，经验模态分解和希尔伯特变换是其最重要的部分，这个信号处理方法利用了信号的局部信息，从而获得信号某一时刻的瞬时状态。信号处理的本质都是将接收的高频实信号，结合已知的载频信息，还原出基带的复信号。在自然界中实际观测到的都是实信号，复信号是观测不到的。而在对信号处理方面，复信号相比于实信号处理起来非常容易。所以在趋势预测的任务上，本文首先采用对采集到的信号数据进行处理，将其与深度神经网络进行结合来实现更加准确的预测。

2.2.1 经验模态分解

将原始信号x(t)通过EMD分解，得到若干个IMF分量，所有IMF分量都需满足下述条件：1)极值点与零点数量之差应小于等于1；2)局部最大值与最小值的包络线间均值必须是0。具体EMD计算过程如下：

1）用一条连续的光滑曲线将时间序列信号x(t)中全部极大值点进行串联，形成上包络线xmax(t)，同上所述确定下包络线xmin(t)。定义2条包络线的平均线m1(t)：

利用原始序列x(t)与m1(t)之差得到第1个分量h1(t)：

2）对于不同的信号，h1(t)可能是一个IMF分量，一般来说它并不满足IMF所需要的条件，此时将h1(t)当作原信号，重复上述步骤，则有：

3）判断是否满足IMF分量的条件，如果不满足返回到极值计算，重新对信号进行极值和包络运算；如果满足条件，则得到IMF分量和差值。

4）判断一个差值信号是否为IMF分量，需要有一个筛选过程终止的原则，通过利用2个连续的处理结果之间的标准差SD作为判断依据：

5）当h1k(t)满足SD的值要求时，称h1k(t)为第1阶IMF，记为c1(t)：

6）从原信号x(t)中减去c1(t)得到剩余信号，即残差r1(t)：

然后将r1(t)看作一组新的“原信号”，重复上述经验模态过程，通过多次运算得到全部的IMF和残差ri(t)：

式中：i=1, 2, ···,n，当ri(t)满足判断条件之一时，经验模态分解过程终止，则原始的时间序列为

2.2.2 希尔伯特变换

EMD分解后，对每一个IMF(ci(t))分量进行希尔伯特变换，从而得到瞬时频率和幅度[23]。

式中：P为柯西主值，t和τ为时间。

从式(9)中再得到相应IMF瞬时频率和幅值：

式中：ωi(t) 和ai(t)分别为第i个IMF的瞬时频率和幅度。通过对所得全部数据的归纳，就能够得到所需的二维时频图。

2.3 希尔伯特黄变换

本文利用LSTM[24]来处理得到的二维时频图。LSTM可以避免长期依赖问题，能很好地解决时间间隔较长和延迟时间等问题，图2为具体结构。在操作过程中，首先把不同序列输入到LSTM，然后就可以利用门控单元读取、调整隐含状态向量和记忆状态向量，最终达到对各序列进行预测的目的。LSTM是一种特殊网络结构，依靠3个“门”结构可以令信息选择性对循环神经网络中每个时刻的状态产生影响。相关计算如下：遗忘门是将上一层信息与输入数据信息的加权之和，激活函数是Sigmoid，输出0～1的值，直接控制了信息传递的比例。

图2 LSTM神经元结构示意Fig.2 Schematic structure of LSTM neurons

输入门也有一个激活函数Sigmoid，决定了哪些信息会被传递：

tanh激活层用于创建隐藏层的候选值：

最后记忆层：获取隐藏层，是基于上一个隐藏层与现隐藏层的候选值，这2个值通过与遗忘门和输入门相乘，决定通过多少信息：

输出门也有一个激活函数Sigmoid，决定输出哪些信息：

最后隐藏层：先经过一个激活函数，让值控制在[-1，1]，防止梯度爆炸，然后再与输出层相乘决定输出哪部分信息，即最后仅仅输出我们确定输出的那部分：

式中：σ为Sigmoid函数，Ft为t时刻遗忘门，xt为t时刻的输入，W为权重矩阵，It为t时刻输入门，Ht-1为t-1时刻隐含层状态，C˜t-1为记忆更新向量，b为偏置向量，tanh为双曲余弦函数，Ct为t时刻的记忆单元状态变量，Ot为t时刻的输出门，Ht为t时刻隐含层状态。

3 实验结果与分析

3.1 数据来源

本实验所使用的数据源于北京冬奥会延庆赛区高山滑雪中心临时看台支撑架上的加速度传感器，在比赛现场，该传感器的主要作用是检测观众对看台的施力状态，所得数据是真实多元时间序列数据集，从占比来看，训练集占比最大，为60%，测试集、验证集则均为20%。

本数据集涵盖了4个不同位置加速度传感器在X轴、Y轴、Z轴方向的三维传感器数据。采用的数据集长度为53 217，传感器采样频率为500 Hz。相关设备每间隔10 min 采集10 s数据，并将所得数据上传到云端。

3.2 评价指标

为合理评价模型性能，本文采用均方根误差（root mean square error, RMSE)、平均绝对误差（mean absolute error, MAE）和平均绝对百分比误差（mean absolute percentage error, MAPE）3个评价指标。其中RMSE描述的是预测值和真实值之差的平方的均值开方，代表了预测的离散程度，能够很好地反映出实验数据具有更好的精度，使误差的结果和数据是一个单位级别，可以更好地描述数据。MAE描述的是预测值和真实值之差的绝对值求平均，其值越小越好。MAPE用预测值与实际值之间的差去与实际值相比，看其中占比有多大，对预测的准确度表示更加直观。上述性能指标定义为

式中：n为测试样本，PMi为i时刻的实际数据，PPi为i时刻网络的输出数据预测值。

3.3 实验设置

本文实验数据集的划分为训练集、测试集和验集比例为3∶1∶1。训练模型使用的是Adam优化器，基本参数设置分别为学习率为0.000 8，一阶矩估计的指数衰减率参数为0.9，二阶矩估计的指数衰减率参数为0.999，权重衰减参数为1×105，训练轮次为60，批处理训练参数为512，将训练集输入到模型中进行训练。本实验均在Ubuntu系统上进行，GPU为Tesla V100，内存为128 GB。编程语言使用的是Python3.6，神经网络的构建框架为Pytorch；数据的读取和计算使用的是numpy和pandas库；希尔伯特黄变换使用的是pyhht库。

3.4 结果与分析

本文实验数据采用的是冬奥会现场测得的私有数据集，本文选择24个历史数据来预测下一个时刻点的3个维度上的值。

通过HHT算法处理相关数据，再对所得数据进行经验模态分解，可以获得一个残余分量r和12个固有模态函数IMF1～IMF12，IMF0定义为原始信号。分量IMF1不规则主要是因为数据序列存在非线性和非平稳性的情况。分解所得IMF1频率和振幅都最大，且原始序列主要信息也被包含在其中，分量IMF2～IMF12的频率和振幅都逐渐下降，只能展现原始序列局部特征，结果如图3所示。

图3 经验模态分解Fig.3 Empirical mode decomposition

然后用HHT算法对每一个IMF分量进行希尔伯特变换，得到各分量的时频图，每个IMF分量均与相应频谱图对应，具体见图4。表1～3列出了各分量平均瞬时频率。从表1～3中可得，EMD分解所得IMF分量的频率表现出逐步下降趋势，而且进一步观察还可以发现各分量平均频率近似2倍关系依次降低。这样就可以将原信号分解出高频、中频和低频3种不同的信号。这也充分展示了希尔伯特的一个重要作用-频分复用。简单来说就是各个原信号在时域上共用，但在频域上相互独立的一个方式。这个方法能将各个原信号调制至不同的频率段，使得它们互不干扰，并且通过之前类似的方法总能将调制信号中的各个原信号解调出来。EMD分解出来的信号处于高频、中频和低频3种不同频率，希尔伯特变换也能很好地处理不同频率段的信号并且不会互相影响，避免了对后续预测的结果精度产生影响和偏差。

表1 高频分量频率Table 1 High frequency component frequency

表2 中频分量频率Table 2 Intermediate frequency component frequency

表3 低频分量频率Table 3 Low frequency component frequency

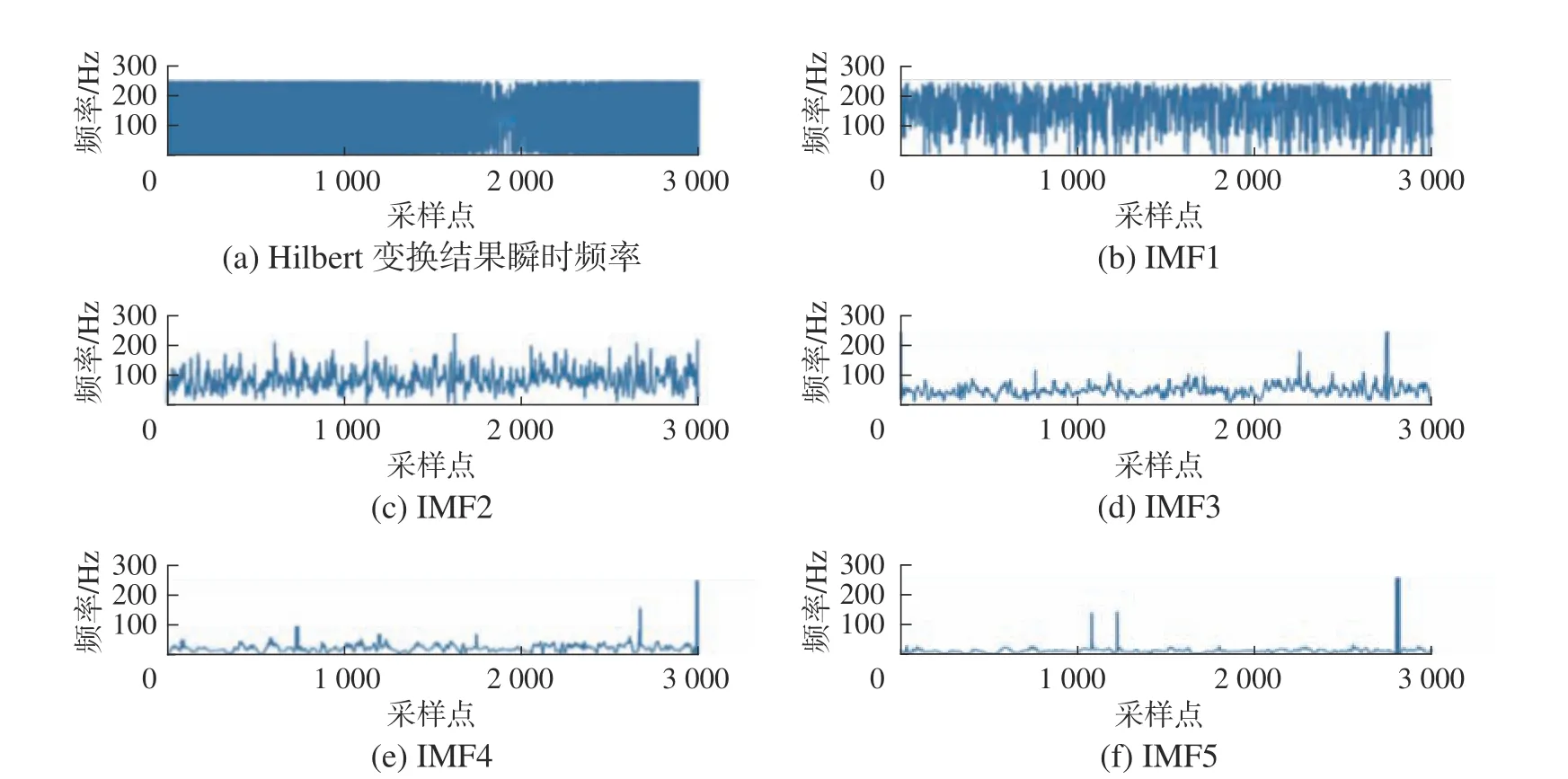
图4 各IMF分量平均频率Fig.4 Average frequency of each IMF component

在得到高频、中频和低频3种分量后，将其输入到LSTM网络中进行预测，得到了X、Y、Z轴3个维度的预测值，该组合模型预测结果如图5所示。

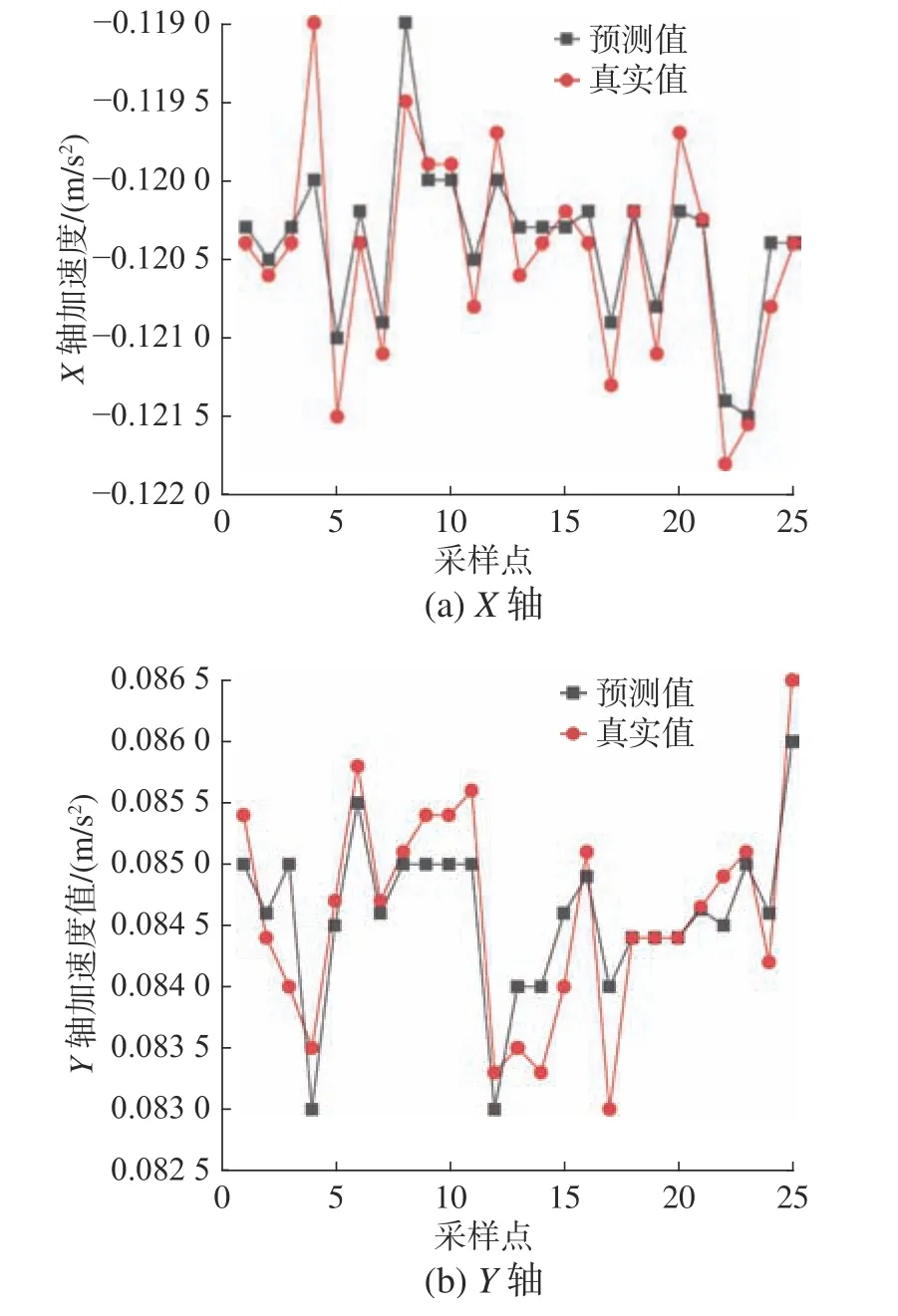
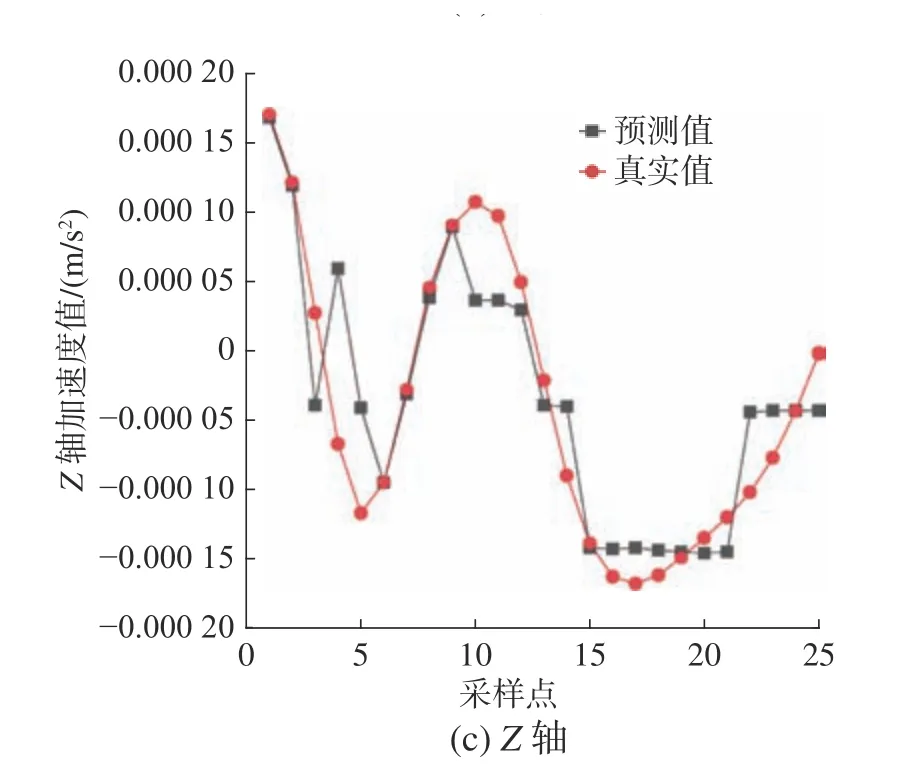
图5 组合模型在X, Y, Z轴上的预测结果Fig.5 Prediction results of the combined model on the X,Y, and Z axes

采用所建立的组合模型以2021年11月19日20时26分前25个采样点来预测精度，如图5所示，组合模型在X、Y、Z轴3个维度上的预测精度较高，效果很好，这一结果说明此模型预测精度较高。

同时本文也将循环神经网络(recurrent neural network, RNN)、长短期记忆网络(long short-term memory, LSTM)、门控循环网络(gated recurrent neural network, GRU)、双向循环神经网络(bi-directional recurrent neural networks, BiRNN）、双向长短期记忆网络(bi-directional long short-term memory,BiLSTM)、双向门控循环网络(bi-directional gated recurrent units, BiGRU)等传统预测模型作为竞争模型进行了比较，同时为了验证HHT法的贡献，考虑了部分竞争模型在HHT作用下的预测性能，得到预测误差结果如表4所示。

表4 预测模型结果对比Table 4 Comparison of prediction model results

相比较于RNN、GRU、双向RNN、双向GRU和LSTM等竞争模型，HHT+LSTM的RMSE分别下降了0.003 5、0.003 6、0.009 9、0.003、0.002 2；MAE下降了0.002 1、0.002 7、0.009 4、0.006 3、0.000 7；MAPE下降了73.4%、46.2%、229.9%、42.9%、22.2%。本文模型还与Informer进行了实验对比，但是从指标结果来看，Informer虽然是目前很流行的时间序列预测模型，但是对于本实验中真实数据集预测并没有达到很好的效果，反而本文提出的模型在各项指标中表现得十分出色，达到了很高的预测精度。证明了该组合模型较其他预测模型在临时设施运行趋势预测任务中更加具有可行性和有效性。

本文还将RNN、双向RNN和双向LSTM与HHT算法进行了结合，与本文提出的组合模型进行比较，综合表4结果来分析，证明了HHT与LSTM结合更加适用于此类任务，在预测精度结果方面具有更高的精度，效果更好。相比而言，本文提出的方法更有效地利用特征，并且根据表4中结果分析，HHT+LSTM性能优于其他传统预测模型，本文方法的综合性能也是最优的。算法中加入了时频分析的方法，使原始信号的信息更加丰富，预测算法的性能得到了很大改善。与传统的时频分析方法不同，HHT可以获得瞬时频率和幅度且不会产生频谱泄露，可以很好地刻画局部细节。通过将一维信号进行时频转换得到更加精细的二维的时频矩阵，丰富其特征。基于此引入LSTM有效地传递和表达长时间序列中的信息，并且可以解决梯度消失或梯度爆炸问题。将两者算法的优势结合，通过对比实验可以直观发现，本文提出的模型在临时设施预测方面具有一定的可行性和有效性，并比传统的预测模型表现得更加出色。不过，尽管该方法可以通过HHT时频图提供精细的信号信息，但相关模型训练所需算力也更大。

3.5 消融实验

本文进行消融实验以验证加入希尔伯特黄变换的有效性，实验结果如表5。本文在LSTM中先加入EMD模块时，实验效果反而降低。在加入了希尔伯特变换后，预测精度得到很大提升，评价指标也进一步的提升，证明了希尔伯特黄算法提升了模型的性能，提高了预测精度。

表5 消融实验Table 5 Ablation experiment

4 结束语

本文针对冬奥会临时设施运行趋势预测问题，提出了一种结合HHT和LSTM的方法，使用HHT来进行信号分解和提取时频域特征, 应用LSTM神经网络进行最终预测。本文通过运用HHT，将一维信号转换为二维时频图，可以更加深入地挖掘信号的时间和频率信息。通过利用LSTM可以有效解决长期依赖问题的优势来进行临时设施运行趋势预测。利用冬奥会现场真实数据集的验证，通过与多种传统预测算法进行比较，证明了本文方法具有一定的有效性和可行性。但相比而言，本文方法需要相对较大的算力，在未来的研究中会继续对其整体结构进行优化，提高其时频域分析方法的性能，并将其应用于其他领域。