一种多策略改进鲸鱼优化算法的混沌系统参数辨识

潘悦悦，吴立飞，杨晓忠

（1.华北电力大学 控制与计算机工程学院, 北京 102206; 2.华北电力大学 数理学院信息与计算研究所, 北京 102206）

在非线性科学领域，混沌系统的控制与同步是研究热点，其在信息科学、保密通信等方面应用广泛[1-2]，准确的混沌系统模型是实现同步控制的基础。然而，实际应用中，混沌系统结构复杂，部分参数不可知，因此精确辨识混沌系统参数具有重要的现实意义[3-4]。

近年来，许多学者开始关注和研究混沌系统参数辨识问题，并应用智能优化算法辨识系统参数。Chen等(2019年)[5]使用改进花授粉算法估计混沌和超混沌系统参数。数值模拟证明了新算法的有效性和鲁棒性。Ahandani等(2020年)[6]提出一种混洗复杂进化算法解决混沌系统参数估计问题，数值结果表明改进算法提高了参数估计的收敛速度和精度。Turgut等(2021年)[7]使用单元拓扑改进鲸鱼算法和正余弦算法，辨识混沌系统参数，测试结果证明，新算法成功地解决了参数识别问题。Ebrahimi等(2021年)[8]提出了一种改进洛兹映射混沌优化算法，数值结果表明，改进算法能够高效、准确地估计混沌系统参数。

鲸鱼优化算法(whale optimization algorithm，WOA)是一种新型群智能算法[9]，具有搜索能力强、计算稳定等特点，在最优控制、光伏系统等方面应用广泛[10-11]。然而WOA存在全局和局部搜索不平衡，易陷入局部最优等问题，因此国内外学者对WOA进行了有效的改进。Chen等(2020年)[12]提出一种准对立混沌WOA(whale optimization algorithm with chaos mechanism based on quasi-opposition, OBCWOA)，数值仿真结果证明了改进算法的全局搜索能力。Chen等(2020年)[13]为提高WOA的收敛精度和速度，提出一种双自适应随机备用增强WOA(reinforced whale optimization algorithm, RDWOA)。仿真结果验证了RDWOA的有效性。Chakraborty等(2021年)[14]为解决高维问题，结合多种策略，提出一种增强WOA(enhanced whale optimization algorithm, eWOA)，测试结果表明所提算法能有效解决高维问题。Shen等(2023年)[15]提出一种多策略进化WOA(whale optimization algorithm based on multi-population evolution,MEWOA)，试验结果证明了MEWOA求解优化问题的有效性。Deng等(2023年)[16]提出了一种具有多策略混合算法的改进WOA(improved whale optimization algorithm, IWOA)，仿真结果表明，IWOA有较好的收敛速度和稳定性。

以上改进算法虽然有一定提升，但在收敛精度和速度方面仍有待提高，本文在已有工作的基础上，以WOA为基础，使用Chebyshev混沌映射产生均匀分布种群，增加初始种群多样性。将收敛因子非线性化，增加自适应权重，兼顾全局搜索和局部挖掘。动态选择自适应t分布或蚁狮优化算法[17-18]，跳出局部最优。通过对10个基准函数和高维测试函数进行仿真试验，验证了MIWOA的优越性。将MIWOA应用于Ro¨ssler和Lu¨混沌系统参数辨识，仿真结果证明了MIWOA辨识混沌系统参数的有效性。

1 多策略改进鲸鱼优化算法的建立

1.1 基本WOA

WOA模拟了鲸鱼捕食行为，其仿生学原理描述如下：

1) 包围捕食阶段。

鲸鱼寻找食物时，当前鲸鱼根据最佳鲸鱼位置更新自身位置，公式为

式中：a=2-2t/T，t和T分别为当前迭代次数和最大迭代次数，X*(t)和X(t)分别为最佳鲸鱼位置和当前位置，r1、r2为[0,1]的随机数。

2) 螺旋更新阶段。

在螺旋更新位置时，鲸鱼通过螺旋向上的方式，靠近群体中最优位置，更新公式为

式中：D′为第i只鲸鱼和猎物之间的距离，b为改变螺旋形状的常数，l为[-1,1]中的随机数。

在鲸鱼搜索猎物时，收缩包围和螺旋更新同步进行，位置更新公式为

式中p为[0,1]之间的随机数。

3) 随机搜寻阶段。

鲸鱼通过|A|大小，选择随机搜寻或者包围捕食。当|A|＞1时，鲸鱼在包围圈外，通过随机搜寻获得猎物信息，位置更新公式为

式中Xrand为当前的一个随机鲸鱼位置。

1.2 WOA的改进

WOA初始化种群时采用随机搜索策略，全局搜索能力弱。包围捕食和螺旋更新阶段，收敛因子线性递减不能平衡全局和局部搜索。算法后期容易陷入局部最优。针对以上缺点，本文通过Chebyshev混沌映射初始化种群。包围捕食和螺旋更新阶段，非线性化收敛因子，加入自适应权重。算法后期，动态使用自适应t分布或蚁狮优化算法更新鲸鱼位置，对WOA进行改进。

1) Chebyshev混沌映射。

Chebyshev混沌映射对初值敏感[19]，可产生大量无周期实值序列。本文采用Chebyshev混沌映射对WOA进行种群初始化，迭代方式为

式中k为阶次。Chebyshev映射迭代1 000次的分布如图1所示。

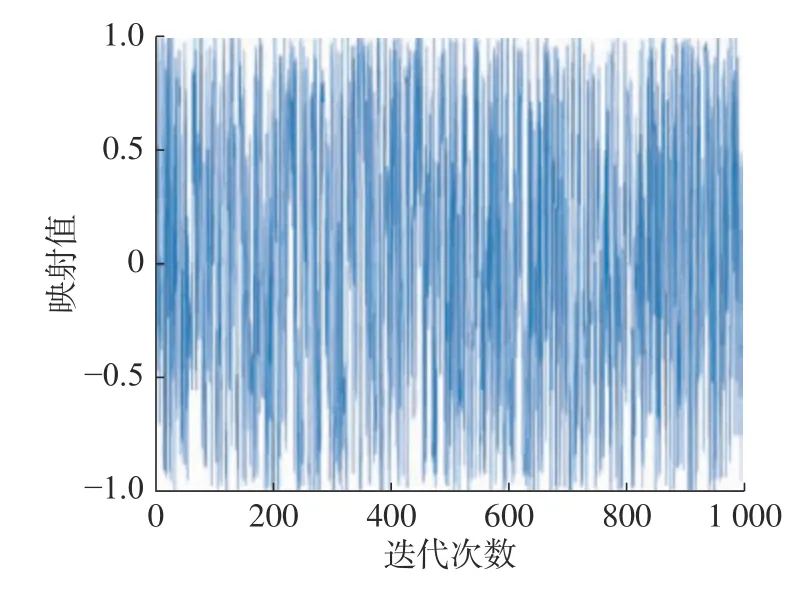
图1 Chebyshev映射分布Fig.1 Chebyshev map distribution

由图1可知，映射值分布于[-1,1]，Chebyshev混沌映射能更均衡地选取初始种群。将Chebyshev混沌序列映射到WOA解空间中，规定鲸鱼种群数为N，随机产生第1只鲸鱼个体向量，Y=(y1,y2,···,yd)。使用式(10)对Y的各维进行n-1次迭代，产生其余的n-1只鲸鱼。映射生成n只鲸鱼个体为

式中：ud和ld分别为搜索空间第d维的上下界，yid和xid分别为第d维的第i只鲸鱼和第i只鲸鱼的坐标值。

2) 非线性收敛因子和自适应权重。

WOA中，参数A∈[-a,a]调节全局搜索和局部挖掘。当|A|≥1时，算法进行全局搜索，当|A|＜1时，算法进行局部挖掘。随着迭代的进行，a=2-2t/T线性递减不能体现实际优化过程，因此改进收敛因子，公式为[20]

式中：u为大于零的常数，调节a的衰减程度。T=500时，图2为a随u的变化曲线。

图2 a的衰减曲线Fig.2 Attenuation curves of a

如图2，与WOA相比，u越大，a＞1所占的迭代次数比例越大，算法全局搜索能力越强，局部挖掘能力越弱。反之，u越小，a＜1所占的比例越大，算法局部挖掘能力越强，全局搜索能力越弱。所以a的变化趋势很大程度地影响优化求解。由于本文提出的Chebyshev混沌映射初始化种群策略，可以有效提高算法全局搜索能力，故选取u=0.6，增强局部挖掘能力，加快收敛速度，提高精度。

针对WOA后期局部挖掘时，权重固定，不利于算法寻优，本文提出一种自适应权重策略，公式为

3) 自适应t分布。

t分布又称学生分布，概率密度函数为[17]

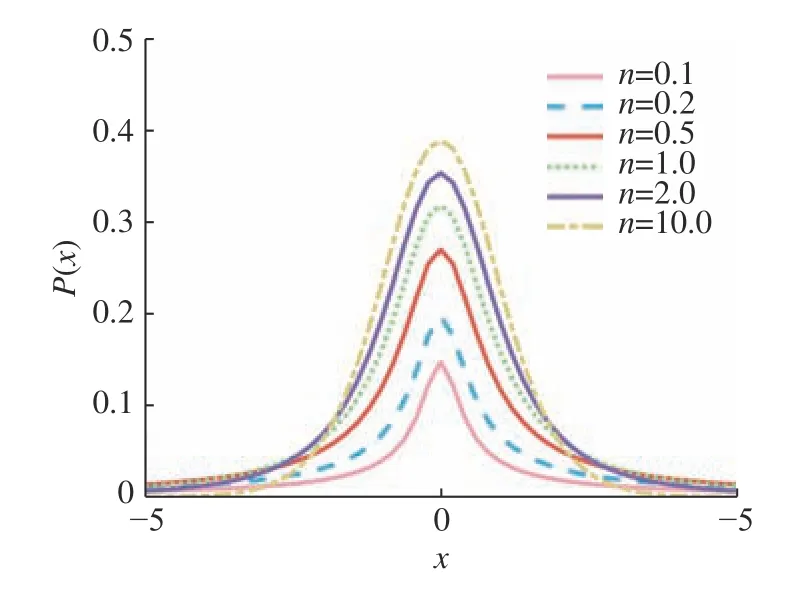
图3 函数分布对比Fig.3 Function distribution comparison

由图3可知，t分布的自由度n越小，曲线的双尾翘越高，中间峰值越小，整体越平滑。反之，自由度n越大，中间峰值越大，整体越陡峭。自适应t分布对鲸鱼位置的更新为

式中：xti为更新后的鲸鱼位置，n和t(n)分别为迭代次数和以迭代次数为自由度的t分布函数。

4) 蚁狮优化算法。

在蚁狮优化算法中，蚂蚁通过随机游走更新位置，公式为[18]

式中：cumsum为蚂蚁游走位置累加和，T为最大迭代次数，t为当前迭代次数，r(t)为0或1的随机数。蚂蚁随机游走公式的标准化形式为

式中：ai和bi分别为第i个变量的最小值和最大值，和分别为第t代第i个变量的最小值和最大值。

2 混沌系统参数辨识的MIWOA

2.1 混沌系统的参数辨识原理

混沌系统参数辨识原理如图4所示。

图4 混沌系统参数辨识原理Fig.4 Principle of parameter identification for chaotic system

考虑如下n维混沌动力学系统：

式中：x=[x1x2···xn]T∈Rn为系统的n维状态变量，x0为初始状态量，θ0=[θ10θ20···θm0]T为参数真实值。当辨识系统参数时，假设结构为

式中：y=[y1y2···yn]T∈Rn为辨识系统的状态变量，θ=[θ1θ2···θm]T为参数估计值。系统参数辨识是寻找一组最优未知参数，使系统真值x和估计值y的误差值最小：

式中：xk和yk分别为k时刻的系统真值和估计值，m为参数辨识状态变量序列的长度。目标泛函J(θ)的值越小，参数辨识的精度越高。MIWOA流程如图5所示。

图5 MIWOA流程Fig.5 Flow chart of MIWOA

2.2 MIWOA的时间复杂度分析

设种群规模为N，搜索空间维度为D，最大迭代次数为T，WOA的时间复杂度为O(NDT)。本文MIWOA以WOA为基础进行改进，Chebyshev混沌映射初始化种群的时间复杂度为O(ND)，非线性收敛因子和自适应权重未在基本WOA基础上增加循环嵌套，时间复杂度为O(NDT)，动态选择自适应t分布或蚁狮优化算法的时间为t1，则其时间复杂度为O(NDT+t1)，虽然MIWOA的时间复杂度相对WOA有所增加，但在可接受范围内，下面通过数值试验说明MIWOA的卓越性。

3 MIWOA性能测试与分析

3.1 测试函数的选取

仿真试验基于AMD Ryzen R7 5700U CPU@1.80 GHz，在Matlab R2019a 环境下运行。为了验证MIWOA有更好的寻优性能，选取表1的10个基准函数进行测试，ε表示绝对误差精度。f1～f7为单峰函数，f8～f10为多峰函数，10个测试函数的最优值均为0。

表1 基准函数Table 1 Benchmark functions

3.2 MIWOA与其他智能算法对比

采用10个基准函数检验MIWOA的性能，与WOA、粒子群算法(particleswarmoptimization，PSO)[21]、人工蜂群算法(artificialbee colonyalgorithm,ABC)[22]、灰狼算法(greywolf optimizer，GWO)[23]和哈里斯鹰算法(harris hawksoptimization，HHO)[24]进行测试结果比较。令N=30，D=30，T=1000，运行30次，表2为6种算法的最优值、最差值、平均值和标准差(黑色粗体为最优结果)。

表2 测试函数优化结果Table 2 Test function optimization results

由表2数据可知，对于单峰函数f1、f2，MIWOA的寻优结果均为0， WOA的计算结果优于PSO、ABC和GWO算法。在f3、f4测试函数上，MIWOA的计算结果优于HHO，可取得理论最小值。对于f5～f7函数，虽然MIWOA没有达到最小值，但优于WOA。对于多峰函数f8～f10，MIWOA可收敛到最优值附近，其中f9函数可收敛到最优值，说明MIWOA相对于其他算法有更好的收敛精度和稳定性。

基准测试函数的收敛曲线可以清晰地展现算法的收敛速度，图6(a)～(d)和(e)～(f)分别为单峰和多峰函数的平均收敛曲线。由图6可以看出，对于6个测试函数，在收敛精度相同的情况下，MIWOA收敛速度更快，说明Chebyshev混沌映射初始化种群策略提高了种群中高质量个体的比例，非线性收敛因子和自适应权重平衡了全局和局部搜索，加速收敛。MIWOA收敛曲线波动下降，说明自适应t分布或蚁狮优化算法的动态选择策略有助于算法跳出局部最优，提高收敛精度。

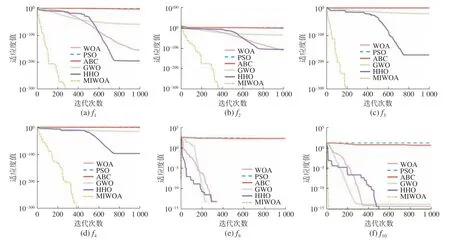
图6 30维测试函数的平均收敛曲线Fig.6 Average convergence curves of 30 dimensional test functions

3.3 Wilcoxon秩和检验

Wilcoxon秩和检验能够检测更为复杂的数据分布，并与算法多次运行的数据对比，公平地体现MIWOA的优越性[24]。实验设定显著性差异为5% ，当p＜5%判定两算法有明显差异，反之无明显差异。符号“＋”“-”和“＝”分别表示MIWOA的性能优于、劣于和相当于对比算法，N/A表示无法进行显著性判断。选取MIWOA在10个测试函数的运行结果与WOA、PSO、ABC、GWO以及HHO运行结果进行Wilcoxon秩和检验，计算p值。表3结果显示大部分p＜5%，说明MIWOA的寻优能力优于5种对比算法。

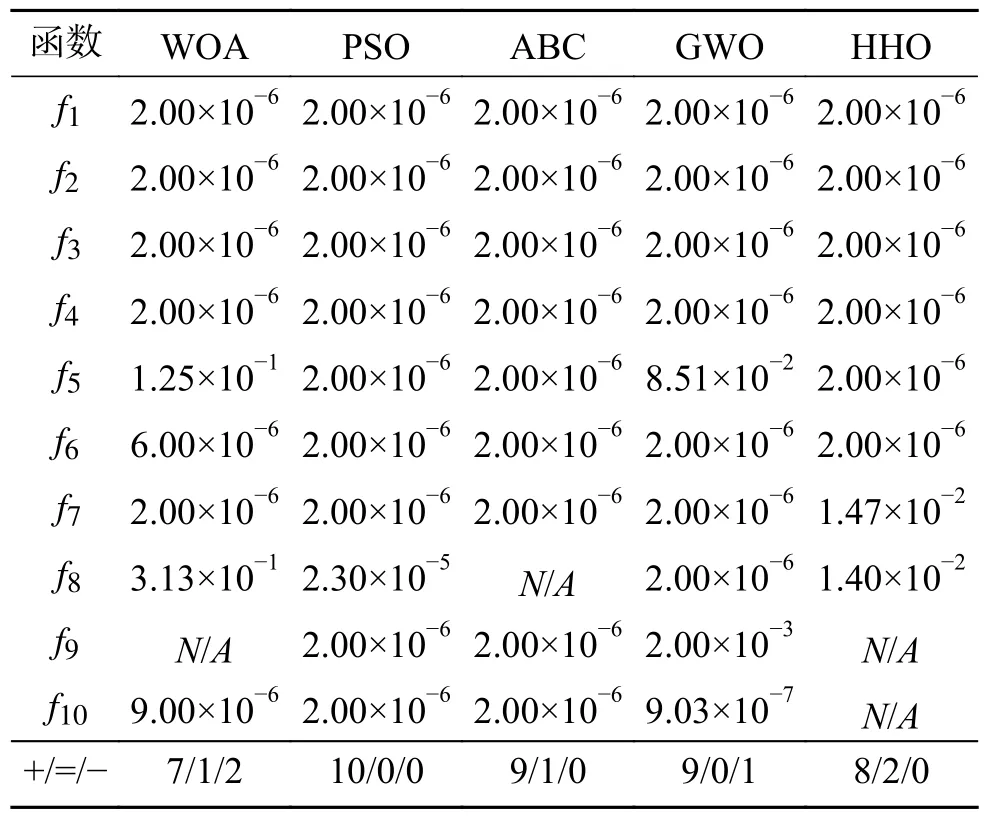
表3 Wilcoxon秩和检验结果Table 3 Results of Wilcoxon rank sum test

3.4 MIWOA不同改进策略的有效性分析

为比较3种改进策略对MIWOA性能的影响，令N=30，D=30，T=500，对f1～f10进行寻优计算，将MIWOA与WOA、WOA1(采用Chebyshev混沌映射)、WOA2(采用非线性收敛因子和自适应权重)和WOA3(采用自适应t分布或蚁狮优化算法)比较，计算结果如表4。

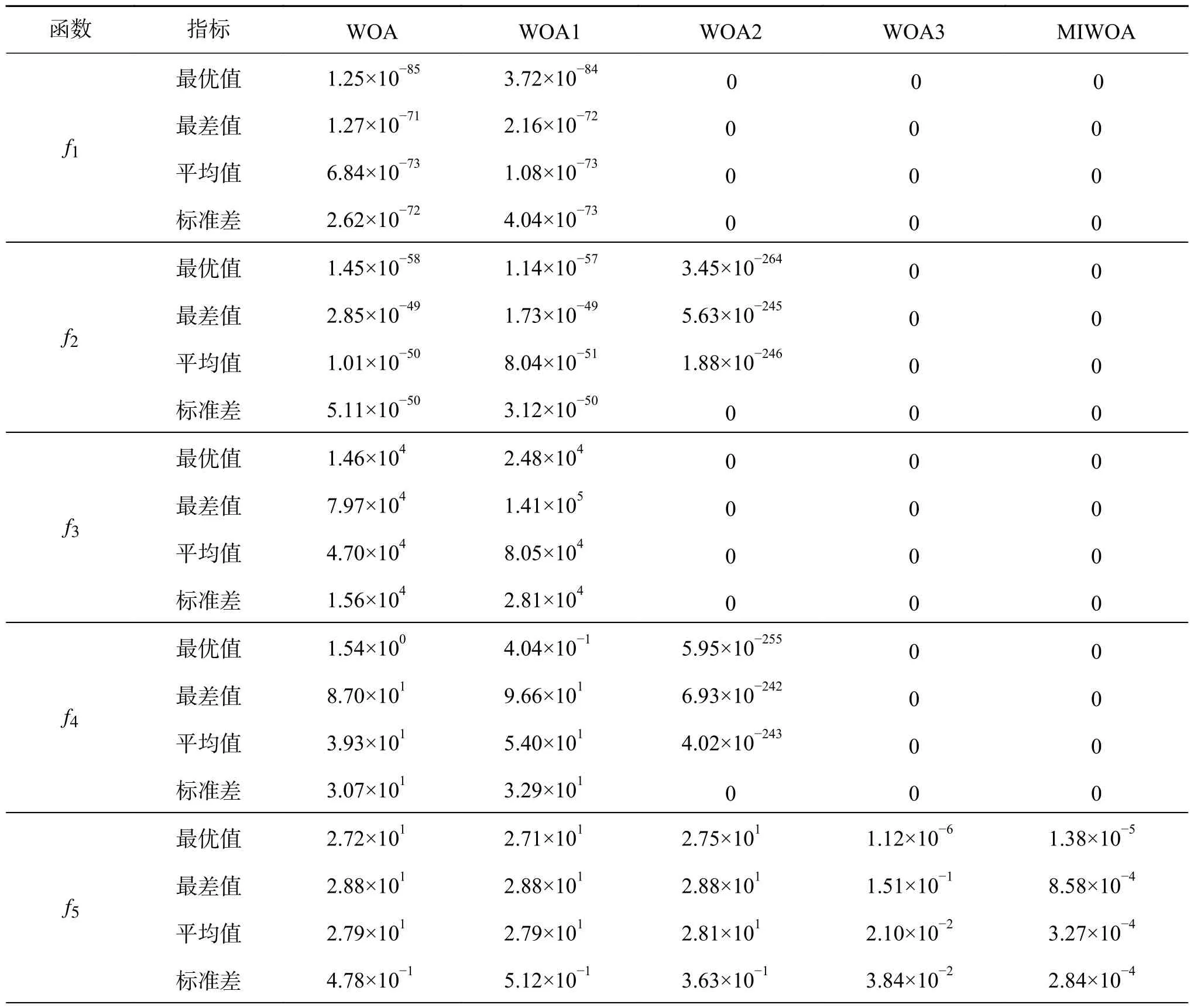
表4 不同改进策略算法性能对比Table 4 Performance comparison of algorithms for different improved strategies

由表4可知，3种改进策略对WOA均有不同程度的提升，WOA3的改进效果最好，WOA2次之，WOA1的计算结果低于其他2种算法的计算结果，但对WOA仍有明显的改进效果。将3种改进策略相结合时，算法搜索最精确，明显优于WOA1、WOA2和WOA3，表明3种改进策略是有效的。

3.5 MIWOA与不同策略改进WOA对比

为了对比MIWOA与其他改进WOA的改进效果，令N=30，D=500，T=500，引用3种算法(OBCWOA[12]、eWOA[14]和MEWOA[15])的数据，在相同测试条件下，对f1～f10测试，结果如表5。

表5 MIWOA与其他改进WOA性能对比Table 5 Performance comparison between MIWOA and other improved WOAs

表5结果显示，对于函数f1～f4，MIWOA与MEWOA可以在有限次迭代收敛到最优值，而OBCWOA和eWOA相对收敛精度较低。对于函数f5～f10，MIWOA可以使用更少的迭代次数收敛到最优值，说明MIWOA比其他改进WOA寻优效果更好。

平均绝对误差(meanabsoluteerror, MAE)是评价算法有效可行的重要指标，计算公式为[23]

式中：mi为算法求解结果平均值，oi为各测试函数理论值，Nf为测试函数个数。表6为除理论值非零的f8函数外，4种算法的MAE排序，由计算结果可知，MIWOA的MAE值最小，排名第1，证明了本文改进策略的有效性。

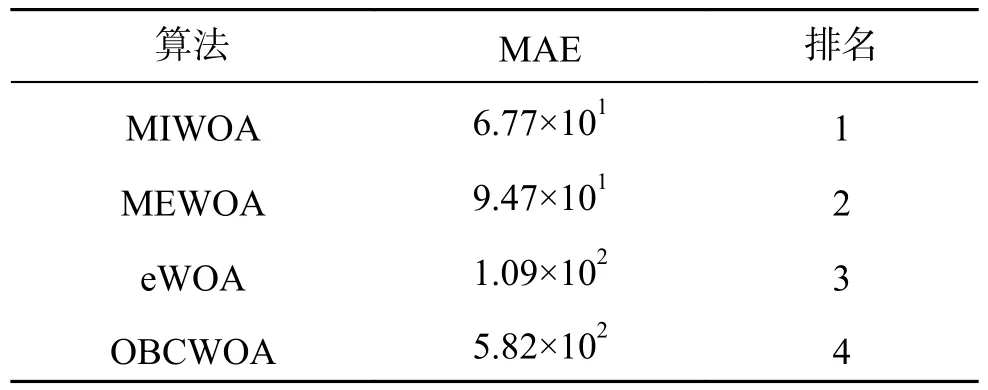
表6 4种改进WOA的MAE排名Table 6 MAE ranking of four improved WOAs

3.6 MIWOA求解高维函数的实验分析

由上述计算结果可知，对于低维测试函数，本文MIWOA寻优效果良好，但实际应用中高维大规模问题普遍存在，为了检验MIWOA求解高维问题的可行性，将其在10个基准函数，N=30，T=500，D=200、500、1000情况下，运行30次取平均值，根据文献[25]求解算法寻优成功率。绝对误差精度如表1所示，计算结果如表7。

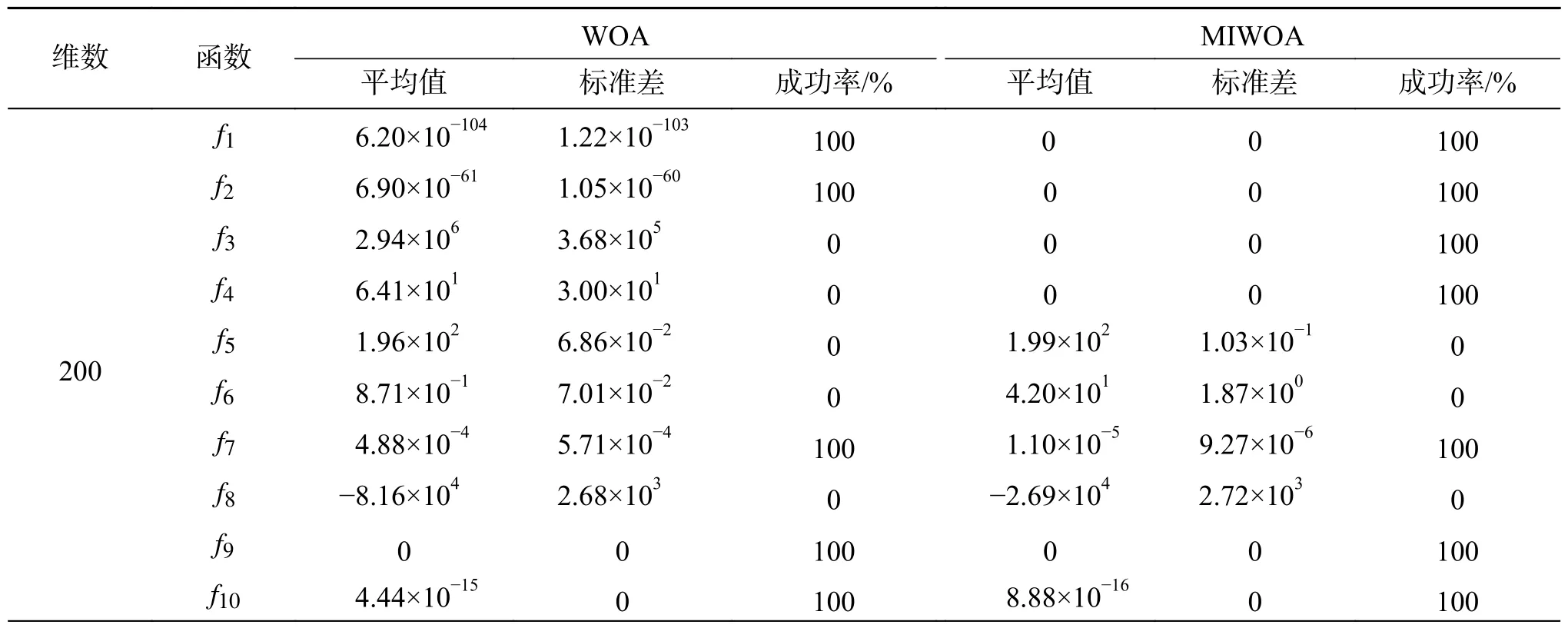
表7 高维测试函数优化对比Table 7 High dimensional test functions optimization comparison

从表7可以看出，两算法在求解高维测试函数时，寻优精度比求低维函数略有下降，但整体仍可达到较高精度，获得理想结果。MIWOA在7个基准函数上寻优成功率达到了100%，相同维度下，MIWOA的寻优效果比WOA更好，说明MIWOA对于求解高维优化问题具有较高的计算精度和稳定性。

3.7 MIWOA平均运行时间分析

为了验证MIWOA的计算速度，将其与PSO、ABC、GWO、HHO、WOA、WOA1、WOA2、WOA3运行30次的平均时间对比，N=30，D=1000，T=500，计算结果如表8。

表8 基准函数寻优平均时间对比Table 8 Comparison of average time for optimization of benchmark functions

由表8可知，对于元启发式算法，WOA与ABC、HHO运行时间相近，可以快速收敛到最优值。对于改进算法，WOA、WOA1和WOA2的平均时长相当，说明WOA1和WOA2的改进策略未增加WOA运行时间。由于算法后期动态选择自适应t分布或蚁狮优化算法，增加了循环嵌套，WOA3耗时多于WOA。融合多种改进策略的MIWOA搜索范围变广，寻优时间增加，但均在合理范围内，与理论分析相符。

4 MIWOA辨识混沌系统参数

4.1 MIWOA对Ro¨ssler 混沌系统的参数辨识

Ro¨ssler 系统具有简单、非对称吸引子结构，在保密通信中承担非常重要的作用。以典型Ro¨ssler混沌系统为例，验证MIWOA可以精确辨识混沌系统参数。Ro¨ssler系统表达式为[7]

当参数a=0.2，b=0.2，c=5.7时，系统为混沌状态，其演化过程如图7所示。令初值向量为[-101]T，步长h=0.01，使用四阶Runge-Kutta法解式(21)，利用前100个解及PSO、WOA、MIWOA辨识待定参数[abc]T，各算法独立运行20次。

图7 Ro¨ssler 混沌系统动力学轨迹Fig.7 Dynamic track of Ro¨ssler chaotic system

首先测试3种算法在具有一个未知参数的Ro¨ssler系统参数辨识中的搜索性能，即每次只辨识a、b、c3个参数中的一个，测试结果如表9。由表中数据可知，对于参数a，MIWOA可收敛到理论最优值，其最差值优于其他2种算法的最优值。对于参数b，WOA和MIWOA均可达到理论最优值，但MIWOA寻优效果更好。对于参数c，MIWOA的适应度值小于PSO和WOA的适应度值，估计值很接近真实值，说明MIWOA具有良好的全局搜索能力和计算鲁棒性。

表9 不同算法的一维参数估计结果比较Table 9 Comparison of one-dimensional parameter estimation results for different algorithms

然后测试各算法在具有2个未知参数的混沌系统参数辨识中的搜索性能，计算结果如表10。从表10估计a和b可以看出，各算法搜索精度相似，相对于一个未知参数的情况，搜索精度略有下降，但MIWOA的计算结果仍优于PSO和WOA。另外2种情况也得出同样的结论，验证了MIWOA辨识2个未知参数Ro¨ssler系统的可行性。

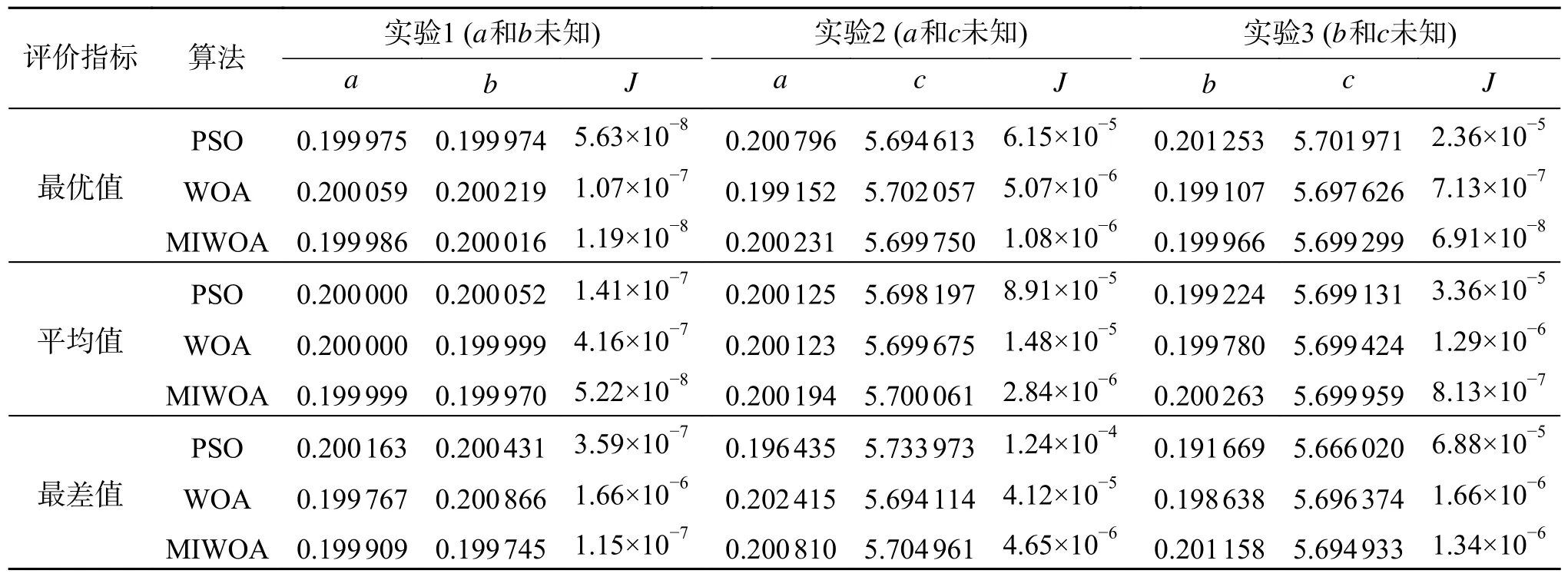
表10 不同算法的二维参数估计结果比较Table 10 Comparison of two-dimensional parameter estimation results for different algorithms

最后，使用3种算法辨识具有3个未知参数的混沌系统，表11为各算法运行20次的统计结果。由表11中数据可知，各算法的搜索精度下降，但MIWOA的最差值优于PSO和WOA的最优值，在3种算法中搜索精度最高，表明MIWOA对Ro¨ssler混沌系统参数辨识更具有效性。

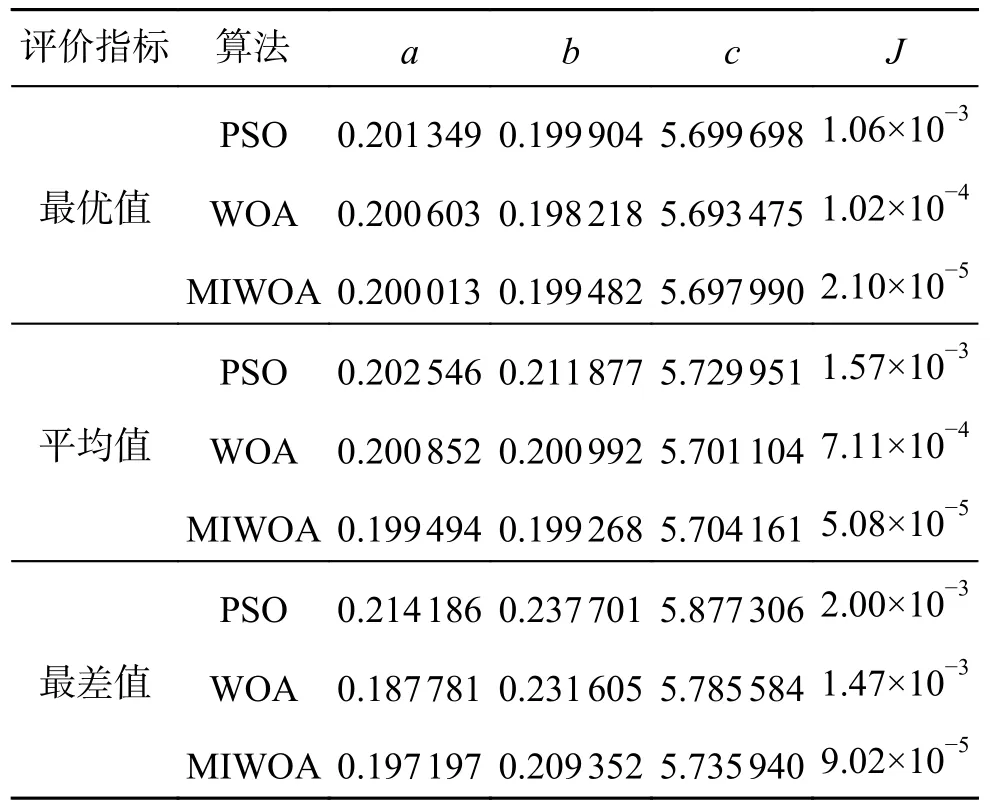
表11 不同算法的三维参数估计结果比较Table 11 Comparison of three-dimensional parameter estimation results for different algorithms

图8和图9分别是WOA和MIWOA对Ro¨ssler混沌系统的参数辨识曲线和适应度值曲线，从图中可以看到MIWOA的参数估计值可以快速收敛到真实值，适应度值迅速逼近0，表明MIWOA高效的全局搜索能力和快速收敛速度。

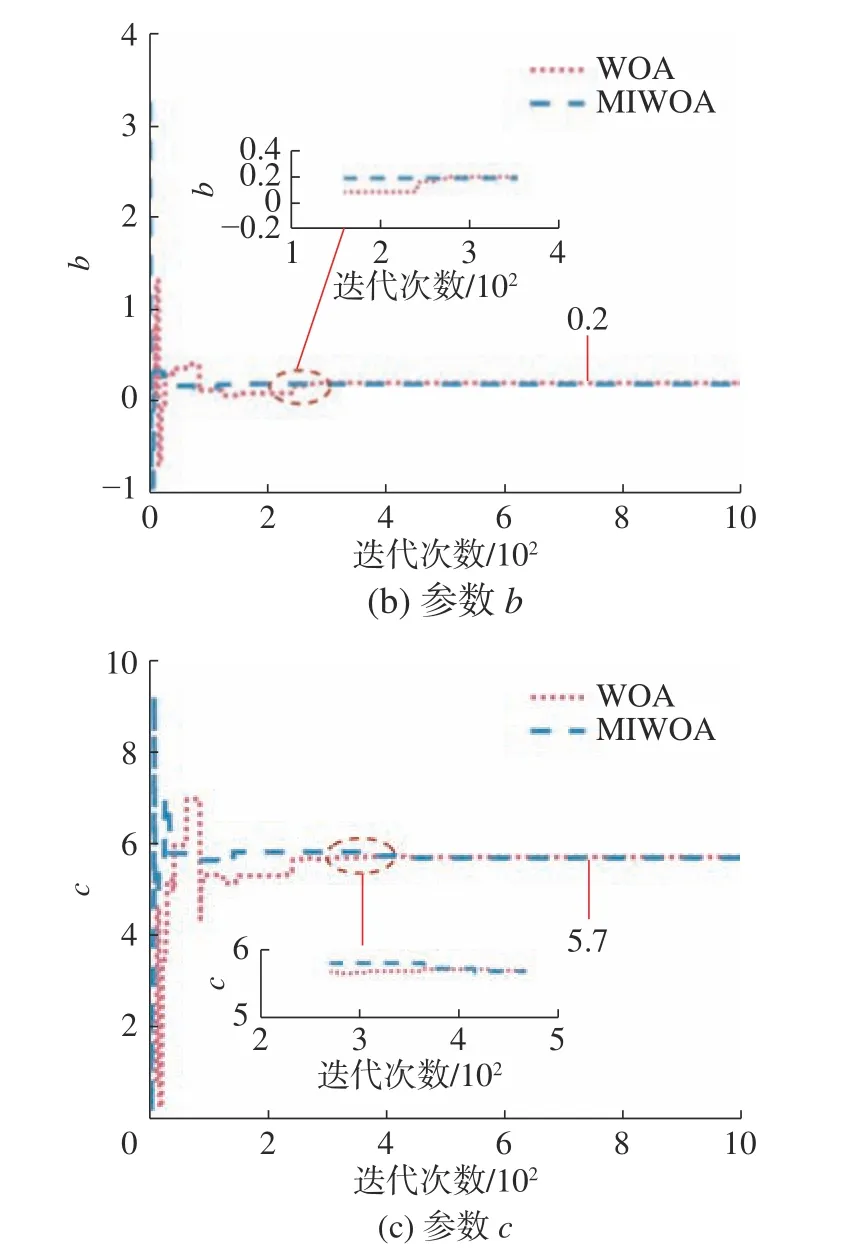
图8 WOA和MIWOA参数辨识曲线Fig.8 Parameter identification curves of WOA and MIWOA

图9 WOA和MIWOA适应度值曲线Fig.9 Fitness value curves of WOA and MIWOA

4.2 MIWOA对Lu¨ 混沌系统的参数辨识

为了验证MIWOA对混沌系统参数辨识的普适性，以Lu¨系统为例进行仿真，表达式为[26]

其中，系统参数真实值为a=30，b=22.2，c=8.8/3时，系统为混沌状态，其演化过程如图10所示。

图10 Lu¨混沌系统动力学轨迹Fig.10 Dynamic track of Lu¨ chaotic system

令初值向量为[-101]T，使用PSO、WOA和MIWOA辨识Lu¨混沌系统3个参数未知时的情况，3种算法独立运行20次，辨识结果如表12所示。

表12 各算法的三维参数估计结果比较Table 12 Comparison of three-dimensional parameter estimation results for each algorithm

由表12中数据可知，除了MIWOA的最优适应度值大于WOA的最优适应度值，MIWOA的计算结果均优于其他2种算法，说明MIWOA辨识混沌系统具有普适性。

5 结束语

本文以WOA为基础，提出一种MIWOA。通过分析初始种群分布，使用Chebyshev混沌映射提高了初始种群质量。采用非线性收敛因子和自适应权重，提高了算法全局和局部搜索能力。动态选择自适应t分布或蚁狮优化算法更新鲸鱼位置，避免过早收敛。通过对10个基准函数和高维测试函数进行测试，以及Wilcoxon秩和检验，证明了MIWOA的优越性。

将MIWOA应用于Ro¨ssler和Lu¨ 混沌系统的参数辨识，仿真结果优于PSO和WOA，验证了MIWOA辨识混沌系统参数的高效性。今后将继续研究WOA的优化策略，将其应用到混沌系统控制与同步等其他领域。

致谢本文作者衷心感谢德国阿尔弗雷德韦格纳研究所 Sergey Danilov 教授和王强博士在写作过程中提出的宝贵建议和意见！