冲刺阶段，高考数学的破局策略 高考有变！ 今年数学“新”在哪？

廖国达

上个月，随着湖北、江苏、广东、山西、重庆等地陆续发文采用新的试卷结构进行“新高考”。通过调整试卷结构，力图实现能力考查的目标，助力拔尖创新人才的选拔和培养。我们要深入理解改革方向，分析改革措施，做好教学和复习备考。

新旧试卷结构对比

下文，我们深入研究本次题型和题量的变化。

1.题型和题量变化

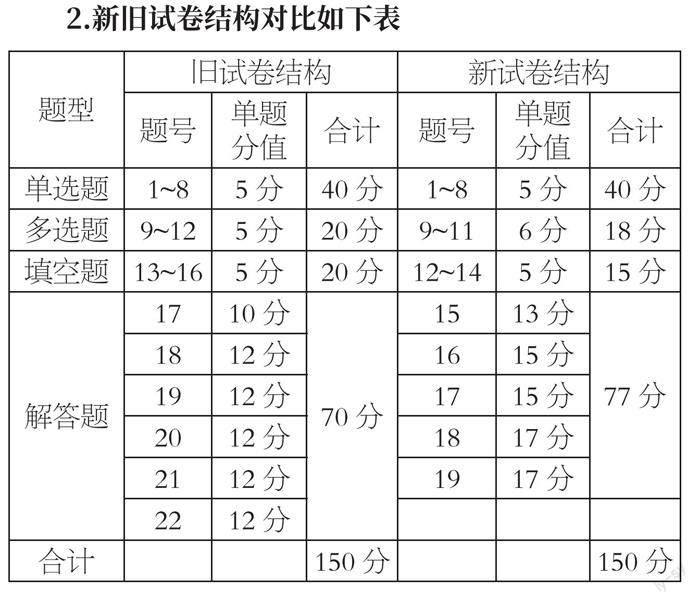
题型由原来的“8+4+4+6”，变成“8+3+3+5”：多选题由4道变成3道，填空题由4道变成3道，解答题由6道变成5道。试卷的总分值仍为150分，但选填题的总分值由原来的80分变成73分，解答题的总分值由原来的70分变成77分。

2.新旧试卷结构对比如下表

3.单选题题量和分值不变

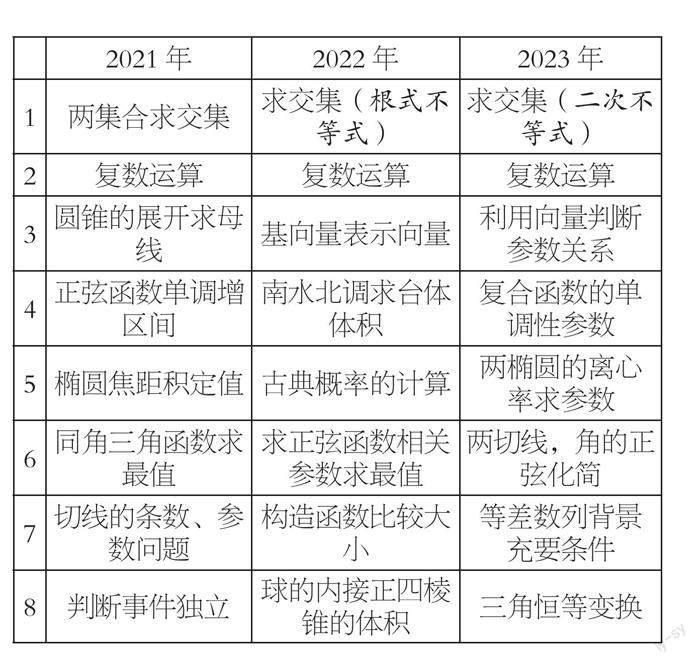
单项选择：8小题共40分，与原来保持不变。下表是近三年的考点分布。

4.近三年单选题考点分布分析

近三年，试卷1～8题考点分布较为稳定，整体上内容聚焦于集合常用逻辑用语、平面向量、复数、三角函数、数列、立体几何、概率统计、解析几何等部分。

今年选择题和填空题的考查知识点的顺序可能有变化，例如考查集合知识点的题目可能由之前放在选择题第1题或第2题，变到填空题第1题的位置。再如，考查复数知识点的题目可能由选择题改为多选题。但是，“稳定”地坚持对基础知识、基本技能和基本方法的考查，坚持对学生的理性思维能力的考查。

5.多选题减少一题，每题分值提高

三道多选题共18分，题量比往年减少1题，每题分值由5分提高到6分。多选题的题量减少，给分方式也发生了改变：有可能是若两个选项正确，每选对一个给3分；若3个选项正确，每选对1个给2分，错选不给分。这种新的给分方式，显然更符合“新高考”加入多选题的初衷——多思考、多辨析、多计算。选对全部选项的难度增加，这有利于将水平较高的考生区分出来。在此，提醒考生认真阅读题干，清楚得分细则。

6.填空题减少一题，总分值降低

去年全国Ⅰ卷第13题考查组合数的计算，14题是求棱台的体积，15题是已知函数零点的个数求参数的取值范围。答填空题时，注意答案必须是准确的数值，且保证形式规范，稍有不慎，就不能得分。

7.解答题题量减少，分值提高

五道解答题共77分，比往年减少一道题，但总分值增加。高中数学的六个重要板块，分别是三角函数、数列、导数、立體几何、解析几何、概率统计，解答题“减量”意味着无论哪一个板块没有出现在试卷中，都是正常现象。但我们不要妄自总结“经验”，盲目推断某个内容可能不考，而是要全面复习各项内容，有备而战。同时，题量减少以后，每道题的分值增加，解答题的重要性显著提升。

“新高考”如何破局

“新高考”主要考查考生的思维方式和探究技能，重视考生的逻辑推理能力、数学抽象能力、空间想象能力、数据处理能力、快速准确运算能力。破局关键仍是拿全、拿好基础分。

1.强化基础知识

无论题型如何变化，基础知识始终是解题的关键。针对基础知识的备考，要做到两点。

第一，从教材到高考。平时训练的试题要大多数来源于教材，以便更好地检测复习中对基本概念、原理、思想方法的掌握情况。

第二，我们要加强历年高考真题训练，特别是考查以下知识点的题目：集合、复数、等差和等比性质、三角函数的图象、函数（抽象函数、函数图象、函数零点、简单的比较大小）、立体几何、向量的平行与垂直（图形特殊化坐标法）、直线与圆、二项式定理、概率统计的概念。

2.注重解题技巧

除了基础知识，解题技巧也是解题的关键。掌握一些选择题压轴题或多选题的解题方法，如排除法、特殊值检验法、极端性原则、顺推破解法、逆推验证法、正难则反法、数形结合法、递推归纳法、特征分析法、估算法。要注意灵活运用方法，因为很多情况下，都不是使用方法就能解题，而是需要学生穿插综合运用多种方法解题。

在复习过程中，注重培养解解答题的技巧，尤其是针对分值在15分、17分的新题型，要了解其得分点。例如，考查圆锥曲线的题，得分点是由概念得出圆锥曲线方程、作图标点、斜率公式、斜率不存讨论、直线方程、垂直转化向量、两点间距离与弦长公式、角度转化斜率问题、直线方程代入曲线方程、运算交点坐标、韦达定理、化归统一变量，平时要好好把握这些得分要点。再如解函数、导数题，按“定、导、分（分解因式、分离参数、分类讨论）、构（构造函数、三构三导）、图、综（结合分析）”六字诀，尽量夺分。

3.保持积极心态

面对新题型，师生们可能会感到一些压力和挑战。但重要的是保持积极的心态，相信自己的能力和努力，相信通过复习和训练，一定能够应对新题型的挑战。试卷题量减少，有利于考生稳拿80分，利好体艺生、文科生，这类考生要有良好的心态，在单选题中充分展现自己的水平，在多选题中多要分，认真做好前两道填空题，认真准备解答题的前三道题。

不同分数段考生如何冲刺

1.平时80～120分的考生

（1）提升关键能力

高考重点考查学生的逻辑推理能力、数学抽象能力、直观想象能力，所以要有意识地提升关键能力。

（2）调整复习计划

80～120分之间的考生，基于对“新高考”的研究，需要调整原有的复习计划，当然，由于解答题分值增加，给分可能就会更加详细，所以考生需要更加注意解答题的规范表达，核心步骤不能跳跃，尽可能避免一些不必要的丢分。可能需要对以下三道解答题进行重点训练，提高解题速度（每题10分钟内完成）。

第一道：立体几何题——考查推理能力、空间想象能力。前几年的立体几何解答题，建系过程都不是那么显然，需要考生分析空间位置，找到合适的垂直关系来实现。高考复习应该把握近年的命题变化，从以下三方面入手。第一，提升几何论证能力，传统法先行，向量法要有建系过程的论证，需要严谨表达；巧用墙角、长方体、对称来建系。第二，过好运算关，要巧算，能熟练借用平行、垂直、对称、特殊图形的性质来确定点的坐标和相关向量，注意巧用平行向量进行去分母、有理化、化单位向量等方法简化相关向量后求法向量。第三，多去研究往年立体几何真题中最佳解题策略，如2023年全国乙卷用向量的基底法求解空间角。

第二道：函数导数题——考查独立思考、探索、创造性地解决问题能力。今后导数复习需重点关注求参数的取值范围、分类讨论、零点问题、单变量函数不等式的证明，等等。平时要多加训练分离参数的方法、分类讨论和假设反证的方法。

第三道：概率统计题——考查阅读能力与数据处理能力。高考概率统计题，要重视互斥事件、独立事件求概率，同时也要注意用概率进行决策的试题。要重视往年考查方向是经验回归方程相关的真题，能在实际情境中从数学的视角发现问题、提出问题、建立模型、检验结果、改进模型。要重视概率统计与数列结合的题型，例如传球模型、药物模型、摸球模型、游走模型等题型。

（3）增加模拟训练

面对数学“新高考”，模拟训练是检验复习效果的有效方法。在第二轮复习中，应该增加模拟考试的频率，以下是一些建议，希望能帮助考生更有效地进行模拟训练。

第一，选择合适的模拟题。例如武漢、深圳的模拟题，素有“高考风向标”之称。

第二，定时完成模拟训练。模拟考试应该尽量模拟真实考试的环境，建议在下午3点至5点内完成。

第三，分析错题。完成模拟考试后，务必对错题进行深入分析，同时，也要关注自己在解题过程中展现出的优点，保持自信。

第四，定期进行模拟训练。建议每周至少进行一次模拟考试，以保持手感和解题能力。

总之，进行模拟训练是应对数学“新高考”的关键环节。通过选择合适的模拟题、定时完成、分析错题、总结经验、制订复习计划以及保持良好的心态，更好地应对“新高考”的挑战。

2.目标在120分以上的考生

（1）提升关键能力

高考重视对考生能力的考查，说实话，目标在120分以上的考生肯定都具有很好的学习思维习惯，在冲刺阶段，需要关注以下三类题目。

第一，选择题和填空题的压轴题。考查化归与转化能力，发展直观想象、逻辑推理等能力。压轴小题基本是考查函数、数列、导数、解析几何、立体几何等知识，但在此也要提醒考生，各板块的必备基础知识都有可能作为压轴题来考。创新题不一定是解答题，也可能是选择题与填空题！

第二，解析几何题。考查分析问题、确定参数、建立模型证明不等式等探究能力。2021年和2022年以双曲线为考查背景，延续全国卷的命题风格，均是一些熟悉的模型，例如斜率和、斜率积、阿基米德三角形，等等。去年全国Ⅰ卷把圆锥曲线作为最后一题，既打破了传统圆锥曲线的地位，同时又不像往年那样是结论性问题，算是一种创新。

第三，第19题——创新题（17分）。对考生的综合素质和临场应变能力提出极高的要求，需要考生具备信息提取加工能力、数学符号的理解和推导能力，是一个从具体到抽象、从一般到具体的科学探究过程。今年的第19题大概率会是基于课标内的六大核心素养的创新题，可能涉及新定义问题、类比与归纳、探究与拓展、数学建模等内容。

（2）深入研究新题型

逐步创新是高考的大方向，创新的试题每年有，今年要特别关注。创新的试题可能不会再像往常，是一道导数、解析几何压轴题，而是融合了数学情境、数学背景，需要数学建模、数学抽象等素养的综合题，更有可能是多个板块的融合。例如往年出现过的椭圆曲线、密码学问题，下次会不会是人工智能里面的“维度灾难”？一切皆有可能。考生可以在第二轮复习中选择相应的习题来接触、学习、适应，其中北京、上海的相关试题值得去研究。

（3）寻求专业指导

如果师生在复习过程中遇到问题或困惑，可以寻求专业的指导——把握方向、知己知彼、科学备考、高效学法。新结构下解答题单题分值的提高，必将对答题规范提出更高的要求，特别是目标在120分以上的考生更要寻求专业的指导，指导思维细节、答题规范，对于有把握做的题，呈现要更完美，一分都不能丢。

总之，在今年试卷结构大改的背景下，难度大概率会维持在去年的水平。高考只设置五道解答题，比原结构少了一道，不要去猜测是少了哪一个模块的内容，复习还是要把传统的六大模块都照顾到。夯实基础，多回归课本，以课程标准为准；多研究往年高考真题，以高考评价体系为纲，才能主动、高效地学习，以不变应万变，自信从容地应考。