基于L1制导的巡飞弹航迹跟踪技术
王帅为,王荣刚,王嘉文,梁益铭
(西安现代控制技术研究所,陕西 西安 710065)
0 引言
巡飞弹是现代信息战多技术融合的智能化精确制导武器,可对目标区域上空实施侦察、监视压制并可自主根据战场态势进行制导,网络协同化、小型智能化和低成本是其未来发展的主要趋势。自1994年美国开始研制低成本自主攻击弹药以来,巡飞弹就在世界弹药及制导武器领域引起了广泛关注[1-4]。随着巡飞弹的广泛应用,要求巡飞弹对规划出的航迹进行准确跟踪,实现对任务区域的精确、全面覆盖[2]。Sujit等[4]对比分析了实现较易、鲁棒性强的常用航迹跟踪算法,并将其思想总结为5类:虚拟运动目标法[5-6]、视线导引法[7]、线性二次型法[8]、向量场法[9]。前3类方法的鲁棒性受风扰动影响,且存在较大的横向偏差;向量场法横向误差最小,但需调整的参数较多,并存在抖震现象。而传统的航迹跟踪算法多采用PD控制,鲁棒性差,且当航迹误差较大时,易产生超调,因此需要研究一种新的简单易行的航迹跟踪算法,在减轻弹上计算机压力的同时,提高巡飞弹在复杂环境下的航迹跟踪能力。
文中针对巡飞弹航迹跟踪问题提出了一种基于L1制导的航迹跟踪方法,实现了巡飞弹对直线航迹和圆航迹的无超调跟踪,并通过数字仿真证明了此方法的有效性。
1 L1航迹跟踪
L1制导法的基本原理是:在跟踪航迹上选择一点,作为虚拟目标跟踪点,该点距巡飞弹M距离为L1。令巡飞弹做圆弧运动,逼近虚拟目标点T[3]。过载指令为:
(1)
式中:V为巡飞弹速度;R为圆弧轨迹半径。

图1 L1制导轨迹Fig.1 L1 guidance trajectory
由几何关系可知:
L1=2Rsinη
(2)
式中η为弹目连线与速度方向的夹角。
代入式(1)可得:
(3)
式中K为导航系数。L1制导法的主要问题是η如何确定。
当η比较小时,sinη和ay可表示为:
(4)
式中:η1为巡飞弹速度与参考航迹的夹角;η2为弹目连线与参考航迹的夹角;d为巡飞弹距参考航迹的距离。
忽略内环动力学,制导律可以写成:
(5)
由此可知,采用L1制导法跟踪直线航迹系统等效于如下一个标准二阶系统:
(6)
式中:wn为制导加路带宽;ξ为阻系比。
若选择K=4,系统的自振频率和巡飞弹速度与L1有关,阻尼比为1,可等效为无超调二阶系统。巡飞弹一般采用BTT控制,侧向运动由滚转角控制,即nz≈γ。设滚转通道带宽为wr,可选择wn≈kwr。k取1/2~1/3。又设滚转角最大限幅为γmax,可确定的最小转弯半径为Rmin。故L1参数可由最大滚转角和滚转带宽确定。

图2 滚转通道控制框图Fig.2 Roll channel control block diagram
2 航迹跟踪
巡飞弹在巡飞中主要技术动作包括爬升、俯冲、巡飞、左盘、右盘等,而与平面航迹有关的只有巡飞、左盘和右盘。故可将航迹跟踪分解为直线跟踪和圆航迹跟踪[10]。
为了实现L1制导律,需确定巡飞弹的巡航速度、导航系数、L1参数及前置角。其中,巡航速度可利用弹上惯导获得,导航系数和L1参数可利用上一节中的方法获得,实现的关键是前置角如何获得。下面针对圆形航迹和直线航迹分别进行讨论。
2.1 圆形航迹
当期望轨迹为圆时,根据巡飞弹与圆心位置,可分类讨论。巡飞弹当前位置与航迹圆的距离d可表示为:
(7)
式中:x0,y0为航迹圆心位置;x,y为巡飞弹当前位置。
1)若d≥R0,如图3所示,R0为航迹圆半径,M为巡飞弹当前位置,M1为过当前位置圆的切线与圆的交点。V为巡飞弹速度向量,η2为V与向量LMO的夹角,η1为向量LMM1与向量LMO的夹角。则η可由式(8)确定。
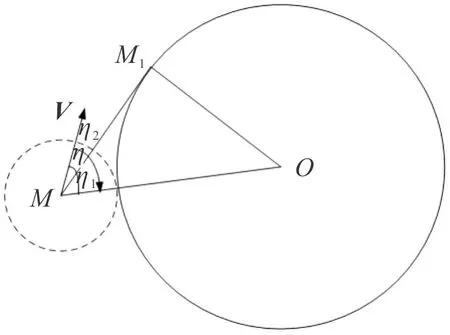
图3 巡飞弹在航迹圆之外Fig.3 Outside the course circle

(8)
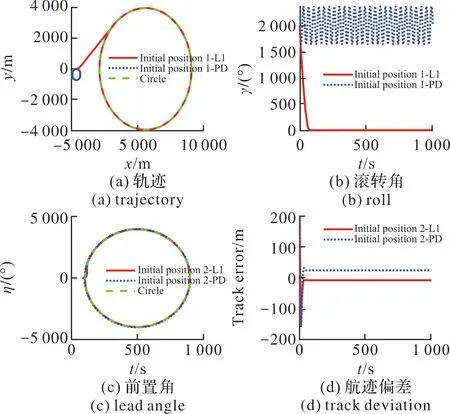
2)若d 图4 巡飞弹在航迹圆之内Fig.4 Loitering missice within the course circle η=0 (9) 3)若R0>d≥(R0-L1),如图5所示,LG1向量指向L1圆与参考圆的交点。则η由式(10)确定。 图5 巡飞弹与航迹圆相交Fig.5 Loitering missice intersects the course circle (10) 如图6所示,当期望轨迹为直线时,根据巡飞弹与航路的位置,可分类讨论。 图6 直线航迹Fig.6 Rectilinear course 巡飞弹当前位置M与A1航路点的距离可分别表示为: (11) 1)若巡飞弹满足: (12) 则选择LG1向量指向A1点。 (13) 2)若巡飞弹满足: |d|≤L1且cosθMA1A2≥0 (14) 则选择LG1向量指向L1圆与航迹交点。 (15) 3)若巡飞弹满足: |d|≥L1,cos(θMA1A2)≥0 (16) 则选择LG1向量沿航迹法线方向指向航迹曲线,η1,η2,η可表示为: (17) 图7 切换航迹Fig.7 Switch course 当前航迹与下一航迹的夹角Δη和切换距离dq可表示为: (18) 设切换航迹为一段圆弧,半径R可表示为: (19) 式中:Rmin由最大滚转角确定;wn为制导回路带宽。 对提出的L1制导律进行仿真验证,巡飞弹方程组参考文献[11]。对于圆形航迹,矩形航迹,五角星航迹分别进行跟踪。设巡飞弹速度为60 m/s,滚转角限幅45°,初始弹道偏角为0。航迹圆半径为R0=4 km,圆心位置为(5 km,0 km)。矩形和五角星航迹的中心均为(0,0),中心距顶点的距离均为5 km。针对巡飞弹不同初始位置,进行仿真验证。仿真结果如图8~图10所示。采用传统的PD控制进行对比,结果如图11所示。 图8 圆航迹跟踪Fig.8 Circular course tracking 图8为跟踪圆形航迹。由图8(a)和图8(d)可以看出,无论巡飞弹初始位置在何处,最终都收敛于理论轨迹,且无明显超调。由图8(b)和图8(c)看出,在初始误差比较大时,滚转角和前置角较大,但最后均趋于稳定。 图9和图10为跟踪直线航迹。由图9、图10的(a)和(d)可以看出,巡飞弹均可以无超调的跟踪直线航迹。两段直线航迹夹角越小,转弯的提前量越大。由图8、图9的(b)和(c)可以看出,只有在转弯段,滚转角才达到45°,其余直线跟踪段,滚转角均在零附近。 图9 矩形航迹跟踪Fig.9 Rectangular course tracking 图10 五角星航迹跟踪Fig.10 Pentagram course tracking 由图11(a)和图11(b)可以看出,在进行圆形航迹跟踪时,传统的PD控制在初始误差较大时,易造成指令饱和,需重新规划航迹,否则难以将巡飞弹控制到给定航迹上。由图11(c)和图11(d)可知,PD控制收敛之后,存在较大的稳态误差,需引入前馈控制进行补偿。而L1制导律,在初始误差较大时,由于制导律中的正弦函数自带限幅作用,也可使航迹收敛,无需重新进行航迹规划,且跟踪的稳态误差小。 图11 PD控制与L1控制对比Fig.11 Comparison of PD control and L1 control 采用基于L1制导的巡飞弹航迹跟踪方法,将巡飞弹航迹跟踪问题分解为直线航迹跟踪和圆航迹跟踪,方法简单易行。由于制导律中引入正弦函数,可以防止航迹偏差较大时引起的超调。针对巡飞弹初始位置与理论航迹的相对位置关系,分别设计了前置角,使巡飞弹在任意方位均可快速收敛于理论航迹。通过仿真验证,所提出的航迹跟踪方法可对圆航迹和直线航迹有效跟踪。


2.2 直线航迹跟踪


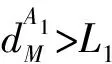


3 仿真验证



4 结论

