基于差分进化粒子群混合算法的多无人机协同区域搜索策略
赖幸君,唐 鑫,林 磊,王志胜,丛玉华
(1 国家无线电监测中心检测中心,北京 100041;2 南京航空航天大学自动化学院,江苏 南京 210016)
0 引言
无人机是一种可自主控制或通过无线电控制的无人驾驶航空器,与有人驾驶飞机相比,无人机具有成本低、体积小、机动性强、部署方便、在高危环境下无人员伤亡等优点[1],目前已被广泛应用于搜索、遥感、勘探等领域[2-6]。
目前针对未知区域的全区域覆盖和针对已知目标信息的搜索问题已有了大量研究,但对于未知环境的目标搜索问题研究相对较少。全区域覆盖方面,Muoz等[7]针对在杂乱的城市环境中执行区域覆盖任务时可能产生碰撞的问题,建立了考虑城市中障碍物的地图模型,并基于无冲突领航路径和领航-跟随者编队策略,计算所有无人机的路径。Chen等[8]针对异构无人机群在多个独立的区域进行大规模协作搜索任务时,计算复杂度高,难以求解的问题,提出基于蚁群算法求解近似最优的区域覆盖路径。Zhang等[9]针对多无人机在大范围区域中的覆盖问题,将该区域分解为可以被无人机相机完全覆盖的若干正三角形,并将需要覆盖的目标区域转换为由节点和边组成的连通图,并采用混合线性整数规划法来求解无人机的区域覆盖航路规划问题。
目标搜索问题的思想与区域覆盖相反,其主要目标为:用尽可能短的时间搜索到区域内的目标,减少多余搜索。Zhou等[10]为了在提高无人机搜索目标效率的同时,能躲避环境中的障碍物,提出了一种免疫遗传算法,并在返程阶段,设计了一种分而治之和确定性路径优化算法,解决无人机完成任务后的返程问题。Duan等[11]针对多无人机执行空中搜索任务的优化指标建立问题,利用贝叶斯公式构造和更新概率图,指导无人机的搜索。Yu等[12]针对灾害场景中的目标搜索问题,将无人机的飞行距离和航迹的风险加入考虑范围,使无人机能完成目标搜索任务的同时,减少无人机执行任务过程中发生意外的概率。
根据搜索任务需求提出的优化问题,设计合适的优化算法求解无人机的搜索路线是解决区域搜索问题的关键。由于待搜索环境往往有很大的不确定性,离线规划的算法在区域搜索问题中并不适用,需要无人机根据实时变化的环境调整搜索路线,这对算法的实时性要求较高。目前主流的算法主要有启发式算法(模拟退火法、遗传算法、蚁群算法、粒子群算法、狼群算法等)和人工智能优化算法(深度学习、强化学习等)[13]。启发式算法由于其在规定时间内必然可以给出可行解、且不依赖于模型的特点,被研究者们用于无人机实时决策问题上。Ghambari等[14]将几种典型的自然启发式算法应用于带约束的路径规划问题,为启发式算法在带约束问题中的应用提供了参考。Cho等[15]为搜索问题建立了混合整数线性规划模型,并开发了一种随机搜索启发式算法,减少计算时间的同时,保证了搜索方案的最优性。Zhu等[16]提出了一种分布式在线启发式策略,在其中融合了并行搜索和内螺旋搜索等几何特征,在多无人机协同区域覆盖问题中取得了较高的搜索效率。Han等[17]在考虑避障的区域覆盖路径规划问题中引入蚁群算法,在规划的路径长度和能耗方面取得了很好的性能。Kyriakakis等[18]针对无人机搜索和救援场景的动态优化问题,提出了一种多群框架,将多种群智能算法用于求解该问题,证明粒子群算法是众多算法中最有效的群智能算法。
综上分析,现有国内外研究虽然在多无人机协同区域搜索决策方法上有一定的研究,但仍存有以下问题有待研究解决:1)现有的区域搜索方法考虑的因素不够全面,当综合考虑多项优化指标后,传统的群智能优化算法求解区域搜索问题易陷入局部最优,导致搜索性能不佳;2)传统群智能优化算法在求解复杂多目标优化问题时寻优时间更长,实时性较差。
针对以上问题,开展了以下研究:首先为了提高多无人机协同区域搜索综合性能,将区域覆盖率、区域不确定度、目标发现概率加入优化目标,作为衡量区域搜索性能的指标;其次提出一种基于差分进化粒子群混合算法的无人机区域搜索策略,提高搜索性能和寻优效率;最后通过充分的仿真实验,验证所提算法在多无人机协同区域搜索问题中的性能。
1 问题描述
文中主要针对区域内目标数量NT未知,区域内目标分布情况未知的场景下,NU架无人机飞入待搜索区域,利用自身携带的传感器对区域进行自主搜索,根据无人机获得的区域地图信息,在线自主决策,在规定的任务时间内,尽可能多地发现未知目标,并覆盖尽可能多的未知区域,从而掌握区域内的信息。任务的示意图如图1所示。
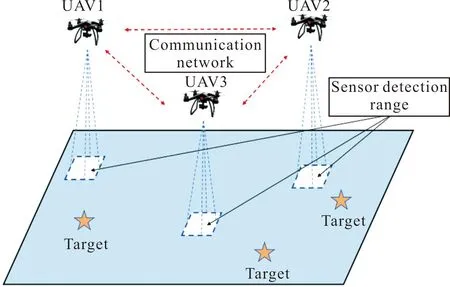
图1 多无人机区域搜索任务示意图Fig.1 Multi-UAV area search mission diagram
1.1 搜索环境模型
在多无人机区域搜索场景中,NU架无人机对区域内的NT个目标进行搜索和位置确认。无人机用Ai(1≤i≤NU)表示,待搜索目标用Tj(1≤j≤NT)表示。
将待搜索区域Ω离散成网格图[19-21],如图2所示。网格图由Lx×Ly个网格构成,每个网格的长和宽分别为Δx和Δy。根据网格图建立二维坐标系,第m行第n列的网格中心的坐标为(m,n),其中1≤m≤Lx,1≤n≤Ly。
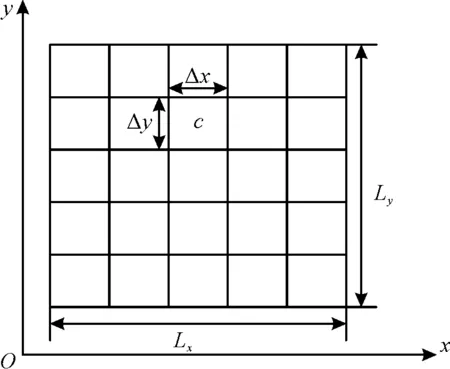
图2 网格化后的待搜索环境Fig.2 Environment to be searched after gridding
假设每个网格中最多存在一个目标,那么网格中的目标存在情况可表示为:
sc={(xc,yc,ξc)|c∈Ω}
(1)
式中:xc和yc分别为网格c的x轴坐标和y轴坐标;ξc为网格c处的目标存在状态。ξc可表示为:
(2)
文中采用旋翼无人机执行区域搜索任务。由于传感器的检测性能受无人机飞行高度影响,为了便于无人机判断,将无人机设为固定高度,从而使无人机机载传感器的探测范围固定。无人机的运动学模型简化为:
(3)
式中:xi(t),yi(t)为无人机的空间坐标;Vi(t)为无人机i的飞行速度;φi(t)为无人机i飞行方向与x轴正方向的夹角;ωi(t)为无人机转弯时的角速度。
无人机基于式(3)所示的运动模型在待搜索区域中运动,航向角φi可为[-180°,180°]区间内的任意值,速度Vi(t)需满足无人机最大飞行速度约束,即Vi(t)≤Vmax。无人机在空中的飞行时间需满足无人机最大续航时间,即t≤tmax。
1.2 区域信息地图
为准确反映无人机对区域的搜索情况,下面建立无人机的目标存在概率图模型、区域不确定度地图模型、区域覆盖图模型。
1.2.1 目标存在概率图
根据任务环境的地形与目标类型,建立目标存在概率图。随着无人机搜索的进行,无人机对区域内的探测结果会影响后续对目标位置的判断,每架无人机建立目标存在概率地图[22]可表示为:
Mi,prob(k)={pi,c(k)|c∈Ω}
(4)
式中pi,c(k)为无人机i的概率地图中网格c处的目标存在概率。
根据贝叶斯公式[23],更新k时刻在无人机视场范围内的网格的目标存在概率pi,c(k)为:

(5)
式中:pd为无人机的探测概率;pf为无人机的虚警概率;Φi,k为无人机的传感器探测范围,若k时刻无人机i在网格c中发现目标,无人机的探测结果表示为Wi,c(k)=1,反之,探测结果表示为Wi,c(k)=0。
1.2.2 区域不确定度地图
为了将无人机对网格的信息认知程度量化,以反映无人机是否了解区域中的目标存在情况,引入区域不确定度ηi,c(k),建立区域不确定度地图[24]:
(6)
式中Kη>0,为常数。根据式(6)与式(7)可以得出区域不确定度ηi,c(k)与目标存在概率pi,c(k)的关系。
1.2.3 区域覆盖地图
为了准确表示待搜索区域中被无人机搜索过的区域面积,文中用区域覆盖状态Cc(k)表示无人机对网格c的覆盖情况:
(7)
根据整个区域网格覆盖状态,可以将无人机对环境的区域覆盖率[25]C(k)表示为:
(8)
式中Gall为环境网格地图中的网格总数。
2 多无人机协同区域搜索策略
2.1 无人机区域搜索滚动时域优化模型
在无人机区域搜索问题中,由于环境的未知与多变性,离线解算的结果无法适应动态变化的环境,因此,文中借鉴模型预测控制中的滚动时域优化思想[26-30],建立小规模优化目标,无人机只需求解预测的时间窗范围内的最优动作,降低计算的难度。无人机的滚动时域优化模型可表示为:

(9)
式中:U*(k)为决策的控制输入序列;U(k)={u(k),u(k+1),…,u(k+tw)}为无人机在动态时间窗内的输入决策序列;tw为动态时间窗长度;X(k)为k时刻的状态输入,包括k时刻的区域覆盖图、目标存在概率图、区域不确定度地图以及所有无人机的位置信息、能量消耗情况;Jc,Jp,Ju分别为区域覆盖率目标函数、目标发现概率目标函数、区域不确定度目标函数;Je为无人机能量消耗代价函数,用于减少无人机在搜索过程中的能量消耗;λc,λp,λu,λe分别为四种优化目标对应的权重系数。
2.2 基于差分进化粒子群混合算法的无人机区域搜索策略
为了防止无人机的搜索路线过早陷入局部最优,对差分进化算法(DE)和粒子群优化算法(PSO)取长补短,提出基于差分进化粒子群混合算法(PSODE)的区域搜索策略,求解所提出的多目标优化问题。PSODE算法的寻优过程如图3所示。
基于PSODE算法规划无人机搜索路线的总体步骤如下:
步骤1:分别为DE算法和PSO算法产生n个初始随机解Ui,de(k)、Ui,pso(k),i=1,2,…,n(即为无人机的控制决策输入)。
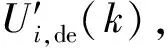
(10)
式中:Ui,pso(k)为粒子群算法解集中第i个解(简称为粒子i);Vi为粒子i的更新速度;Gbest(k)为k时刻Ui,pso(k)中的全局最优解;c1,c2分别为个体学习因子和群体学习因子;r1,r2为区间[0,1]内的随机数;w为惯性权重,表示当前迭代轮次受上一轮迭代速度的影响程度。根据Gbest(k)计算出粒子群算法中的最优适应度函数fpso。
步骤4:比较fde,fpso,取其最大值作为全局最优适应度fpg,计算DE算法与PSO算法的选择概率pselde,pselpso,其中DE算法的选择概率计算公式为:
(11)
其中,λ1和λ2的计算方式分别为:
(12)
(13)
相对应的,PSO算法的选择概率为:
pselpso=1-pselde
(14)
步骤5:产生0~1之间的随机数Nrand,若Nrand
步骤6:若未达到设定的最大迭代次数,则按步骤5的方式不断更新Ui,de(k);Ui,pso(k);否则,比较fde与fpso,若fde>fpso,则选用Ui,de(k)作为无人机的控制输入;否则,将Ui,pso(k)作为无人机的控制输入。
为了让算法能在收敛速度和寻优精度取得均衡,文中对算法中的PSO算法和DE算法均采用自适应参数调整的策略。
在PSO算法中,种群的更新速度和精度主要受惯性权重w影响,文中对w采用线性递减策略,w的更新公式为:
(15)
式中:wmax为惯性权重的最大值;wmin分别为惯性权重的最小值;Nmaxit为最大迭代次数。
在DE算法中,变异因子F是影响其种群更新的关键参数。在进化早期,种群应扩大搜索范围寻找最优解,此时F的值应较大,随着进化过程的进行,F的值应逐渐变小,由全局搜索转变为以局部搜索为主,精准寻优。因此,DE算法的变异因子F采用如下的自适应调整方式:
(16)
式中,Fmax与Fmin分别为最大变异因子和最小变异因子。
3 仿真分析
为验证基于PSODE算法的无人机区域搜索策略的有效性,首先,在相同环境下,对比基于PSODE算法的无人机区域搜索策略与单一的PSO算法、DE算法的性能差异;其次,进行多次实验,对比三种算法的性能指标平均值与方差,验证算法的稳定性;最后分析迭代次数对算法性能的影响,验证提出的PSODE算法在实时性方面的性能。
3.1 仿真参数设置
设置环境未知的待搜索区域大小为30 km×30 km,将待搜索区域进行网格化处理,将区域划分为30×30的网格图,执行任务的无人机数量为3,无人机的初始位置分别为(2 km,2 km)、(28 km,2 km)、(2 km,28 km),无人机携带的传感器探测概率pd为0.8,虚警概率pf为0.2,认为网格中存在目标的概率阈值设置为0.9;设置执行未知区域搜索任务的时间为30 min,无人机的能耗模型参考文献[30]。优化算法的参数设置方面,PSO算法的初始惯性系数wstart为0.8,末尾惯性系数wend为0.2,更新速度Vd范围限制设置为[-1,1],个体学习因子c1与群体学习因子c2均为0.25。DE算法的初始变异因子Fmax为0.65,末尾变异因子Fmin为0.3,交叉概率CR为0.9;PSODE算法的参数与PSO算法和DE算法的参数均相同。
3.2 算法计算结果分析
分别采用DE算法、PSO算法和PSODE算法求解多无人机协同区域搜索问题,三种算法的搜索结果图如图4~图6所示,DE算法在任务过程中会产生较多的重复搜索,导致搜索效率不高,有大片区域未被搜索。基于PSO算法的无人机区域搜索策略在搜索后期,无人机会存在重复搜索的问题。PSODE算法重复搜索的频率比PSO算法和DE算法更低,搜索结束时对区域的覆盖率更高,可将区域不确定度降至更低。
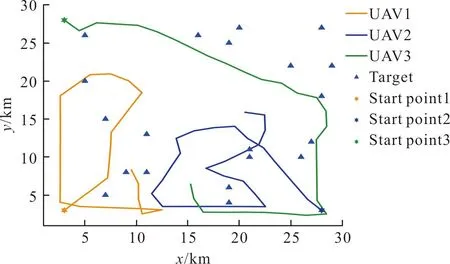
图4 基于DE算法的搜索结果图Fig.4 Search result graph based on DE algorithm

图5 基于PSO算法的搜索结果图Fig.5 Search result graph based on PSO algorithm
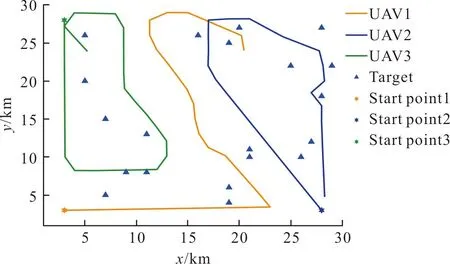
图6 基于PSODE算法的搜索结果图Fig.6 Search result graph based on PSODE algorithm
无人机在搜索结束时的区域覆盖率、区域不确定度与消耗的总能量对比如表1所示。文中提出的PSODE算法可达到97.26%的区域覆盖率,分别比PSO算法和DE算法高1.59%、10.04%;搜索完成后的区域不确定度方面,提出的PSODE算法分别比另外两种算法低2.46%、9.87%,对区域的信息掌握程度更高;用于转弯消耗的能量分别比PSO算法和DE算法少57.74%、61.25%;发现目标数方面,三种算法几乎相同。综合四项性能指标可以看出,基于PSODE算法的区域搜索策略在相同条件下,具备更好的搜索性能。

表1 三种算法的区域搜索结果性能比较Table 1 Performance comparison of area search results for three algorithms
3.3 迭代次数对算法性能的影响分析
由于无人机需要在线决策搜索路线,因此对算法的实时性要求较高,本节对不同迭代次数下三种算法的区域搜索性能进行量化分析,验证迭代次数对算法性能的影响。分别设置算法的迭代次数为20,50,100,在相同环境中进行次数为20仿真实验,对比结果如图7和表2所示。
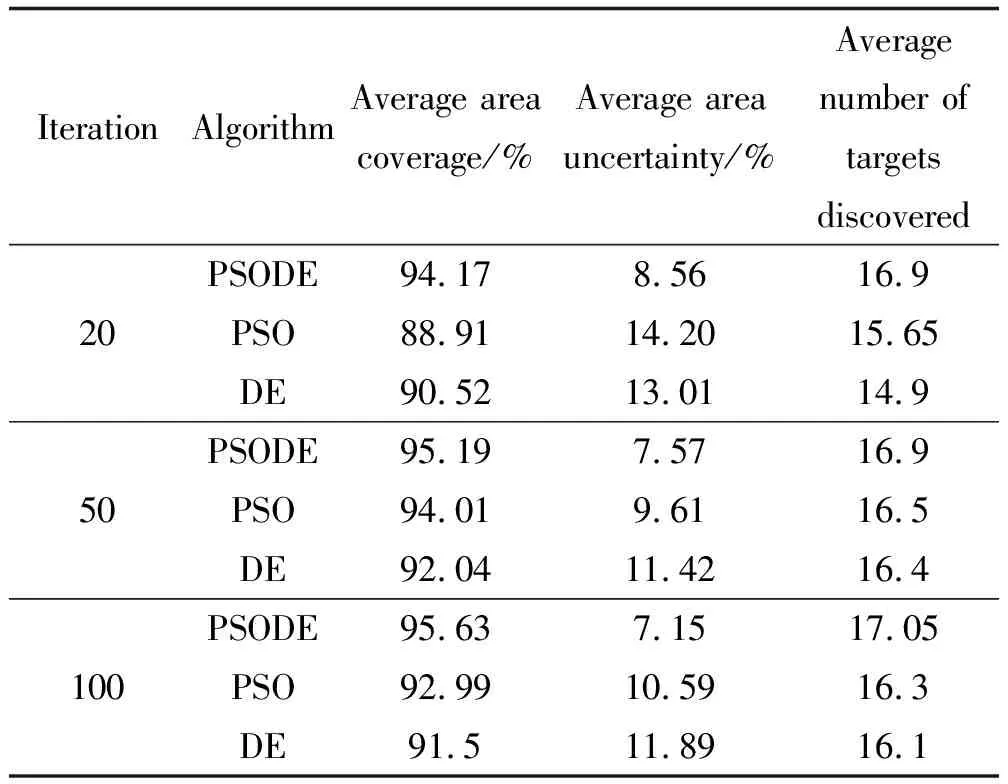
表2 不同迭代次数下三种算法的性能指标情况Table 2 Performance indexes of the three algorithms with different number of iterations

图7 不同迭代次数下三种算法的性能指标情况Fig.7 Performance metrics of the three algorithms with different iterations
由图7可知,相同迭代次数下,文中提出的基于PSODE算法的区域搜索策略各项性能指标的方差比其他两种未改进的算法小,在区域搜索过程中表现出的性能更稳定。
表2为仿真实验中算法不同迭代次数的平均性能指标,由数据可以看出,随着迭代次数的提升,三种算法的性能指标均有不同程度的提高,基于PSODE算法的区域搜索策略在迭代次数20时,平均区域覆盖率就已经达到94.17%,比另外两种算法高5.26%,3.65%,区域不确定度降低至8.56%,比其他两种算法低5.64%、4.45%,平均发现目标数为16.9,分别比其他两种算法多1.25、2,且PSODE算法在迭代次数20时,便已获得比其他两种算法100次迭代时更优的性能,由此可见基于PSODE算法的区域搜索策略具备更好的实时性。
3.4 目标函数权重系数影响分析
在提出的滚动时域优化模型中,λc,λp、λu与λe分别表示无人机执行区域搜索任务时对区域的覆盖率、发现目标概率、区域不确定度和无人机能量消耗四个方面的权重,为了验证不同的权重对无人机区域搜索策略的影响,将权重系数按表3中的组合分别进行仿真分析。

表3 无人机区域搜索优化目标权重系数组合Table 3 Combination of target weight coefficients for UAV area search optimization
三种权重组合的航迹图如图8所示。在待搜索区域中,红色区域和绿色区域为无人机开始搜索前,根据已知的地形推测出的部分已知目标存在概率的区域,其中红色区域表示目标存在概率为0.8,绿色区域表示目标存在概率为0.2,其他区域的信息完全未知,目标存在概率为0.5。三种权重组合分别对应了不同的任务需求。
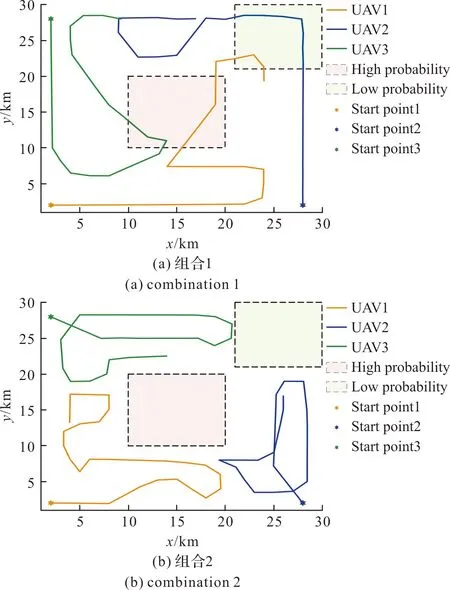
图8 不同权重系数下无人机区域搜索航迹Fig.8 UAV regional search trajectory with different weighting factors
搜索性能的指标变化曲线如图9所示。在区域覆盖率方面,组合1权重下的区域搜索策略,获得的区域覆盖率最高,为95.56%,分别比组合2和组合3高20.56%、18.00%,;在区域不确定度方面,组合2的不确定度下降速度更快,任务完成时,组合2与组合1的区域不确定度分别为6.15%、6.21%,分别比组合3低11.64%、11.58%;无人机搜索区域的目标存在概率方面,权重组合3的搜索路线会优先搜索目标存在概率高的区域,搜索过的区域目标存在概率总和曲线上升速度比组合1和组合2快。在实际应用时,可选择不同的权重组合以适应不同的任务需求。

图9 不同权重系数无人机区域搜索性能指标变化曲线Fig.9 Change curve of UAV area search performance index under different weighting factors
4 结论
文中针对未知环境下的无人机区域搜索问题,提出基于差分进化粒子群混合算法的无人机区域搜索策略,解决了现有的区域搜索方法总体性能不佳、实时性差的问题,从区域覆盖率、目标发现概率、区域不确定度和能量消耗4个方面提升了无人机区域搜索性能,从仿真结果可以看出,所设计的基于差分进化粒子群混合算法的无人机区域搜索策略可获得比基于粒子群算法、差分进化算法的区域搜索策略更优的搜索性能,并具备较好的实时性和稳定性。然而,文中提出的区域搜索策略未考虑无人机在环境中可能遇到意外事件损毁的情况,未来计划将无人机损毁情况加入考虑范围,使区域搜索策略可适应更为复杂的环境。

