温度及预紧载荷对氧化石墨烯无石棉垫片蠕变松弛和泄漏率的影响

张静全，李遇贤，郭子玉，张 杰

(昆明理工大学机电工程学院，云南 昆明650500)

1 前 言

螺栓法兰系统由于易于拆卸，在石油、化工、核能、航天航空等行业得到广泛应用[1]。螺栓法兰系统的密封失效很少是由螺栓和法兰强度不足引起的，大部分都是由垫片泄漏引起的，所以垫片在螺栓法兰系统中起着至关重要的作用[2]。垫片是静密封中确保机器设备和传送系统安全、无泄漏工作的一种基础零部件，是汽车、航空航天、化工、石油和船舶等工业生产中避免重大安全事故的重要保障[3]。垫片的蠕变松弛性能是影响螺栓法兰系统密封性能的重要性能之一，因为它会导致垫片的应力松弛，从而引起法兰接触面之间存在间隙，使得螺栓法兰系统密封性能下降，甚至导致介质发生界面泄漏[4]。而高温和预紧载荷是影响蠕变松弛和泄漏的主要因素。关于垫片的蠕变松弛性能及泄漏率，国内外学者进行了大量的研究工作。Sato等[2]采用有限元计算和实验研究了高温下聚四氟乙烯混合垫片螺栓连接管法兰的力学特性，利用有限元计算得到的接触垫片应力分布以及垫片应力与泄漏率之间的关系，预测了螺栓管法兰连接的密封性能。徐浩等[5]研究高温下不含垫片的螺栓连接装置的蠕变松弛机制，结果表明，高温下螺栓预紧力越大，随着时间的推移损失的预紧力越大，但残余预紧力也越大。Wasmi等[6]提出用四元模型预测垫片连接系统在蠕变松弛过程中的残余应力，研究选用的垫片材料为丁苯橡胶；Housari等[7]在四元模型的基础上，预测螺栓连接中垫片的蠕变下应力下降，并考虑垫片行为、螺栓刚度和接头刚度，选用的垫片材料同样为丁苯橡胶；Williams等[8]通过一组实验确定Burgers模型的常数，将模型用来表征和分析垫片螺栓接头的初始和扭转载荷松弛响应，选用的垫片材料为添加25%玻璃纤维增强的聚四氟乙烯。Grine等[9]分析了不同温度下泄漏率、垫片位移和介质内压之间的关系，提出了高温下垫片泄漏率的预测方法。近年来氧化石墨烯(graphene oxide，GO)作为新型纳米增强填料在复合材料中的显著增强作用引发极大关注。GO作为一种新型纳米增强填料，以较低的加载量就可显著增强聚合物复合材料的力学性能[10]。Wang等[11]使用GO来增强聚乙烯醇，结果表明，当GO的添加量从0.5%增加到4%(质量分数)时，材料表现出增强效果。Berki等[12]等采用GO对天然橡胶胶乳进行改性，GO和十六烷基三甲基溴化铵之间的π-阳离子相互作用可以调整界面相，从而调整天然橡胶纳米复合材料的相关性能。关于GO在复合材料的应用研究表明，GO少量的添加就能大幅度提升材料性能[13]。

以上研究表明，有限元技术和Burgers模型是研究螺栓法兰系统蠕变松弛和泄漏率的有效手段，但是目前相关的研究常把重心放在非金属垫片及橡胶垫片等的蠕变松弛及泄漏率，很少针对氧化石墨烯无石棉垫片。本文使用Burgers模型来研究氧化石墨烯无石棉垫片在不同温度和不同预紧载荷下的蠕变松弛，并通过实验得出氧化石墨烯无石棉垫片的蠕变松弛实验值，对比分析Burgers模型的准确性；其次提出随时间变化的垫片泄漏率计算方法，并讨论氧化石墨烯无石棉垫片在蠕变松弛过程中泄漏率随时间变化规律。

2 蠕变松弛理论模型

解决复合材料的非线性粘弹性问题，最重要的是建立与材料对时间的响应一致或接近的粘弹性模型，并通过模型建立对应的本构方程，研究复合材料由于粘弹性特点所发生的蠕变松弛现象。考虑到氧化石墨烯无石棉垫片作为复合材料，其蠕变松弛过程具有非线性粘弹性材料的特点，将Maxwell模型和Kelvin-Voigt模型串联起来组成粘弹性复合材料蠕变松弛模型，也叫Burgers模型[8]，如图1所示。Burgers模型由一个刚度为E1的理想弹簧1、粘度系数为η1的理想粘壶1串联，再加上刚度为E2的理想弹簧2与粘度系数为η2的理想粘壶2并联。

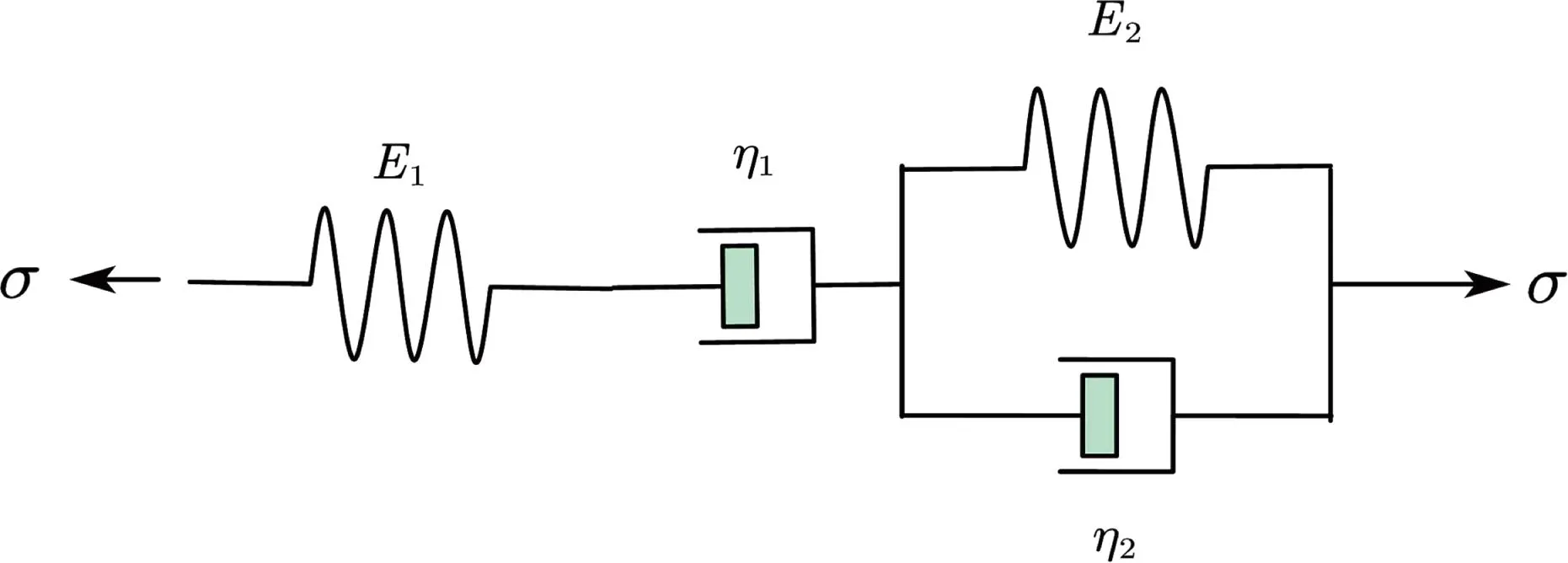
图1 氧化石墨烯无石棉垫片的Burgers模型Fig.1 Burgers model of graphene oxide non-asbestos gaskets

当螺栓法兰垫片系统开始工作前，首先将螺母拧紧，如图2所示，此时，垫片受到压缩预载荷将发生压缩变形，垫片的变形完全由弹簧1决定，处于弹性形变阶段；弹簧1的变形产生反弹力作用，对于粘壶2和弹簧2并联的部分来说，由于粘壶粘滞力的存在，使得变形缓慢，应变不能迅速发生，但随着时间的增加，恒定的应力迫使粘壶2进行活塞移动，随着粘壶2的逐渐形变弹簧2也慢慢发生形变，类似于高分子材料中分子链段运动必须克服内摩擦阻力而逐渐发展的蠕变过程的高弹形变阶段；随着垫片受到压缩后其厚度变薄，螺栓松弛，垫片所受压缩载荷也逐渐下降，因为粘壶1反应滞后，弹簧1以及粘壶2和弹簧2并联的部分发生应变而对粘壶1活塞的推动作用致使其发生形变，也就是蠕变过程的黏流形变阶段，导致应力松弛。由此可见，在Burgers模型中，当垫片受到压缩时，各元件表现出不同的应力和应变行为。粘壶2和弹簧2并联的部分表征了短期的蠕变松弛行为；粘壶1表征了随着时间的增加应力缓慢松弛行为，长时间内的缓慢松弛特性由垫片材料决定；弹簧1表征了垫片的弹性行为。

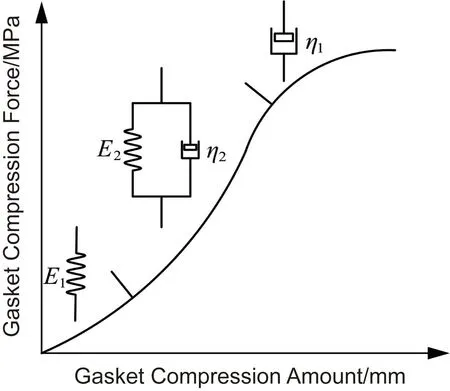
图2 氧化石墨烯无石棉垫片承受压缩力和压缩变形曲线Fig.2 The compression force and compression deformation curve of graphene oxide non-asbestos gasket

Burgers模型也可以看成是弹簧、粘壶和粘弹性元件3部分串联而成，设弹簧1的应变为ε1，粘壶1的应变为ε2，粘壶2和弹簧2并联的粘弹性部分的应变为ε3。由图1可以得到如下关系：

(1)

(2)

(3)

令总应变ε=ε1+ε2+ε3，则可以得到总应变与时间t的关系为：

(4)

式中，σ0为初始压缩应力。式(4)可以预测氧化石墨烯无石棉垫片的应变与时间的关系，上式也可以写成：

(5)

图3为氧化石墨烯无石棉垫片的压缩回弹曲线，由图可知施加压缩载荷并卸载后，垫片应力和应变之间的关系均呈现出非线性的特征，加载路线和卸载路线不重合，在图形上表现出滞回曲线的特征，即存在残余变形，说明垫片在卸载后均不能完全还原，而是存在一定的残余压缩量和回弹量，这也证明了垫片具有一定的粘弹性的特点。压缩回弹曲线中压缩曲线下的面积表示压缩垫片所做的功将以弹性应变能储存在垫片中，面积越大说明弹性补偿的能力越大，回弹曲线以下的面积则表示在卸载时释放出来的弹性应变能。显然，加载应力越大，则储存的弹性应变能越大，所以在垫片可承受的范围内，适当增加压紧力能提高螺栓密封可靠性。应力与应变之间的变化规律符合Burgers模型。式(5)可以改写为：

(6)

图3 氧化石墨烯无石棉垫片压缩回弹曲线Fig.3 Compression rebound curve of graphene oxide non-asbestos gasket

式(6)将应力松弛量σ(t)表达成时间的函数，ε0为螺栓预载荷下垫片的初始应变，可以进一步得到垫片的刚度与时间的关系表达式为：

(7)

垫片的刚度是比较复杂的，垫片在螺母预紧后，经历粘弹性蠕变和松弛，蠕变引起垫片厚度变化，从而引起应力松弛，垫片厚度对性能具有非线性影响，所以粘弹性行为导致的刚度损失是垫片变薄的原因，进而导致接头承受的载荷松弛。

而对于式(7)中的参数E1，E2，η1，η2而言，可以按以下方法进行求取，当t=0时：

(8)

当t>0时，式(5)中的指数项可以忽略不计，在t1和t2时刻，应变与垫片应力之间的关系为：

(9)

再取时间比较短的时刻t3：

(10)

联立式(8)～式(10)，即可得E1，E2和η1，η2。

3 实验材料与方法

本文选用的垫片为氧化石墨烯无石棉垫片，该垫片是一种低成本的垫片材料，在低压应力作用下就能提供良好的密封性能，并且也容易适应不平整的法兰面。采取抄取法制备氧化石墨烯无石棉垫片试样，通过实验验证蠕变松弛模型的可行性。

3.1 原料、试剂及仪器设备

所用原料有：无石棉纤维(纸浆纤维、芳纶纤维、矿物棉纤维、QY棉纤维)，胶乳粘合剂(丁腈胶乳、丁苯胶乳)，硫化剂(硫、氧化锌、二硫化四甲基秋兰姆)，填料(高岭土、滑石粉、云母、GO)，硫酸铝，消泡剂，絮凝剂。所用仪器包括：PL28-00型标准疏解机、PL12-A型水力碎浆机、PL6-C型纸样抄取器、PL8-D型电热压榨机、DZF-6090真空干燥箱、XLB-Q4004002平板硫化机、HLYL-4系列密封垫片应力松弛试验机。

3.2 实验配方

试样制备配方为：芳纶纤维，6 g；纸浆纤维，15 g；矿物棉纤维，15 g；QY棉纤维，10 g；高岭土，20 g；滑石粉，8 g；云母，4.5 g；GO，0.2 g；丁腈胶乳，8 g；丁苯胶乳，3 g；硫酸铝，9 g；氧化锌，0.6 g；二硫化四甲基秋兰姆，0.6 g；S，0.3 g；消泡剂，0.2 g；絮凝剂，0.1 g。

3.3 蠕变松弛实验

试样的尺寸为Φ75 mm×Φ55 mm×2 mm，实验温度为25，50，100，150和200 ℃，垫片预紧载荷为30，40和50 MPa，实验时间为24 h。通过蠕变松弛试验机测试氧化石墨烯无石棉垫片在5种温度及3种预紧载荷下的蠕变松弛。

4 结果与讨论

4.1 蠕变松弛模型实验验证

图4a为垫片预紧载荷为30 MPa时不同温度下垫片的应力，可知在使用时间约前700 min时，垫片应力下降速率随着温度的升高而降低，主要因为垫片在初始阶段温度越高膨胀越剧烈；在使用时间约700 min后，垫片应力下降速率随着温度的升高而升高，并且温度为200 ℃时垫片的应力松弛量达到最大值。图4b和4c与图4a有相似的变化规律。比较图4a～4c可知，垫片应力的松弛量随着预紧载荷的增加而增加；随着使用时间的增加，垫片的应力松弛变得更加平缓。使用时间达24 h时，垫片预紧载荷分别为30，40和50 MPa时，对应的的应力松弛量为3.3653，3.4509和4.4172 MPa。

图4 不同温度及预紧载荷下垫片应力随时间变化：(a)30 MPa，(b)40 MPa，(c)50 MPa Fig.4 Variations of gasket stress with time under different temperatures and preloads：(a) 30 MPa，(b) 40 MPa，(c) 50 MPa

使用Burgers蠕变松弛模型来预测氧化石墨烯无石棉垫片的蠕变松弛性能，需要将实验数据代入式(8)～式(10)计算出蠕变松弛模型中4个参数：E1，E2，η1和η2，表1列出不同预紧载荷及温度下蠕变松弛模型的4个参数。再将这4个参数代入式(6)，就可以得到垫片应力和时间的函数关系式。以预紧载荷30 MPa和温度25 ℃为例，垫片应力和时间的函数关系式如式(11)所示：

(11)

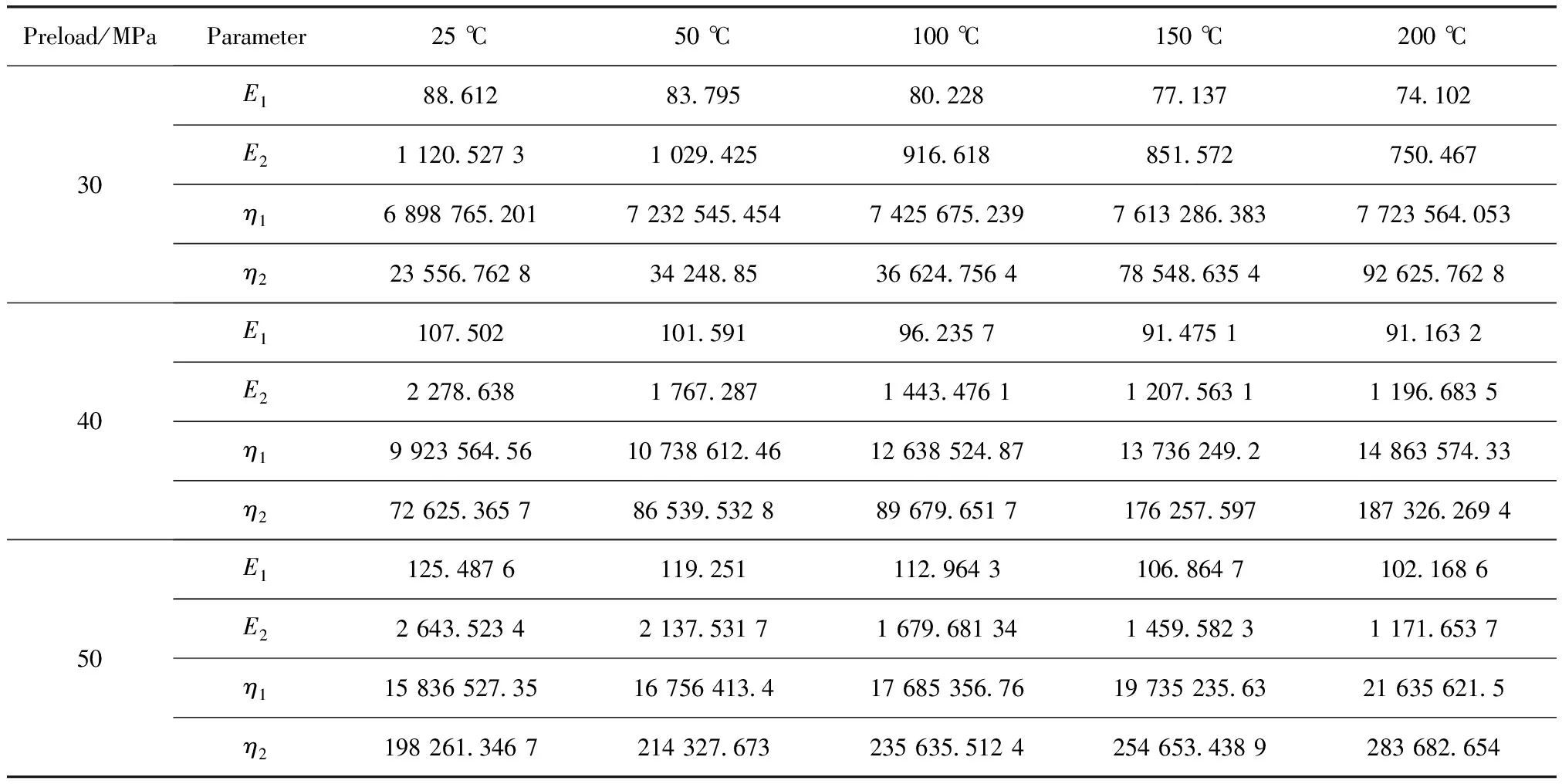
表1 不同预紧载荷及温度下蠕变松弛模型的参数

图5为5种温度及3种预紧载荷下垫片蠕变松弛实验结果和模型计算结果的对比，可以看出，实验数据与模型计算结果吻合度很好，之间的最大误差为4.4728%，这可能是由于垫片机械性能的正常变化或者实验的误差造成的。因此，该蠕变松弛模型可以用于预测氧化石墨烯无石棉垫片的蠕变松弛行为。

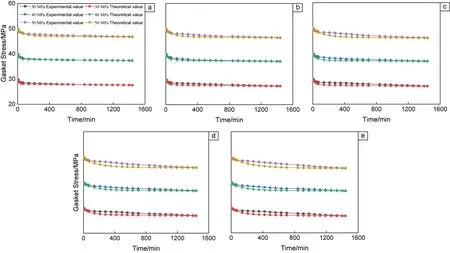
图5 不同温度及预紧载荷下垫片蠕变松弛的实验结果和模型计算结果：(a)25 ℃，(b)50 ℃，(c)100 ℃，(d)150 ℃，(e)200 ℃Fig.5 Experimental and theoretical values of gasket creep relaxation under different temperatures and preloads：(a) 25 ℃，(b) 50 ℃，(c) 100 ℃，(d) 150 ℃，(e) 200 ℃

4.2 垫片泄漏率计算

为了表征氧化石墨烯无石棉垫片密封性能，美国压力容器研究委员会(PVRC)工作组提出了密封性的概念。

密封性与泄漏率成反比，PVRC将气密性分为5个等级，并定义了相对于每个气密性等级的质量泄漏率，用于表征氧化石墨烯无石棉垫片的气密性，如表2所示。

表2 PVRC密封等级

Bausman等[14]给出了实际泄漏率和最终操作气密性参数之间的关系，如式(12)所示：

L=[(145P/14.7)×(1/Tf)]2/150

(12)

式中，L为实际泄漏率，mg·s-1·mm-1；Tf是最终操作气密性参数，无量纲；P是内压，MPa。Tf与垫片参数和垫片应力有关，计算公式如下：

Tf=(Sf/Gs)(1/kf)

(13)

Sf=r[ηSg-P(Ai/Ag)]

(14)

kf=log(ηSg/Gs)/logTp

(15)

Tp=(ηSg/Gb)(1/a)

(16)

式中，Gb、a和Gs为垫片参数，Gb和Gs的单位为MPa，a的单位为无量纲；Sg为垫片初始应力，MPa；Sf为工作垫片应力，MPa；r为应力保持系数，介于0.1和1.0之间，无单位；η是装配效率，无单位；P为内压，MPa；Ai为垫片内部受压面积，mm2；Ag为垫片的接触面积，mm2；kf是垫片实验中卸载曲线的斜率，无量纲；Tp为气密性参数，无量纲。

氧化石墨烯无石棉垫片在不同温度下长期使用过程中，垫片应力也会随着使用时间变化而变化，因此，垫片的泄漏率也与时间有关，为了获得垫片在高温下使用时泄漏率的计算方法，有必要建立泄漏率与使用时间之间的关系。式(11)～式(16)建立了泄漏率、垫片参数和垫片应力之间的关系，但这种关系与使用时间无关。通过分析，可以用不同温度下长期使用期间随时间变化的垫片应力代替工作垫片应力Sf，以考虑时间因素。在此基础上，参考文献[15]推导得出Sg的数值，并再次使用最小安装垫片应力Sm代替垫片初始应力Sg，得出泄漏率、垫片参数、垫片应力与使用时间之间的关系，从而得到在不同温度下长期使用时垫片泄漏率的计算方法，计算公式如式(17)所示：

(17)

根据上述确定的泄漏率、垫片参数、垫片应力与使用时间之间的关系，如果已知氧化石墨烯无石棉垫片在不同温度下长期使用期间随时间变化的垫片应力，则可以计算出垫片随着时间变化的垫片泄漏率。将实验得到的不同温度及不同预紧载荷下随时间变化的垫片应力Sf代入方程(17)中，可以得到氧化石墨烯无石棉垫片在不同温度及不同预紧载荷下随时间变化的泄漏率，从而可以得出垫片在不同温度及不同预紧载荷下的密封性，如图6所示。从图6可以看出，在相同的预紧载荷和温度下，垫片的泄漏率随使用时间的增加而增加；预紧载荷为30 MPa和使用时间在约前700 min时，泄漏率增加速率随着温度的升高而下降，随着时间继续增加，泄漏率增加速率随着温度的升高而升高，并且温度为200 ℃时垫片的泄漏率达到最大值，为1.31×10-3mg·s-1·mm-1；预紧载荷为40 MPa和使用时间在约前600 min时，泄漏率升高速率随着温度的升高而下降，随着时间继续增加，泄漏率增加速率随着温度的升高而升高，温度为200 ℃时垫片的泄漏率达到最大值，为8.27×10-4mg·s-1·mm-1；预紧载荷为50 MPa和使用时间在约前500 min时，泄漏率增加速率随着温度的升高而下降，随着时间继续增加，泄漏率增加速率随着温度的升高而升高，温度为200 ℃时垫片的泄漏率达到最大值，为6.01×10-4mg·s-1·mm-1；在相同的温度和使用时间下，氧化石墨烯无石棉垫片计算的泄漏率随着预紧载荷的增加而降低，且泄漏率均小于密封等级T2的泄漏率(2×10-3mg·s-1·mm-1)。

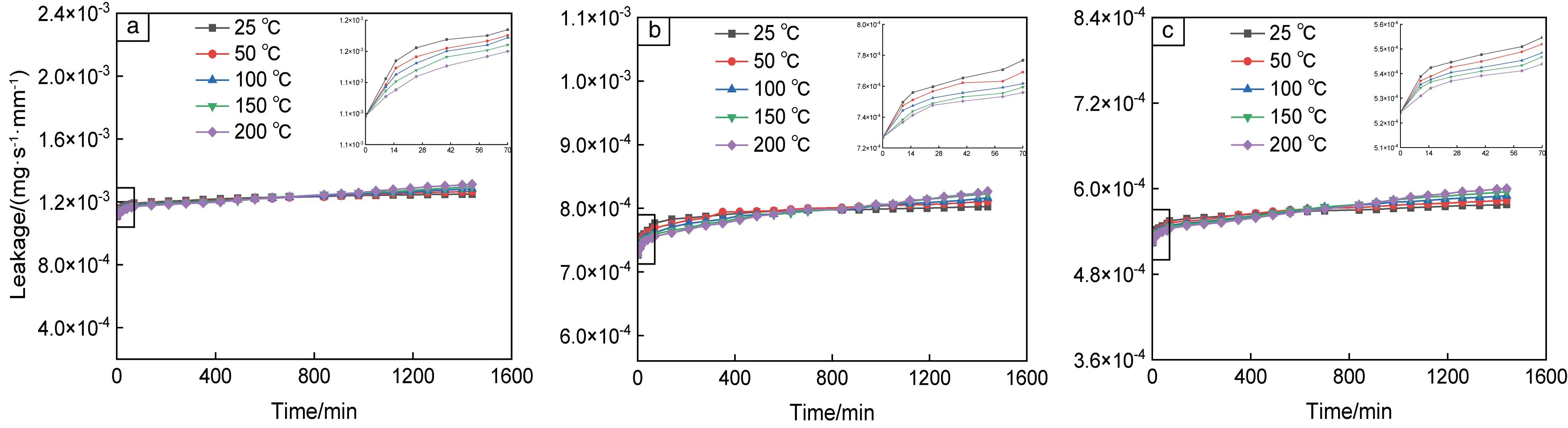
图6 不同温度及预紧载荷下垫片泄漏率随时间变化：(a)30 MPa，(b)40 MPa，(c)50 MPa Fig.6 Variations of gasket leakage rate with time under different temperatures and preloads：(a)30 MPa，(b) 40 MPa，(c) 50 MPa

5 结 论

(1)对氧化石墨烯无石棉垫片进行不同温度和不同预紧载荷下的蠕变松弛实验。垫片应力的松弛量随着预紧载荷的增加而增加；随着使用时间的增加，垫片的应力松弛变得更加平缓；在垫片预紧载荷相同的情况下，温度越高垫片应力下降得越明显。

(2)通过Burgers模型计算出垫片在不同温度和不同预紧载荷下的垫片应力值，并与实验值进行对比分析。结果表明，Burgers模型预测值与实验值吻合度很好，最大误差为4.4728%，因此该蠕变松弛模型可以用于预测氧化石墨烯无石棉垫片的蠕变松弛行为，并且通过Burgers模型预测值可以预测垫片的泄漏率。

(3)提出将氧化石墨烯无石棉垫片在不同温度及不同预紧载荷下长期使用时的垫片应力代替最终工作垫片应力，并提出氧化石墨烯无石棉垫片在不同温度和不同预紧载荷下长期使用时的泄漏率计算方法，并计算出垫片随时间变化的泄漏率变化规律。当温度相同时，垫片的泄漏率随预紧载荷的增加而减小；当预紧载荷和温度相同时，垫片的泄漏率随使用时间的增加而增加；当预紧载荷相同时，垫片的泄漏率随温度的增加而增加，且泄漏率均小于密封等级T2的泄漏率(2×10-3mg·s-1·mm-1)。