迎风格式在接触间断的数值耗散及其诱导误差

韩 芳,魏雁昕,刘 君

(大连理工大学 航空航天学院, 辽宁 大连 116024)

在计算流体力学(computational fluid dynamics, CFD)中,数值耗散主要来自空间离散格式离散对流项和时间离散格式离散时间项所产生的截断误差,其大小与格式的计算精度及稳定性息息相关。因此,CFD研究者们常常采用降低数值耗散的方法来构造更高精度的计算格式[1-3]。空间离散格式包含差分格式及对流通量导数的求解两部分,本文主要讨论对流通量导数计算方法的数值耗散特性,而迎风格式作为目前CFD求解对流通量的主流格式[4],成为本文的研究对象。

迎风格式主要分为三类:矢通量分裂(flux vector splitting,FVS)格式、通量差分分裂(flux difference splitting,FDS)格式以及混合格式。现今CFD对迎风格式耗散性的主要观点[5]为:以Steger-Warming格式[6]、Van Leer格式[7]等为代表的FVS格式将对流通量分裂为正负两部分,在其分裂过程中使用的简化策略诱导出过大的数值耗散,降低了格式对线性波、非线性波等的模拟精度;以Roe格式[8]、HLLC格式[9]为代表的FDS格式的基础是求解局部黎曼问题,其数值耗散较低,这使得FDS格式能够准确地捕捉到激波、接触间断等非线性波、线性波,但其在强激波处的计算稳定性较差,例如Roe格式的“红玉”现象问题;混合格式作为以上两种格式的结合,既具备了FVS格式在非线性波捕捉上的鲁棒性,也具备了FDS格式在线性波捕捉上的高分辨率,其耗散较低且稳定性优于FDS格式,例如AUSM+格式[10]、LDFSS格式[11]等。

迎风格式的数值耗散大小可表现为其对间断的捕捉能力大小。一般认为,在相同的计算条件下,捕捉到间断过渡区越窄,则格式的数值耗散越低,捕捉间断的能力越强,例如,Sod[12]、Lax[13]、Shu-Osher[14]等问题。对存在间断相互干扰的问题,则以捕捉流场小尺度结构的能力来衡量格式的数值耗散大小,在相同的计算条件下,捕捉到的小尺度结构越多、越清晰,则表明格式的数值耗散越小,例如2-D Riemann问题[15]等。不论是对间断的捕捉,还是对流场小尺度结构的捕捉,以上问题对迎风格式数值耗散的研究都集中于间断本身或间断附近,对在数值耗散作用下产生的激波间断或接触间断等对下游流场影响的研究很少。文献[16-18]在计算运动激波问题时发现,捕捉法计算运动激波会产生非物理波动,这一波动会向流场下游进行传播,进而污染激波下游区域,改变激波下游流场的结构分布,这一现象在以上三种迎风格式中都存在,但文章并未对非物理波动的产生机理进行分析。文献[19-20]采用以上三种迎风格式对马赫数为3的运动正激波进行了模拟,计算结果表明无论采用哪种格式,在激波由初始间断形成数值过渡区的过程中,在激波下游都会产生一个等熵波和一个非等熵波。这两个波在不同格式下大小不同,但始终存在,影响着激波下游流场结构分布。文献[21-22]在研究使用加权本质无振荡(weighted essentially non-oscillatory,WENO)格式计算含接触间断的可压缩流时发现,FVS格式特征值逐点分裂的不兼容性以及质量方程、动量方程、能量方程中各分量非线性离散的不一致性会导致流场中出现非物理振荡,推荐使用全局Lax-Friedrichs(L-F)分裂格式,并在WENO格式实现过程中使用一组共同的权值来消除非物理振荡。

为了进一步分析不同迎风格式数值耗散的产生机理,同时认清上文所提到的非物理波动是否与格式的数值耗散有关,采用具有单一流场结构的接触间断作为数值模拟对象开展研究。综合不同迎风格式的数值耗散及其非物理波动在接触间断问题中的表现,可以为不同的流场问题选择更加合适的计算格式。

1 控制方程与数值方法

二维笛卡尔坐标系(x,y,t)下无量纲化的守恒型Euler方程为:

(1)

式中,U为守恒变量,F、G分别为x、y方向的对流通量,其表达式为:

(2)

其中,ρ为密度,u、v分别为x、y方向的速度,p为压力,e为气体总比内能,其计算式为:

(3)

式中,γ为比热比,本文使用量热完全气体模型,γ=1.4。

采用有限差分法进行数值求解,其中时间离散采用一阶显式格式,因此方程(1)的离散形式可写成:

(4)

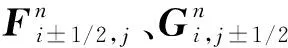
以上公式及变量皆为无量纲化的,下文数值实验中的所有变量和数据也是无量纲化的。

文中以迎风格式作为研究对象,分别选用Van Leer、Roe、AUSM+格式作为三种迎风格式的代表进行数值计算。

2 接触间断问题

2.1 一维接触间断问题

使用二维均匀正交网格计算一维流场,计算区域设定为[0,10]×[0,1],网格量为200×20。无量纲化的初始条件为:

(5)

其中,xd为间断的初始位置。将xd左侧的区域记为1区,将xd右侧的区域记为2区,因此ρ1为间断左侧的初始密度参数。

对一维接触间断问题,由之后的计算结果可以看出,在初始间断形成数值过渡层的过程中出现了非物理波动,其传播速度为特征速度,为避免扰动传出边界,设置间断的初始位置xd满足式(6):

(6)

其中,c1为1区的声速,tstop为计算终止时刻。根据初始间断左右流场马赫数的不同,即流场初始条件的不同,设置以下五个算例,其具体参数如表1所示。

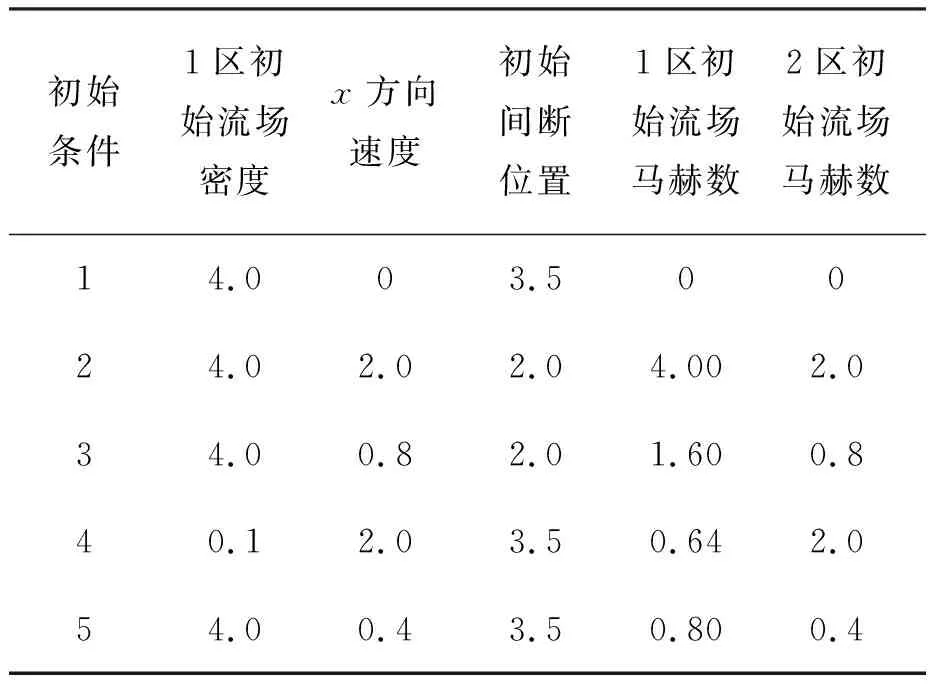
表1 不同马赫数条件下的接触间断初始条件

为计算方便,本节统一取计算终止时刻tstop=2.0,根据给定的CFL(Courant-Friedrichs-Lewy)数确定时间步长,此处CFL=0.5。此外,分别选取CFL∈{0.01、0.05、0.1、0.5}对初始条件5的流场进行计算,可知在允许范围内,时间步长的大小对计算结果影响很小,可忽略不计。

为了消除差分格式及限制器等因素的影响,选择一阶迎风格式进行数值计算,图1～5分别给出了五种初始条件下的流场参数分布曲线,包括密度ρ、速度u及压力p分布曲线。

从图1可以看出,在静止流场中,Roe格式及AUSM+格式可以完整地保持接触间断不变,其密度、速度及压力参数分布曲线皆保持初始状态。而Van Leer格式计算的流场参数分布曲线不仅有密度耗散,速度及压力曲线也有波动。

(a) 密度参数分布曲线(a) Density parameter distribution curves

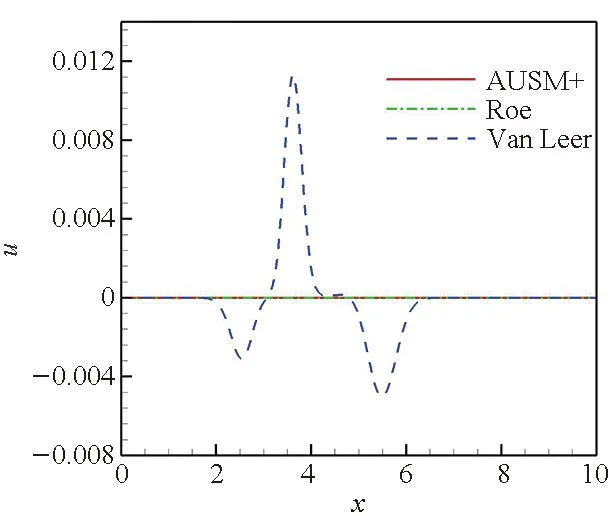
(b) 速度参数分布曲线(b) Velocity parameter distribution curves

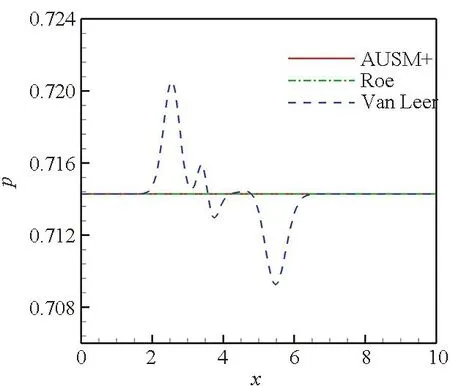
(c) 压力参数分布曲线(c) Pressure parameter distribution curves

从图2中可以看出,在流场为全场超声速条件时,三种格式对接触间断的数值模拟结果相同,都是仅有密度的耗散,速度及压力参数无变化。

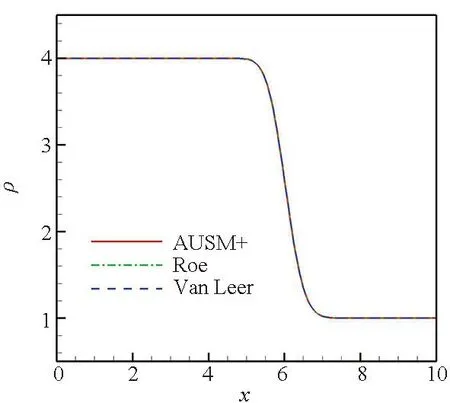
(a) 密度参数分布曲线(a) Density parameter distribution curves

(b) 速度参数分布曲线(b) Velocity parameter distribution curves

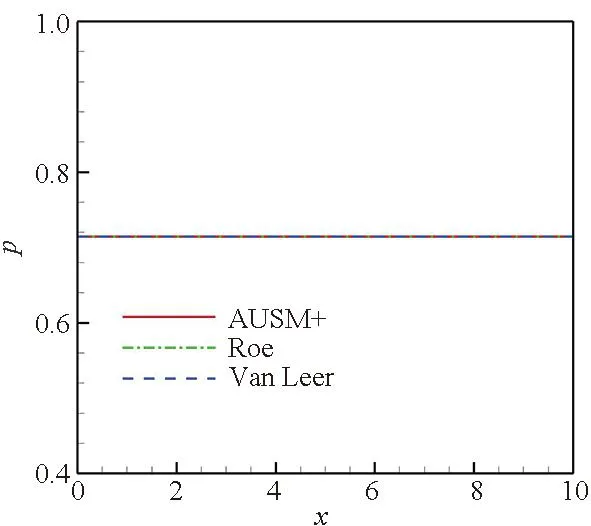
(c) 压力参数分布曲线(c) Pressure parameter distribution curves

从图3～5可以看出,在流场中存在亚声速区域时,Roe格式及AUSM+格式捕捉的接触间断仅有密度的变化,速度及压力参数无变化。Van Leer格式捕捉的接触间断存在速度及压力参数的变化,其波动曲线与在静止流场中的结果相似,不仅在间断处有波动,在间断两侧也产生了两个非物理波动。但是,尽管Van Leer格式计算的接触间断有速度及压力的变化,其密度变化曲线与Roe格式及AUSM+格式的计算结果曲线几乎重合。

根据以上算例的计算结果,对一维接触间断,Roe格式及AUSM+格式在静止流场中没有耗散,在非静止流场中有密度耗散;Van Leer格式则在所有流场中都有密度的耗散。图6给出了不同时刻静止流场(初始条件1)中非物理波动的位置变化曲线,从图中可以看出,在上文中出现的非物理波动分别以特征速度u-c1和u+c2逐步远离间断。将间断左侧波记为“波1”,间断右侧波记为“波2”,则图中v1、v2分别代表两个波动的传播速度,c1、c2分别为当地点声速。

图7给出了使用初始条件1计算的接触间断流场压力波动幅值随时间变化曲线,从图中可以看出,随着时间步的推进,诱导误差在远离接触间断的同时,其幅值大小也会逐渐降低,但不会消失。结合图6和图7可以看出,对定常问题,在计算时间足够长的情况下,误差会运动出有限的计算区域,流场结构会恢复原本的状态。但对非定常问题,波动对流场的影响无法消除,在参考文献[16-18]的算例中可以看到波动对间断下游流场参数的污染。

此外,这逐步远离间断的非物理波动不应归于Van Leer格式的数值耗散,而是一种数值误差,因为数值耗散的作用是“抹平”间断,而这两个非物理波动对密度曲线的过渡区并无影响。

(a) 密度参数分布曲线(a) Density parameter distribution curves

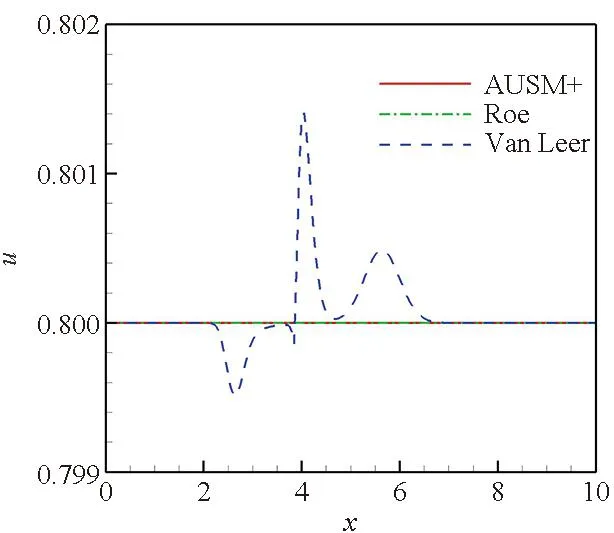
(b) 速度参数分布曲线(b) Velocity parameter distribution curves

(c) 压力参数分布曲线(c) Pressure parameter distribution curves

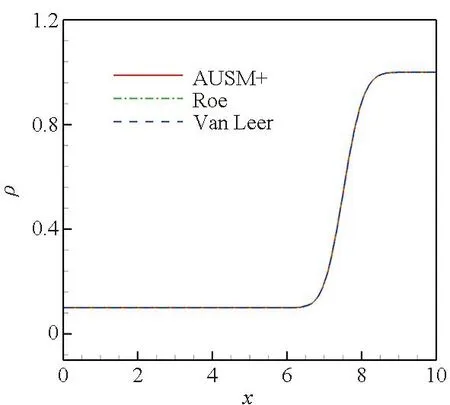
(a) 密度参数分布曲线(a) Density parameter distribution curves

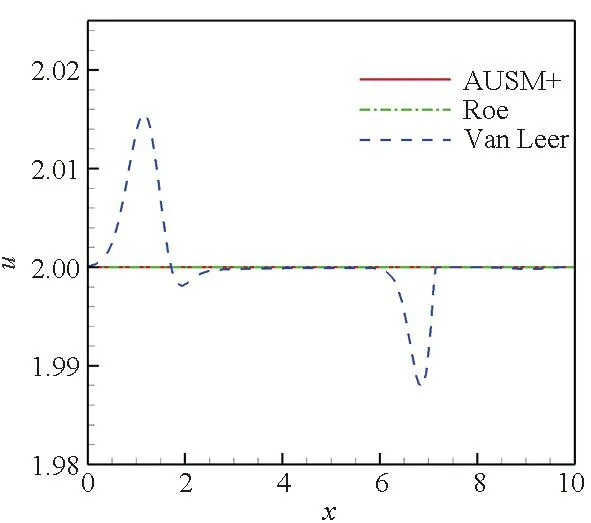
(b) 速度参数分布曲线(b) Velocity parameter distribution curves

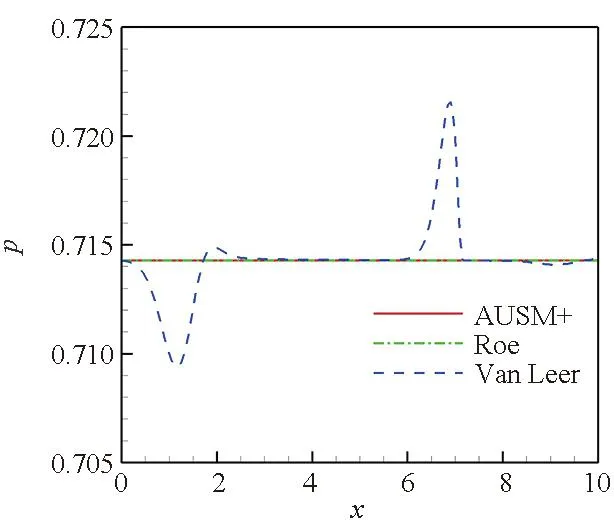
(c) 压力参数分布曲线(c) Pressure parameter distribution curves

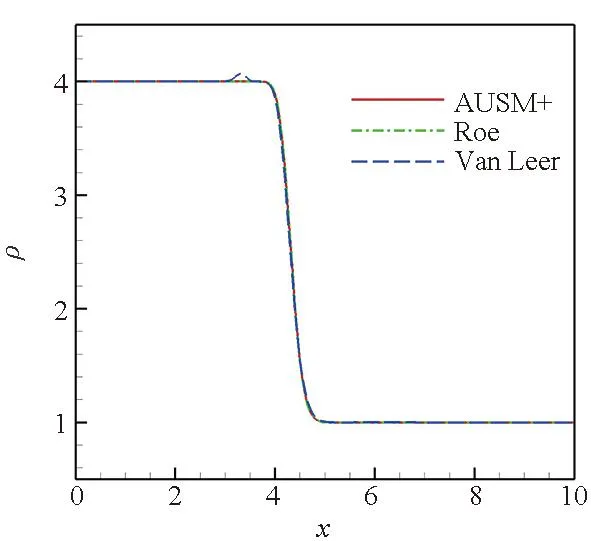
(a) 密度参数分布曲线(a) Density parameter distribution curves

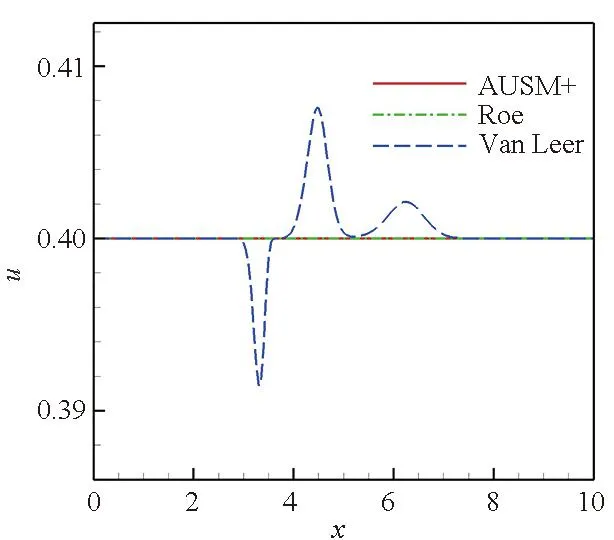
(b) 速度参数分布曲线(b) Velocity parameter distribution curves

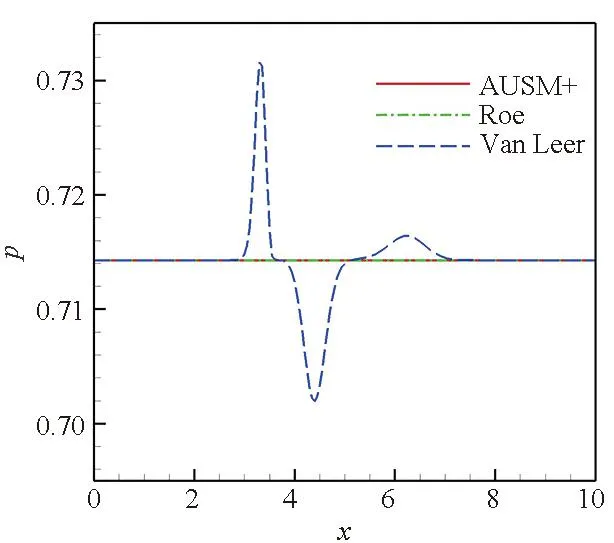
(c) 压力参数分布曲线(c) Pressure parameter distribution curves

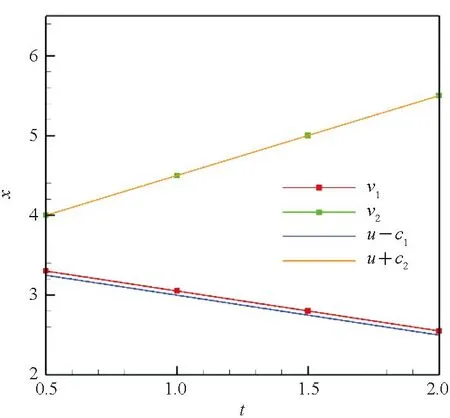
图6 波动位置随时间变化曲线(初始条件1)Fig.6 Curve of fluctuation position with time(initial condition 1)

综上所述,本文认为迎风格式的数值耗散受流场参数影响较大,在不同马赫数条件下数值耗散大小不同,不过文献[23]的计算结果也显示,在低马赫数(0.1, 0.01, 0.001)条件下,Roe格式的耗散大小与马赫数无关,而 HLL格式的数值耗散随着马赫数的减小而变大。此外,Van Leer格式捕捉接触间断时产生的非物理波动是一种数值误差,它们的存在影响了流场的速度及压力参数分布,但对Van Leer格式在接触间断问题中的数值耗散大小并无影响。

2.2 对数值计算结果的理论推导及机理分析

满足Euler方程的初始间断在计算过程中会由数学间断变成数值过渡区,按照CFD理论,一维有限差分格式的数值解在过渡区满足式(7):

(7)

因为一个网格节点无法存储两组数据,因此初始间断必占据两个网格节点。假设初始间断的中心在半节点i+1/2处(又称为界面),那么i点的初始流场参数和i-1点的相等。

对于FVS格式,一阶迎风格式离散Euler方程写成:

(8)

式中,上标“+”和“-”分别代表通量为正、负数值通量。

田志芳一个人在地窝子里，看看头顶，看看脚下，一屁股坐在土台上，叹口气，心想姆妈拼死阻拦都没拦住她和哥哥，现在怪谁呢，自己跳起脚要支边。她垂下头，把手中的沙枣花捧起来瞧，带沙点的叶根处，确实有细小的花苞，同样泛出密密麻麻的沙尘，形如青色的米粒，一粒一粒挤在一起，好似家乡中秋的桂花。猜想，沙枣花开了，是不是真有桂花那样的千里香？

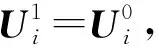
(9)

展开有:

(10)

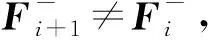
对于FDS格式,离散Euler方程后得到:

(11)

以Roe格式为例,采用存储在网格节点上的流动参数重构界面通量,一阶精度的界面通量为:

(12)

其中,广义系数矩阵A*是根据Roe平均公式计算界面处左右变量以后得到。接触间断两侧参数满足条件:ui+1=ui=u*,pi+1=pi=p*,可知界面密度变化量对动量方程和能量方程没有影响:

(13)

(14)

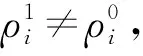
对于混合格式AUSM+,其界面通量可以写为:

Fi+1/2=ci+1/2Mai+1/2Φi+1/2+pi+1/2

(15)

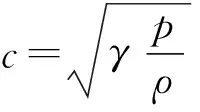
考察i+1点流场参数更新,当流场为静止流场时,半点马赫数Mai+1/2=0,且全场压力相等,因此有:

(16)

因此,在静止流场中,使用AUSM+格式计算接触间断可保持流场参数不变。

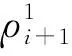
(17)

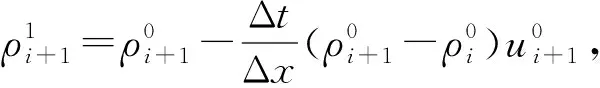
(18)

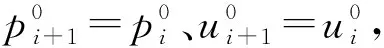
(19)

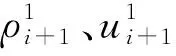
综上所述,Van Leer格式以局部马赫数为依据将对流通量分为正负两部分,在全场超声速条件下,只有正通量参与流场参数更新,对接触间断问题,虽然间断两侧密度不等致使密度参数随时间推进发生变化,产生了密度数值耗散,但更新后的密度参数对速度及压力参数无影响;在静止流场或流场中存在亚声速区域时,由于在通量分裂表达式中声速和压力、密度之间是非线性的,将更新后的密度参数代入动量方程及能量方程,流场的速度及压力参数发生改变,从而产生了速度波动及压力波动。

Roe格式计算接触间断时以密度波推动流场参数更新,同时受流场速度影响,AUSM+格式计算接触间断时同样以密度波推动流场参数更新,同时受界面马赫数(半点马赫数)影响,因此在静止流场中使用Roe格式及AUSM+格式时,流场参数无更新,自然无数值耗散产生;在非静止流场中使用以上两种格式时,质量方程参数更新,导致密度参数发生变换,产生密度数值耗散,但将更新后的密度参数代入动量方程及能量方程,速度及压力参数无变化。

同时,由以上公式推导可以看出,当初始间断的中心位于半节点i+1/2处且全场为超声速条件时,点i位于间断的上游区域,根据双曲型方程扰动不向上游传播的特性,点i处流场参数不应随时间发生变化,因此一个时间步后,Van Leer格式及AUSM+格式计算的接触间断流场,皆为点i+1处的密度参数发生变化,点i处流场参数无变化;而Roe格式计算的接触间断流场,点i处的密度参数发生变化,这显然不符合双曲型方程扰动不向上游传播的特性,这或许与“红玉”现象出现的原因有关,有待进一步验证。

2.3 二维接触间断问题

上文给出了三种不同类型的迎风格式在一维接触间断中的数值计算结果,并通过公式推导对不同计算结果出现的原因进行了分析。为了加深对不同迎风格式下接触间断的认识,给出以下二维算例。

在二维问题中,将初始接触间断放置于x方向为超声速的均匀流场中,设置计算区域为[0,2]×[-2,2],网格量为200×400。将间断放置于y=0处,初始流动参数为:

(20)

其中,ρ1=4,ρ2=1,u=2,v=0,p=1/1.4。左右边界给定超声速出入口边界条件,上下边界为一阶外推。

在本节中,首先使用一阶迎风格式进行计算,同样选用Van Leer、Roe、AUSM+三种迎风格式,时间步长按CFL=0.5计算,计算终止时刻tstop=1.5。计算结果表明,当使用Roe格式或AUSM+格式时,流场参数都能保持初始值不变,因此本节只给出了使用Van Leer格式的计算结果。图8是空间离散采用五阶WENOZ格式[24]的计算结果,此时时间离散采用具有总变差减小(total variation diminishing,TVD)性质的三阶Runge-Kutta格式[25]。图8给出了单接触间断下计算终止时流场的相对压力误差(δp=1.4Δp)分布云图及涡量(wz=∂v/∂x-∂u/∂y)分布云图。因为初始流场速度为常数,涡量为0,因此图8给出的涡量分布云图也代表了流场的误差分布。从图中可以看出,在计算过程中Van Leer迎风格式不能完好地保持间断,在间断两侧会有误差产生,误差分别以当地声速沿y方向向两侧进行传播,在x方向超声速气流的作用下形成以特征线为边界的误差分布范围。

(a) 压力误差分布云图(a) Cloud map of pressure error distribution

(b) 涡量分布云图(b) Cloud map of vorticity distribution

为进一步研究二维接触间断对流场结构的影响,设计了同时存在两个间断的流场算例。初始流场参数设置为:

(21)

其中,ρ1=4.0,ρ2=1.0,u=2.0,v=0,p=1/1.4。

图9给出了双接触间断下,在计算时间t=1.5时的流场压力误差分布云图及涡量分布云图。从图中可以看出两个间断所产生的误差在相互干扰过程中会改变每个间断的误差分布范围,且会产生复杂的小尺度结构。

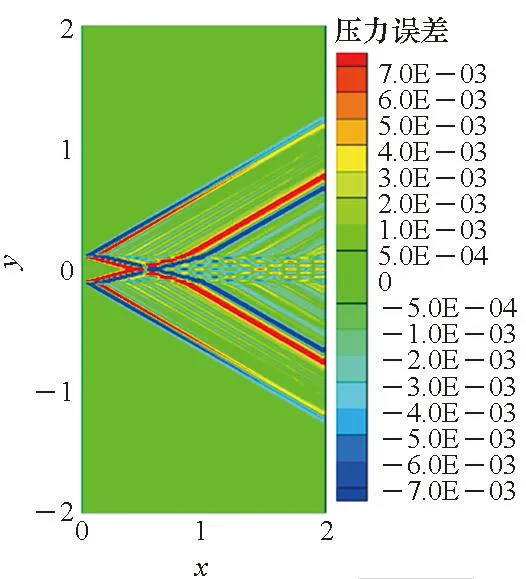
(a) 压力误差分布云图(a) Cloud map of pressure error distribution

(b) 涡量分布云图(b) Cloud map of vorticity distribution

以上算例可以看成是y方向的一维静止接触间断与x方向超声速自由流的组合问题,因为y方向速度为0,此时Roe格式和AUSM+格式对接触间断数值耗散为0,表现为流场参数保持初始值不变。而Van Leer格式在对接触间断有密度数值耗散的同时,其在间断从初始数学上的间断变成有厚度的数值剪切层时诱导出的数值误差相互干扰,会生成复杂的非物理小尺度结构,从而影响流场的结构分布。

3 线性分布流场

第2节给出了使用不同迎风格式数值模拟接触间断问题所得到的计算结果,并通过公式推导对不同结果出现的原因进行了理论分析。本节继续给了以上三种迎风格式在流场参数线性分布的流场中的计算结果。

设置无量纲计算区域为[0,1]×[0,1],网格量为100×100。给定流场密度参数为线性分布,初始参数为:

(ρ,u,v,p)=(1+y,0,0,1/1.4)

(22)

边界给初始值,即理论值。计算终止时刻tstop=2.0,时间步长按CFL=0.5(通量无分裂时CFL=0.1)计算。

首先使用一阶迎风格式进行计算,图10、图11在给出Van Leer、Roe、AUSM+三种迎风格式计算结果的同时,给出了对流通量无分裂时的计算结果。计算结果表明,在密度成线性分布的静止流场中,Roe、AUSM+格式及通量无分裂计算方法都能保持流场不变,而Van Leer格式的计算结果有较大误差产生,且该误差随计算时间增加而逐渐增大。

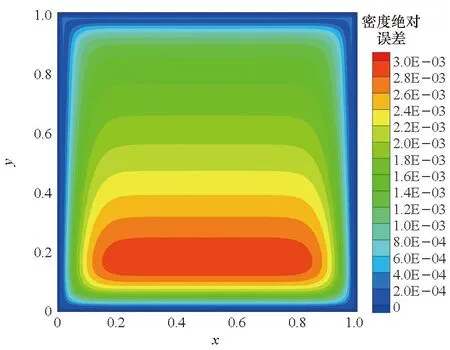
(a) Van Leer

(b) Roe

(c) AUSM+

(d) 通量无分裂 (d) Flux non splitting

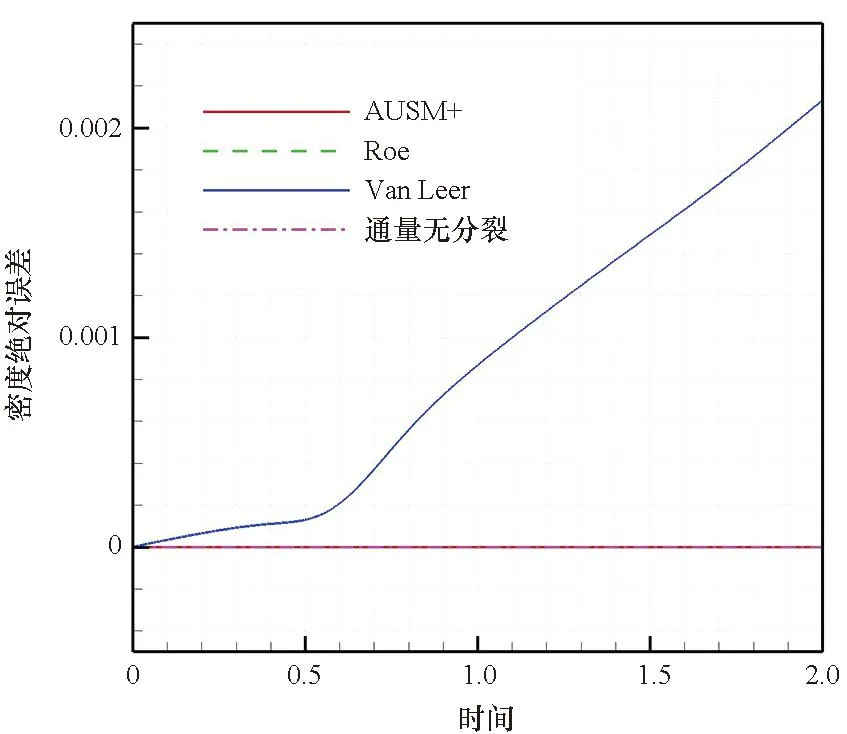
图11 中心点处密度绝对误差随时间变化曲线Fig.11 Time variation curves of density absolute error at central point

考虑到所用空间离散格式为一阶迎风格式,而此时流场为二阶精度流场,使用一阶格式计算二阶流场可能会产生误差,因此进一步使用二阶迎风MUSCL格式、五阶WCNS格式[26]和五阶WENO格式[27]对流场进行了数值模拟,计算结果如图12所示。

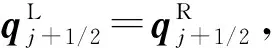
(a) 二阶迎风MUSCL格式(a) 2nd-order upwind MUSCL scheme

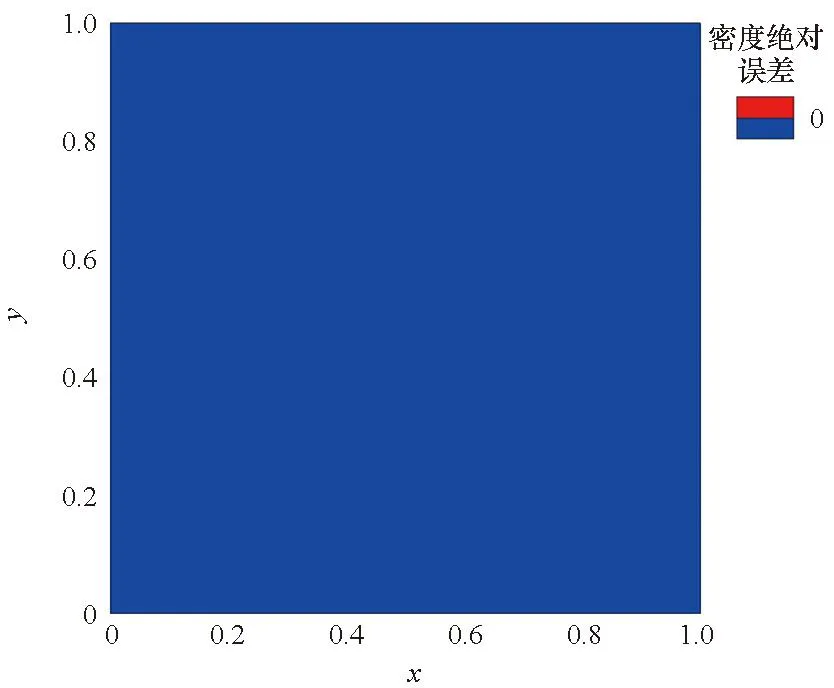
(b) 五阶WCNS格式(b) 5th-order WCNS scheme

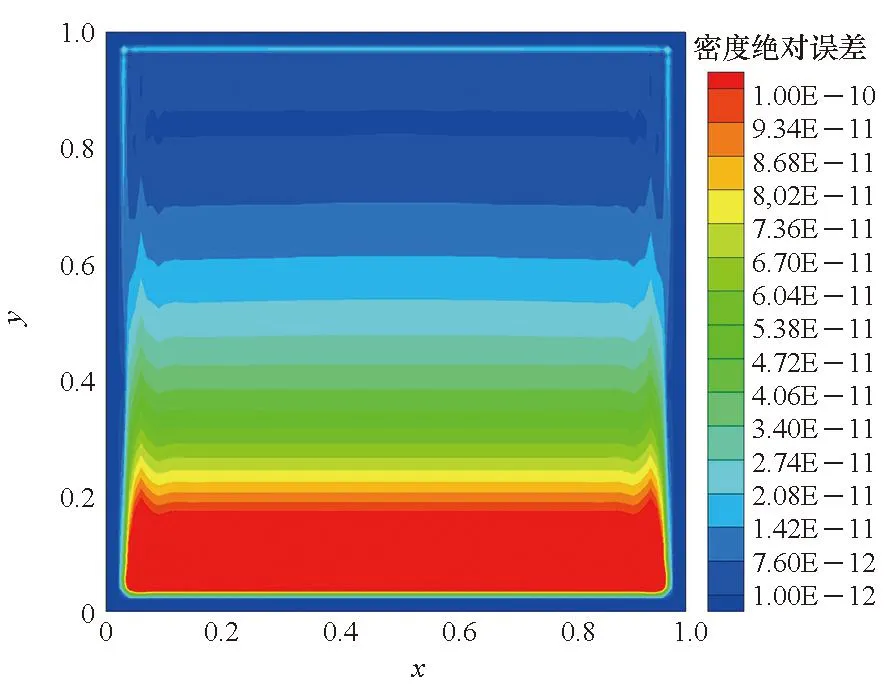
(c) 五阶WENO格式(c) 5th-order WENO scheme

从以上计算结果可以看出,Roe格式和AUSM+格式能够保持初始流场参数的线性分布不变,而Van Leer格式在空间重构对象为原始变量时可以保持流场参数线性分布不变,在空间重构对象为对流通量时则会有误差产生,破坏流场的结构分布。

4 结论

对三种迎风格式在接触间断中的数值耗散问题进行了数值实验,并通过公式推导对不同流场参数下数值耗散产生的机理进行了分析。以Roe格式为代表的FDS格式及以AUSM+格式为代表的混合格式,在接触间断问题中存在密度数值耗散,其耗散受密度差推动产生,同时受流场速度(马赫数)影响,但因为此时其质量方程和动量方程、能量方程为解耦关系,所以更新后的密度参数对速度及压力参数无影响。以Van Leer格式为代表的FVS格式在计算接触间断问题时,不仅存在密度数值耗散,在流场静止或流场内存在亚声速区域条件下,密度耗散的产生还会诱导出速度扰动误差及压力扰动误差,该扰动误差对格式的数值耗散大小无影响,但对流场结构的影响无法忽略。特别地,对L-F分裂格式,局部L-F分裂会出现以上非物理振荡误差,全局L-F分裂则不会产生非物理振荡现象。因此,文章中的FVS格式不包括全局L-F分裂格式。

FVS格式在计算一维接触间断问题时产生的诱导数值误差在二维接触间断问题中表现为复杂小尺度结构,若二维接触间断存在于复杂结构流场中,复杂小尺度结构的产生必会对流场结构分析带来困难。此外在空间重构对象为对流通量时,使用FVS格式计算密度线性分布的流场,会破坏流场参数原有的梯度,产生较大的数值误差,在高阶格式条件下,误差大大减小,但并未消除,使得流场的计算精度难以达到二阶。在空间重构对象为原始变量时,使用FVS格式可以很好地保持流场梯度。