微分法多岩性压实校正技术及其在胜利桩海地区的应用
魏新辉,陈青云
(1.中国石化胜利油田有限公司桩西采油厂,山东东营 257237;2.中国有色桂林矿产地质研究院有限公司,广西桂林 541004)
0 引言
地层压实校正是研究盆地演化史和古地貌恢复的主要内容之一。1959年,鲁贝和哈伯特提出在压实平衡条件下页岩的孔隙度随着深度的增加呈指数递减的规律(转引自袁炳存,1984年);1984年,袁炳存应用地层骨架体积不变原理对碎屑岩地层古厚度恢复进行了研究,提出了压实校正方法[1];1991年,庞雄奇等提出了基于地层质量不变原理的压实校正方法[2]。自20世纪80年代以来,许多学者对这两种函数关系进行了深入研究,提出了不少提高精度的方法[3-11]。虽然基于岩石骨架体积或质量不变原理,应用孔隙度-深度函数进行地层压实校正的思想得到普遍应用,但其拟合的数据量大,欠压实泥岩段拟合的计算方法过于复杂,地层剥蚀造成的深度差异也会导致孔隙度-深度函数关系复杂难求。更重要的是,普遍忽略了除泥岩以外的其他岩性的压实差异性,进一步导致计算结果误差较大。本文基于泥岩、砂岩和灰岩微分法压实校正研究,试图建立新的多岩性压实校正方法,提高压实校正精度。
1 微分法分岩性压实校正技术
1.1 非均质岩体微分模型
微分法压实校正技术精度高、计算简便。但实际上,地层在三维空间上各处的孔隙度不同,整体为非均质体。鉴于此,将现今埋藏深度为Z、截面积为s、厚度为H的地层等分为n(n→∞)个无穷小单元,则每个小单元可视为均质体。其厚度为:
若截面积s为:
则该柱状地层分解为由n个内部均匀的小立方体单元累积而成(图1)。设分解后每个单元的孔隙度为φ,厚度为hn,每个单元恢复到指定埋深时厚度变为Hi,孔隙度为φ0i,骨架变化量为f(φi),基于两处单元岩体的骨架体积相同,基于三点假设,每个单元体的原始沉积厚度为:
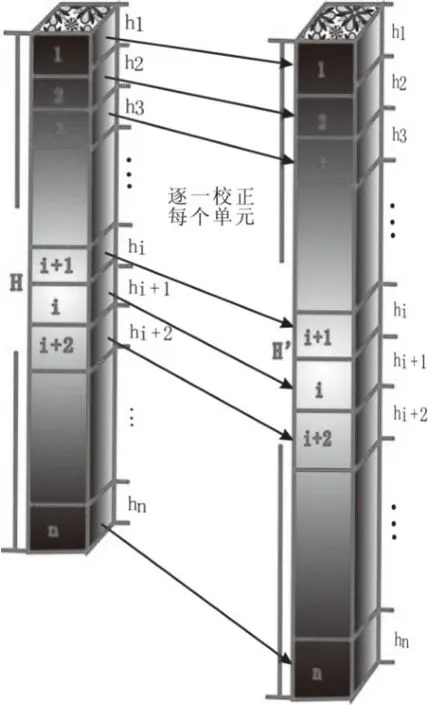
图1 地层微等分校正模型
将恢复每个小立方体的初始厚度进行累加,即为整套地层的初始沉积厚度。地层的初始沉积厚度为:
式中:H为现今埋深为Z处的地层厚度,m;H0为地层恢复至指定埋深的地层厚度,m;Hi为第i个单元体恢复后的初始地层厚度,m;φi为第i个单元体的现今的孔隙度,%;φ0i为第i个单元体恢复至指定深度的初始孔隙度,%。f(φi)为第i个单元体岩石骨架体积变化量,%。
1.2 不同岩性的压实校正模型
不同的岩性具有不同的压实规律,在地层压实校正过程中需分岩性分段计算。基于假设条件(2)和(3),可构建不同岩性的压实校正模型。
1.2.1 泥岩的压实校正模型
泥质沉积物在埋藏成岩过程中,有机质生烃、黏土矿物转化对岩石骨架体积影响小,可忽略不计,即f(φi)≈0。松散沉积物在近地表情况下主要受到压实作用,孔隙度与深度的函数关系稳定,易于求取。1959年鲁贝和哈伯特提出压实平衡条件下沉积物孔隙度和深度存在如下关系式[1]:
在地层恢复到指定的埋深过程中,仅最顶部的小立方体恢复至Z0处,设其下部第i个小立方体恢复的深度为Z0i,存在关系式:
应用式(6)可知每个微分单元的初始孔隙度为:
将式(7)代入式(4),则泥岩的压实的校正公式为:
式中:φ0为地表泥质沉积物的初始孔隙度,%;C0为地表泥质沉积物的压实系数;Z0为恢复到指定的埋深,m。
1.2.2 砂岩和灰岩的压实校正模型
前人实验研究成果表明,砂岩、灰岩的压实规律与泥岩具有相似性[12],地层孔隙度与埋深呈指数关系,因此其差异性主要表现在压实系数与泥岩不同。砂岩和灰岩每个微分单元的初始孔隙为:
式中:C为砂岩或灰岩压实系数。
由于地层在埋藏过程中,砂岩、灰岩存在胶结作用和溶蚀作用,即f(φi)≠0。当这两种作用对地层骨架改变量比较大时,需要计算这两种作用对造成的岩石骨架改变量,然后根据实际资料将砂岩或灰岩分正常压实带、胶结发育带和溶蚀发育带三个带分别计算。推导的压实校正公式分别为:
正常压实带:
胶结发育带和溶蚀发育带[当为胶结发育带时f(φi)>0,反之f(φi)<0]:
式中:f(φi)为砂岩的胶结量或溶蚀量,%,通过岩心矿物薄片估算。
2 实例应用
石炭系胜利油田桩海地区是重要的含油气层系之一,本文对其进行压实校正。
2.1 参数求取
压实校正模型的建立后,需要求取微分单元体厚度、现今地层孔隙度、恢复到指定的深度、地表压实系数、地表沉积物初始孔隙度和微分单元体骨架变化量等参数。
2.1.1 微分单元体长度hi
当前测井采样间距普遍为0.125 m,对于整套地层来说,边长为0.125 m的岩石块体可近似为均质体,因而对各井微分单元的长度取值为0.125 m,即:
2.1.2 恢复原始深度Z0
地层压实校正是将地层恢复到地表,因此有
2.1.3 地表参数C和φ0
近地表某一深度下岩石的孔隙度主要受到原始沉积物孔隙度和压实系数的影响,不同的岩性具有不同的参数,据K. A. Hegarty(1988)和漆家福(2003)[10]研究成果,泥岩、砂岩、灰岩的地表孔隙度分别取58%、43%、35%,压实系数分别取0.0007、0.00041、0.0004。
2.1.4 孔隙度求取φi
声波时差较能真实地反映地层的原生孔隙,用怀利公式或平均时间关系式求取地层各单元体的孔隙度[17]:
式中:ΔT为实测声波时差,μs/m;ΔTm为骨架声波时差,μs/m,砂岩为182 μs/m,碳酸盐岩为143 μs/m ~156 μs/m,泥岩为300 μs/m ~400 μs/m;ΔTf为孔隙流体声波时差,μs/m,泥浆为608 μs/m~620 μs/m。
2.1.5 微分单元骨架变化量
由于缺少岩心薄片资料,鉴于工区地层砂岩、灰岩厚度小,砂地比低和灰地比小,溶蚀和胶结作用造成的岩石骨架量可忽略。
2.2 基于井资料的地层压实校正实践
压实率表示地层的古沉积厚度与现今地层厚度之比,校正量表示地层的古沉积厚度与现今地层厚度之差值。当地层中存在不同岩性时,还需先划分岩性,然后依据参数求取方法及参数值,将各井资料代入压实校正公式中,即可计算各井的层位的初始沉积厚度。依据各井压实校正结果,进一步计算可得出压实率和校正量,以ZH715井为例,该井岩性为泥岩,校正前目的层厚度为58.1 m,校正后地层厚度为126.77 m,校正量为68.67 m,整个地层的压实率为2.18。
应用该方法完成了工区内关键井石炭系的压实校正计算(表1)。经统计,该区泥岩的压实率最大,为2.02~2.23之间,灰岩的压实率最小,为1.41~1.49之间;砂岩处于中间,在1.58~1.63之间。压实率不同主要受岩性、地层厚度和地层压力的影响。不同岩性的可压实性不同,其压实率也不同;同种岩性,恢复至不同埋深,其初始孔隙度不同,故压实率不同;当地层压力大,存在欠压实时,地层的压实作用变弱,压实率减小;地层厚度大,早期沉积物在地表受压实越强,压实校正后地层压实率减小。

表1 关键井的压实校正计算结果表
3 结论
1)建立的微分法多岩性压实校正技术细化了岩层内部计算单元,提高了地层压实校正计算精度。
2)影响地层压实率的因素有埋深、地层厚度、欠压实作用、砂岩和灰岩含量。
3)工区内岩性的变化和岩层厚度的横向变化是引起压实程度差异的首要原因,埋深和地层压力变化为次要原因。压实校正结果显示,泥岩、砂岩、灰岩压实程度差异较大,其中泥岩压实率为2.02~2.23,砂岩为1.58~1.63,灰岩为1.41~1.48。

