基于有限差分法深基坑支护模拟分析

寇麟兵

（连云港市金河水利工程建设监理有限公司，江苏 连云港 222000）

1 概述

水利工程施工中，深基坑开挖是重要的施工步骤，开挖过程中容易引起地表沉降、地下连续墙和基坑坍塌等系列风险，因此合理评估深基坑开挖项目的安全性十分重要[1-5]。当前，伴随计算机技术的高速发展，数值模拟方法也被广泛应用于深基坑工程中，为解决研究深基坑开挖的相关问题提供了强有力技术支撑[6，7]。目前国内外对深基坑数值模拟方法进行了大量研究，取得了一系列成果。李伟沛[8]利用FLAC 2D 程序，采用显式有限差分法，分析了受向上渗流作用围堰内砂土的渗透破坏；徐冉[9]建立有限元模型，主要分析了基坑开挖过程中土体沉降及支护结构变形；杨本健等[10]以江苏某商业项目基坑为工程背景，利用MIDAS-GTS 数值模拟软件，对以钢管桩为支护体系的基坑进行数值模拟，对6种不同直径的管桩进行开挖模拟；郑华[11]以填埋基坑为研究对象，采用现场实测与数值模拟相结合的研究方法进行填埋基坑变形及稳定性的研究；黄广龙[12]为研究基坑开挖结束后竖向位移的变化，通过数值模拟技术，对5 种不同工况下的施工方案进行研究。此外，还有部分学者采用有限元、有限差分等方法对深基坑开挖进行了模拟[13-15]。

本文以某深基坑项目为例，采用最新的Plaxis 3D 软件对深基坑进行建模分析，对比分析了不同开挖工况下基坑渗流、地下连续墙变形以及地表沉降规律，研究成果可为相关工程提供参考。

2 工程概况

本文研究的深基坑项目历年最高气温为36℃（1962年8月28日），历年最低气温为0℃（1961年1月9 日），低温天气多出现在1 月，高温天气多出现在8月。该工程基坑深度大，最大高差达到15 m，且情况复杂，底部存在大量淤泥、粉细砂，水位差比较大，水位变化快。初期排水时间定为2～4 d，拟采用3 台中联潜污泵排水，水泵型号为100QW110-10-5.5（流量110 m3/h，扬程10 m）。基坑开挖顺序先箱涵防洪闸基础，其次泵房主体基础，其余基础调节施工。

3 数值模型建立

本次建立的数值模型采用对称建模方法，开挖的水平尺寸为I/b=20/18 m，地下连续墙的厚度为80 cm，平面如图1 所示。开挖基坑周围有相邻表面荷载，与外部荷载（q=200 kN/m2）和板基础（q=80 kN/m2）相比，中间条形基础最高集中荷载q=250 kN/m2。此外，基坑主要支撑方向与短边平行（b=18 m），所有计算都是通过定位支柱和壁板进行。地下连续墙的施工深度为-28 m，最终开挖标高为-17 m，地表以下3～4 m 处存在地下水。开挖顺序包括5 个开挖步骤，中间开挖层以及4个支柱层如图2所示。三维模型的尺寸为x/y/z=50/60/60 m，边界条件的影响可以忽略不计。有限元模型中连续单元由10 个节点四面体单元组成，对应于位移的二阶插值，地下连续墙由单独的混凝土截面组成。

图1 开挖平面

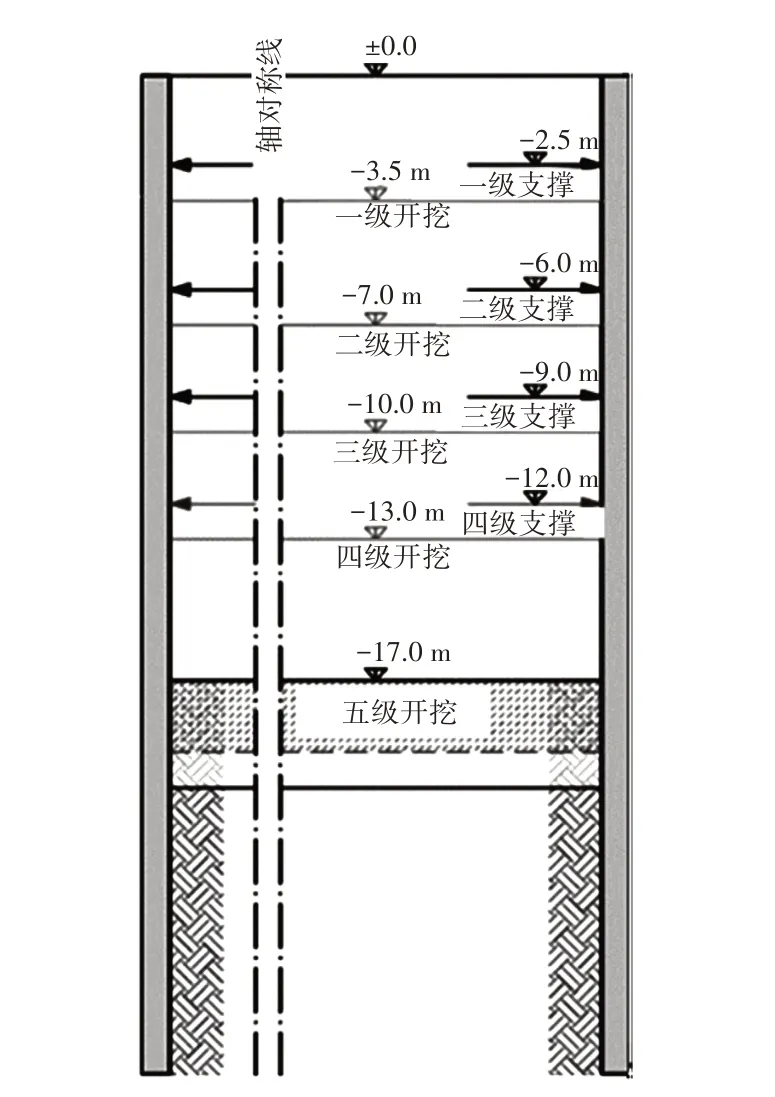
图2 开挖步骤及支护

本次计算土体采用具有小应变刚度的硬化土体模型进行建模，土体材料分为3 层，分别为回填土、粉土和黏土，模型为莫尔-库仑模型。对于混凝土地下墙和钢构件，采用弹性模型。与弹性模型相比，使用硬化土（HS）的优势在于控制刚度参数，包括切线固结仪模量、割线三轴模量E50、卸载-再加载模量。本次建立的数值模型如图3 所示，数值计算参数详见表1。

表1 土体参数

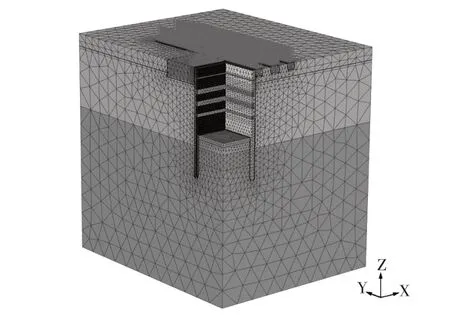
图3 数值模型

4 数值结果分析

4.1 基坑开挖渗流分析

施工期间，尤其是在开挖水平以下，孔隙应力会变为负值，这会导致土壤强度增加。负超孔隙压力越高，产生的墙体变形和应力以及表面沉降越低。不排水条件下开挖到最终阶段产生的超孔隙水压力，如图4（a）所示。负超孔隙压力的产生取决于卸载量、不同的土壤参数和初始应力状态。由于最终开挖水平面附近邻近土壤参数的变化（Z=-20 m），因此排水和排水条件边界（Z=-18 m）不一定会出现最大值。最大负超孔隙压力约为190 kN/m2，出现在开挖区域中心，低于最终开挖标高z=-20 m（第三层土层开始处）。此外，开挖区域内向隔水墙方向出现了负超孔隙压力降低的趋势，这与墙变形量增加有关。墙体发生移动与土体所经历的水平荷载相关，墙后的土壤会经历卸载，导致墙后产生负的超孔隙压力，尤其是在墙变形最大的地方。此外，还进行了耦合分析，即在2 周时间内对每个开挖步骤进行固结。此种方案的最大负超孔隙压力（耦合1 表示在开挖后进行固结、最大值为49 kN/m2，耦合2 表示在开挖期间进行耦合分析、最大值为56 kN/m2）大约比不排水条件下低4倍，如图4（b）所示。

4.2 地下连续墙位移分析

不同排水条件下的地下连续墙水平位移，如图5 所示。从图5 可以看出，在墙角处，不同的排水条件实际上对其变形没有影响，此时变形的差异可以忽略不计；但在墙体中部以下，开挖排水条件对墙的影响十分显著。水平方向耦合方案1 和耦合方案2的墙体位移计算结果介于不排水和排水计算之间，不排水和固结计算的结果之间的差异十分明显。一般而言，由于开挖产生负超孔隙压力导致土体强度增加，不排水条件下的墙体变形低于排水条件下的墙体变形。因此，与不排水条件相比，由于负超孔隙压力降低而引起的额外墙体移动，排水条件下支柱会承受更高的应力，所以支柱需要在不排水条件下的先前步骤中安装。

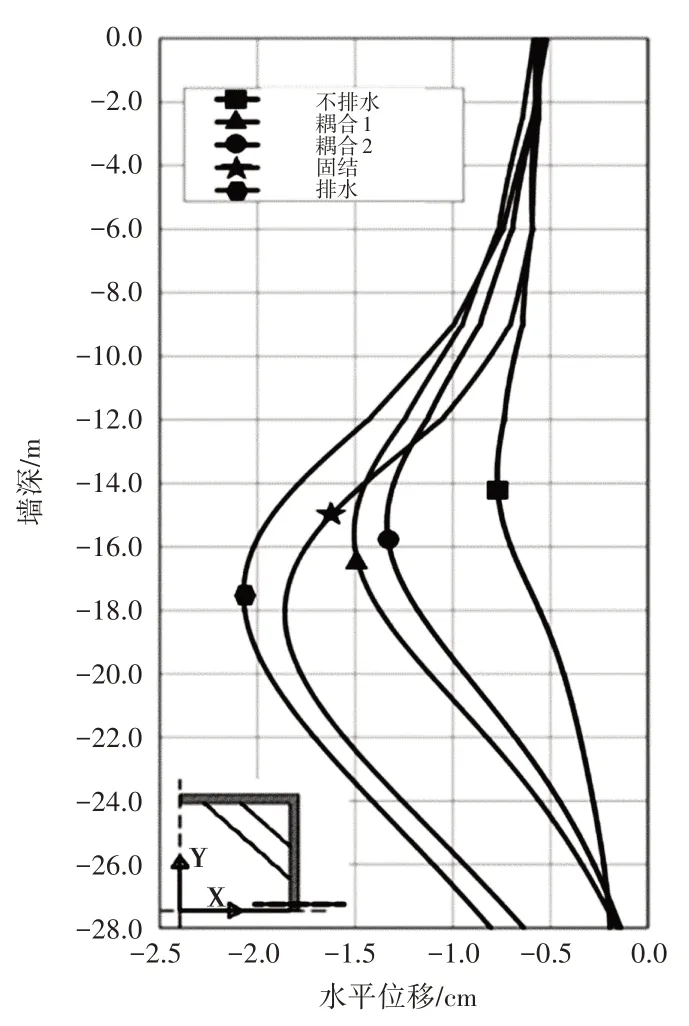
图5 数值模拟与探头1的水平位移检测结果

4.3 地表沉降分析

距离墙体不同距离下地表沉降规律，如图6 所示。从图6 可以看出，随着表面荷载与墙体距离的增加，地下连续墙后受影响区域的深度也同时增加，但由于土壤中附加应力的变化，水平方向影响区域逐渐减小。因此，可以看到虽然排水条件不同，但墙后变形趋势却大致相同，墙后的沉降与上部区域的墙挠度相对应。其中，在距离墙体5～10 m，地表的沉降量最大，大于1.2 cm；而在20 m 以后，地表沉降几乎可以不计。此外，耦合计算产生的地表沉降位于排水条件和不排水条件之间。随着与墙体的距离增加，最终固结方案产生的沉降将大于耦合方案，这与在最终开挖标高周围观察到的墙体变形相同。

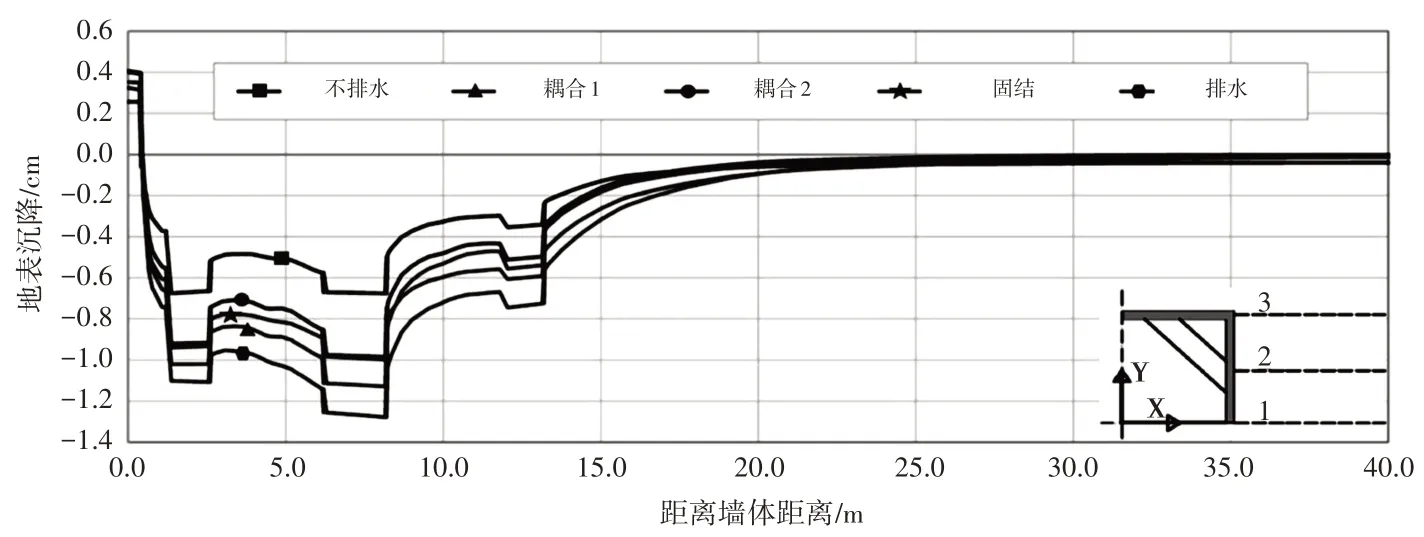
图6 距离墙体不同距离下地表沉降规律

5 结论

本文以某基坑项目为例，采用最新的Plaxis 3D软件进行建模分析，对比分析了不同开挖工况下基坑渗流、地下连续墙变形以及地表沉降规律。结果表明，基坑最大负超孔隙压力约为190 kN/m2，出现在开挖区域中心，低于最终开挖标高z=-20 m（第三层土层开始处）。此外，开挖区域内向隔水墙方向出现了负超孔隙压力降低的趋势。在墙角处，不同的排水条件对墙角变形没有影响；但在墙体中部以下，开挖排水条件对墙的影响十分显著，距离墙体5～10 m，地表的沉降量最大，大于1.2 cm；而在20 m 以后，地表沉降几乎可以不计。