基于时域编码超表面脉内-脉间编码优化的雷达干扰方法

许 恒 许 红 全英汇* 潘 秦 沙明辉 陈 珲 程 强 周小阳

①(西安电子科技大学电子工程学院 西安 710071)

②(西安市先进遥感重点实验室 西安 710071)

③(西安电子科技大学杭州研究院 杭州 311200)

④(北京无线电测量研究所 北京 100854)

⑤(东南大学毫米波国家重点实验室 南京 211189)

1 引言

雷达是在战场中掌握制信息权的探测装备。而如何保护己方高价值目标，降低敌方雷达获取信息的能力是电子战的重中之重。现有的有源干扰可以通过动态调整干扰参数，形成压制或者欺骗的干扰效果。典型的干扰样式有灵巧噪声干扰、移频转发干扰和间歇采样转发干扰等。其中，现有基于数字射频存储(Digital Radio Frequency Memory,DRFM)的采样转发干扰，可以通过发射与雷达波相参的干扰波形并施加调制，实现精细化干扰。然而，由于雷达探测与抗干扰手段的不断进步与升级[1,2]，传统与干扰技术已经逐渐不能满足反雷达需求，亟需对其进行技术变革。

2010年以来，超材料技术的发展为无源干扰提供了新思路。该技术通过设计单元中的亚波长介质实现具有超常物理特性的人工复合结构，可以显著减小雷达散射截面积(Radar Cross Section,RCS)，实现低功率反射。超表面是一种具备对入射电磁波在能量域、频率域、极化域、空间域、相位特征等多域联合电磁调控的新型可重构超材料，是研究热点之一，在无线通信、智能感知等领域有广泛的应用前景[3−11]。

数字编码超表面通过电控形成两种状态，分别表示为“0”和“1”。经过该单元两种状态的反射电磁波相位响应在某频率处具有180°相位差。数字编码超表面还可以设计为多比特状态，例如，当该单元为2比特时，其状态字分别为“00”“01”“10”“11”，且反射波相位差分别为0°,90°,180°和270°。该技术已经可以应用在以相位匹配为核心处理的脉冲多普勒体制雷达干扰中。例如，面对窄带雷达探测，将一半单元置为“0”状态，另一半单元置为“1”状态，则能够实现后向反射信号对消。2016年，国防科技大学冯德军团队的张然[5]提出并验证了一种人工电磁结构—相位选择表面(Phase-Switched Screen,PSS)应用于电子对抗的效应，通过脉内相位快速变化能够在脉冲压缩后形成对称假目标，甚至可以将雷达信号调至接收机带外形成RCS缩减效果。同年，该团队提出了一种基于PSS时域调制的合成孔径雷达(Synthetic Aperture Radar,SAR)微动多普勒干扰。2018年，Dai等人[8,12]提出了时域超表面的概念，增加了超表面的调控维度，同时实现了电磁波频谱调控等新特性。2022年，中国科学技术大学Li等人[13]提出了一种基于时域调制超表面部分覆盖的逆合成孔径雷达(Inverse Synthetic Aperture Radar,ISAR)成像干扰，分析了超表面干扰在实的应用场景中的效用。文献[14]分析了时域编码超表面对窄带雷达探测的影响，推导了回波频谱特性，系统地解释了其对雷达形成和欺骗干扰的原理。文献[15]提出并实现了一种基于时空编码超表面非线性周期相位调制的脉内调频连续波信号的生成与调控方法，为其在雷达系统中的应用提供了新的解决思路。

国外学者正逐步开展对超表面在雷达领域的应用研究。2019年，澳大利亚国立大学Shadrivov团队[16]提出了一种宽带可切换超表面，通过在时域进行伪随机调制，将入射雷达窄带信号扩展为宽带频谱，进而实现伪装。2021年，加拿大蒙特利尔理工学院Caloz团队[17]提出了基于超表面时域调制的雷达扩频方法。该方法利用二极管控制超表面形成周期性的伪随机噪声序列，导致雷达回波频谱扩展，功率谱密度急剧下降。同时，该友方雷达可以通过该调制序列进行信号解调恢复信息。同年，Kozlov等人[18]从雷达信号处理角度，通过动态调整雷达入射波的反射相位，将目标多普勒搬移至零频附近，补偿目标运动的真实多普勒信息。该方法使受超表面调制的目标回波经过雷达杂波抑制处理时被滤除，进而实现目标对雷达隐身。此外，宽带电磁散射、大角度电磁散射、曲面工艺等技术也正得到大力发展，这使得超表面在雷达干扰领域的应用趋向稳健和成熟。

超表面电磁调控可以通过改变回波特征，影响雷达信号处理输出，缩减敌方雷达对保护目标的探测能力。相比于现有的有源干扰，超表面能够零延时地直接反射经过调制的雷达回波，实现“隐真示假”。国外已针对雷达探测的各个环节研究超表面的布设方式、调控策略等，但目前国内的研究大多是从目标特性、宽带成像等角度出发，设计低RCS超材料单元，分析基于随机编码、周期编码等简单调制的超表面对雷达探测的影响，而对超表面如何影响窄带雷达探测、超表面如何进行精细化调控最大化对雷达的干扰效能等问题的研究尚属空白。

本文提出了一种基于时域超表面脉内-脉间编码优化的雷达干扰方法，其中雷达与超表面的交互示意图如图1所示。首先，推导并分析了超表面对窄带雷达探测的影响效应，然后建立优化模型并求解脉内-脉间最优编码策略，最后通过仿真实验对其进行验证分析。

图1 雷达与时域超表面交互示意图Fig.1 Schematic diagram of radar interaction with time domain metasurface

2 时域超表面电磁调控与脉冲多普勒雷达响应模型

超表面是一种可以通过其内部结构改变入射电磁波散射特性的功能材料，定义超表面的后向反射系数为

其中，A为幅度系数，φ为相对相位系数。式(1)所示的反射系数指在某一时刻超表面对入射电磁波调制的幅度与相位，又由于幅度调制对雷达信号处理影响较小[5]，本文忽略式(1)中幅度系数，并令A恒等于1。而受限于硬件技术，超表面现阶段难以实现精细化相位调制，因此借鉴文献[11]用比特数表示超表面可调离散相位数量的形式。在本文中，设定1比特与2比特调制的离散相位集合Φ为典型值[0 π] 与[0 π/2 π 3π/2]。

假设超表面为2比特相位调制如图2所示，其在原始信号每个宽度为Tc的时间片中对入射电磁波叠加该时间片对应的相对相位φ，即超表面在时域中每经过Tc进行一次反射系数变换，则其对入射电磁波的调制函数可以表示为

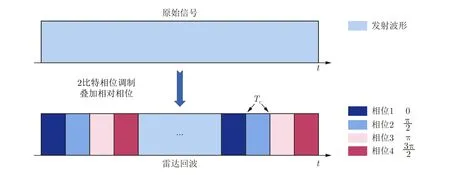
图2 超表面2比特相位编码调制示意图Fig.2 Schematic diagram of metasurface 2 bit phase coding modulation

其中，Ri为超表面在第i个时间片的后向反射系数，g(·)为宽度为Tc的门函数。进而，经过超表面调制的回波信号可以表示为

其中，s(t)为未调制的雷达回波信号。

针对脉冲多普勒体制雷达发射线性调频(Linear Frequency Modulation,LFM)波形，脉宽为Tp，带宽为B，每段脉冲包含Mt个超表面调制时间片，发射脉冲数为N，脉冲重复间隔为Tr，则经过超表面调制的多脉冲回波基带表达式可以写为

其中，Rn,m为第n个脉冲回波中第m个时间片的超表面调制系数，K=B/Tp为LFM波形的调频斜率，τ为目标距离导致的回波时延，fd为多普勒频率。

根据傅里叶变换性质，式(3)在频域的对应表达为

其中，DFT[·] 为离散傅里叶变换，S(f)为LFM脉冲信号频谱，R(f)为超表面调制函数频谱，⊗为卷积运算符。因此，受调制回波频谱本质上为LFM频谱按R(f)离散采样各频点幅度进行加权搬移并叠加，而调制函数映射到频域可以表示为

对于简单周期编码调制序列，R(f)表现为对辛格函数的对称或非对称的周期性采样。图3(a)为无调制的线性调频回波时频图，当超表面以 (0,π)为周期进行相位编码调制，调制函数时频图如图3(b)所示，其频率峰值以零频为中心向两侧进行等间隔搬移并叠加对称的幅度衰减向外侧扩展。当超表面以(0,π/2,π,3π/2)为周期进行相位编码调制时，调制函数时频图如图3(c)所示，其频率峰值位置以非对称等间隔的形式铺满采样空间，且峰值幅度同样非对称。

图3 超表面调制的LFM回波时频图示意图Fig.3 Time-frequency diagram of LFM echo with metasurface modulation

由于LFM信号具有距离多普勒耦合特性[19,20]，经过周期相位调制的LFM回波在匹配滤波后会形成间隔相等的假目标。另外，根据式(6)可得，扩频后峰值频率幅值包络为Tc·(sin(πfTc)/(πfTc))，衰减为归一化相位矢量求和项，则雷达可以通过匹配滤波假目标间隔、幅度衰减关系等参数定量反演超表面编码序列，进而对回波进行解调，以恢复目标真值。上述干扰方法能够在特定位置形成欺骗干扰，但受调制回波及其匹配滤波结果具有较强的调制特征，易被雷达检测识别并提取调制参数。

3 基于相位编码优化的距离多普勒联合欺骗干扰

由于简单周期编码频谱及匹配滤波结果在欺骗干扰附近会出现规律性谐波分量，目标存在被识别并探测的风险。而理想的欺骗干扰是将回波信号处理后目标位置的能量搬移至预定位置形成单峰，并避免规律性的干扰旁瓣。对于较短的相位编码序列，虽然通过数值计算可以验证经过该调制的回波脉压结果是否满足干扰需求，但序列长度限制了回波调制的自由度，难以实现良好的干扰效果。而对于较长的相位编码序列，其对应的回波脉冲压缩、相参积累结果中各点幅度都与编码序列相位矢量和相关，其计算量和求解过程是非常庞大且复杂的。因此，本文采用基于编码优化的方法对最优相位调制序列进行求解。针对回波经过脉冲压缩、相参积累形成的二维距离-多普勒图，由于优化变量为整个相参处理间隔(Coherent Processing Interval,CPI)中全部时间切片的相位，其优化过程计算资源消耗庞大、收敛速度缓慢，且对于高分辨率相位调制，其计算量呈数量级增长。本文将超表面多维调制编码进行解耦，分别对快时间域、慢时间域编码进行优化求解并在时域进行编码合并，最终呈现距离多普勒联合欺骗干扰。

3.1 快时间域相位编码优化

假设雷达发射LFM波形为

其中，M为信号长度，C 表示复数。

假设超表面相位调制序列，即快时间域反射系数序列为

其中，rk=ejφk，且φk ∈[0,2π)。根据式(3)，经过超表面反射的雷达回波序列可以表示为

其中，

假设匹配滤波器系数为

则经过超表面相位调制的回波脉冲压缩结果为

其中，H ∈C(2M−1)×M为匹配滤波卷积矩阵，可以表示为

由于超表面时域相位调制本质上是对入射信号进行频移，进而改变匹配滤波后的能量分布，所以3.1节优化方法的目的是使预设位置的欺骗干扰能量最大，同时使目标真实位置的能量小于雷达检测门限。而例如间歇采样转发干扰等有源干扰，发射大功率干扰信号，其在频域往往存在较高旁瓣，并以此遮盖目标。相比之下，本文所提欺骗干扰方法是无源的，经过超表面调制的回波能量有限。因此，为了使干扰被有效检测，根据能量守恒定律需要对干扰旁瓣进行抑制。

假设在p ∈C(2M−1)×1中设置距离欺骗干扰位置为j ∈[−M,M]，则可以建立优化模型：

其中，Dj为除干扰位置j及其主瓣的值为1其余位置均为0的对角矩阵，D0为除中心元素的值为1其余位置均为0的对角矩阵，∥·∥p表示向量的p-范数，I为单位矩阵，nc为目标检测参考单元点数，Dc为除目标检测参考单元位置的值为1其余位置为0的对角矩阵，α为权重系数，η为目标检测阈值，φ(·)为待优化变量相位。在式(14)中，目标函数的第1项为经过相位编码序列r调制的雷达回波匹配滤波结果的旁瓣峰值能量与干扰峰值能量之比，通过最小化该分量能够使干扰旁瓣区域平坦并避免非理想的尖锐峰值出现。目标函数的第2项为经过r调制的雷达回波匹配滤波结果的积分旁瓣能量与干扰主瓣能量之比，通过最小化该分量能够使匹配滤波输出能量向干扰主瓣聚集，进而降低整体旁瓣水平。式(14)约束条件中的第1式旨在约束真实目标位置能量与目标检测参考单元位置的平均能量之比小于检测阈值，通过该约束确保目标位置能量消隐以避免被有效检测。综上，该模型通过最小化旁瓣能量与干扰能量比、峰值比，并约束目标真实位置的检测阈值与相位编码恒模条件，使匹配滤波后形成单峰假目标。

3.2 慢时间域相位编码优化

雷达回波的多普勒信息通常是通过慢时间频率滤波来提取的，而要形成多普勒欺骗效应，则需要在脉间引入相应频率的相位差。假设每个距离单元上多脉冲序列为

则在脉冲串中的相同距离单元经过相参积累的滤波结果为

其中，F为N点离散傅里叶变换矩阵，可以表示为

其中，WN=e−j(2π/N)。

假设超表面慢时间域调制序列为

则经过超表面调制的慢时间域滤波结果可以表示为

其中，

假设预设欺骗干扰位于第i个多普勒通道，则超表面慢时间相位调制序列优化可以建模为

其中，Di为除干扰位置i的值为1其余位置均为0的对角矩阵，β为权重系数。式(21)中各项物理含义与式(14)相同。

经过该优化过程得到的最优变量s能够使预设多普勒通道的滤波结果形成突出峰值，且其余多普勒通道幅值分布较为平坦，形成多普勒假目标，实现速度欺骗干扰。

3.3 多域联合相位编码

多域联合相位编码调制是指通过在整个雷达CPI中进行长时间调制，对脉内匹配滤波、脉间相参积累过程中均形成一定的影响。基于编码优化的方法可以求解脉冲串中每个时间切片的调制相位，实现在距离-多普勒图中任意位置形成欺骗干扰并消隐原始目标能量。然而，在二维求解该问题时待优化变量的数量成倍增加，约束条件相对于一维模型更加严格，导致计算复杂度增加、搜索空间扩大、全局最优可行解求解困难。而将二维优化模型解耦，进而分别对两个一维优化模型进行求解的思路能够大幅降低其计算资源，虽然缩减了目标函数关注的解空间，没有实现二维图中无起伏的低旁瓣，但其形成的距离-多普勒二维欺骗干扰依然是有效的。

假设由多脉冲堆叠的雷达CPI内脉冲串矩阵可以表示为

则经过快时间-慢时间域联合相位调制的回波矩阵可以表示为

即调制序列矩阵为

由此，雷达回波脉冲串分别经过快时间域、慢时间域两次独立相位调制，能够在距离-多普勒图中形成任意位置的欺骗干扰，大幅降低了雷达的探测威胁。

3.4 相位编码优化求解

根据式(14)和式(21)优化模型中的约束条件，该问题具有离散特性，且其目标函数与恒模约束均为非凸函数，这使得传统的数值优化方法在求解时可能会受到限制。遗传算法是一种具备全局搜索能力的启发式算法，该算法在处理复杂离散问题时性能良好。因此，本文采用遗传算法对离散相位的超表面调制序列进行优化，该求解方法步骤如图4所示。

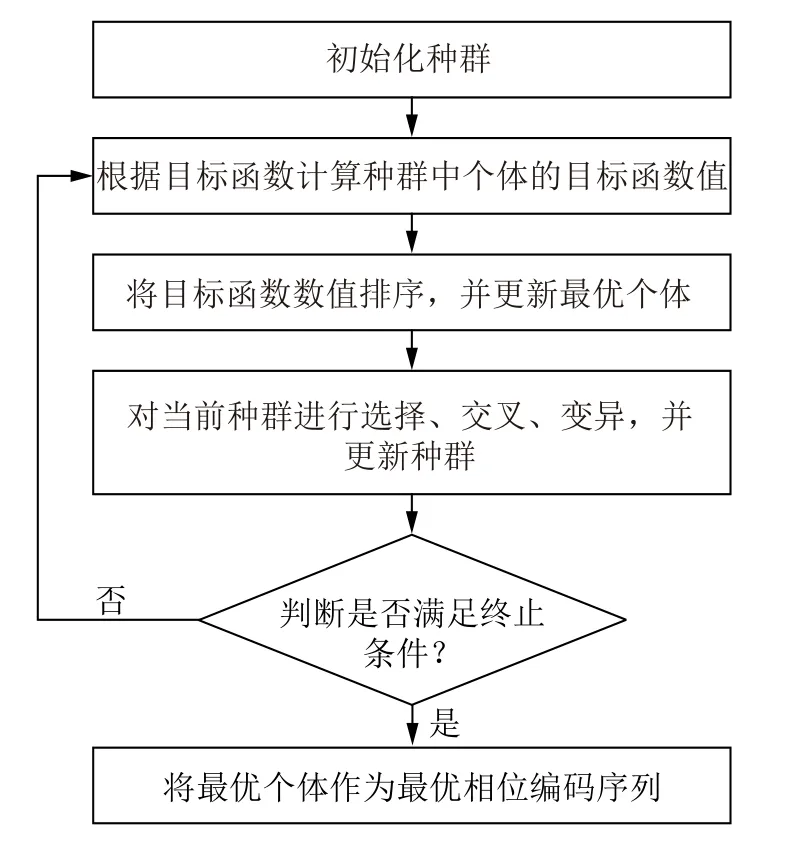
图4 相位编码优化求解流程图Fig.4 Flow chart of phase coding optimization solution

3.5 计算复杂度分析

式(14)所示的快时间域优化模型，其每一项中HXr的计算复杂度为O(M2)，求各点能量与取范数操作的计算复杂度均为O(M)，即快时间域优化模型每迭代一次所需的计算复杂度为O(M2)。同理，式(21)所示的慢时间域优化模型，在不考虑快速算法的情况下，其每一项中FYs的计算复杂度为O(N2)，求各点能量与取范数操作的计算复杂度均为O(N)，即慢时间域模型每迭代一次所需的计算复杂度为O(N2)。3.1节—3.3节所提优化模型是两次优化，其综合计算复杂度可视为O(M2+N2)。然而，二维全局优化模型是先对脉内匹配滤波再对脉间进行多普勒滤波，该模型每迭代一次所需的计算复杂度为

因此，本文所提方法大幅缩减了算法迭代过程中的计算复杂度。

4 仿真实验

为了验证基于脉内相位编码优化的欺骗干扰有效性及其干扰性能，本文设计了5组仿真实验，采用MATLAB软件分别对不同优化模型、不同干扰距离和不同输入信噪比进行了仿真对比分析，并对不同雷达波形进行验证。雷达工作在X波段，脉内波形调制为LFM，具体波形参数如表1所示。

表1 雷达波形参数设置Tab.1 The parameter setting of radar waveform

优化模型采用遗传算法进行求解，该算法的参数设置如表2所示。

表2 优化模型求解算法参数设置Tab.2 The parameter setting of the optimization model solution algorithm

4.1 仿真实验1 基于LFM波形的脉内脉间编码优化仿真实验

假设目标径向距离为3000 m，径向速度为100 m/s，干扰距离为900 m，干扰速度为–100 m/s，超表面2比特调制，其相位调制裕度为(0°,90°,180°,270°)离散相位集合，超表面调制周期(时间切片Tc)为100 ns，输入信噪比为0 dB。仿真实验1根据3.1节—3.3节阐述的优化编码策略分别对快时间域、慢时间域编码进行优化，旨在验证所提干扰方法的有效性。

图5(a)为雷达回波单脉冲脉压结果，雷达原始回波经过超表面的脉内相位调制在快时间域脉压结果中3907.5 m处形成假目标，且原目标位置能量被噪声淹没，该干扰峰值相比于未调制回波脉压峰值降低了3.30 dB，但仍具有较大干噪比，能够在快时间域形成有效的欺骗干扰。图5(b)为快时间域调制模型的算法迭代曲线，在1000次迭代以内达到高水平的干扰峰值与旁瓣最大值幅度比，并后续迭代进行微调。

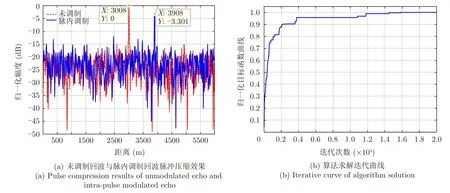
图5 快时间域相位编码优化欺骗干扰Fig.5 Phase coding optimization of deception jamming in fast time domain

图6(a)为雷达回波脉冲串单距离单元多普勒滤波结果，经过超表面脉间调制，雷达回波多普勒频率得到搬移，并在零速度处形成速度欺骗(298.83 m/s处峰值为部分经过重频折叠后的能量)。相比于快时间域的信号处理过程，慢时间域的编码优化相对简单，干扰能量衰减较小，且优化算法收敛速度更快。图6(b)为慢时间域调制模型的算法迭代曲线，由于该域滤波的信号处理流程较简单，模型优化的收敛速度也大幅提升。

图6 慢时间域相位编码优化欺骗干扰Fig.6 Phase coding optimization of deception jamming in slow time domain

图7(a)为未调制回波脉冲串脉冲压缩和相参积累形成的距离-多普勒图。如图7(b)所示，将快时间域、慢时间域相位编码优化得到的最优结果进行乘积，形成脉内-脉间联合编码，实现二维欺骗干扰。相比于未调制回波，联合编码调制回波的相参积累结果峰值衰减3.32 dB，且快时间域、慢时间域的旁瓣均有小幅抬升，但从目标检测的角度出发，该调制能够同时对雷达测距和测速进行欺骗，形成距离-多普勒图中任意点的欺骗干扰。而当输入信噪比降低时，干扰所在距离通道和多普勒通道的旁瓣会被噪声掩盖，使干扰更加逼真。另外，如本实验参数，当速度欺骗量结合目标本体径向速度进行设置并优化时，目标将与杂波混叠，能够缩减雷达滤除杂波后的目标能量，进一步避免目标被雷达探测。

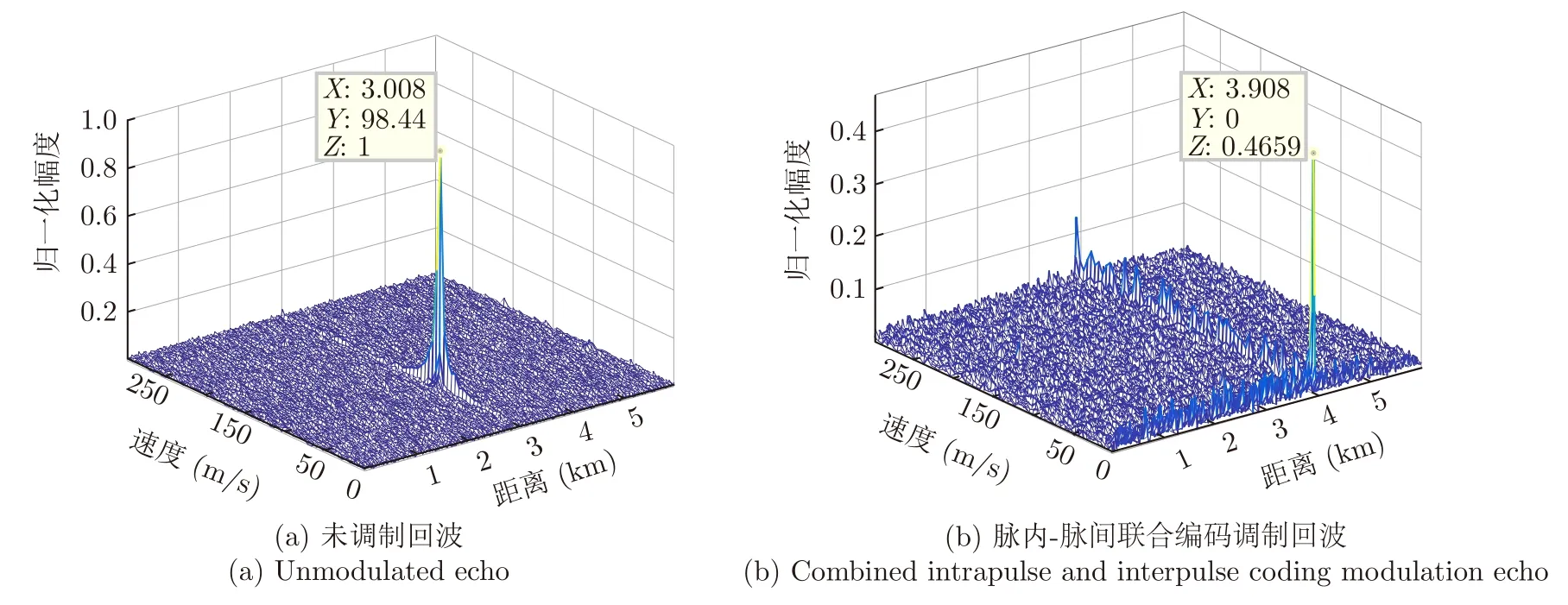
图7 未调制回波与联合编码调制回波距离-多普勒图Fig.7 Range-Doppler diagram of unmodulated echo and jointly coding modulated echo

4.2 仿真实验2 基于相位编码波形的脉内脉间编码优化仿真实验

仿真实验2旨在验证本文所提方法对另一典型波形，即相位编码波形干扰的有效性，参数设置与仿真实验1相同。由于雷达发射波形不影响慢时间域优化过程，仿真实验2仅对快时间域优化结果与脉内-脉间联合编码优化结果进行仿真分析。

图8(a)和图8(b)分别为针对相位编码波形的雷达欺骗干扰结果与算法迭代曲线，仿真结果表明本文所提方法不限制于雷达波形类型，且均能够在较少的迭代后实现较优的水平。而本质上，优化过程是某一时间切片内对雷达回波叠加相位值的求解，而相位编码波形与LFM波形均为恒模波形，其不影响本文所提方法的有效性。

图8 针对相位编码波形的快时间域相位编码优化欺骗干扰Fig.8 Phase coding optimization of deception jamming in fast time domain for phase coded waveform

图9(a)和图9(b)分别为未调制回波与联合编码调制回波的距离-多普勒图。由于慢时间域模型待优化序列与雷达波形无关，仿真实验2沿用仿真实验1中慢时间域优化得到的最优解。仿真结果表明，在雷达发射相位编码波形的情况下，本文所提方法在LFM波形与相位编码波形下实现的欺骗干扰效果大致相同。综上所述，本文所提方法能够适用于脉冲多普勒体制的典型雷达波形。

图9 基于相位编码波形的未调制回波与联合编码调制回波距离-多普勒图Fig.9 Range-Doppler diagram of unmodulated echo and jointly coding modulated echo based on phase coded waveform

4.3 仿真实验3 全局优化仿真实验及对比分析

仿真实验3旨在验证本文所提方法与基于距离多普勒图全局优化方法的优越性。在3.3节所述的全局优化方法中，目标函数由式(14)与式(21)所示对一维序列求取p范数及后续的计算转变为对距离多普勒图中各点形成的二维矩阵求取p范数。

图10为经过二维全局优化编码调制的回波脉冲压缩和相参积累后形成的距离-多普勒图，可以看出该方法能够在设定的干扰距离与干扰速度的位置形成单峰假目标，且该干扰在图中具有均匀的旁瓣。然而，相比于未调制回波的相参积累峰值，基于全局优化形成的干扰峰值衰减9.14 dB。由图7(b)与图10对比可得，本文所提方法脉冲压缩和相参积累后的干噪比提升了5.82 dB。另外，由于基于二维全局优化的模型计算复杂度较高，算法迭代速度与收敛速度均较慢。

图10 基于二维全局优化编码调制回波距离-多普勒图Fig.10 Range-Doppler diagram of coded modulation waveform based on two-dimensional global optimization

图11为快时间域优化模型、慢时间域优化模型以及二维全局优化模型在算法迭代一次中的耗时。由于慢时间域待优化序列长度小于快时间域，其模型的计算复杂度相对较低，因此本文所提方法的迭代耗时与收敛速度可以近似等于快时间域优化迭代耗时。从仿真结果可以看出，本文所提方法的迭代速度相比于二维全局优化模型有数量级优势。

图11 模型迭代耗时对比图Fig.11 Comparison of model iteration time

图12为相同迭代次数下，快时间域优化模型与二次全局优化模型的收敛曲线，并均以受调制回波距离多普勒图作为输入的目标函数进行归一化。由此可见，本文所提方法经过较少的迭代就可以获得较优的结果，且其收敛值远大于二维全局优化模型的上限。另外，根据能量守恒定律，当距离多普勒图中旁瓣水平趋于一致时，干噪比必然会损失。

图12 模型收敛曲线对比图Fig.12 Comparison of model convergence curves

综上所述，本文所提方法无论从优化模型迭代速度和收敛速度都取得了提升。

4.4 仿真实验4 超表面调制间隔对干扰效果影响仿真实验

假设目标径向距离为3000 m，干扰距离为900 m。超表面采用5组相位调控裕度(0°,180°),(0°,120°,240°),(0°,90°,180°,270°),(0°,60°,120°,180°,240°,300°),(0°,45°,90°,135°,180°,225°,270°,315°)离散相位集合，分别对应图13中Nr=2,3,4,6,8，其中Nr表示均匀分布可调相位的数量。超表面调制间隔(时间切片Tc)为100 ns,200 ns,500 ns,800 ns,1 μs,2 μs和4 μs。仿真实验4旨在探究调制间隔大小和相位调控裕度对干扰效果的影响。

首先定义干扰峰值旁瓣比为干扰峰值与旁瓣最大峰值之比，归一化干扰峰值为干扰峰值与未调制回波脉压目标位置峰值之比。如图13(a)所示，干扰峰值旁瓣比随调制间隔的增大而减小，随可调相位数量增加而增大。即快时间脉内相位调控次数越多，干扰越突出、干扰旁瓣水平越低，其与目标相似程度越高。而可调相位数量越多代表受调制回波与参考信号卷积时各点复数矢量相加可调自由度越大，则经过优化的调制序列所形成的干扰越精细化，其干扰效果上限越高。如图13(b)所示，归一化干扰峰值随调制间隔的变化趋势与图13(a)大致相同，该图说明当调制间隔增大时，脉内相位调制对原始信号能量的搬移能力逐渐下降。当调制间隔为1 μs以上时，归一化干扰峰值与原始脉冲在900 m处的脉压幅度处于相同水平，即调制失效。另外，当采用Nr=2即(0°,180°)离散相位调控时，其干扰峰值旁瓣比与归一化干扰峰值均大幅低于Nr取其他值的平均水平，该现象是由于其相位调控始终属于实数，与其他能够形成复数调控的离散相位集相比少了一个调控维度。在本实验中调制间隔对干扰效果的影响是与信号脉宽耦合的，本质上影响调制能力的是信号脉内调制次数。

4.5 仿真实验5 干扰距离对干扰效果影响仿真实验

假设雷达发射LFM波形，目标径向距离为3 km，超表面调制间隔为100 ns。预设干扰距离分别为75 m,150 m,300 m,600 m,900 m,1200 m,1800 m。仿真实验5旨在探究在干扰距离与干扰效果的关系。

如图14(a)和图14(b)所示，当干扰距离增大时，干扰峰值旁瓣比和归一化干扰峰值均呈现下降趋势。超表面相位调制缩减原始目标脉压位置处的能量，并使其在干扰位置聚集，由于LFM波形的距离-多普勒耦合特性，其脉压频谱会形成一定的频移，这会使回波与参考信号匹配滤波时能量缩减，造成干扰位置能量随干扰距离增大而下降的现象。

4.6 仿真实验1—实验5小结

根据上述实验1—实验5相位调制编码策略与参数对比分析可得：(1)干扰距离带来的干扰峰值能量缩减相比于调制间隔的影响更小；(2)可调离散相位集越丰富，调制间隔越小(脉内调制次数越多)，干扰距离越小，其形成的干扰能量越集中，干扰旁瓣水平越低，干扰效果越好。

5 结语

针对超表面对电磁波的调控特性，本文提出了一种基于时域超表面脉内-脉间编码优化的雷达干扰方法。该优化模型分别从快时间域、慢时间域对脉内脉间相位编码进行优化，形成距离-多普勒二维图中任意点欺骗干扰，相比于二维优化的方法松弛了旁瓣性能但大幅提升了计算效率。另外，本文从超表面编码策略的角度分析了调控间隔、可调离散相位集和干扰距离对脉压以及相参处理后干扰效果的影响，为实现欺骗干扰选择最佳策略提供了实验性指导。

在实际情况中可能会出现诸多问题会导致目标能量难以被全部转移，例如：(1)超表面可能会因硬件条件而难以实现稳定且准确的相位差；(2)超表面难以对目标全覆盖；(3)超表面对斜入射波的调制能力不足等。上述问题是超表面设计及其制造工艺亟待解决的问题，而如何在条件受限的情况下通过设计超表面布设方式及调制策略保持干扰的有效性同样值得研究。

利益冲突所有作者均声明不存在利益冲突

Conflict of InterestsThe authors declare that there is no conflict of interests