基于脉间码型捷变波形的距离-多普勒二维干扰重构算法
高宇航 张凯翔 范花玉 刘泉华 刘子豪 王朝旭
①(北京理工大学信息与电子学院雷达技术研究所 北京 100081)
②(卫星导航电子信息技术教育部重点实验室(北京理工大学) 北京 100081)
③(北京理工大学长三角研究院(嘉兴) 嘉兴 314000)
④(北京理工大学重庆创新中心 重庆 401120)
1 引言
随着电子战设备的不断更新,各种电子干扰技术不断出现,对雷达的生存构成了严重的威胁[1-3]。数字射频存储(Digital Radio Frequency Memory,DRFM)技术的出现极大地推动了干扰技术的发展,基于DRFM技术的干扰机通过对雷达发射信号进行截获、存储以及转发等操作,在雷达接收端产生大量与目标高度相似的虚假目标,形成欺骗和压制双重干扰效果[4]。密集假目标干扰是基于DRFM技术产生的典型相参干扰,与目标回波信号具有极高的相似度,会造成真假目标识别困难,极大影响雷达的目标探测能力。本文所讨论的密集假目标干扰是由远距支援干扰机对发射信号进行全脉冲采样并多次转发而形成的,其具有全脉冲复制和脉间相参等特点。通常情况下,远距支援干扰信号滞后目标信号至少一个脉冲重复周期(Pulse Repetition Time,PRT)。
针对该类型密集假目标干扰,常见的解决思路是设计具有良好正交性的波形集。文献[5]基于脉间波形分集理论,通过在不同PRT内发射调频斜率随机扰动的线性调频(Linear Frequency Modulation,LFM)信号来对抗干扰。文献[6,7]通过使不同PRT间发射的脉冲信号相互正交,并在接收端通过匹配滤波来抑制干扰。然而,上述算法只是基于脉间波形分集理论设计波形,其自由度相对有限且波形样式也相对局限。随着优化理论的不断发展,国内外学者引入先进的优化算法来设计具有良好正交性的波形集。文献[8,9]基于优化最小化理论框架设计正交码型捷变波形集。文献[10]利用模因算法强大的全局搜索能力来设计正交离散相位编码波形集。文献[11]结合优化最小化理论和交替方向乘子法来设计具有较好互相关性能的脉间码型捷变波形。在获得一定先验信息的基础上,文献[12-14]通过最小化码型捷变波形间互相关函数中特定区域内的积分能量从而在距离维形成凹口,最终实现干扰抑制。然而,由于波形设计自由度有限导致所设计波形间的正交性能也相对有限,且随着波形数量的增加,算法的运算量也急剧增加。因此,单独依靠波形设计来对抗密集假目标干扰,其抑制效果有限。为了获得更多的优化自由度,部分学者考虑了发射端波形设计与接收端信号处理相结合的思路。文献[15,16]通过同时设计码型捷变波形集与失配滤波器组来提升不同波形失配滤波输出的互相关性能,并利用展宽主瓣和加长失配滤波器处理提高优化自由度。文献[17]提出了一种相干CLEAN方法来抑制干扰,但其计算量较大。综上,可以看出,若只依靠正交波形集,其抑制干扰能力有限;而波形和滤波器联合设计在波形数量较多时,其正交性能也会下降,无法满足强干扰场景中的目标检测需求。
文献[18]提出了交替反演重构方法来实现机载雷达中折叠杂波的分离与抑制。受到该反演重构思路的启发,本文提出一种基于脉间码型捷变波形的距离-多普勒二维干扰重构算法来实现密集假目标干扰的抑制。本文首先建立了密集假目标干扰抑制模型;接着,基于脉间码型捷变波形的距离选通性,在距离-多普勒域中分别重构反演干扰和目标回波信号,进而实现干扰抑制和目标检测;最后,仿真实验表明,本文所提算法能够在强干扰场景中实现目标和干扰的精准重构,具有较强的抗干扰能力,为捷变波形的工程应用提供技术支撑。
2 密集假目标干扰抑制问题建模
本节首先通过图1介绍脉间码型捷变波形的距离选通性,然后基于脉间码型捷变波形的距离选通性构建密集假目标干扰抑制模型。

图1 来自不同距离段的干扰和目标回波以及对应接收滤波器组示意图Fig.1 Diagram of the jamming and target echo from different range intervals and the corresponding receiving filter banks
图1为来自不同距离段的干扰和目标回波以及对应接收滤波器组示意图,以干扰信号滞后目标回波一个PRT为例。为便于表述,此处将回波信号按照PRT划分为具有不同时延的距离段。例如,在图1中,目标位于第0个距离段(即不模糊距离区间),干扰位于第1个距离段(即1次模糊距离区间)。从图1可以看出,从第1个距离段开始的干扰信号会与从第0个距离段开始的目标回波产生重叠,如果雷达发射相同的脉冲信号,则无法区分目标和干扰。如果雷达在脉冲间发射不同的脉冲信号,根据其不重复的性质,可采用不同的接收滤波器组来分离目标回波和干扰信号,该性质称为“距离选通性”。例如,当采用接收滤波器组0处理回波时,接收滤波器组可与目标回波相匹配,而与干扰信号失配。然而当接收滤波器组0与干扰信号失配,其输出能量会散布到整个距离-多普勒平面。该散布能量会严重影响雷达目标探测性能。因此,仅依靠捷变波形的距离选通性来抑制干扰的效果有限,本文通过将捷变波形与信号处理相结合来进一步提高干扰抑制能力。
设雷达在一个相参积累时间内发射M个脉冲,第m个脉冲信号的基带表达式为
其中,Tsub为码片宽度,N为码长,bm,n=exp(jφm(n))为第m个脉冲中第n个码片的相位编码且相位φm(n) 可以在 [0,2π]内任意取值,每一个脉冲调制的相位编码信号均不相同。
假设来自第xT个距离段的真实目标回波信号时延为,其满足
其中,Tr表示PRT,τT表示真实目标回波信号的模糊时延。雷达在第m个PRT内接收到的目标回波信号经过下变频处理后表示为
其中,σT表示目标回波信号的幅度,mod表示取余计算,f0表示载频,τT满足τT=2(RT-mvTTr)/c,RT和vT分别表示目标回波信号的模糊距离和速度,c为光速。
假设干扰机能够截获完整发射脉冲信号,并进行多次转发来形成密集假目标干扰。干扰信号滞后目标回波至少一个PRT,其中第i个假目标干扰的回波时延为满足
设雷达在第m个PRT接收到的干扰信号经过下变频处理后表示为
其中,
不失一般性,在构建优化问题时暂不考虑噪声。设雷达在第m个PRT接收到的回波信号为
其中,ex(m,t)表示第m个PRT中来自第x个距离段的回波信号,X为总距离段数。设第m个PRT中回波信号经过离散采样后表示为e(m,l),信号长度为Le,接收滤波器长度为Lh。用来自第x个距离段回波信号对应的接收滤波器对第m个PRT中的回波信号进行滤波处理,其表达式可以表示为
其中,h(m,l)为第m个脉冲信号对应的接收滤波器,*表示卷积计算,l为回波信号脉冲压缩结果的采样点序号,L为接收滤波输出点数且满足L ≥Le+Lh-1。中上标表示接收滤波器组序号,下标表示回波距离段序号。式(9)对应的频域表达式为
其 中,E(m,l)和H((m-x+M)modM,l)分别为e(m,l)和h((m-x+M)modM,l)的频域表达式。为便于后续推导,将式(10)用矩阵表示,即
若能够恢复出所有的Ex,∀x ∈{0,1,...,X-1},即可实现密集假目标干扰的分离与抑制。因此,本文充分利用脉间码型捷变波形的距离选通性和干扰信号在距离-多普勒平面的分布特性,提出了一种基于脉间码型捷变波形的距离-多普勒二维干扰重构算法。下面对本文所提算法进行具体推导和介绍。
3 基于脉间码型捷变波形的距离-多普勒二维干扰重构算法
3.1 算法推导
本节将对基于脉间码型捷变波形的距离-多普勒二维干扰重构算法进行推导,算法流程图如图2所示。

图2 基于脉间码型捷变波形的距离-多普勒二维干扰重构算法流程图Fig.2 Flowchart of the range-Doppler two-dimensional jamming reconstruction algorithm based on interpulse code agile waveform
本文所提算法首先对回波信号进行分距离段相参处理,其中回波分距离段相参处理指回波信号经过来自不同距离段回波信号对应的接收滤波器组处理后进行慢时间加窗多普勒处理。需要注意的是,由于脉间码型捷变波形在各脉冲间调制了不同形式的相位编码信号,因此各脉冲匹配滤波输出的距离旁瓣结构不同,该现象被称为距离旁瓣调制(Range Sidelobe Modulation,RSM)效应[19,20]。RSM效应会导致脉间码型捷变波形经过脉冲多普勒(Pulse Doppler,PD)处理后能量沿多普勒维散布,严重影响强干扰场景下雷达对目标的检测能力。文献[21]针对RSM效应,设计了联合失配滤波器组使各脉冲失配滤波输出结果的距离旁瓣接近一致,可有效抑制捷变脉冲串信号的RSM效应。因此,本文采用文献[21]所设计的联合失配滤波器组抑制脉间码型捷变波形带来的RSM效应。
针对第m个发射脉冲信号,设其对应失配滤波器离散形式为hmmf(m,l)。则第m个PRT接收的雷达回波在第x个距离段对应的失配滤波器组处理下,失配滤波输出结果可表示为
对式(14)中两边的序列分别补零至长度L点并沿快时间维作L点离散傅里叶变换后,其频域表达式为
为便于后续推导,式(15)改写成矩阵形式可表示为
当x>0时,有
其中,diag{w}表示以向量w=[w(0)w(1) ...w(M-1)]T为对角元素的对角矩阵,向量w中的元素为加窗函数的权值,(·)T表示转置操作。本文所提算法的核心是在多普勒维尽可能地分离来自其他距离段回波折叠到第x个距离段的能量。因此,为了使来自第x个距离段回波的相参输出能量在多普勒维尽可能地聚集,本文采用具有低旁瓣电平特性的加窗函数,如Chebyshev窗[22]等。
由于脉间码型捷变波形的距离选通性有限且回波信号包含来自多个距离段的回波信号,当来自其他距离段的回波信号通过失配滤波器组,其对应的输出能量仍然较高且散布在整个距离-多普勒平面,严重影响雷达目标探测能力。
为了解决该问题,本文设置滤波矩阵提取来自第x个距离段回波信号的相参积累能量。针对来自第x个距离段回波信号的相参处理结果,设置滤波矩阵为
设第k次迭代后来自第x个距离段干扰信号所对应频域矩阵为则在第k+1次迭代时,迭代算法的递推公式可表示为
最终,结合上述推导过程,来自第x个距离段回波信号的相参处理结果(即距离-多普勒成像结果)可以表示为
在完成回波信号中所有干扰信号的重构后,可执行目标检测流程。目标检测可以采用常规的恒虚警检测(Constant False-Alarm Rate,CFAR)。当检测到新的目标后,更新目标回波所在距离段的滤波矩阵,并重新执行迭代重构过程,从而实现更加精确的干扰和目标回波反演重构,其中目标回波对应的滤波矩阵设计思路与干扰信号对应的滤波矩阵设计思路保持一致。
综上,已完成对基于脉间码型捷变波形的距离-多普勒二维干扰重构算法的全部推导,其具体算法流程总结为算法1。

算法1 基于脉间码型捷变波形的距离-多普勒二维干扰重构算法Alg.1 Range-Doppler two-dimensional jamming reconstruction algorithm based on interpulse code agile waveform
3.2 计算复杂度分析
4 仿真实验与结果分析
4.1 抗干扰效果分析
本节构造典型密集假目标干扰场景,通过仿真实验来验证所提算法的有效性。假设场景中目标位于第0个距离段,其距离为12 km,速度为50 m/s;场景中存在2部远距支援干扰机,干扰机1在第1个距离段[85.8,91.8] km范围内随机产生40个假目标,其假目标速度分别为40 m/s和50 m/s;干扰机2在第2个距离段[162.6,168.6] km范围内随机产生20个假目标,其假目标速度为60 m/s;若采用常规LFM信号,假目标干扰的视在距离均在[9,15] km范围内。此外,设置信干比(Signal to Jamming Ratio,SJR)为-40 dB,信噪比(Signal to Noise Ratio,SNR)为-5 dB,窗函数采用Chebyshev窗,其主瓣宽度对应的速度区间宽度为30 m/s。波形参数如表2所示,其中发射脉冲串信号在一个相参积累时间内发射128个脉冲,每个脉冲调制不同的连续相位编码信号,相应的码长为128,每个相位编码信号可采用文献[23]所提的方法来进行设计。针对发射脉冲串信号,采用文献[21]所提的联合失配滤波器组设计方法来设计对应的失配滤波器组。

表1 交替反演重构干扰/目标的计算复杂度Tab.1 Computational complexity of alternate inversion reconstructed jamming/target

表2 波形参数Tab.2 Waveform parameters
图3为LFM与脉间码型捷变波形回波在密集假目标干扰场景下的分距离段相参处理结果。由图3(a)可知,由于LFM信号在脉冲间参数保持不变,所以干扰信号能够在目标所在距离段形成欺骗和压制双重干扰效果。由图3(b)可知,由于脉间码型捷变波形在脉间捷变,干扰信号折叠到目标所在距离段的干扰能量受到部分抑制,但是干扰信号与目标所在距离段对应的接收滤波器组失配导致干扰折叠能量沿多普勒维发散。当干扰折叠能量较强时,干扰信号沿多普勒维发散的能量也会淹没目标从而无法实现目标检测。该仿真也验证了脉间码型捷变波形在强干扰场景中的局限性。同时,由图3(b)可得,干扰信号在各自所在距离段具备能量聚集的特性,即可以看出干扰信号位于第1个距离段和第2个距离段。根据在3.1节定义的干扰信号通带范围确定准则,可以得到来自第1个和第2个距离段干扰信号所对应滤波矩阵的多普勒通带范围分为[25,65] m/s和[45,75] m/s。

图3 LFM与脉间码型捷变波形回波分距离段相参处理结果对比Fig.3 Comparison of the coherent processing results of the different range intervals between LFM and interpulse code agile waveform echoes
由于文献[21]设计的失配滤波器组具有多普勒敏感性,需对回波信号进行速度补偿来减弱脉内多普勒频移对失配滤波输出结果的影响。考虑到密集假目标干扰为了对目标形成欺骗和压制双重干扰效果,干扰信号所产生假目标的速度与真实目标速度不会相差太大。因此,考虑选取回波信号分距离段相参处理结果的最大值所对应的速度作为补偿速度,来减弱脉内多普勒频移带来的影响。
经过速度补偿后,采用基于脉间码型捷变波形的距离-多普勒二维干扰重构算法进行干扰抑制。图4给出了该算法在不同迭代次数下的分距离段相参处理结果。由图4(a)和图4(b)可得,当迭代次数为2次时,目标被来自其他距离段折叠过来的干扰能量所覆盖,但是与图3(b)相比,目标所在距离段中的折叠干扰能量已经极大减少;由图4(c)和图4(d)可得,经过约10次迭代后,目标可以完全显露出来,且目标所在区域基底与噪声基底基本一致,说明了所提算法实现了干扰信号的有效重构。此时,干扰抑制后的信干噪比(Signal-to-Jamming-plus-Noise Ratio,SJNR)约为31.21 dB。通过对图4(d)展示的分距离段相参处理结果进行目标检测,其中检测到的目标在图4(d)中用红色椭圆标出。但是由于重构过程中未考虑重构目标,在算法迭代滤波过程中,目标能量会有一定程度的失真。因此,考虑设计目标所在距离段的滤波矩阵并重新执行迭代重构来实现干扰和目标的精确重构。由图4(c)和图4(d)可知,目标所在距离段的滤波矩阵对应的通带范围为[35,65] m/s。更新目标所在距离段的滤波矩阵,并重新执行迭代反演重构过程,可得到图5所示的结果,其干扰抑制后的SJNR为32.48 dB。可以看出,通过将目标加入迭代反演重构过程中,目标能够被更加精准地重构出来,从而有效减小目标在迭代反演过程中的失真。

图4 不同迭代次数下的分距离段相参处理结果Fig.4 Coherent processing results of the different range intervals under different iterations
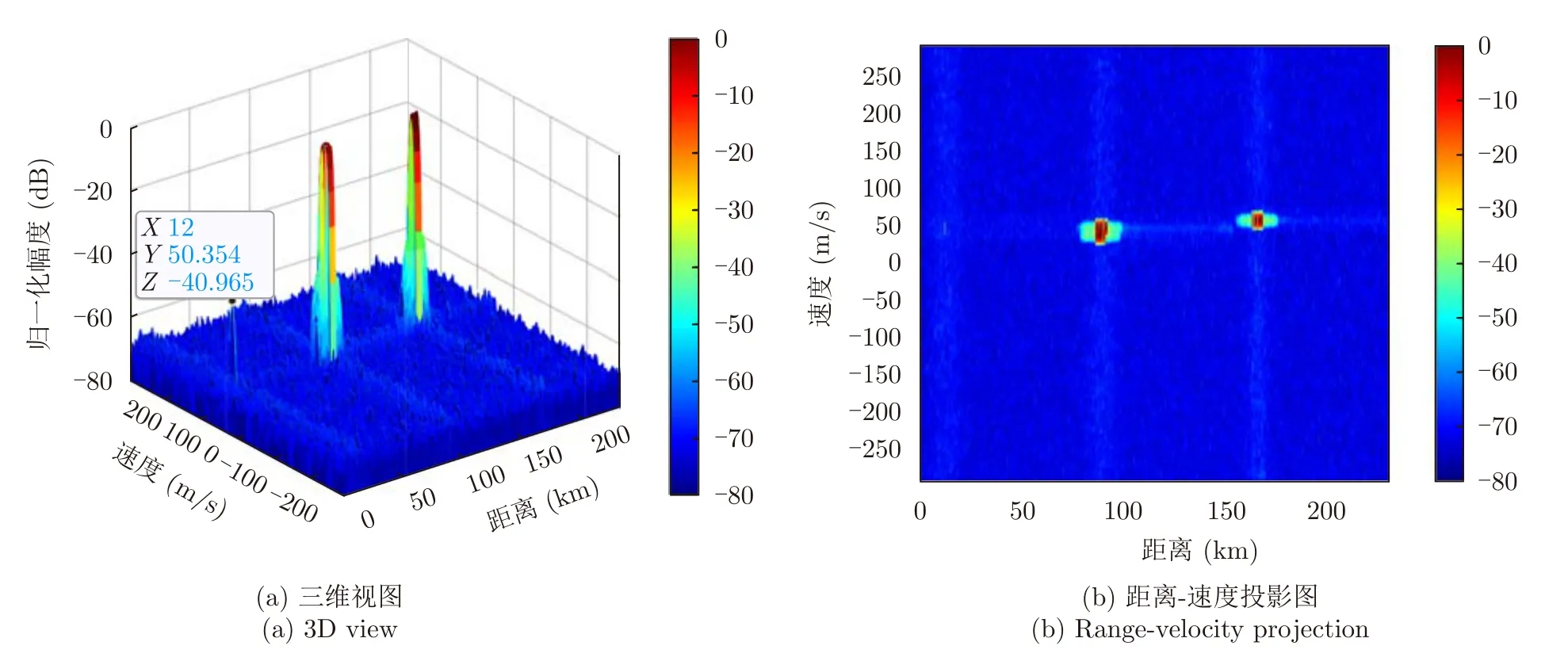
图5 干扰与目标的反演重构结果Fig.5 Inversion reconstruction results of jamming and target
4.2 算法性能对比
本节对所提算法的干扰抑制性能进行分析,并选取文献[17]所提的CLEAN算法进行对比。首先,针对如图3(b)所示的脉间码型捷变波形回波,本文给出了其经过CLEAN算法处理后的干扰抑制结果,如图6所示。将图5与图6的结果进行对比,可以看出,CLEAN算法虽然能够抑制目标所在距离段的大部分干扰能量,但是还剩余部分干扰能量,此时,干扰抑制后的SJNR为26.83 dB。与CLEAN算法相比,本文所提方法能够更加精准地分离出目标所在距离段的干扰能量,获得更好的干扰抑制效果。此外,对所提算法和CLEAN算法各开展10组仿真,并记录每组仿真的运行时间,其平均运行时间如表3所示。由表3可得,与CLEAN算法相比,所提算法具有较高的运行效率。

表3 运行时间对比(s)Tab.3 Comparison of running time (s)

图6 CLEAN算法处理后的干扰抑制结果Fig.6 Jamming suppression results after CLEAN algorithm processing
图7给出了所提算法和CLEAN算法在不同SNR条件下干扰抑制后的SJNR随SJR的变化曲线,其中实线曲线为本文所提算法的变化曲线,虚线曲线为CLEAN算法的变化曲线。由图7可得,当SJR较高同时SNR较低时,所提算法干扰抑制后的SJNR与CLEAN算法基本一致,甚至会出现CLEAN算法干扰抑制后的SJNR略高一点。这是因为当干扰信号能量较小时,经过两种算法抑制后,都可将目标所在距离段的干扰能量抑制到噪底以下,但是所提算法设计的滤波矩阵在提取干扰/目标能量的同时也会提取一部分噪声能量,由于噪声是非相参的,所以在迭代过程中该部分噪声能量无法进行重构,进而导致在干扰对消过程中该部分噪声能量出现失真,最终造成距离-多普勒平面基底的略微抬升。因此,该现象导致了CLEAN算法在低SNR和高SJR条件下,干扰抑制后的SJNR略高于所提算法干扰抑制后的SJNR。当SJR较低时,所提算法干扰抑制后的SJNR远高于CLEAN算法输出的SJNR。此外,随着SJR的不断减小,所提算法干扰抑制后的SJNR逐渐下降。该现象产生的原因是联合失配滤波器组具有多普勒敏感性。虽然本文在4.1节对回波进行速度补偿来降低脉内多普勒频移带来的影响,但由于无法精确补偿脉内多普勒频移,联合失配滤波器组抑制RSM效应的性能会出现下降,导致干扰信号经过PD处理后能量会沿多普勒维散布;在每一次迭代过程中,滤波矩阵无法较为完整地提取干扰/目标信号的能量,使得所提算法对干扰/目标的重构精度下降,最终导致干扰抑制后的距离-多普勒平面基底抬升。SJR越小,干扰能量越强,其沿多普勒维散布能量越强,最终造成干扰抑制后的SJNR越小。

图7 不同SNR条件下SJNR随SJR的变化曲线(实线为本文算法,虚线为CLEAN算法)Fig.7 SJNR curve with SJR value under different SNR conditions (the solid lines represent the proposed algorithm,and the dashed lines represent the CLEAN algorithm)
4.3 算法鲁棒性分析
4.3.1 干扰信号失真对算法性能影响
本文假设干扰机能够完整截获整个雷达发射脉冲并且能够实现无失真转发。然而在实际中,干扰机转发截获信号时会存在部分失真。因此,本节分析当干扰机转发截获信号存在失真的情况,通过对转发的每个脉冲调制一个 [-a,a]内随机产生的相位来模拟干扰机失真,同一干扰机产生的每个假目标其调制的相位扰动是相同的。设a={0°,0.2°,0.4°,0.6°,0.8°,1.0°,1.2°,1.4°,1.6°,1.8°,2.0°},SJR分别为-20 dB,-30 dB和-40 dB,其他仿真参数与4.1节保持一致。图8给出了干扰抑制后的SJNR随a值的变化曲线。由图8可知,当SJR固定时,干扰抑制后的SJNR随着a值的增大而减小。这是因为重构目标和干扰的准确度随着a值的增大而下降;当a值固定时,干扰抑制后的SJNR随SJR的减小而减小。这是因为SJR越小,经过交替反演重构后的目标所在距离段中剩余干扰能量越大,导致干扰抑制后的SJNR越小。此外,当a=2°时,干扰抑制后的SJNR明显下降,最多下降了约15 dB。综上可得,本文所提算法对干扰机的转发失真较为敏感。
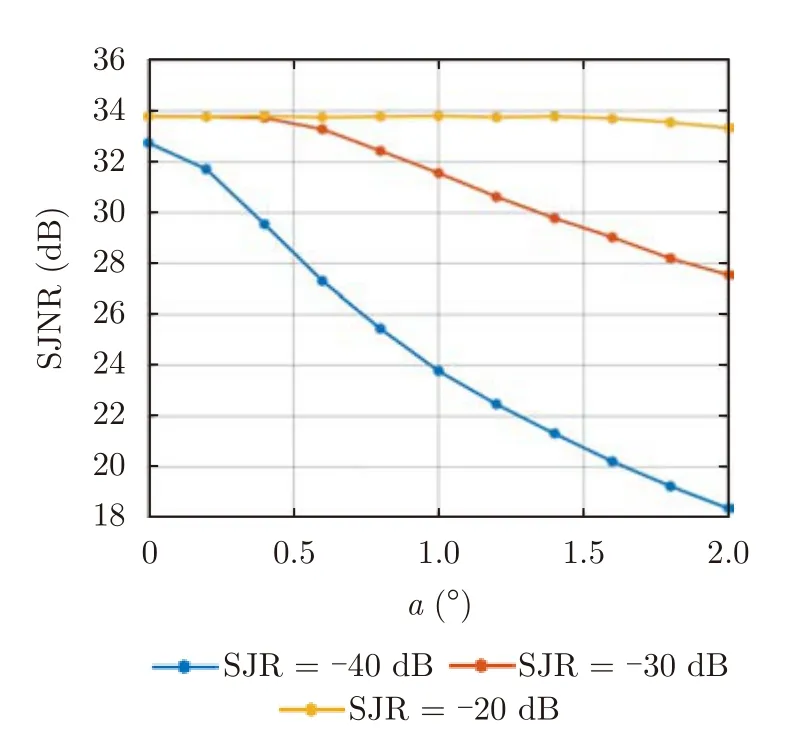
图8 SJNR随a值的变化曲线Fig.8 SJNR curve with a value
4.3.2 干扰速度对算法性能影响
在4.1节中,本文在对回波处理之前进行了速度补偿来减轻脉内多普勒频移的影响;因此,本节分析当速度补偿存在误差时,不同干扰速度对算法性能的影响。为便于分析,假设场景中存在1部干扰机,其在第1个距离段[85.8,91.8] km范围内随机产生40个假目标,其中20个假目标速度为50 m/s,剩余20个假目标速度为vJ,vJ的取值分别为{50,60,70,80,90,100,110,120,130} m/s;SJR分别为-20 dB,-30 dB和-40 dB,其他仿真参数与4.1节保持一致,选取回波信号分距离段相参处理结果的最大值所对应的速度作为补偿速度。图9给出了干扰抑制后的SJNR随vJ值的变化曲线。由图9可得,当SJR固定时,干扰抑制后的SJNR随vJ值的增大而减小。这是因为vJ越大,脉内多普勒频移越大,导致联合失配滤波器组抑制RSM效应的性能越差,进而使得所提算法对干扰/目标的重构精度下降,最终造成干扰抑制后的距离-多普勒平面基底抬升。当vJ值固定时,SJR越小,干扰抑制后的SJNR越小。这是因为SJR越小,干扰能量越强,其沿多普勒维散布能量越强,导致干扰抑制后输出的距离-多普勒平面基底越高。
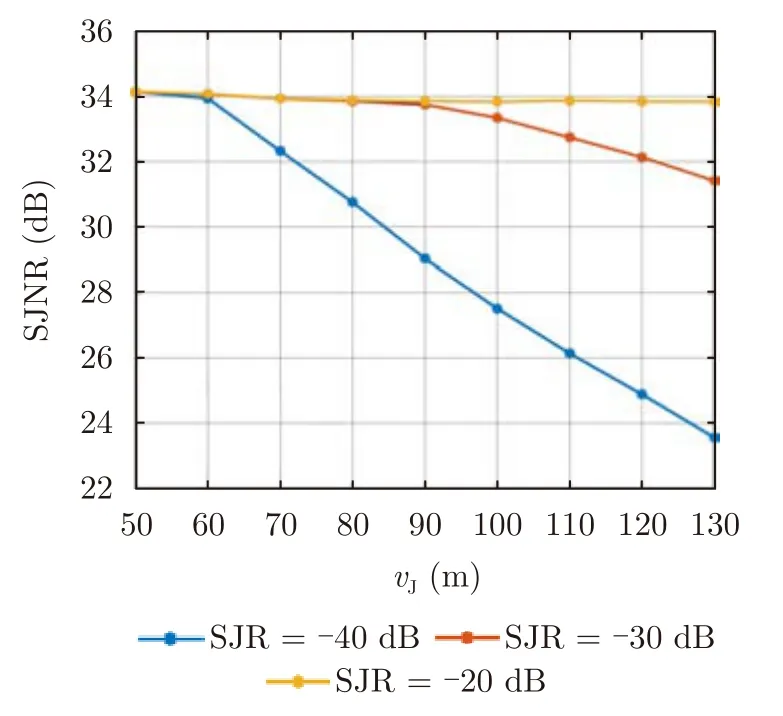
图9 SJNR随 vJ 的变化曲线Fig.9 SJNR curve with vJ value
5 结语
针对远距支援干扰场景中的密集假目标干扰,本文根据脉间码型捷变波形的距离选通性,提出了一种距离-多普勒二维干扰重构算法。该算法利用干扰和目标回波在不同距离-多普勒平面上的能量分布特性来反演重构干扰和目标,最终实现干扰能量的剔除和目标的检测。仿真实验表明,与现有算法相比,本文所提算法能够更高效地实现密集假目标干扰抑制。需要指出的是,本文所提算法假设干扰机具有良好的相参性,并且干扰速度与补偿速度之间的差异较小。当干扰信号与发射信号的一致性较差或者干扰速度与补偿速度相差较大的情况下,本文所提算法的抗干扰能力将减弱。
利益冲突所有作者均声明不存在利益冲突
Conflict of InterestsThe authors declare that there is no conflict of interests

