基于改进A星算法的无人车路径规划研究
缪殷俊 施卫

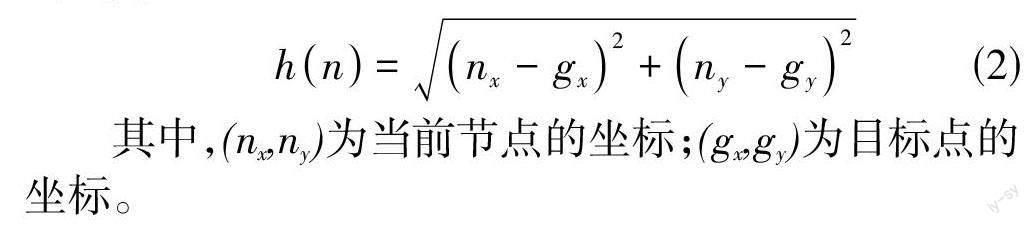
关键词:无人车避障路径规划;改进A星算法;关键节点优化
中图分类号:TP301 文献标识码:A
文章编号:1009-3044(2024)03-0004-04
0 引言
路径规划是无人车智能驾驶技术中非常核心的一门技术[1],无人车需要按照预定的地图到达指定目的地,在相对应的地图上进行路径规划,需要相应的路径规划算法,而常用的全局路径规划算法有很多种,比如:Dijkstra算法[2]、A星算法[3]、蚁群算法[4]等。其中,A星算法是一种较经典启发式搜索算法,被广泛应用在全局路径规划中[5]。传统的A星寻路算法是用于解决静态环境中最优路径的直接搜索算法,其广泛应用于室内无人车路徑搜索,是在Dijkstra算法的基础上结合了广度优先搜索算法(BFS)[6]。因此,为了能使无人车在栅格化的电子地图中规划出较优的路径,以安全高效的速度抵达目标点,本文提出了一种基于优化改进A星算法的路径规划算法,具体的,优化改进的过程如下:首先,对传统的A星算法进行改进,对A星算法的评价函数进行改进,优化启发函数h(n)加入权重系数,使得搜索效率提高,搜索邻域优化,优化搜索方向将多余的搜索方向剔除以减少遍历节点数目,提高搜索效率,其次,对关键节点进行优化处理,删除多余节点,减少路径上的冗余节点和转折点,提高算法的运行效率,提高路径的平滑度,然后,对栅格地图进行优化,将地图中的障碍物进行膨胀处理,提高安全性能,并将优化后的算法与原先的算法进行实际分析比较,最终实现无人车的路径规划。
1 优化A星算法
1.1 环境地图构建
在对无人车进行全局路径规划时,首先需要建立一个可以完整表达地图环境信息的环境地图,然后在构建好的环境地图上规划出一条满足要求的最优路径。而在常用环境地图构建的方法中,一般采用栅格地图,因为栅格地图具有简单有效、易于实现的特点,而且可以通过改变栅格大小来改变环境的分辨率,也可以展示出各种不同形状,大小的障碍物。
本文采用栅格法进行环境地图的构建,构建的栅格地图如图1所示。
如图1所示,构建一个大小为10×10的栅格地图,在图中标注出无人车的起始点s,目标点g。
1.2 传统A星算法
传统的A星算法基于代价函数在电子地图中规划全局路径,是最有效的求解全局路径的启发式搜索方法,是贪心算法和Dijkstra算法的结合[7],其基本的表达式为:
f (n) = g (n) + h (n) (1)
式中:f(n)表示为当前节点的总代价,g(n)当前节点与起点的实际代价,h(n)为当前节点距离目标节点的预估代价。
启发函数h(n)的选择对于A星算法的搜索效率有着重要的影响。通常启发函数h(n)的选择有曼哈顿距离、欧几里得距离、切比雪夫距离3种。
欧几里得距离是这3种距离当中运算量最大的,但是求得的路径质量是最好的,所以本文采用欧几里得距离来计算节点的估计代价h(n),欧几里得距离的公式为:
传统A星算法的基本步骤如下:
第1步:建立open列表与close列表,将起点放入open列表中,close列表为空。
第2步:遍历起点周围的节点,计算出他们的评价函数f,将它们放入open列表中,将open列表中评价函数f最小的节点从open列表中移除,并将其加入close 列表中。如果open列表中没有节点,则寻路失败;如果当前节点为终点,则寻路结束,并将终点的前置节点设置为当前节点,然后返回由当前节点到起点的路径。
第3步:遍历当前节点的周围节点。如果邻接点在close列表中,则不作处理;若有邻接点为障碍物,则不予考虑;如果邻接点不在open列表中,则更新其评价函数中的g(n),h(n),并计算出评价函数f(n),再将其放入open列表中;如果邻接点已经在open列表中,则比较从当前节点到这个邻接点的实际损耗g(n)是否比这个点原来的实际损耗g(n)更优,如果不更优,则不作处理;如果更优,则将邻接点的实际损耗g(n)更新为更优值,并将邻接点现在的评价函数f(n)取代之前的f(n)。
第4步:回到第3步,继续处理当前节点周围的下一个邻接点。
第5步:重复以上步骤,直至扩展到目标节点或open列表为空,若非空,则回到第2步继续循环,最终将close列表中的节点依次连接,生成路径。
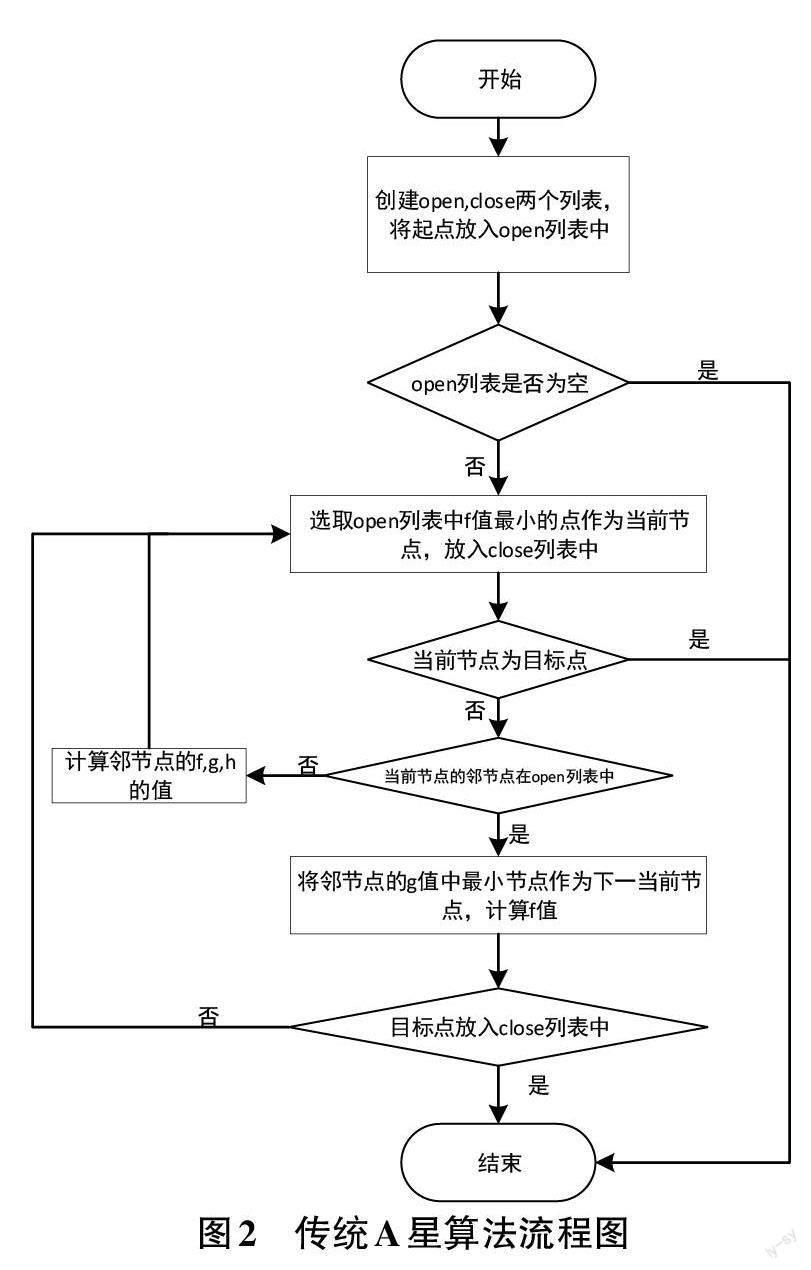
传统A*算法流程图如图2所示。
1.3 优化启发函数
传统A星算法存在一些问题,比如:冗余节点过多,存在重复访问不必要节点的情况;路径不平滑问题,会产生较多的转折点,降低了路径的顺滑度;搜索范围较大,出现不必要的搜索范围,降低搜索速度;最终规划出的路线不太符合实际用途,与障碍物距离较近,易发生事故风险。因此,本文采用动态权重的方法,通过动态调整启发函数的权重系数来提高搜索效率,提高算法的地图适应性。
h(n)的选取是规划最优路径的关键[8],若h(n)小于g(n),虽然此时的路径是最小代价路径,但是搜索节点会变多,范围会变大,搜索时间变长,效率低下;若h(n) 大于g(n),则搜索的速度会大幅提升,但此时的路径可能不是最优解;因此考虑在初期增加h(n)值,提高搜索速度;当当前节点的位置接近终点时,实际代价值g(n) 与估计代价值h(n)大小接近,此时的执行效率处在最优的情况;当障碍物数量占比较多时,动态减小搜索速度,确保寻得路径的精度,提高安全性能,通过减少h(n)的权重系数来处理。当障碍物占比较少时,应加快搜索速度,如果按照传统A星算法的h(n)寻找最优路径,会导致搜索节点过多,搜索效率降低,此时加大h(n)的权重系数。因此,改进后的启发函数如式(3) 所示:
式中,P 表示起始点与目标点之间的障碍率,d 为此时所在节点n 距离目标点的长度;D 为起始点距离目标点的距离长度。
图3为采用传统A星算法规划的路径和遍历的节点。
1.4 搜索邻域优化
传统的A星算法在进行相应的节点搜索时会扩展以当前节点为中心的相邻8个栅格[9],如图4所示,节点1~8为当前可探索的所有节点方向,因为在实际的无人车运动时,目标点的方位已经确定了,在知晓目标点方位的情况下,如果还对八个方向都进行相应的节点搜索就会花费更多时间,遍历更多的节点,导致搜索效率的下降,在实际的搜索过程当中,有些方向是根本运用不到的,需要将这些多余的方向剔除掉。根据上述问题,本文提出一种根据目标点的方位,在搜索过程中只使用其中的5个方向的方法,假设目标点与当前节点的连线与节点2的指示方向的夹角度数为θ,则保留与舍弃方向的规则如表1所示。
1.5 优化关键节点
由图3可知,本文的传统的A星算法在路径规划的过程中会产生有较多的转折点,转折点越多,则越不利于无人车的运动,无人车的工作效率就会降低,并且容易出现与障碍物发生碰撞、刮蹭的行为。针对上述的问题,本文将对关键节点进行优化提取,将路径规划过程中的拐点数目减少,优化关键节点的相关步骤如下:
第1步:在算法遍历节点的过程中会得到相应的节点,节点数目为n1,n2,…,nz个,设立一个集合U用于存放全部遍历的节点,集合V用于存放关键节点。将得到的全部节点都存入到节点集U{ni,1≤i≤z},其中n1表示路径的起点,nz表示路径的终点。将关键节点集V进行相应的初始化,以满足后面的应用需求,关键节点集V中存入起点n1和终点nz。
第2步:将n1依次与n2,n3,n4,…,nm连接,判断连接之后所产生的线路是否出现穿过障碍物的情况,当n1nm是第一条穿过障碍物的直线,则nm的前一个节点nm-1作为路径优化过程中的关键节点,将节点nm-1添加到关键节点集V中,并且将n1与nm-1之间的节点判定为冗余节点。随后以同样的方式进行判断,即从nm开始依次连接后面的节点,并判断是否穿过障碍物,如果穿过就按照之前的处理步骤,将穿过障碍物的点的前一个节点设置为关键节点,并存入关键节点集V 中,一直到连接到终点nz结束。
第3步:步骤二中得到了路径中的所有关键节点,将这些关键节点依次连接起来,最终所得到的路径即为提取关键节点后的路径。
图5为优化示例图:
1.6 障碍物膨胀处理
通过观察图3的传统A星算法路径规划图可以发现,在经过一些障碍物时,传统A星算法是贴着障碍物的边缘走的,这显然不符合无人车实际运动要求,因为无人车本身存在自身宽度,在路径规划过程中,按照一般路径规划算法所规划出的路径有时会出现无人车与障碍物发生碰撞、刮蹭的情况,所以需要先对障碍物进行膨胀处理,膨胀范围为无人车的车身宽度d。在路径规划完之后再将障碍物缩小成原来的大小,从而很好地避免在无人车运动拐弯的时候与障碍物发生碰撞、刮蹭的情况,图6为障碍物膨胀处理示意图。
2 仿真实验与分析
2.1 改进A 星算法仿真分析
仿真实验在MATLAB R2022B环境下进行,为验证改进后算法的有效性以及适应性。分别采用传统A星算法与优化改进后的A星算法进行路径规划实验分析,为了保证有较好的对比效果,改进A星算法的仿真结果如图7所示,传统A星算法与改进优化后的A星算法的对比图,如图8所示,传统A星算法与改进优化后的A星算法的数据性能比较如表2所示。
由表2中的实验数据可知,经过改进优化后的A 星算法与传统A星算法的路径相比要更优,算法的探索规划时间更短,速度更快,相比于传统的A星算法的规划时间结果,改进优化后的A星算法的规划时间减少了28.25%,遍历节点总数减少了27.12%,路径长度从14.188 6缩短到了14.071 1,优化了0.83%;拐点数从5次变为了3次,优化了40%。
因此,本文的改进A星算法可以提高传统A星算法的效率。
3 结束语
本文主要针对传统A星算法的路径规划过程中出现的一些问题进行优化处理,比如:拐点过多、冗余节点多、容易发生碰撞、效率低,路径非最优解。本文对传统的A星算法进行改进。在全局路径规划方面,首先,通过对h(n)进行改进加入权重系数,然后,对搜索邻域进行优化,剔除多余的方向,其次,使用关键点提取策略去除冗余节点,最后,对路径过程中的障碍物进行膨胀处理以避免无人车在路径规划中过度靠近障碍物产生碰撞风险。通过对传统A星算法与优化改进后的A星算法进行仿真实验分析,并对实验数据进行相应的比较,验证出本文改进优化后的A星算法的性能相比于传统的A星算法要更好,路径搜索的效率更高。但是只做全局路径规划还是不够的,即使应用在无人车上也不能很好地保障实际运行过程中的安全、高效。今后笔者将考虑局部路径规划的问题,对局部路径规划进行相应的算法优化,将优化后的局部路径规划算法与优化改進后的A星算法进行融合,并进行相应的实验分析,以进一步验证该优化融合之后的算法在实际场景中进行路径规划时的有效性。
【通联编辑:唐一东】

