考虑变速器结构影响的曲轴计算分析
陈 超 郑晓丰 赵胜权 卢晶晶
(宁波市鄞州德来特技术有限公司 浙江 宁波 315100)
引言
曲轴在运动过程中受到气体作用力、往复运动和旋转运动产生的惯性力及转矩和弯矩的影响,会产生疲劳应力和轴颈油膜压力。当疲劳应力及油膜压力过大时,会出现零件失效现象[1]。
本文结合传动链的零部件结构和布置形式,对新设计的曲轴进行了有限元仿真计算分析。考虑到曲轴后端双质量飞轮、离合器、变速器主轴、变速器壳体、油底壳等零部件刚度、转动惯量及弯矩对仿真计算分析结果产生影响,在建立曲轴多体动力学模型时,对模型进行了缩减。
1 模型建立和边界条件设置
1.1 多体动力学模型的建立
建立曲轴多体动力学模型时,曲轴通过自带autoshaft 功能进行缩减,双质量飞轮采用专用的Dual_Mass_Flywheel 模块,缸体、油底壳、变速器壳体等在建立有限元网格模型时进行缩减。
曲轴多体动力学模型如图1 所示。

图1 曲轴多体动力学模型
1.2 有限元网格模型缩减
因原始网格模型包含的零件较多,应用模态缩减分析理论[2],采取质量-刚度矩阵等效处理方式进行模型缩减,可大大简化分析时间。考虑到模型连接特征及绘制网格的时间成本,对油底壳进行质心简化,曲轴与周边零件采用MPC(多点耦合)连接,缸套和轴瓦采用六面体网格绘制,变速器壳体、缸体采用大网格绘制。缸体上表面约束自由度123,缸套保留节点123,轴瓦径向内圈保留节点23,第3 主轴瓦两止推端面保留节点1。
有限元网格缩减模型如图2 所示。

图2 有限元网格缩减模型
1.3 材料属性
表1 是曲轴仿真计算分析所用材料属性。

表1 曲轴仿真计算分析所用材料属性
1.4 边界条件
1.4.1 机油温度、轴瓦参数边界条件
机油牌号为0W-20,机油温度为140 ℃。
轴瓦参数见表2。

表2 轴瓦参数
1.4.2 载荷边界条件
载荷边界条件为气体压力,最大爆发压力为11MPa。见图3。
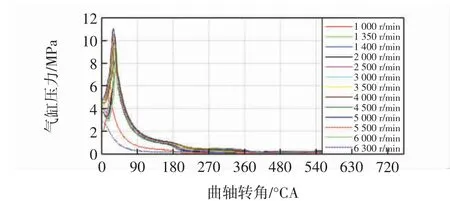
图3 载荷边界条件
2 计算分析结果
2.1 EHD 分析结果
本文通过EHD(Elasto-Hydro Dynamic,弹性流体动力学)[3]计算来评价轴瓦的油膜总压力、表面粗糙接触压力、热负荷、摩擦功率损失、机油温度升高程度。评价指标见表3。表3 中,APFL(Asperity Friction Power Loss)为粗糙摩擦功率损失,TFLP(Total Friction Power Loss)为总摩擦功率损失。

表3 评价指标
本文对发动机转速为5 500r/min 时第5 主轴瓦进行EHD 计算。
油膜总压力分布计算结果如图4 所示。

图4 油膜总压力分布
表面粗糙接触压力计算结果如图5 所示。

图5 表面粗糙接触压力
轴瓦平均热负荷计算结果如图6 所示。

图6 轴瓦平均热负荷
轴瓦摩擦功率损失计算结果如图7 所示。图7中,Hydrodynamic Friction Power Loss 为流体动力摩擦损失。

图7 轴瓦摩擦功率损失
轴瓦机油温度升高程度计算结果见表4。

表4 轴瓦机油温度升高程度
从图4~图7 以及表4 可以得出,计算结果满足指标要求。
2.2 曲轴疲劳因子
曲轴在弯曲、扭转载荷反复作用下,容易在轴颈圆角处产生应力集中,进而引起曲轴疲劳破坏[4]。本文中,第4 缸连杆轴颈位于飞轮端附近,更容易产生疲劳破坏。。
在各转速的爆发压力作用下,曲轴各轴颈圆角处疲劳因子分布如图8 所示。图8 中,web 表示曲柄臂块。

图8 在各转速的爆发压力作用下曲轴轴颈圆角处疲劳因子分布
从图8 可以看出,在各转速的爆发压力作用下,曲轴各轴颈圆角处疲劳因子均大于1.5,满足疲劳因子大于1.1 的设计要求。
在转速为4 500 r/min 的爆发压力作用下,第4缸连杆轴颈圆角处疲劳因子分布如图9 所示。

图9 第4 缸连杆轴颈圆角处疲劳因子分布
从图9 可以看出,第4 缸连杆轴颈圆角处最小疲劳因子为1.51@4 500 r/min,满足疲劳因子大于1.1 的设计要求。
3 结论
对某发动机曲轴进行了仿真计算分析,得到如下结论:
1)对发动机转速为5 500 r/min 时第5 主轴瓦进行了EHD 计算。结果表明,第5 主轴瓦的油膜总压力、表面粗糙接触压力、热负荷、摩擦功率损失、机油温度升高等均满足评价指标要求。
2)在各转速的爆发压力作用下,曲轴各轴颈圆角处的疲劳因子均大于1.5,其中第4 缸连杆轴颈圆角处最小疲劳因子为1.51@4 500 r/min,满足疲劳因子大于1.1 的设计要求。

