基于M odelica模型的供热系统动态热特性研究

王永刚，刘智勇 ，管 铮，朱 越，冯 宁

（1.兰州交通大学环境与市政工程学院，甘肃 兰州 730000；2.华北理工大学建筑工程学院，河北 唐山 063000）

供热管网动态热特性的研究不仅是集中供热系统运行策略优化的重要研究内容，同时也是可再生能源多源并网技术的关键节点，对于优化集中供热运行调节方案具有重要意义。它不仅包括对管网末端温度响应延迟性的研究，还包括对系统热惯性的研究和利用。但与供热管网稳态热特性建模相比，动态建模需要对集中供热管网建立科学且准确的热工水力物理模型，并能在负荷频繁波动的运行情况下，计算出供热管网中各管段介质的流动状态，且支持利用管网仿真运行参数对管网进行热损、蓄能分析[1]。这个问题的解决不仅需要高精度的、贴近实际物理系统的、动态的供热管网模型，还需要采用多领域物理统一建模仿真和联合仿真技术[2]。

Modelica同时支持块图和非因果2种建模方法，基于面向对象的思想使Modelica语言可以方便地实现包括机械、电子、电力、水力、热、控制及面向过程的子系统等物理系统的建模与仿真，并能够进行跨领域、跨学科物理系统的性能分析[3]。Heijde等［4］建立了一种应用于集中供热管网的活塞流管道模型，这个模型在一定程度上能够忽略管道轴向的传热与热扩散问题，与Modelica 有限元体积法管道模型相比更稳定、计算更迅速。张宸博［5］搭建实际换热管网的Modelica 系统模型，并进行水动力特性仿真验证，将仿真计算结果与实际运行结果进行比较,得到总体相对误差都在3%以内，满足工程计算精度要求。Oppelt等[6]成功基于活塞流法和拉格朗日法建立了一种全管网跟踪流体段的瞬态热模型，管铮[7]将这个模型应用于区域冷却管网模拟，验证了该模型的有效性。

1 模型简述

在对供热系统的动态热特性进行研究时，为了研究管道的主要动态热特性，动态数学模型的创建基于以下假设条件[8]：

1）水力工况恒定不变；

2）忽略土壤热惯性；

3）忽略管路中弯头、三通等管件的影响。

1.1 热源模型

以TRNSYSY模型库TESSLibs 17中带效率输入的简单锅炉模型为参考进行建模，为简化模型将锅炉效率定为0.85。在该模型中，进水温度、输入流量、锅炉效率和燃烧效率作为模型的输入，输出流量、出水温度、装置能量损失和消耗燃料量等参数。

当锅炉有液体经过时，且锅炉控制信号设置为1（锅炉启动），则模型首先计算将液体温度从其入口值升高到设定温度所需要的能量见式（1）：

装置消耗的燃料量：

组件部分Modelica实现代码如下：

1.2 动态管道模型

模型使用Modelica开源库IBPSA中的PlugFlow-Pipe活塞流法管道组件，该模型基于能量守恒定律、连续性方程建立热损失计算方程：

式中：ρ表示质量密度；cp是液体的比热；A是管道的截面积；v是流速；T是温度；t是时间；x是管道空间坐标，是单位管长热损失。

利用拉格朗日法，建立无限小长度δx的流体中的能量平衡方程，化简得到：

式中：Tin是管道进口温度；Tout是管道出口温度；Tb是可变温度；R是管道热阻；C是管道壁热容。

该模型使用Modelica 语言规范中spatialDistribution 函数进行建模，并考虑时滞性和管道热惯性对动态热特性的影响，建立了通过管道进出口温度及边界条件计算管道热损失及流体温度降的动态管道模型。

1.3 介质模型

介质模型采用模型库中的Modelica.Media.Water.WaterIF97_Pt，该介质物性参数制定依据IF97标准，模型通过压力和温度确定介质状态点。

2 模型验证及管道动态响应过程研究

2.1 管道模型验证

参考郑进福等[8]使用节点法建立的供热系统动态模型的模拟数据及实验数据，用以验证文章使用的活塞法的动态管道模型。选取热源到换热站长约4 100 m 的管路，利用前述模型假设条件对管路进行简化建模。热源处介质流速在1.16～1.19 m∕s，取1.18 m∕s，模型中热源端水温数据及室外温度数据均使用Modelica 标准库Modelica,Blacks.Souces.TimeTable 组件，将6:00～18:00时段的热源端温度数据输入到管道模型中。

模拟结果如图1 所示，可以看出模拟的结果与测量结果基本吻合，模拟值和实测值的差别较小，实测值与模拟值之差的平均误差约为0.8 ℃，表明所使用的活塞流管道模型满足在热源水温大幅变化管网的模拟要求。

图1 热源温度以及末端测量值模拟值

2.2 管道参数对温度延迟的影响

建立一个管道材料为Q235B碳钢、壁厚为12 mm的DN400直埋预制保温管道，管道保温材料为聚氨酯泡沫，保温层厚度为65 mm，模型结构如图2所示。

图2 模型结构图

2.2.1 管长对温度延迟的影响

采用DN400 管道，且热源以固定质量流量G=200 kg∕s 输送热水，管道及热源内流体介质初始温度均为50 ℃，使用标准库中Modelica.Blocks.Sources.Ramp组件赋予热源内介质一个于400 s温度陡然增加至70 ℃的变化，对比100 m、200 m、300 m、400 m不同管长条件下管道末端温度的动态响应过程。

模拟结果如图3 所示，可以发现在源端温度发生阶跃后，管长100 m 的管道末端温度最先开始响应，最后开始响应的为400 m长管道；同时，4条管道分别在开始响应后的40 s、80 s、170 s、210 s 再次达到稳态。因此，在相同条件下，直径相同的管道，管长越小，动态响应越迅速，且响应所需的时间越短。

图3 不同管长下D N400管道末端温度

2.2.2 管径对温度延迟的影响

采用管长为200 m 的管道，且热源以固定的质量流量G=200 kg∕s 输送热水，管道及热源内流体介质初始温度均为50 ℃，使用标准库中Modelica.Blocks.Sources.Ramp 组件赋予热源内介质一个于400 s 温度陡然增加至70 ℃的变化，对比DN125、DN200、DN300、DN400不同管径条件下管道末端温度的动态响应过程。

模拟结果如图4 所示，可以发现在源端温度发生阶跃后，按照管径由小到大的顺序管道末端温度依次开始响应，且4条管道分别在开始响应后的30 s、55 s、80 s、105 s 再次达到稳态。因此可以得出，在相同条件下，管长相同的管道，管径越小，动态响应越迅速，且响应所需的时间越短。

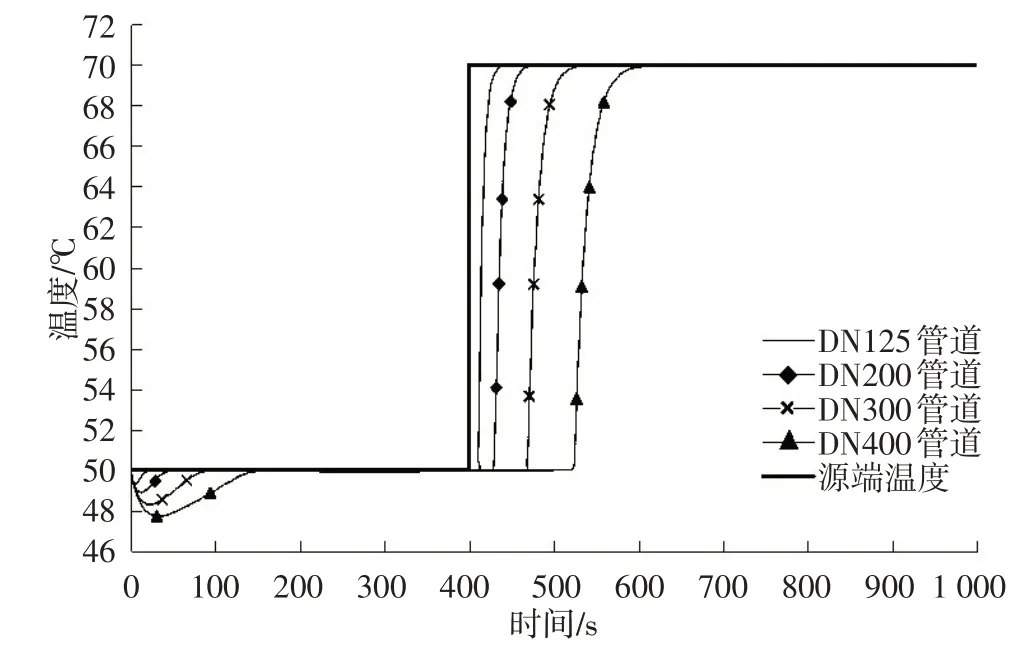
图4 不同管径下200 m管道末端温度

2.2.3 管道单位长度热容量对温度延迟的影响

选取长200 m 的DN400 管道为研究对象，由于管道材质及厚度和保温层材料及厚度均会影响管道单位长度热容量，为更直观地观察结果，假设管道与保温层共用材质及厚度，并对比热容进行理想取值cp=500、1 500、2 500、3 500J∕（kg∙K）,对比不同单位长度热容量末端温度的响应过程。

模拟结果如图5 所示，可以看出，400 s 是源端温度发生阶跃，在源端温度阶跃后的120 s管道末端温度同时开始响应，并分别在开始响应后的105 s、300 s、435 s、480 s完成响应达到稳态。由此可知在相同条件下，单位管长的热容量对反应速度没有影响，但单位管长的热容量越小，完成响应所需时间越短。

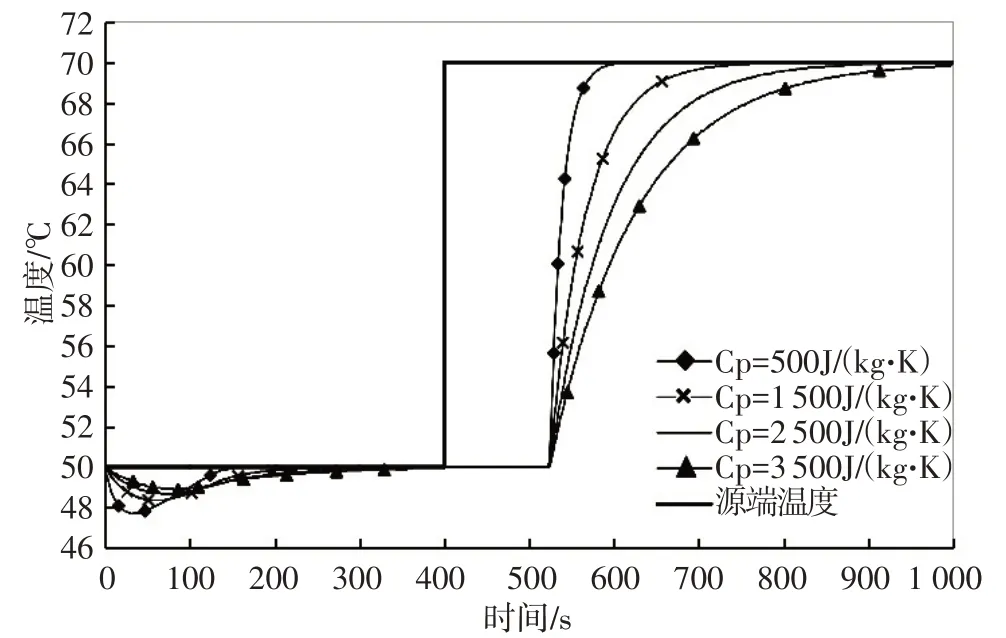
图5 不同单位管长热容量管道末端温度

3 总结

该研究通过供暖实际运行数据验证了活塞流法Modelica管道模型能够满足在热源温度频繁变动条件下的供热系统动态仿真需求，且模型仿真所需时长短，易用性高。同时通过对不同条件下管道参数对供热管道末端温度动态响应过程的模拟，得出以下结论：

1）同管径的管道管长越长，动态响应越迅速，响应所需时间越短；

2）等长的管道管径越小，动态响应越迅速，响应所需时间越短；

3）管道单位管长的热容量对动态响应的反应速度没有影响，但单位管长的热容量越大，完成响应所需时间越长。

此次研究所使用的模型是通过拉格朗日法完成的数学建模，管长管径对于温度动态响应过程的影响可以总结为，无限小长度上的流体段在管段中停留时间越短，动态响应越迅速，响应所需时间越短。在供热设计中，在满足水力工况要求的情况下，遵循较长的管道采用较小的直径，同时在管道外保温材料选择上，选择传热系数小同时比热容低的材料可以一定程度上减少管道热损失以及供热管道温度响应的延迟性，从而降低后期集中供热系统的控制调节难度。