柔度法测算三点弯曲试样疲劳裂纹长度的影响因素

高宇昊, 王 佳, 朱官朋, 房 坤, 翟建飞

(中国船舶集团有限公司第七二五研究所, 洛阳 471023)

在疲劳裂纹扩展速率等试验过程中,采用柔度法可以快捷有效地对裂纹长度进行测算,其基本原理为：对于特定形状的标准试样,由解析法计算出的无量纲弹性柔度EBV/F(E为弹性模量;B为试样厚度;V为裂纹嘴张开位移;F为载荷)和归一化裂纹长度a/W(a为裂纹长度;W为试样宽度)可以用某一函数关系来表达。以三点弯曲试样为例,对应裂纹嘴张开位移的柔度函数如式(1),(2)所示。

3.2141U3+51.516U4-113.03U5

(1)

(2)

式中：S为跨距,S=4W;V/F为柔度;U为计算中间量。

测量并计算裂纹嘴张开位移与载荷的关系V/F,可以获得裂纹的长度,从而实现裂纹长度的自动测算。然而在实际使用时,试样形状、测量误差、弹性模量取值等因素会使测算裂纹长度与真实裂纹长度之间存在偏差[1],余圣甫等[2]在进行单试样法积分-裂纹扩展量阻力曲线测试时发现,用柔度法测算的裂纹长度比用读数显微镜通过九点法测量的裂纹长度小。张亚军[3]在对10MnNi3MoV船用结构钢进行疲劳裂纹扩展速率试验时发现,试验开始时用柔度法推导的弹性模量比钢材弹性模量的典型值低,在柔度函数中使用不同的弹性模量会影响疲劳裂纹扩展速率的试验结果。柔度法测算裂纹长度的精确性与柔度的测量误差、弹性模量、刀口尺寸以及引伸计的安装等因素有关。

一般认为,随着试样厚度的增加,裂纹尖端平面应变状态的比例增加,试样的有效弹性模量E′将介于平面应力状态下弹性模量E和平面应变状态下弹性模量E/(1-ν2)之间(ν为泊松比),从而影响式(1)中的无量纲弹性柔度EBV/F。由于疲劳裂纹扩展速率试样的裂纹前缘近似呈圆弧状,仅测量表面裂纹无法反映实际的裂纹长度。笔者针对不同厚度的三点弯曲试样,在疲劳裂纹扩展速率试验过程中,利用着色剂[4]在不同裂纹扩展阶段对实际裂纹长度进行标记,从而获得柔度法测算裂纹长度与实际裂纹长度的对应关系,进而分析试样厚度、柔度函数关系式的适用条件、材料的弹性模量、裂纹前缘弯曲程度(曲率)、引伸计测量标距等因素对柔度法测算裂纹长度的影响。

1 试验方法

将10Ni6CrCuMoV钢板(板厚为30 mm)按照GB/T 6398—2017 《金属材料 疲劳试验 疲劳裂纹扩展方法》的要求加工成不同厚度的三点弯曲试样,取样位置为板厚中心处,试样长度方向垂直于轧制方向。利用电液伺服疲劳试验机对试样进行疲劳裂纹扩展速率试验,每组3个平行试样,试样公称尺寸及试验参数如表1所示。

表1 试样公称尺寸及试验参数

首先,在缺口试样上测量试样柔度V/F,用疲劳裂纹扩展速率试验最大载荷的0.9倍(0.9Fmax)对试样进行弯曲加载-卸载,为了保证加载的稳定性,加载-卸载周期为10 s,连续加载10次,记录载荷F和对应裂纹嘴张开位移V的值。柔度测量时的载荷-时间曲线如图1所示。

图1 柔度测量时的载荷-时间曲线

接着在试样上预制疲劳裂纹,方法为降K(应力强度因子)法,设置最终阶段的应力强度因子最大值Kmax为28.0 MPa·m0.5,直至预制裂纹长度aa达到0.2W。用图1所示的载荷测量试样柔度,同时从试样缺口处将着色剂滴入裂纹面,裂纹张开时,颜色分子因毛细作用沉积在裂纹尖端,干燥后完成对预制裂纹的标记。

然后进行疲劳裂纹扩展试验,方法恒载荷法,当裂纹长度达到约0.3W(ab)时,暂停试验,用图1所示的载荷测量试样柔度,并用着色剂标记裂纹。干燥后继续进行试验,当裂纹长度达到约0.4W(ac)、0.5W(ad)、0.6W(ae)、0.7W(af)时,用同样的操作测量试样柔度并标记对应裂纹。

最后,试样在裂纹扩展的最后阶段发生弯曲失效,将试样沿裂纹面打开,用显微镜测量标记的裂纹长度。

2 试验结果

柔度测量时采用末5次循环的载荷F和裂纹嘴张开位移V,在最大载荷的50%～90%对V-F曲线求斜率,以获得试样的柔度,根据柔度函数关系式测算裂纹的长度,测算使用的弹性模量为钢铁材料典型值206 GPa。以试样3(厚度为20 mm)为例,不同裂纹长度下的V-F曲线如图2所示。由图2可知：随着裂纹长度的增大,试样柔度V/F增大,当裂纹长度达到约0.7W时,加载柔度和卸载柔度有明显区别,此时试样裂纹尖端已经有较明显的塑性变形,试样不再是近似理想的弹性体,会对柔度函数关系造成一定影响。

图2 试样3在不同裂纹长度下的V-F曲线

采用九点法在显微镜下观察试样断口,测量并计算对应的实际裂纹长度,试样3断口的宏观形貌如图3所示。测量裂纹长度、实际裂纹长度a′和柔度法测算裂纹长度a(1)结果如表2所示。其他试样断口的宏观形貌、裂纹长度测量及测算方法与试样3相同,其中试样1(厚度为10 mm)的尺寸较小,在裂纹长度达到0.7W之前就发生了失效。

图3 试样3断口的宏观形貌

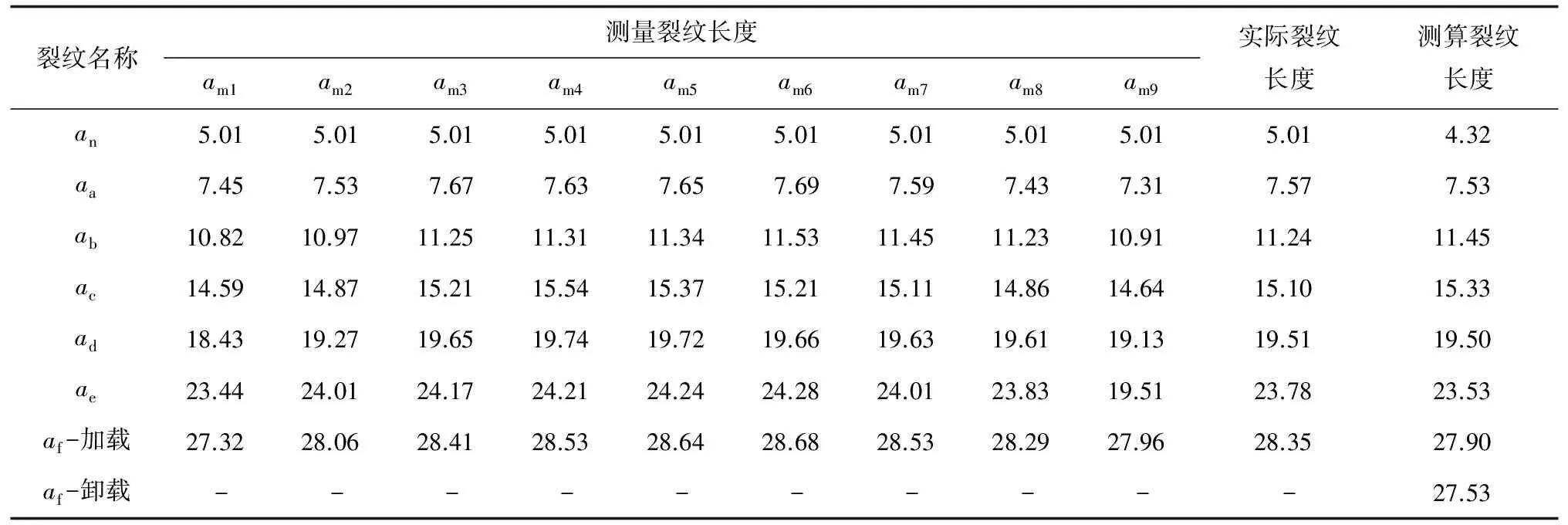
表2 试样3裂纹长度测量结果 mm

由表2可知：柔度法测算裂纹长度与实际裂纹长度之间存在一定的差异,当裂纹长度达到约0.7W(af)时,加载柔度测算的裂纹长度比卸载柔度测算的裂纹长度稍大,且更接近实际裂纹长度。其他试样在裂纹长度达到约0.7W(af)时,加载柔度测算的裂纹长度也更接近实际裂纹长度,因此当裂纹长度达到约0.7W(af)时,采用加载柔度来进行裂纹长度的测算。

3 测算裂纹长度的影响因素

使用柔度法测算裂纹长度a(1)与实际裂纹长度a′的差值来反映柔度法测算裂纹长度的准确性。为了与柔度函数关系式对照,将a(1)和a′进行归一化处理,不同厚度的试样归一化裂纹长度差值[a(1)/W-a′/W]/(a′/W)与归一化实际裂纹长度a′/W的关系如图4所示。由图4可知：当厚度相同时,随着归一化实际裂纹长度的增大,归一化裂纹长度差值的绝对值快速减小,当归一化实际裂纹长度不小于0.3时,归一化裂纹长度差值的变化趋于平缓;当归一化实际裂纹长度小于0.3时,随着试样厚度的增大,归一化裂纹长度差值由大变小,柔度法测算裂纹长度与实际裂纹长度相比先偏大后偏小;当归一化实际裂纹长度不小于0.3,试样厚度不大于的25 mm时,a(1)与a′相差小于5%,认为a(1)有较好准确性;当试样厚度为30 mm时,a(1)比a′偏小,相差大于5%,柔度法测算的裂纹长度与实际裂纹长度有较大偏差。

图4 归一化裂纹长度差值与归一化实际裂纹长度的关系

(3)

3.1 柔度函数关系式的适用条件

ASTM E399-22StandardTestMethodforLinear-ElasticPlane-StrainFractureToughnessofMetallicMaterials附录中指出,三点弯曲试样裂纹嘴张开位移柔度与裂纹长度的关系如式(3),(4)所示。

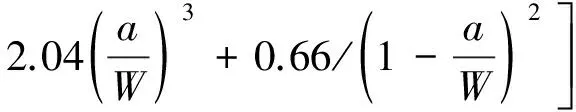
(4)

当0≤a/W≤1时,式(3),(4)的精确度不大于1%;当0.3≤a/W≤0.9时,式(3),(4)与式(1),(2)的等价程度不大于0.05%[7]。因此,若以a/W为自变量,当0.3≤a/W≤0.9时,式(1)可作为式(3)的近似解。由于式(1)与式(3)相比更便于计算,因此将式(1)作为常用柔度函数关系式。

以式(3)中的a(3)/W为自变量,经过计算,a(1)/W与a(3)/W的差值[a(1)/W-a(3)/W]/(a(3)/W)与a(3)/W的关系如图5所示。由图5可知：当a(3)/W≤0.2时,a(1)/W比a(3)/W明显偏小,当a(3)/W=0.15时,差值约为17%,随着a(3)/W的增加,差值快速减小;当a(3)/W≥0.3时,差值小于0.5%。因此,根据柔度函数关系式的适用条件,使用式(1)进行裂纹长度测算时,要求实际裂纹长度a′/W≥0.3是保证测算结果准确的必要条件。

图5 差值[a(1)/W- a(3)/W]/(a(3)/W)与a(3)/W的关系

3.2 有限元方法对柔度函数关系的模拟

利用有限元分析软件对三点弯曲试样的柔度函数关系进行模拟,由于三点弯曲试样和载荷具有对称性,故取试样的一半建立模型,并进行静力学分析。模型主体采用六面体网格,并对裂纹尖端区域进行网格细化,三维模型的网格类型为C3D20R单元(20节点六面体二次减缩积分实体单元),网格尺寸约为1.0 mm。假设材料的弹性模量为206 GPa,泊松比为0.3,施加载荷如表1所示。试样整体处于弹性状态,使用围线积分方式模拟计算裂纹尖端的应力状态,模拟的平直裂纹长度为as,根据裂纹嘴中心处的节点坐标变化计算裂纹嘴张开位移。

根据式(1)和有限元模拟的(V/F)s值,求出对应的a(3)/W,借助数学软件求解出对应的a(4)/W值。在模拟不同裂纹长度as时,不同厚度试样的差值[a(1)/W-as/W]/(as/W)和[a(3)/W-as/W]/(as/W)与as/W的关系如图6所示。由图6可知：当as/W≤0.2时,a(1)/W与as/W差值大于5%;当as/W≥0.3时,a(1)/W与as/W差值小于2%;当as/W≤0.2时,a(3)/W与as/W差值比a(1)/W与as/W差值明显偏小;当as/W≥0.3时,a(3)/W与as/W差值小于2%;当as/W≥0.3时,柔度函数关系式与有限元模拟结果较为符合,侧面验证了柔度函数关系的正确性。

图6 两柔度公式测算裂纹长度与模拟裂纹长度的关系

当试样厚度不大于40 mm时,在平直贯穿型裂纹情况下,裂纹中心的平面应变状态对柔度函数关系没有明显的影响,当as/W≥0.3时,在式(1)中使用材料的弹性模量E进行计算,可以获得较准确的测算裂纹长度。

3.3 裂纹曲率对柔度法测算裂纹长度的影响

在金属材料的疲劳裂纹扩展速率试验中,裂纹中心处的材料处于平面应变状态,承受的应力比试样两侧的应力大,因此中心处的裂纹扩展速率较快,两侧的裂纹扩展速率较慢,裂纹前缘类似圆弧状。用圆弧近似裂纹前缘的形状,根据最大裂纹长度amax、最小裂纹长度amin与试样厚度B之间的几何关系,裂纹前缘的弯曲半径R,圆弧角度2α的计算关系分别如式(5)～(7)所示。

(5)

d=amax-amin

(6)

(7)

根据式(5)～(7)和试验结果,计算当a/W约为0.4时,不同厚度试样的amax-amin值、曲率半径R和圆弧角度2α,结果如表3所示。曲率半径R随试样厚度的变化如图7所示,圆弧角度2α随试样厚度的变化如图8所示。由图7,8可知：随着试样厚度的增大,裂纹的曲率半径R增大,但增大趋势并不明显;随着试样厚度的增大,圆弧角度2α增大,且具有明显的增长趋势。圆弧角度2α不但与曲率半径R有关,还有试样厚度有关,因此对于不同厚度的试样,圆弧角度2α比曲率半径R更能近似地描述裂纹前缘的弯曲程度。

图7 曲率半径R随试样厚度的变化

图8 圆弧角度2α随试样厚度的变化

表3 不同厚度试样的amax-amin值、曲率半径R和圆弧角度2α计算结果

用有限元方法模拟amax/W=0.4时,不同厚度试样的受力状态,圆弧角度2α采用图8中的平均值。不同厚度试样对应的归一化实际裂纹长度a′/W和归一化柔度法测算裂纹长度a(1)/W对比结果如图9所示。由图9可知：a(1)/W比a′/W小,当试样厚度由25 mm增大至30 mm时,a(1)/W比a′/W差值明显增大,由约0.5%增大至约2.0%。说明随着试样厚度的增加,圆弧角度2α增大,影响了裂纹的平直度,柔度法测算的裂纹长度a(1)比实际裂纹长度a′偏小。对于疲劳裂纹扩展速率试验,不同材料的裂纹前缘弯曲程度不同,如果材料裂纹前缘的圆弧角度过大,则不宜采用较厚(厚度不小于30 mm)试样进行试验。

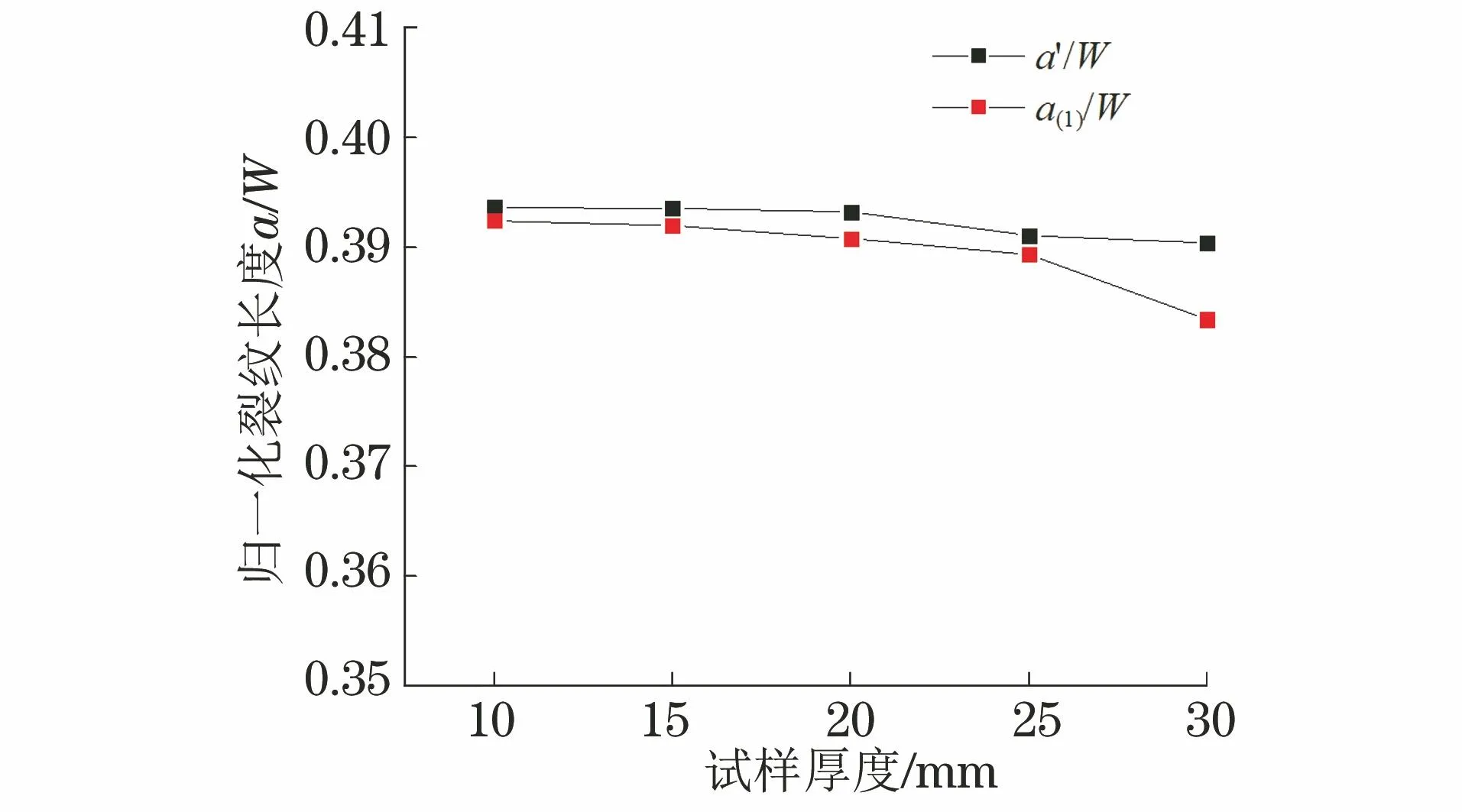
图9 归一化裂纹长度随试样厚度的变化情况

3.4 引伸计标距对裂纹嘴张开位移的影响

裂纹嘴张开位移V是指试样边缘处裂纹面的张开量,实际试验时由于引伸计标距的原因,引伸计测得的裂纹嘴张开位移V′是实际位移V的近似值。三点弯曲加载时,假设试样两侧以裂纹顶端为圆心对称旋转,以试样左半部为例,裂纹嘴张开位移V的计算方法如式(8)～(10)所示。

(8)

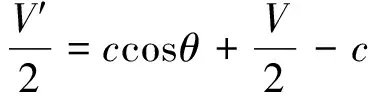
(9)

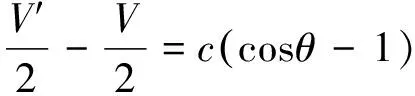
(10)

式中：a为裂纹长度;c为引伸计标距的一半;θ为单侧的旋转角度。

由式(10)可知：引伸计测得的张开位移V′比试样实际的张开位移V小,根据式(1),a(1)/W与柔度V/F是单调递增关系,因此由V′/F得到的裂纹长度会存在偏小的情况;在θ一定的情况下,引伸计标距2c越大,V′/F偏小的程度越大。

根据有限元模拟的结果,引伸计标距为10 mm时对应的柔度V′/F与裂纹嘴张开位移的柔度V/F几乎一致,经过计算,试样在最大载荷时的θ角很小,绝对值|cosθ-1|<0.000 1。对于疲劳裂纹扩展速率试验,试样整体处于弹性状态,裂纹面的张开量较小(θ值较小),引伸计标距对柔度测量的影响可以忽略。对于某些裂纹面张开量较大(θ值较大)的断裂试验,如裂纹尖端张开位移、延性断裂韧性试验等,引伸计标距过大,会造成裂纹嘴张开位移V的测量值偏小,进而影响试验结果。

4 结论

(1) 对于不同厚度的10Ni6CrCuMoV钢三点弯曲试样,当试样厚度不大于25 mm,归一化实际裂纹长度a′/W≥0.3时,柔度法测算裂纹长度a(1)与真实裂纹长度a′相差小于5%,认为a(1)有较好的准确性。

(2) 当a(3)/W≤0.2时,a(1)/W与a(3)/W相比明显偏小,a(3)/W=0.15时,a(1)/W与a(3)/W相差约17%;当a(3)/W≥0.3时,a(1)/W与a(3)/W相差小于0.5%。根据柔度函数关系式的适用条件,使用式(1)进行裂纹长度测算时,要求实际裂纹长度a′/W≥0.3,以保证测算结果准确。

(3) 用有限元方法模拟三点弯曲试样中平直的贯穿型裂纹as,两柔度函数关系式(1)和式(3)在as/W≥0.3时与模拟结果均有较高符合性,a(1)/W、a(3)/W与as/W相差小于2%;当试样厚度不大于40 mm时,裂纹中心的平面应变状态对柔度函数关系没有明显影响,在式(1)中使用材料的弹性模量E进行计算,可以获得较准确的测算裂纹长度。

(4) 用圆弧角度2α来描述裂纹前缘的弯曲程度,根据试验结果,随着试样厚度的增大,2α明显增大,裂纹平直度降低,导致柔度法测算的裂纹长度a(1)比实际裂纹长度a′偏小。对于疲劳裂纹扩展速率试验,不同材料的裂纹前缘弯曲程度不同,如果材料裂纹前缘的圆弧角度过大,则不宜采用较厚(厚度不小于30 mm)试样进行试验。

(5) 在疲劳裂纹扩展速率试验过程中,试样整体处于弹性状态,裂纹面的张开量很小,引伸计标距对柔度测量的影响可以忽略。对于某些裂纹面张开量较大的断裂试验,如裂纹尖端张开位移、延性断裂韧性试验等,引伸计标距过大会造成裂纹嘴张开位移V的测量值偏小,影响试验结果。