基于有限元法的油气田集输管网阴极保护布局优化
曾维国,李曙华,余文正,徐 东,刘博宇,范 峥
(1.中国特种设备检测研究院,北京 100029;2.中国石油长庆油田分公司气田开发事业部,西安 710021;3.西安长庆工程建设监理有限公司,西安 710016;4.中国石油长庆油田分公司第二采气厂,榆林 719000;5.西安石油大学石油工程学院,西安 710065;6.西安石油大学化学化工学院,西安 710065)
近年来,随着全球能源市场需求激增,油气田集输行业发展迅猛,国内外逐渐形成了众多跨国性、全国性或地区性的复杂油气集输管网。目前,全世界最长距离的油气集输管道长度已经达到了200万km以上,而我国“西气东输”项目作为现阶段国内最大的管输工程,对我国东西部的经济快速发展起到不可忽视的作用[1-3]。需要注意的是,由于金属油气集输管道长期处在地下环境中,且经常穿越各种不同类型的土壤、河流和湖泊,特别是土壤冬、夏季的冻结与融化,地下水位变化,以及杂散电流和埋设条件等各种因素都会造成管道外部发生不同程度的腐蚀,严重时甚至会导致管道穿孔[4-8],进而造成油气泄漏并引发火灾,加之这些管道深埋于地下,很难直观地检查其腐蚀状态。因此,为了保证这些集输管道的安全运行,对油气田集输管网进行有效的腐蚀防护是十分必要和迫切的。
阴极保护是指通过向被保护金属表面施加一个外加电流,将被保护金属人为地变成阴极,使金属腐蚀过程中的电子迁移得到抑制,从而显著减弱或避免腐蚀发生的一种电化学保护技术[9-11]。一般来说,阴极保护技术大体上可分为牺牲阳极的阴极保护和外加电流的阴极保护两大类。其中,牺牲阳极的阴极保护是将还原性较强的金属作为保护极,与被保护金属相连构成原电池,还原性较强的金属作为负极发生氧化反应而消耗,被保护金属作为正极就可以避免腐蚀[12-14];而外加电流的阴极保护则是通过外加直流电源以及辅助阳极,迫使电子从土壤流向被保护金属,使被保护金属结构的电位高于周围环境来进行保护[15-16]。与前者相比,外加电流的阴极保护凭借电流可控可调、使用寿命较长、经济效益良好以及保护范围较大等优点,受到了人们越来越多的关注和青睐,成为油气田集输管网最常用、最普遍的一种金属防腐蚀方法[17-18]。
陕北某油气田的生产区域分布在陕、蒙二省13个市、县、旗境内,其管理范围达到8.65万km2,现有埋地油气田集输管线101条,管线总长度约为1 524 km,建成阴极保护站26座。然而,上述阴极保护系统是随着油气田的发展而逐步建成的,这一保护体系的实际运行状态究竟有无进一步提升的空间,还有哪些不足需要改进是目前亟待解决的重要问题。
针对上述问题,笔者首先利用有限元法对现有外加电流的阴极保护系统进行了模型构建,并通过预测管线电位衰减进一步找出该集输管网可能存在的缺陷,然后采用Sobol灵敏度分析确定了显著影响阴极保护效果的关键参数,最后借助粒子群优化(PSO)算法对油气田集输管网的阴极保护效果进行全局化寻优,并提出了具有针对性和可操作性的现场解决方案,以期为油气田阴极保护系统的调整优化提供科学、可靠的理论依据和数据来源。
1 试 验
1.1 外加电流的阴极保护模型建立
首先,根据油气田集输管网埋设的具体特点,利用ANSYS软件中的Design Modeler模块分别建立管道计算单元和土壤计算单元。在理想条件下,油气田集输管道沿线外加电位E和电流I的计算公式见式(1)~(3)。
E=Aeαx+Be-αx
(1)
(2)
(3)
式中:A、B分别为由边界条件确定的常数;rT为单位长度的管道电阻,Ω·m;RT为单位长度的管道过渡电阻,Ω·m。
其次,定义管线和土壤均为各向同性材料,对于管道计算单元,依次输入管道材质、直径、长度、壁厚、防护涂层电阻率以及管道埋深等相关参数;对于土壤计算单元,需要新建材料属性,并根据实际环境添加土壤电阻率,土壤下表面模拟大地无限远处,设置电压约束值为0。
然后,采用有限元法将油气田集输管线沿轴向划分为若干个管段,各管段在有限的结点处相互连接,组成一个代替连续体的管段集合体。同时,分别给出了不同管线竖直距离的约束电压以及来自阴极保护站的加载电压。除此之外,还利用四面体形式对管线和土壤进行了网格划分,并定义了适宜且有效的网格单元尺寸。
最后,添加要求解的项目,如电流、电压等,也可以定义路径,最终得到油气田集输管网的电场云图,并根据此云图读取每一个点的电位值,包括管线的起末点保护电位及测试桩所在位置的电位,观察电位分布趋势,并预测后期管线的电位分布。
需要说明的是,为了进一步验证上述外加电流的阴极保护模型的准确性和可靠性,作者利用均方差(PMSE)对测试桩处的测定电位与模型模拟电位的差异程度进行了表征,见式(4)[19-21]。
(4)
式中:PMSE为均方差;N为测试桩数目;i为测试桩序号;E为测试桩测定电位,mV;E′为模型模拟电位,mV。
本文中所涉及的外加电流的阴极保护模型建立均由ANSYS 14.5完成。
1.2 Sobol灵敏度分析
Sobol灵敏度分析作为一种基于方差的全局敏感性分析方法,其非线性和鲁棒性都远远优于局部敏感性分析方法,它不但可以计算各个因素对响应值的独立敏感性,同时还能计算交互作用下各个因素对响应值的总敏感性。当某一因素的一阶敏感性系数和总敏感性系数相差较大时,即认为该因素与其他参数之间可能存在明显的交互作用[22-25]。
Sobol灵敏度分析将基于模型输出的总方差V分解为单个变量方差与变量之间相互作用产生的方差的线性组合,见式(5)。
(5)
式中:Vi为第i个输入变量xi的方差;Vii′为第i个输入变量xi和第i′个输入变量xi′之间的相互作用产生的方差;m为输入变量的总数。上述方差均可由Monte Carlo法进行估计。
输入变量对响应值的敏感性系数计算公式见式(6)和(7)。
Si=Vi/V
(6)
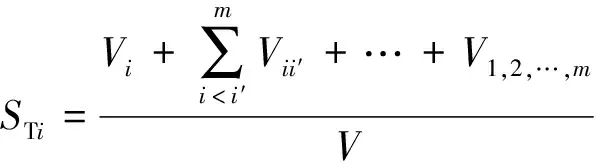
(7)
式中:Si为一阶敏感性系数;STi为总敏感性系数。
本文中所涉及的Sobol灵敏度分析均由MATLAB 8.0.0.783计算完成。
1.3 PSO算法全局寻优
在D维可解空间中初始化由l个粒子组成的种群W,位置、速度和适应度等指标被用来表示这些粒子的特征。若第u个粒子在D维可解空间中运动,它的位置可表示为Eu=[eu1,eu2,…euo,…euD]T,速度可表示为vu=[vu1,vu2,…vuo,…vuD]T,而适应度则由对应管线的阴极保护外加电位表示,其值大小代表了粒子的优劣。粒子在D维可解空间中每变化一次位置,就计算一次适应度,并通过比较粒子的新适应度与个体极值PBu=[PBu1,PBu2,…PBuo,…PBuD]T、群体极值GBu=[GBu1,GBu2,…GBuo,…GBuD]T,达到不断最优化个体极值和群体极值的目的[26-27]。
同时,粒子在每一次位置变化过程中还通过个体极值、群体极值来实现自身位置和速度的迭代更新,其公式见式(8)和(9)。
(8)
(9)
式中:θ为线性递减惯性权重;g1、g2为加速度因子;r1、r2均为分布于[0,1]之间的随机数;f为当前迭代次数。
线性递减惯性权重较大,则更有利于进行全局寻优;线性递减惯性权重较小,则更有利于进行局部寻优。因此,本文还需对粒子进化过程中的惯性权重进行了动态调整,使得线性递减惯性权重在迭代初期具有较强的全局搜索能力,而在迭代后期具有较强的局部搜索能力[28-29],见式(10)。
(10)
式中:θf为迭代次数为f的惯性权重;F为最大迭代次数;θ0为初始惯性权重;θF为迭代至最大次数时的惯性权重。
本文中所涉及的PSO算法全局寻优均由MATLAB 8.0.0.783完成。
2 结果与讨论
2.1 外加电流的阴极保护模型验证
根据2019年陕北某油气田管线普查提供的实际运行数据,随机选取10条油气田集输管线进行外加电流的阴极保护模型验证,具体结果详见表1。

表1 外加电流的阴极保护模型验证结果
由表1可知,对于外加电流的阴极保护模型来说,与测试桩测定电位相比,模型模拟电位的最大均方差为13.68,最小均方差为2.46,平均均方差为7.17,它们的误差普遍在工程允许范围之内。这表明该模型能够准确、可靠地反映出油气田集输管网的电位分布现状,是较为理想的改造优化基础模型。
2.2 阴极保护效果的全局敏感性分析结果
在建立外加电流的阴极保护模型的基础上,通过Sobol灵敏度分析方法考察了管道材质、管道直径、管道长度、管道壁厚、防护涂层电阻率、管道埋深和土壤电阻率等因素对油气田集输管网阴极保护效果的影响,其一阶敏感性系数及总敏感性系数详见图1。

图1 某油气田集输管网阴极保护效果的全局敏感性分析结果
由图1可知,鉴于防护涂层电阻率的一阶敏感性系数最高,土壤电阻率、管道埋深、管道材质、管道壁厚和管道长度的一阶敏感性系数次之,管道直径的一阶敏感性系数最小。这表明改变防护涂层电阻率等一阶敏感性系数较大的因素会对油气田集输管网的阴极保护效果产生较大影响。同时,土壤电阻率、防护涂层电阻率以及管道埋深的一阶敏感性系数与总敏感性系数的差值分别达到了0.160 6、0.127 0、0.122 2,这表明这些因素与其他参数之间可能存在明显的交互作用,因此在后续阴极保护效果优化过程中应当予以特别注意。
2.3 基于PSO算法的油气田集输管网阴极保护优化
按照GB/T 21448-2017《埋地钢质管道阴极保护技术规范》、GB/T 21246-2020《埋地钢质管道阴极保护参数测量方法》的相关要求,油气田集输管网的阴极保护电位必须达到最小保护电位,若它的电位比最小保护电位正,则油气田集输管网可能发生金属腐蚀。由于电位的大小直接取决于使用的参比电极,故作者选择铜/饱和硫酸铜(CSE)作为参比电极,设定-850 mV作为此阴极保护系统需要达到的最小保护电位。
在现有工况条件下,当油气田在役阴极保护站数目为26座,集输管线数目为101条(包括176个管网节点)时,以油气田集输管网得到阴极保护系统有效覆盖(即多站保护下各油气田集输管线的保护电位不大于-850 mV)最大化为目标值,利用MATLAB 8.0.0.783调用基于ANSYS APDL语言汇编的外加电流的阴极保护模型,通过randn()函数产生一个种群粒子个数为200、每个粒子的维数为26(即每个阴极保护站所处的管网节点位置)且符合高斯分布的输入参数随机矩阵形成初始种群,通过PSO算法对其进行全局性优化。其中,粒子适应度由外加电流的阴极保护模型计算得到。一般来说,PSO算法的终止条件包括设定最大迭代次数或全局最优位置来满足最小界限两种,这里选择前者作为终止条件,即当粒子进化迭代次数达到50 000时,基于PSO算法的外加电流的阴极保护模型将停止迭代,并输出相应的优化结果。
为了进一步提高粒子有效跳出先前搜索到的优化值位置和找到更优值的可能性,作者还在PSO算法中引入了变异算子(设为0.7),即在粒子每次更新后,再以一定概率分别对26座阴极保护站的管网节点位置进行重新初始化以保持种群的多样性,从而帮助粒子在更大的空间内展开全局最优值搜索。同时,为了更好地平衡PSO算法的全局搜索能力与局部搜索能力,将PSO算法的初始惯性权重、迭代至最大次数时的惯性权重分别设定为0.8和0.6,以期在最大程度上提升PSO算法的综合性能。
由图2可知,当利用PSO算法对油气田集输管网的阴极保护效果进行优化时,粒子经过50 000次进化迭代后,各阴极保护站均处在适宜的管网节点位置,此时最佳阴极保护系统有效覆盖率高达99.14%,较现有工况下的87.42%增加了11.82%,优化效果显著。需要说明的是,当粒子进化迭代次数达到47 700时,此算法实际上已成功搜索到该值并维持至冗余迭代终止,这表明基于PSO算法的油气田集输管网阴极保护效果全局寻优不仅能够大幅提高各阴极保护站布局的合理性,同时还可以进一步确保多站保护下各油气田集输管线的保护电位不大于最小保护电位,从而有效避免了金属腐蚀的损害,这为油气水集输管网的长周期、稳定、安全运行提供了必要的理论支撑和数据来源。

图2 PSO算法全局最优值搜索过程
3 结 论
(1) 针对金属油气集输管道在实际生产过程中可能存在的腐蚀穿孔问题,外加电流的阴极保护凭借电流可控可调、使用寿命较长、经济效益良好以及保护范围较大等优点,成为油气田集输管网最常用、最普遍的一种金属防腐蚀方法。
(2) 外加电流的阴极保护模型模拟电位的最大均方差为13.68,最小均方差为2.46,平均均方差为7.17,它们与测试桩测定电位的误差普遍在工程允许范围之内,故该模型能够准确、可靠地反映出油气田集输管网的电位分布现状,是较为理想的改造优化基础模型。
(3) 改变防护涂层电阻率、土壤电阻率等一阶敏感性系数较高的因素会对油气田集输管网的阴极保护效果产生较大影响。同时,土壤电阻率、防护涂层电阻率以及管道埋深的一阶敏感性系数与总敏感性系数的差值均较大,表明这些因素与其他参数之间可能存在明显的交互作用,应当予以特别注意。
(4) 当利用PSO算法对油气田集输管网的阴极保护效果进行全局化寻优时,该模型经过47 700次粒子进化迭代后,最佳阴极保护系统有效覆盖率高达99.14%,较优化前的87.42%显著增加了11.82%,优化效果显著。

