Q-homotopy analysis method for timefractional Newell-Whitehead equation and time-fractional generalized Hirota-Satsuma coupled KdV system

Di Liu,Qiongya Gu and Lizhen Wang

Center for Nonlinear Studies,School of Mathematics,Northwest University,Xi’an,710127,China

Abstract In this paper,two types of fractional nonlinear equations in Caputo sense,time-fractional Newell–Whitehead equation (FNWE) and time-fractional generalized Hirota–Satsuma coupled KdV system (HS-cKdVS),are investigated by means of the q-homotopy analysis method (q-HAM).The approximate solutions of the proposed equations are constructed in the form of a convergent series and are compared with the corresponding exact solutions.Due to the presence of the auxiliary parameter h in this method,just a few terms of the series solution are required in order to obtain better approximation.For the sake of visualization,the numerical results obtained in this paper are graphically displayed with the help of Maple.

Keywords: fractional Newell–Whitehead equation,fractional generalized Hirota–Satsuma coupled KdV system,approximate solution,q-homotopy analysis method

1.Introduction

Fractional calculus,a generalization of classical calculus,was proposed by L’Hospital in 1695 and is more suitable than classical calculus for simulating some real-world problems.The advantages of the fractional differential operator are its nonlocality and ability to describe the memory effects of the system.Therefore,fractional calculus has attracted more and more attention in many applied fields,such as biology,physics,rheology,signal processing,electrochemistry [1–6],etc.It is well known that the construction of the exact solutions of fractional partial differential equations(FPDEs)is an important problem.Consequently,many scholars have introduced numerous methods to seek the solutions,such as the Lie symmetry analysis method [7–9],Adomian decomposition method [10],homotopy analysis transform method [11],Laplace transform collocation method [12],functional separation variables method[13],residual power series method[14],sub-equation method [15],homotopy perturbation method[16,17],invariant subspace method [18],auxiliary function method [19,20] and the classical Mittag-Leffler kernel [21].

An approach called the homotopy analysis method(HAM) was first proposed by Liao [22,23] in 1992.The HAM forms a continuous mapping from the initial conjecture to the exact solution after selecting auxiliary linear operators.The HAM contains the auxiliary parameter to determine the convergence of the solution.Later,in 2012,the q-homotopy analysis method (q-HAM) was introduced by El-Tawil and Huseen in[24]and it is one of the most effective methods for solving nonlinear PDEs.It is actually an improvement of the embedding parameterq∈[0,1] in the HAM ton≥1 appearing in the q-HAM.Moreover,the q-HAM contains the fractional factor that gives better convergence than the HAM.Recently,the method has been generalized and applied to some fractional PDEs,such as time-space fractional Fokker–Planck equations [25],time-fractional Ito equation and Sawada–Kotera equation [26],time-fractional Korteweg–de Vries and Korteweg–de Vries–Burgers equations [27] and time-space fractional gas dynamics equation [28].

In this paper,on the one hand,we consider the timefractional Newell–Whitehead equation (FNWE) [29],

where 0 ＜α ≤1 is a parameter describing the order of the time-fractional derivative.Here and hereafter,is the Caputo fractional differential operator with order α.Physically,to solve FPDEs,we need to specify additional conditions in order to produce a solution.Compared with other fractional operators,Caputo fractional operator has many advantages.First,its initial conditions have physical meaning.Second,the lower limit of integration in its definition can be arbitrarily selected and does not necessarily start from 0,which means that the reference interval can be freely regulated to make the equation have short-term memory.Third,the Caputo fractional derivative of a constant is 0.Equation(1)can be considered as a generalization of the Newell–Whitehead equation (NWE).The NWE can simulate the interaction between the effect of the diffusion term and the nonlinear effect of the reaction term.Functionuis denoted as the distribution of temperature in an infinitely thin and long rod or as the flow rate of a fluid in an infinitely long pipe with a small diameter [30,31].The NWE has been widely used in mechanical,chemical and bio-engineering.Furthermore,some approaches,such as the reduced differential transform method [32],Adomian decomposition methods[33] and variational iteration method [34],have been developed to solve the FNWE.

On the other hand,we consider the following timefractional generalized Hirota–Satsuma coupled KdV system(HS-cKdVS):

The generalized HS-cKdVS describes the interaction between long waves with different dispersion relations [35].In this system,u(x,t),v(x,t) andw(x,t) are the amplitude of the wave modes as functions of space variablexand time variablet.Recently,some researchers have investigated this system using different methods.Abbasbandy studied the approximate analytical solution of the generalized HS-cKdVS via the homotopy analysis method [36].Prakash and Verma[37] employed q-homotopy analysis Sumudu transform method and residual power series method to find the analytical solution of system (2).Some exact solutions of system(2)were constructed by Saberi and Hejazi using the invariant subspace method with Caputo sense [38].Martínez,Reyes and Sosa [39] obtained the analytical solutions by applying the sub-equation method for the time-space fractional generalized HS-cKdVS.

In this paper,we have applied the q-HAM to solve the time FNWE and the time-fractional generalized HS-cKdVS with different initial conditions,because it is too difficult to find the exact solution of the two equations,and the proposed method can be used to find the approximate solution of these two equations,which is helpful for a deeper understanding of the proposed equations at a later stage.Keeping the above facts in mind,this paper is the first study to investigate the approximate solutions of the time FNWE and the time-fractional generalized HS-cKdVS with the help of the q-HAM.

The rest of the study is set out as follows.Some basic definitions and formulas related to fractional calculus are provided in section 2.The basic definition of the q-HAM is introduced in section 3.In section 4,we intend to use the q-HAM to solve equation (1) and system (2).We conclude this paper in section 5.

2.Preliminaries

In this section,we introduce some definitions and formulas related to fractional calculus,which will be used throughout the paper.

Definition 2.1.[1] The Riemann–Liouville fractional integral operator of order α of functionf(t) is given as,

Definition 2.2.[1] Forn∈Nandn-1 ＜α＜n,the Caputo fractional derivative of order α of functionf(t) is defined by,

Lemma 2.1.[1]Letγ＞0andt＞ 0.Then,

3.Description of the q-homotopy analysis method

Consider the nonlinear fractional differential equation of the form,

where N is a nonlinear operator,denotes the Caputo fractional derivative,(x,t)are independent variables,f(x,t)is the given function,whileu(x,t) is an unknown function.Construct the zeroth-order deformation equation as follows:

wheren≥1,is called an embedded parameter,h≠0 is an auxiliary parameter,H(x,t)is a non-zero auxiliary function,L is an auxiliary linear operator andu0(x,t) is the initial guess ofu(x,t).Clearly,whenq=0 and,we can obtain the following result:

respectively.Thus,asqrises from 0 to,the solution φ(x,t;q)ranges from the initial guessu0(x,t)to the solutionu(x,t).Assume thatu0(x,t),L,handH(x,t) are appropriately selected so that the solution φ(x,t;q)of equation(6)exists forThe expansion of the function φ(x,t;q) in Taylor series form gives:

Differentiating zeroth-order deformation equation(6)mtimes with respect to the embedding parameterq,settingq=0 and dividing them bym!,we can derive the followingmth-order deformation equation:

Applying the inverse operator-L1to both sides of equation (12) and after simplification,um(x,t) can be presented by,

Remark 1.It needs to be emphasized thatum(x,t)form≥1 is controlled by the linear equation (12)with linear boundary conditions from the original problem.The presence of factorcan produce more opportunities for convergence and even better and faster convergence than the standard HAM.In particular,whenα=1 andn=1 in equation(6),the standard HAM can be achieved.

The convergence and error analysis of the q-HAM are discussed in the following theorems,which shows that the convergence of the q-HAM is more accurate than the convergence of the HAM.

Theorem 3.1.[40]Ifthenonlinearoperatorispreservedon thepowerseriesinq,thesolutionofequation(6)together withequation(5)existsasapowerseriesinthefollowing:

Theorem 3.2.[40]ConsideraBanachspace(A,‖·‖)with

A⊂R.Supposethattheinitialestimationu0(x,t)remainsinsidetheballofthesolutionu(x,t).Letrbeaconstant,thenforaprescribedvalueofhand0 ＜r＜n,ifforallk,

4.Applications of the q-HAM

In this section,the q-HAM is used to construct the analytical solutions of time FNWEs and time-fractional generalized HScKdVS to verify the effectiveness of the previous q-HAM algorithm.The results of this study are graphed by Maple.

4.1.The time-fractional Newell-Whitehead equation

In this section,we construct the series solutions of time FNWE (1) with two different initial conditions with the help of the q-HAM.

Example 4.1.Consider the time FNWE (1) and its initial condition is given as follows:

which was derived in [33].

Choose the linear operator:

with the propertyL [r]=0,whereris a constant.Then,we define a nonlinear operator as,

We construct the zeroth-order deformation equation as follows:

TakingH(x,t)=1,the so-calledmth-order deformation equation is:

with initial condition form≥1,um(x,0)=0,where

The simple transformation of equation (21) yields that,

From (19) to (23) and lemma 2.1,we arrive at the components of the solution of equations (1) and (17) form≥1:

and

Proceeding in similar steps,the remaining iterationsum(x,t)(m=3,4,5,…) can be obtained.Therefore,the series solution of equations (1) and (17) obtained by the q-HAM is

Equation(26)is the appropriate solution to equations(1)and (17) in terms of convergence parametershandn.Moreover,choosingn=1,α=1 andh=-1,the series solutionof equations (1) and (17) converges to its exact solution [34] asN→∞:

With the help of the 3D plots,we demonstrate the wave propagation pattern of the wave along thex-axis.Figure 1 presents the plots of the approximate solution,exact solution and absolute error whenh=-0.44,n=1 and α=1 for equations (1) and (17).It is worth pointing out that the numerical solution obtained by the q-HAM and the exact solutionu(x,t) are almost identical in figures 1(a) and (b).Figure 2 displays the behavior of the flow velocityu(x,t) for distinct values of α atx=1,h=-1 andn=1.We note that the q-HAM solution increases with the increase intin figure 2.Figure 3 exhibits the behavior of the flow velocityu(x,t)for different values ofnatx=1,h=-1 and α=0.2.It can be seen from figure 3 that as the values ofhincrease,the q-HAM solutionu(x,t) decreases.In figure 4,different values of the convergence control parameterhare selected to minimize residual error and guarantee the convergence of the series solution by choosing the appropriate value ofh.

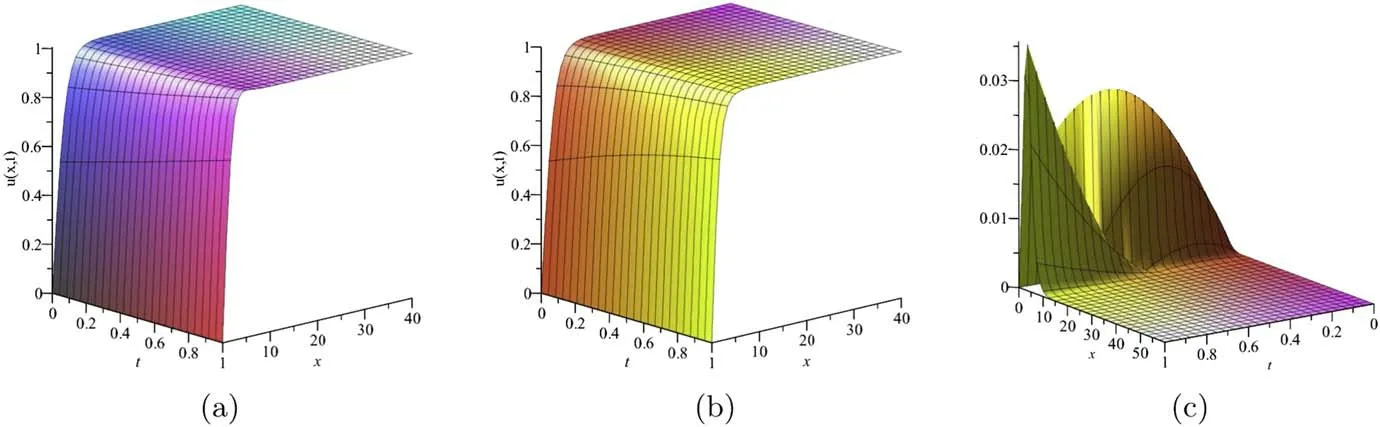
Figure 1.(a).q-HAM solution for Ex.4.1.(b).Exact solution for Ex.4.1.(c).Abs.error=|uexa.-uq-HAM| for Ex.4.1.

Figure 2.Plot of u(x,t) versus time for different values of α for Ex.4.1.

Figure 3.Plot of h curves for Ex.4.1.with fixed x=1 and α=0.2 at different values of n.

Figure 4.Plot of h curves for Ex.4.1.with fixed n=1 and x=1 at different values of h.

Example 4.2.Consider equation (1) with another initial condition given in [34] listed as follows:

Applying (19) to (23),we derive the components of the solution of equations (1) and (28) using the q-HAM successively as follows:

The rest ofum(x,t) (m=3,4,5,…) follows the same approach.Then,the series solution of equations (1) and (28)is,

Equation(31)is the appropriate solution to equations(1)and(28) in terms of convergence parametershandn.Moreover,whenn=1,α=1 andh=-1,the series solutionof equations(1)and(28)converges to its exact solution [34] asN→∞:

The wave propagation pattern of the wave along thexaxis can be seen from the 3D plots.Figure 5 gives the plots of the approximate solution,exact solution and absolute error whenh=-0.45,n=1 and α=1 for equations(1)and(28).It can be observed that the numerical solution obtained by the q-HAM and the exact solutionu(x,t)are consistent with each other in figures 5(a) and (b).Figure 6 demonstrates the behavior of the flow velocityu(x,t)for distinct values of α atx=1,h=-1 andn=1 and indicates that the q-HAM solution increases with the increase in α.Figure 7 displays the behavior of the flow velocityu(x,t)for different values ofnatx=1,h=-1 and α=0.2.It is clear from figure 7 that as the values ofhincrease,the q-HAM solutionu(x,t)decreases.In figure 8,different values of the convergence control parameterhare selected to minimize residual error.

Figure 5.(a).q-HAM solution for Ex.4.2.(b).Exact solution for Ex.4.2.(c).Abs.error=|uexa.-uq-HAM| for Ex.4.2.

Figure 6.Plot of u(x,t) versus time for different values of α for Ex.4.2.

Figure 7.Plot of h curves for Ex.4.2.with fixed x=1 and α=0.2 at different values of n.

Figure 8.Plot of h curves for Ex.4.2.with fixed n=1 and x=1 at different values of h.

Figure 9.Plots of q-HAM solutions for Ex.4.3 when c0=1.2,c1=0.1,β=1.2 and k=0.1.

Figure 10.Plots of the exact solutions for Ex.4.3 when c0=1.2,c1=0.1,β=1.2 and k=0.1.

Figure 11.Plots of Abs.error for Ex.4.3 when c0=1.2,c1=0.1,β=1.2 and k=0.1.

4.2.The time-fractional generalized HS-cKdVS

This section is dedicated to the construction of the approximate solution of system (2) with two different initial conditions through the q-HAM.

Example 4.3.Discuss the time-fractional generalized HScKdVS (2) subject to the following initial conditions introduced in [35]:

wherek,c0,c1≠0and β are arbitrary constants.

Introduce the following linear operators:

wherei=1,2,3.Let φi≜φi(x,t;q) and the nonlinear operators can be provided as,

Construct the zeroth-order deformation equations as,

ChoosingH(x,t)=1,themth-order deformation equations can be given by,

The simple transformation of equation (37) yields that,

Combining(15),(37),(38)and(39)with lemma 2.1,the components of the solution can be obtained by continuous application of the q-HAM:

Moreover,we can repeat the above process to deduce the formulas ofum(x,t),vm(x,t)andwm(x,t)(m=3,4,5,…)and deduce the following series solution of system (2):

Figures 9–11 show the plots of the approximate solution,exact solution and absolute error whenh=-1,n=1,α=1,c0=β=1.2 andc1=k=0.1 for system (2)with the initial conditions (33),respectively.The numerical solution obtained by the q-HAM is almost similar to the exact solution,as observed in figures 9 and figure 10.The effect of the various parameters and variables on the amplitude of the wave modes is shown from figures 12–14.Figure 12 presents the behavior of the numerical solution for distinct values of α atx=2,h=-1 andn=2.It is easy to see that the q-HAM solution increases with increasingtin figure 12.Figure 13 exhibits the behavior for different values ofnatx=2 and α=0.3.We note from figure 13 that as the values ofhincrease,the q-HAM solution decreases.In figure 14,diverse values of the convergence control parameterhare selected to lessen the error.

Figure 12.Plots of u(x,t),v(x,t),and w(x,t) for Ex.4.3 with fixed c0=β=1.2,c1k=0.1,x=2n=2 and h=1 at different values of α.

Figure 13.Plots of h curves for Ex.4.3 at different values of n when c0=β=1.2,c1=k=0.1,x=2 and α=0.3.

Figure 14.Plots of h curves for Ex.4.3 at c0=β=1.2,c1=k=0.1,x=n=2 and α=0.3 with increasing values of t.

Figure 15.Plots of q-HAM solutions for Ex.4.4.when c0=1.2,c1=0.1,β=1.2 and k=0.1.

Figure 16.Plots of the exact solutions for Ex.4.4.when c0=1.2,c1=0.1,β=1.2 and k=0.1.

Figure 17.Plots of Abs.error for Ex.4.4.when c0=β=1.2 and c1=k=0.1.

Example 4.4.For system (2),we take the new initial conditions introduced in [42]:

wherek,c0,c2≠0and β are arbitrary constants.

Similarly,from(37)to(39),we derive the components of the solution as follows:

In the same way,um(x,t),vm(x,t)andwm(x,t)(m=3,4,5,…) can be derived.Accordingly,the series solution of system(2) by the q-HAM in series form is provided as follows:

Figures 15–17 display the plots of the approximate solution,exact solution and absolute error whenh=-1,n=1,α=1,c0=β=1.2 andc1=k=0.1 for system (2)with the initial conditions(44),respectively.As can easily be discovered from figures 15 and 16,the numerical solution obtained by the q-HAM coincides with the exact solution.Figures 18–20.show the effect of the various parameters and variables on the amplitude of the wave modes.Figure 18 depicts the behavior of the numerical solution for distinct values of α atx=2,h=-1 andn=2.It is realized that the q-HAM solution increases with the increase intin figure 18.Figure 19 exhibits the behavior of the numerical solution for diverse values ofnatx=2 and α=0.3.It can be seen from figure 19 that as the values ofhincrease,the q-HAM solution decreases.In figure 20,different values of the convergence control parameterhare selected to minimize residual error and guarantee the convergence of the series solution by choosing the appropriate value ofh.

Figure 19.Plots of h curves for Ex.4.4.at different values of n when c0=β=1.2,c1=k=0.1,x=2 and α=0.3.

Figure 20.Plots of h curves for Ex.4.4.at c0=β=1.2,c1=k=0.1,x=n=2 and α=0.3 with increasing values of t.

5.Conclusion

In this present study,the new approximate solutions of the time FNWE and the time-fractional generalized HS-cKdVS are successfully constructed by means of the q-HAM.The results show that the q-HAM gives the solution in the form of a convergent series without using linearization and perturbation.In addition,it is shown from the absolute truncated error image that the results of the present method are in excellent agreement with the exact solution.The auxiliary parameterhandn(n≥1) used in the proposed method describe the nonlocal convergence.Therefore,the investigation of this paper shows that the q-HAM is an effective and powerful tool to solve nonlinear FPDEs with the sense of Caputo derivative.

Funding

This study is supported by the National Natural Science Foundation of China (Grant No.12 271 433).

Conflict of Interest

The authors declare that they have no conflicts of interest.

ORCID iDs