Mott insulator-density ordered superfluid transition and ‘shamrock transition’ in a frustrated triangle lattice

Ce Wang and Yu Chen

1 School of Physics Science and Engineering,Tongji University,Shanghai,200092,China

2 Institute for Advanced Study,Tsinghua University,Beijing,100084,China

3 Graduate School of China Academy of Engineering Physics,Beijing,100193,China

Abstract Density order is usually a consequence of the competition between long-range and short-range interactions.Here we report a density ordered superfluid emergent from a homogeneous Mott insulator due to the competition between frustrations and local interactions.This transition is found in a Bose–Hubbard model on a frustrated triangle lattice with an extra pairing term.Furthermore,we find a quantum phase transition between two different density ordered superfluids,which is beyond the Landau–Ginzburg(LG)paradigm.A U(1)symmetry is emergent at the critical point,while the symmetry in each density ordered superfluid is Z2 × Z3.We call the transition a ‘shamrock transition’,due to its degenerate ground state in the parameter space being a shamrock-like curve rather than a circle in an LG-type transition.Effective low energy theories are established for the two transitions mentioned above and we find their resemblance and differences with clock models.

Keywords: frustrated magnets,superfluid,mott insulator,density wave ordered phase,clock model

1.Introduction

The coexistence of superfluid and density order is usually thought to be exotic.The reason is that the density order usually means lack of mobility and superfluidity means dissipativeless flow where mobility is strong.However,closer scrutiny tells us a density-ordered superfluid is a condensation that happens at a finite momentum,which makes it less contradictory.This kind of phase can be achieved by competition between short-range and long-range interactions [1–8],such as in cavity Bose–Einstein condensate(BEC)systems[9–13],in dipolar gases systems[14–17],or by dispersion modification such as the stripe phase in BEC with spin-orbit-coupling [18–24].Among these mechanisms,either we need a finite-range interaction or a dispersion modification to locate kinetic energy minimal to a finite momentum state.Here,we try to go beyond these two mechanisms.

In this paper,we give an example of a density ordered superfluid phase by the competition between frustrations and local interactions.To be more specific,we find a homogenous Mott insulator(MI)to density wave ordered superfluid(DWSF)transition in a frustrated triangle lattice system with interacting bosons.The Bose–Hubbard model(BHM)on a triangular lattice with positive hopping strength is well studied previously.A connection is found between the frustrated BHM and the Kosterlitz–Thouless (KT) phase.A 120-degree chiral order is developed to reconcile the requirement of the homogeneous phase by strong local interactions and the sign structure required by frustration,but no density order is presented [25].It seems that the presence of frustrations and local interactions is not enough for a DWSF.However,a DWSF is generated to avoid frustration when we add an on-sie pairing term[26].Practically,these on-site pairing terms are natural in Kerr cavity systems[27],exciton-polariton systems[28,29]as well as in the nuclear magnetic resonance (NMR) systems with an anti-squeezing technique[30].The previous work focuses on a weak interaction region where a homogeneous MI to DWSF transition is missing.Here in this paper,we study the Mott region and find a homogeneous MI to DWSF transition,which justifies the density order being emergent from spontaneously symmetry breaking (SSB).

Figure 1.(a)Illustration of the model.A Bose–Hubbard model on a triangle lattice with pair generation term.(b)Typical phases for fixed η/U with increasing J/U.There are Mott insulator,non-chiral supersolid,and chiral supersolid phases.When J/U is small,the first phase is the homogenous Mott insulator phase.The yellow color in(b)means the density is homogenous.Between T1 and T2,there is a supersolid phase.The red and blue mean these bosons are condensed in opposite phase 0 and π.There is a density order as the superfluid density is only nonzero on the rings of the triangle lattice.As in this phase,the chiral symmetry is not broken.Thus,we name it as a nonchiral supersolid phase.There is no superfluid density in the hexagon center.When J/U ＞T2,then the system turns to a different supersolid phase.In this phase,the phase 0 atoms are condensed in the hexagon center and have a larger density.The phase π condensation is shown in blue on the rings of the hexagon with a smaller superfluid density.Here it is also a non-chiral superfluid.At J/U=T2,the transition is first order,and the system rotates from one kind of non-chiral supersolid to another non-chiral supersolid.Here we find this transition is very special,and there is an emergent U(1) symmetry at the transition point.

In the following,we will first present our model and then we give the phase diagram by a standard mean-field theory method.Then we study the transition mechanism by an effective theory.We find three typical phase transitions as we increase the frustration with fixed pairing energy.The first transition is a MIDWSF transition.Distinct with frustrated BHM without a pairing term,this DWSF is non-chiral.The second transition is between two non-chiral DWSFs.In this transition,an emergent U(1) symmetry is found at the critical point.We call it a‘shamrock transition’ because its degenerate ground state in the parameter space is a shamrock-like curve rather than a circle in an LG-type transition.The third one is a chiral symmetry broken transition where a chiral ordered DWSF is generated.Here we focus on the first two transitions(figure 1(b)).Then by perturbation expansion of order parameters,we find effective theories for MI-DWSF transition and the ‘shamrock transition’.We find the shamrock transition is closely related to clock models and gives a different direction to study KT transitions.

2.Model

Here we consider a BHM on a triangular lattice with an onsite pairing term,

where

Before we dive into the details of the ground state properties of equation (1),let us first analyze its symmetry.One can see there is a translational symmetry on the lattice sites.Besides,there is aU(1)symmetry if η=0,which is an invariance under transformationIt is broken to aZ2symmetry→±when the pairing term is added.In this sense,the superfluid breaks aZ2symmetry rather than aU(1) symmetry.Although there is no particle number conservation,there is still a charge gap in the MI phase,and there is no long-range correlation between particle annihilation and particle creation.In this sense,the concepts of the Mott insulator and superfluid are slightly modified,but are still well-defined.

3.Mean field theory and phase diagram

Now we apply a mean field theory to the Hamiltonian equation(1).First,we propose a mean field Hamiltonianas follows,

wherei∈{1,2,3} are sites indices in a unit cell with three sites in it,φ=(φ1,φ2,φ3) are complex order parameters.The addition and subtraction in{1,2,3} are cyclonic,which means 1-1=3,3+1=1.Now we suppose the eigenstate ofis |gφ〉.We take this solution as an ansatz of the original Hamiltonian’s ground state.Then we can obtain the ground state energy as

By minimizing ground state energyEg,then we obtain the mean field solution for φi=1,2,3by equations

To better describe the order parameters,we find a decomposition as follows,

Following the calculations for the order parameters,we can then draw a phase diagram for fixed η/U,varying μ/UandJ/U.The total phase diagram is shown in figure 3(a)and(b).Compared with the phase diagram at η/U=0,there are inhomogeneous density ordered superfluid phases with,or without chiral order.It shows that a density-ordered superfluid is possible under the competition between frustration and the local interactions.

4.Mechanism study

Now,we try to understand the phase transitions and figure out the mechanism.Here η term is taken as a perturbation.Based on equation (7),we find up to the second order of φ,the ground state energyEgcan be expressed as

In region II,let us assume that the superfluid order is large enough that we can neglect the fluctuations of the magnitude mode of φ,then we find the effective ground state energy can be written as [31]

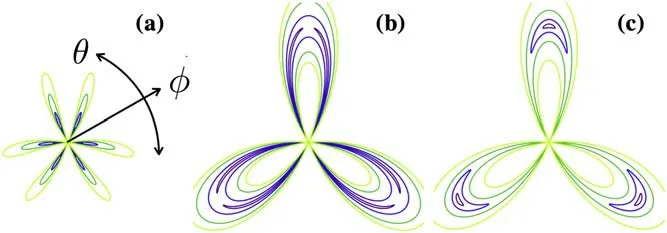
Figure 4.Cross sections of the energy curve for equation (12).For small λ,the typical energy cross section is presented in (a).The minimum is surrounded by the purple curve.We can see the minima are located at ϕ=0,θ=nπ/3,n ∈Z.For large λ,the superfluid phase changes in case.The typical energy cross-section is shown in(c).Here ϕ ＞0,ϕ ≠0 and θ=3π/6,7π/6 and 11π/6.In (b),we have shown the energy cross-section of a λ close to the critical point.We can see there is a purple curve shaped like a shamrock,where the ground state energy is almost degenerate along the purple line.This is the case for emergent U(1) symmetry.

The effective theory given in equation (12) is in the same universality class of the six-state clock model[32–36],and it enables us to have some guesses for finite temperature phases.Ford=2 (dis the spatial dimension),if the system doesn’t have particle-hole symmetry,then the total dimensionDis still 2 (Dis the quantum dimension).Then when the temperature rises,the system first goes through a first-order transition from DWSF to a KT phase with a recovered U(1) symmetry.As the temperature continues to increase,the KT superfluid phase becomes a disordered phase.Although it may not be so surprising from an effective field theory view,the U(1) symmetry here is quite different from the original U(1) symmetry.Under this U(1)symmetry,the density pattern can rotate from (0,1,-1)mode to(2,-1,-1)mode,which seems to be a very exotic non-homogeneous superfluid.If there is particle-hole symmetry,the(∂τθ)2term becomes the leading order in the effective action,therefore the total dimension becomes three.In three-dimensional space,there is only one transition from the ordered phase to disordered phase.Therefore we expect a critical line to start from the quantum critical point which separates superfluid A and superfluid B.

5.Conclusion and outlook

To summarize,we have proved that a DWSF is possible due to the competition between frustrations and local interactions.In the modified Bose–Hubbard model on a triangle lattice,a Mott insulator phase,and four DWSFs are discovered by the meanfield theory.An interesting transition (the shamrock transition)between two non-chiral DWSFs is discovered where an emergent U(1)symmetry is presented at the critical point while both phases on each side have aZ6symmetry.This model can be realized in Kerr cavities or exciton-polariton systems.It is a good platform for density-ordered superfluid studies and KT transition studies.Different from frustrated spin systems,the Higgs modes are unlocked in the present system.It is also a good platform to study Goldstones with light masses.Many new physics are generated due to the unlocked amplitude fluctuations.

Acknowledgments

We would like to thank Shaokai Jian and Shuai Yin for the valuable discussions.Y C and C W are supported by the Beijing Natural Science Foundation (Z180013) (YC),National Natural Science Foundation of China(NSFC)under Grant No.12174358(YC)and No.11734010(YC and CW),and MOST Grant No.2016YFA0301600 (CW).

Appendix A.Effective theory at φ’s second order and η’s first order

The mean field Hamiltonian is

Up to φ's second order and η's first order,the ground state wave function is

More explicitly,|Ψ〉=∏j=1,2,3⊗|Ψ〉jis a product state of each site’s wave function,where

Here φ is short for φj-1+φj+1.With the help of the perturbative ground state wave function,the ground state energy can be expressed as

whereχ±=χ± 2ηχ′.This is the equation (8) in the main text.

Appendix B.The effective theory with real order parameters only

In some parameter regions,the order parameters are not complex.The presence of a complex order means chiral symmetry is broken.Therefore when we restrict ourselves in non-chiral superfluid,we can simplify the effective field theory.

In mean field theory,we assume the on-site Hamiltonian as

Here we assume that the parameters are restricted to a phase where φj=1,2,3are all real.

By inserting equation(B2)and equation(B3)into equation(B5),and we introduce

whereu,m2,λ are all φ dependent parameters.These parameters can be obtained whenrn=1,2,3and φ are given.