An adaptive energy regulation in a memristive map linearized from a circuit with two memristive channels
Feifei Yang ,Ping Zhou and Jun Ma,3,*
1 School of Science,Chongqing University of Posts and Telecommunications,Chongqing 430065,China
2College of Electrical and Information Engineering,Lanzhou University of Technology,Lanzhou 730050,China
3 Department of Physics,Lanzhou University of Technology,Lanzhou 730050,China
Abstract Nonlinear circuits can show multistability when a magnetic flux-dependent memristor(MFDM)or a charge-sensitive memristor (CSM) is incorporated into a one branch circuit,which helps estimate magnetic or electric field effects.In this paper,two different kinds of memristors are incorporated into two branch circuits composed of a capacitor and a nonlinear resistor,thus a memristive circuit with double memristive channels is designed.The circuit equations are presented,and the dynamics in this oscillator with two memristive terms are discussed.Then,the memristive oscillator is converted into a memristive map by applying linear transformation on the sampled time series for the memristive oscillator.The Hamilton energy function for the memristive oscillator is obtained by using the Helmholtz theorem,and it can be mapped from the field energy of the memristive circuit.An energy function for the dual memristive map is suggested by imposing suitable weights on the discrete energy function.The dynamical behaviors of the new memristive map are investigated,and an adaptive law is proposed to regulate the firing mode in the memristive map.This work will provide a theoretical basis and experimental guidance for oscillator-to-map transformation and discrete map energy calculation.
Keywords: Hamilton energy,dual memristive map,adaptive energy regulation
1.Introduction
The conceptional proposal of a memristor[1],the fabrication of a memristor[2] and its potential application have been widely explored in the control of a nonlinear circuit [3–5],neuromorphic computing [6–8],chaotic systems [9–11],and artificial neural networks [12–15].In fact,a memristor can be embedded into a nonlinear circuit to develop a memristive circuit for presenting rich complex dynamical characteristics.For example,Yangetal[16]designed a simple chaotic circuit by coupling a magnetic flux-controlled memristor (MFCM)with two capacitors and an inductor.The memristive circuit has a complex hyperchaotic phenomenon and the parameter range for the chaotic region is large.Douetal[17]proposed an RC bridge oscillatory circuit based on a memristor,and this memristive circuit can result in symmetric coexistence such as single-scroll,asymmetrical single-scroll,symmetric doublescroll and asymmetrical limit–cycle behaviors.Zhouetal[18]developed a new memristive chaotic system for inducing multistability.In addition,memristive functional neuron models [19–21] are obtained by connecting memristors into a simple neural circuit.
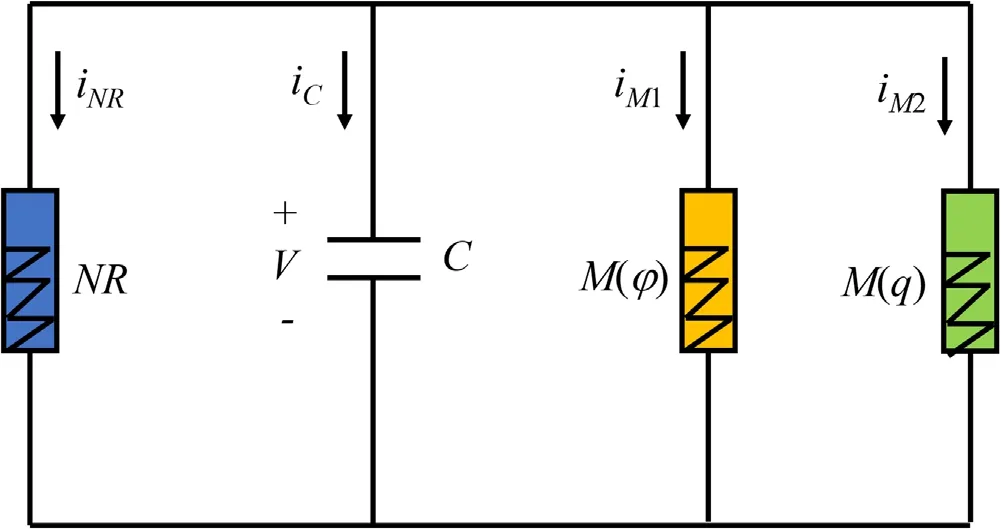
Figure 1.Schematic diagram for a dual memristive circuit.M(φ)denotes mem-conductance for a MFCM and M(q) represents memresistance for a CCM,respectively.C and NR means a capacitor and a nonlinear resistor,respectively.
Recently,discrete memristors (DM) have become a research hotspot.DM's have some advantages such as low power consumption,programmability and anti-interference.Therefore,they have potential applications in the design of DM chaotic/hyperchaotic maps [22–24],neural networks[25–27] and embedded system development [28] fields.Furthermore,a variety of DM maps have been proposed for a dynamical approach and application in signal processing.For instance,Zhangetal[29,30] proposed dual memristor hyperchaotic maps from mathematical assumption.Baoetal[31] designed a parallel bi-memristor hyperchaotic map.The discrete memristive Rulkov neuron map [32,33] was developed by introducing a DM into a Rulkov neuron model.A fractional memristive map is proposed in [34].In addition,DM chaotic maps are hardware implemented by applying DSP platform [35–37] and an analog circuit [38].One important application is that DM chaotic maps are used in image encryption algorithms [39–41].
Most of the previous works about the approach of DM maps suggested that a DM map can be defined by introducing a DM into an existing discrete map.In fact,this kind of description is artificial and is a mathematical assumption without clarifying its inner physical property.The physical modeling of a DM map is not perfect,and the energy of a DM map is also an open problem.Inspired by the suggestion in[42],biophysical and memristive maps can be converted from memristive circuits,in which the energy function for its equivalent memristive oscillator is defined in a theoretical way.In this work,a dual memristive circuit is constructed by using two different memristor elements,a nonlinear resistor and a capacitor.The dual memristive oscillator is derived and its Hamilton energy function is obtained from physical approach.According to the transformation relationship between the oscillator and the map described in [43],the dual memristive map and the corresponding Hamilton energy function are obtained.The results provide further possible guidance for designing discrete maps and calculating their energy.
This study is organized as follows: in section 2,the dual DM map is obtained.The numerical investigations are given in section 3.In section 4,the results are summarised.
2.Model and scheme
Due to the nonlinear properties of the memristor,the dynamics of a nonlinear circuit coupled by the memristor and the memristive circuit become more controllable.In this paper,a memristive circuit is constructed by including a MFCM and a CCM in two additive branch circuits,a nonlinear resistor and a capacitor are coupled in parallel in figure 1.
In figure 1,the current of the nonlinear resistance (NR)can be estimated by
where ρ is the resistance within the linear region,V0denotes a cut-off voltage andrmeans a dimensionless gain.Vis the across voltage of the nonlinear resistor,and the dependence of voltage on the memristive channels current for the MFCM and CCM is defined by
As shown in equation (2),theM(φ) andM(q) have simple forms with low order,and their internal state equations are only composed of linear terms.Compared with higher-order memristors,the memristors in this paper are easier to implement physically.Sinusoidal stimulusAsin(2πωt) is imposed on the memristor,whereAmeans the amplitude of stimulus,and ω denotes the frequency of the stimulus.Thev–icurve for the MFCM with different frequencies ω underA=3 is shown in figure 2(a),thev–icurve for the MFCM with different amplitudesAat ω=0.8 is shown in figure 2(b).
Figure 2 shows that thev–icurve for the MFCM is 8-shaped.The 8-shaped area decreases when the frequency of the stimulus is increased.While the 8-shaped area increases when the amplitude of the stimulus is increased.By applying the same sinusoidal stimulusAsin(2πωt),thei–vcurve for the CCM with different stimuli are displayed in figure 3.

Figure 2.The v–i curve for the MFCM with different stimuli.For (a) A=3;(b) ω=0.8.

Figure 3.The i–v curve for the MFCM with different stimuli.For (a) A=3;(b) ω=0.8.

Figure 4.(a) Bifurcation diagram and (b) the distribution of the LEs for the memristive map by changing parameter a.Setting λ=3.9,b=0.2,c=0.3,d=0.4,β=0.1,δ=0.1.The initial value is (0.1,0.1,0).

Figure 5.Phase portraits of the memristive map by changing parameter a.For(a)a=2;(b)a=1.5;(c)a=1.4;(d)a=0.5.The parameters are λ=3.9,b=0.2,c=0.3,d=0.4,β=0.1,δ=0.1.The initial value is (0.1,0.1,0).

Figure 6.Evolution of energy function and its average value in the memristive map by changing parameter a.For(a)a=2;(b)a=1.5;(c)a=1.4;(d)a=0.5.Setting λ=3.9,b=0.2,c=0.3,d=0.4,β=0.1,δ=0.1.The initial value is(0.1,0.1,0).<Hn>denotes the average value of the Hamilton energy.

Figure 7.Phase portraits of the memristive map by changing initial value v(0).For(a)initial value is(0.1,0.1,0-hπ),(h=0,1,2,3,4);(b)initial value is (0.1,0.1,0+hπ),(h=0,1,2,3,4).The parameters are λ=3.9,a=0.5,b=0.2,c=0.3,d=1,β=0.1,δ=1.

Figure 8.Growth of parameter a,Hamilton energy and phase diagram for gain k.For(a)k=0.005;(b)k=0.007.Setting λ=3.9,b=0.2,c=0.3,d=0.4,β=0.1,δ=0.1.Setting initial values for variables (0.1,0.1,0).
The results in figure 3 confirm that thei–vcurve for the CCM exhibits a similar 8-shaped characteristic.The 8-shaped area becomes larger with the increase of amplitude and frequency of the stimulus.According to Kirchhoff’s laws,the circuit equations for the memristive circuit in figure 1 are described by
To facilitate the analysis,dimensionless parameters and variables in equation (3) are defined as follows
The dynamic equations in equation (3) can be rewritten by
The memristive ciruit in figure 1 has three energy storage elements,the field energyWand its dimensionless Hamilton energyHare given in equation (6).
The Hamilton energy functionHin equation (6) for the memristive oscillator in equation (5) can be proven by applying the Helmholtz’s theorem,when the memristive oscillator in equation (5) is rewritten in a vector form
According to the Helmholtz’s theorem,the Hamilton energy functionHmeets the following criterion
Indeed,the energy functionHin equation (6) satisfies the criterion in equations (8) and (9) completely.Furthermore,linear transformation is imposed on the sampled time series for variables from equation (5) with time step Δτ during a numerical approach.
These renewed discrete variables accompanied with updated parameters can be used to define a new memristive map as follows
Under the same weights for two terms in the discrete energy function for equation(6),the Hamilton energy for the map in equation (11) is described by
As suggested in the recent works [44,45],membrane parameters or memristive parameters can be controlled by the energy flow to induce a mode transition when the inner energy level is beyond a threshold.To investigate the selfadaption in the dual memristive map,it requires that parameterafor the dual memristive map can be controlled by the energy flux in an adaptive way as follows
Where the energy threshold 0 <p<1 determines the energy level of a memristive map in thenth iteration.andenotes value for the map parameter in thenth iteration,parameterkmeans growth step,and the Heaviside function θ(*)is used to control parameter growth to a saturation value.
3.Results and discussion
Similar to most of the memristive oscillators[20,21,46–50],numerical solutions for equation (5) can be obtained and additive noise can be applied to induce nonlinear resonance and mode control in neural activities.Numerical results are mainly explored in the memristive map under the control of adaptive law in equation (13).To investigate the complex dynamic characteristics of the dual memristive map presented in equation (11),the initial values of the memristive map are selected as (0.1,0.1,0).The parameters of the memristive map are fixed as λ=3.9,b=0.2,c=0.3,d=0.4,β=0.1,δ=0.1.The bifurcation diagram and the Lyapunov exponents (LEs) spectrum are calculated by changing the parameteracarefully,and the results are plotted in figure 4.
The results in figure 4 show that the dual memristive map triggers a mode transition with the increase of the parametera,such as period-1,period-2,period-4,period-8 and chaotic behaviors are generated.The positive Lyapunov exponent becomes negative and the inverse double period bifurcation occurs by increasing parameterain a continuous way,and chaos is suppressed effectively.Furthermore,phase portraits of the memristive map with different values for parameteraare shown in figure 5.
In figure 5,the profile of the attractors shows period-2,period-4,period-8 and chaotic characteristics.According to the Hamilton energy function presented in equation (12),the relation between the Hamilton energy and the oscillatory states in the memristive map is calculated,and the results are shown in figure 6.
The results in figure 6 illustrate that the dual memristive map has a higher mean value of Hamilton energy with period state,while it has a lower mean value of Hamilton energy with a chaotic pattern.In addition,the mean value of Hamilton energy decreases with the increase of a period number.
When the parameters in equation (11) are fixed atd=1 and δ=1,the memristive map exits the fixed point (0,0,0±hπ) (h=0,±1,±2,±3…),and indicates that the memristive map can be initially boosted to give extreme multistability.The parameters are λ=3.9,a=0.5,b=0.2,c=0.3,d=1,β=0.1,δ=1,by changing the initial valuev(0),the phase portraits are shown in figure 7.
The results in figure 7 confirm that the memristive map will produce an extreme multistable phenomenon by changing the initial value for the variablev.According to the criterion of the growth for parameterain equation(13),it sets the thresholdp=0.35,parameters are fixed at λ=3.9,b=0.2,c=0.3,d=0.4,β=0.1,δ=0.1,and initial values are selected as (0.1,0.1,0).The initial value for parametera=0.5,gainsk=0.005 andk=0.007,the memristive map in equation (11) is iterated 1200 times,respectively.The growth of parametera,changes of Hamilton energy and phase diagram are shown in figure 8.
It is confirmed that parameteraof the memristive map relative to when the MFCM reaches a stable value of 2.39 after 800 iterations.The Hamilton energy shows a distinct transition when the memristive maps change the chaotic patterns to periodic states,and a similar shift occurs in the phase diagram.By comparing figures 8(a) and (b),it is found that with the increased value of gaink,parameteraneeds fewer iterations to reach a saturation value.The result indicates that the dynamics for the memristive map can be controlled by the energy flow in an adaptive way.Considering that the chaotic systems are extremely sensitive to the parameters and initial values,the map attractor basins ony(0)-v(0) andz(0)-v(0) are shown in figure 9.
It is found that the initial values affect the chaotic region(blue region) and the periodic region (red region) at different initial values.As a result,the stochastic and continuous switch of the initial values for the memristive variables will induce a distinct mode transition and energy shift.
From the memristive oscillator in equation (5) to the memristive map in equation (11),perfect covariance in the formulas is confirmed.The continuous energy function in equation (6) is relative to the state variables and bifurcation parameteradirectly,while the discrete energy function for the map in equation (12) is dependent on the discrete variables and parameterbcompletely.From a dynamical viewpoint,the energy level for both the memristive oscillator and the memristive map can be calculated by adjusting one bifurcation parameter carefully.In fact,the two curves for the energy function in the oscillator and the map seldom intersect,keeping the same energy value due to the involvement of the time step when the memristive oscillator is obtained with numerical solutions.In an experimental approach,analog signals from the nonlinear circuit can be filtered and adjusted to present discrete signals,and the memristive map provides fast computing without further estimating the time step.Our scheme provides a reference to verify the reliability of the mathematical maps.As a result,these physical maps can be connected to build an artificial array for signal processing in parallel.
4.Conclusion
In this paper,a dual memristive circuit is built to develop a memristive oscillator for discerning the effect of the magnetic field and the electric field synchronously.The energy function for the dual memristive oscillator is obtained in a theoretical way.By applying a linear transformation on the sampled variables for the memristive oscillator,a dual memristive map is designed with a clear definition of the energy function and adaptive growth law for one bifurcation parameter.The results indicate that the dual memristive map has rich dynamical behaviors,and the dynamics can be adjusted in an adaptive way under energy flow.The memristive map has a smaller average Hamilton energy value in the chaotic state,while it prefers to keep a higher mean Hamilton energy value in the periodic state.In addition,the mean Hamilton energy value of the memristive map decreases with the increase of the period number.The results confirm the reliability of discrete maps from nonlinear circuits.The modeling method of the discrete map proposed in this paper can be applied to other high-dimensional discrete maps including discrete memristive maps and neurons.The Hamilton energy calculation and adaptive control method can be applied to the energy calculation and the adaptive control of other discrete scatter maps.In addition,the simplest map proposed in this paper can be used for pseudo-random sequence generators and image encryption fields.
Acknowledgments
This study is strongly supported by the National Science Foundation of China under Grant No.12072139.
CRediT authorship contribution statement
FYMethodology,software,numerical calculation,PZandJMMethodology,supervision,formal analysis,writing-final version.
Declaration of competing interest
We declare that all of the authors have no competing financial interests or personal relationships for the work reported in this study.
 Communications in Theoretical Physics2024年3期
Communications in Theoretical Physics2024年3期
- Communications in Theoretical Physics的其它文章
- On the improved dynamics approach in loop quantum black holes
- The electroweak monopole-antimonopole pair in the standard model
- Investigation of proton structure function at HERA in light of an analytical solution to the Balitsky-Kovchegov equation
- An improved effective liquid drop model for cluster radioactivity
- Mott insulator-density ordered superfluid transition and ‘shamrock transition’ in a frustrated triangle lattice
- The multi-impurity system in CdSe nanoplatelets: electronic structure and thermodynamic properties
